基于凯勒方法的微灌双向毛管水力解析模型

韩方军

（新疆农牧区水利规划总站 新疆 乌鲁木齐 830000）

1 引言

实际大田微灌工程中毛管多为双向铺设。微灌双向毛管水力设计的主要任务是：设计最佳支管位置，进口工作压力及评价灌水均匀度。水力解析方法基于经典微灌水力学，可以建立具有明确物理意义的解析模型，应用方便，因此在工程实践中应用广泛。

目前，适用于设计微灌双向毛管的水力解析法可以分为凯勒方法[1]、张国祥方法[2]和蒋树芳方法[3]。其中，凯勒方法定义最佳支管位置位于左右两侧毛管最小压力相等处，可以通过图解法和解析法实现，简单方便，在国际上应用最为广泛。张国祥方法可以满足支管两侧毛管灌水器平均流量等于设计流量，同时可以考虑毛管进口比对设计结果的影响，但该方法需要将毛管水力分布情况进行分级，设计过程较为复杂。蒋树芳方法基于凯勒方法中最佳支管位置的定义，提出了满足允许的最大压力水头和最小压力水头的双向微灌毛管设计方法，可以设计进口工作压力已知的双向微灌毛管。

利用以上水力解析法，可以较好的设计微灌双向毛管的最佳支管位置和进口工作压力，但还缺乏评价整条毛管灌水均匀度的解析模型。本文基于能坡线法，利用数值拟合方法简化凯勒方法，并进一步提出了微灌双向毛管的灌水均匀度评价模型，为提高微灌工程设计效率提供理论依据。

图1 基于凯勒方法的微灌双向毛管最佳支管位置示意图

2 凯勒方法的简化

如图1所示，本文中将双向毛管最佳支管位置定义为逆坡段毛管长度与整条毛管长度的比值：

式中，BMP为双向毛管最佳支管位置设计参数；

Lup为逆坡段毛管长度（m）；

L为双向毛管总长度（m）。

在凯勒方法中，最佳支管位置被定义为使得顺坡和逆坡毛管最小工作压力相等的位置[1]。基于此定义和能量坡度法，构建了双向毛管最佳支管位置解析模型，BMP的解析模型可表示为：

式中，m为流量指数；

J为与双向毛管等长的单向顺坡毛管的坡降比，J=ΔHS/ΔHF；

ΔHS为与双向毛管等长的单向顺坡毛管进口与末端的地形高差，ΔHS=S0L（m）；

S0为地形坡度，S0≥0；

ΔHF为与双向毛管等长的单向毛管的总摩阻损失，ΔHF=FCFsKQm/DbL（m）；

FC为克里斯琴森多口系数，当N＞100时，FC=1/（m+1）；

Fs为考虑灌水器局部水头损失的毛管总水头损失扩大系数，通常Fs=1.10～1.20；

Q为双向毛管进口总流量，Q=N·qd（L/h）；

N为双向微灌毛管灌水器个数，N=L/se+1；

se为灌水器间距（m）；

qd为灌水器设计流量（L/h）；

D为毛管内径（mm）；

K为摩阻系数；

b为管径指数。

设计参数m，K和b取值可查阅《微灌工程设计规范》（GB/T 50485-2009）。

需要明确指出的是，当J＞m+1时，式（2）中BMP无解，此时，微灌毛管仅可以设计为单向顺坡布置，因此，坡降比参数J的取值范围为0≤J≤m+1。查阅流量指数m同时根据已知设计参数得到坡降比J后，可以利用式（2）通过迭代法求解最佳支管位置设计参数BMP，为简化计算，针对不同的流量指数m，通过数值模拟回归了BMP与J的关系式，见表1。

凯勒方法中还构建了双向毛管进口工作压力及灌水器最小工作压力的解析模型，结合式（2），可以简化为：

式中，h0为微灌双向毛管进口工作压力（m）；

hmin为微灌双向毛管灌水器最小工作压力（m）；

hd为灌水器设计工作压力（m）；

α为双向毛管进口工作压力计算参数；

βmin为双向毛管最小工作压力计算参数。

根据式（2），参数α和β均可以表示为坡将比参数J和流量指数m的方程。与BMP类似，针对不同的流量指数m，通过数值模拟分别回归了α和βmin与J的关系式，见表1。

表1中，各回归方程的相关系数R2均大于0.99，说明回归方程具有足够的准确性和可靠性，可以代替原公式进行水力设计。同时，由于回归方程不需要迭代法进行计算，因此可以大大减少计算的工作量，提高设计的效率。

3 双向毛管灌水均匀度解析模型

微灌系统灌水均匀度的评价指标有很多，其中较为常用的有克里斯琴森均匀系数CU，凯勒均匀系数EU，流量偏差率qv和流量偏差系数CV。迄今为止，尚缺乏适用于评价整条微灌双向毛管灌水均匀度的解析模型。本文基于凯勒方法和能坡线法，构建了仅考虑水力偏差影响的凯勒均匀系数EUh和流量偏差率qhv的解析模型。

（1）凯勒均匀系数EUh

仅考虑水力偏差的凯勒均匀系数EUh可表示为：

式中，qminh为仅受水力偏差影响的双向微灌毛管灌水器最小流量（L/h）；

x为灌水器流态指数。

（2）流量偏差率qhv

仅考虑水力偏差的流量偏差率qhv可表示为：

式中，hv为双向微灌毛管压力偏差率，hv=（hmax-hmin）/hd。

其中，hmin可用式（4）求解，hmax为双向微灌毛管灌水器最大工作压力（m），可表示为：

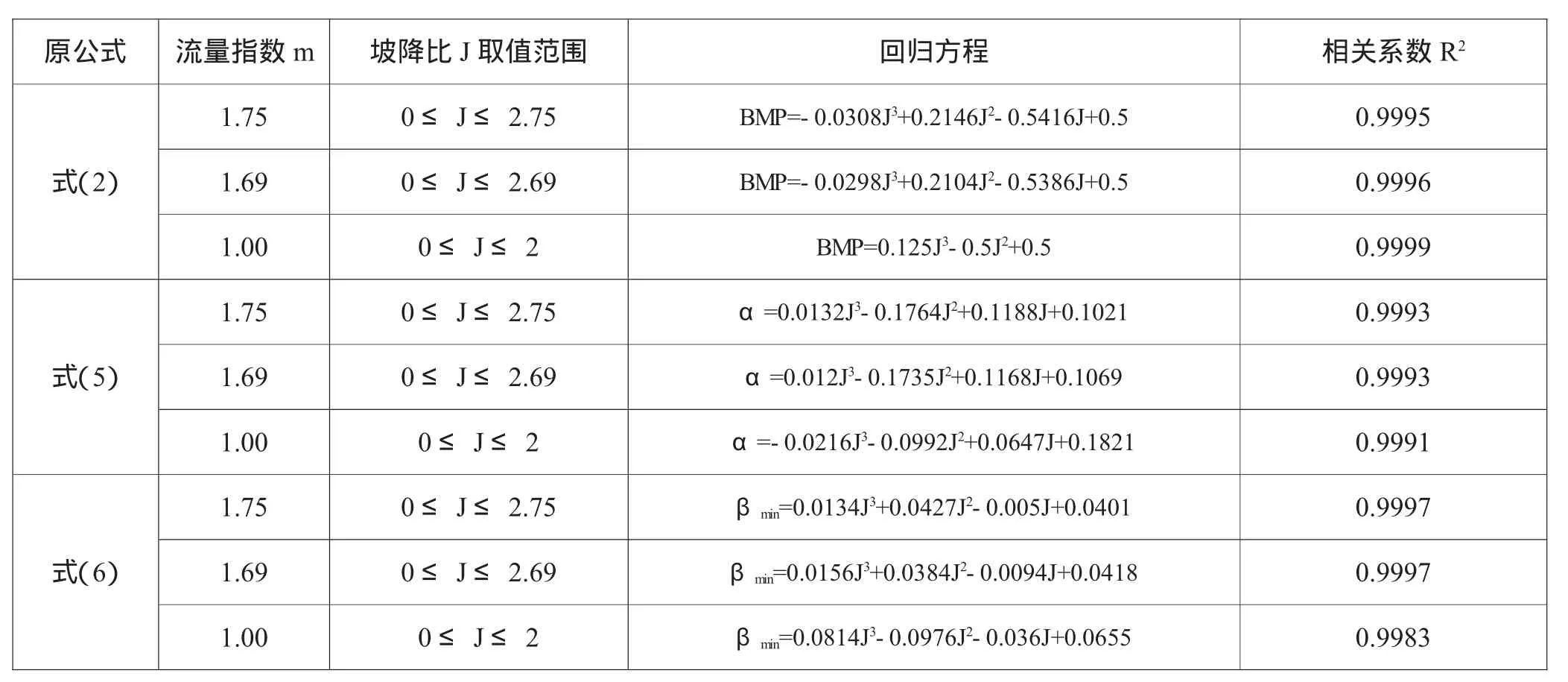
表1 不同流量指数m条件下，双向毛管设计参数BMP，α和βmin的回归方程

式中，Jdown为顺坡段毛管的坡降比，；

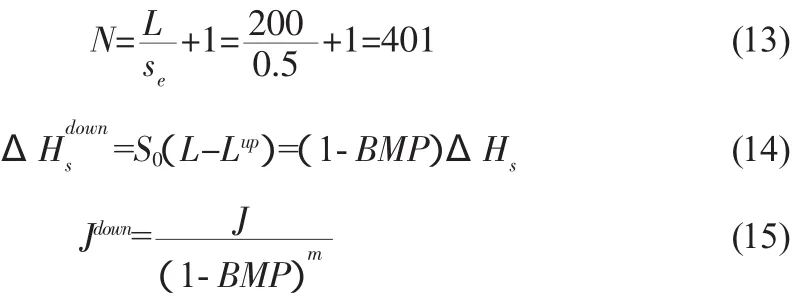
式中，Nup为逆坡段毛管灌水器个数。

将式（11）（12）（13）代入式（10），整理得：

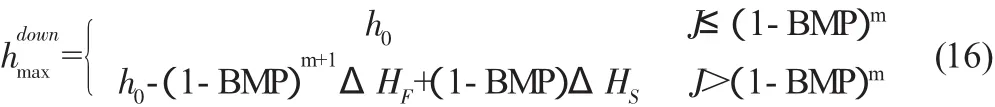
将式（3）（9）（14）代入式（8），整理得：

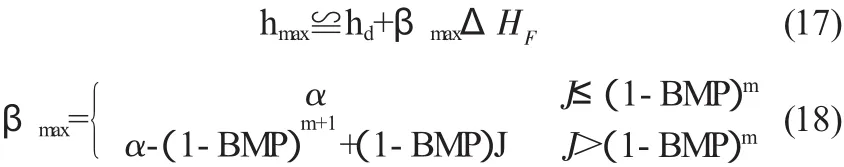
式中，βmax为双向毛管最大工作压力计算参数。

将式（4）（15）（16）代入压力偏差率hv的定义式，结合式（7）整理得：

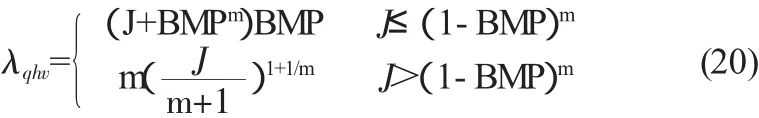
式中，λqhv为双向毛管水力流量偏差率计算参数。

根据式（16）和式（18），βmax和 λqhv均是m与J的分段函数，需要借助于迭代法计算。为简化计算，针对不同的流量指数m，通过数值模拟回归了βmax和λqhv与J的关系式，见表2。

与表1类似，表2中，各回归方程的相关系数R2均大于0.99，证明回归方程具有足够的准确性和可靠性，可以代替原公式进行水力设计，提高工程设计效率。

4 案例分析

已知资料：毛管管径D=15mm，毛管管长L=200m，灌水器间距se=0.5m，支管位于两个灌水器中间，地形坡度S0=0.02，灌水器设计流量qd=1.8L/h，灌水器压力流量关系为q=0.60h0.5。管材水头损失计算系数K=0.505，m=1.75，b=4.75，局部水头损失扩大系数Fs=1.1。设计满足灌水器设计流量的双向微灌毛管最佳支管位置，并计算毛管进口工作压力，灌水器最大和最小工作压力，同时评价灌水均匀度。

为阐述本方法的易用性，此案例的具体设计过程如下：

（1）计算灌水器总个数N

（2）计算双向毛管进口总流量Q

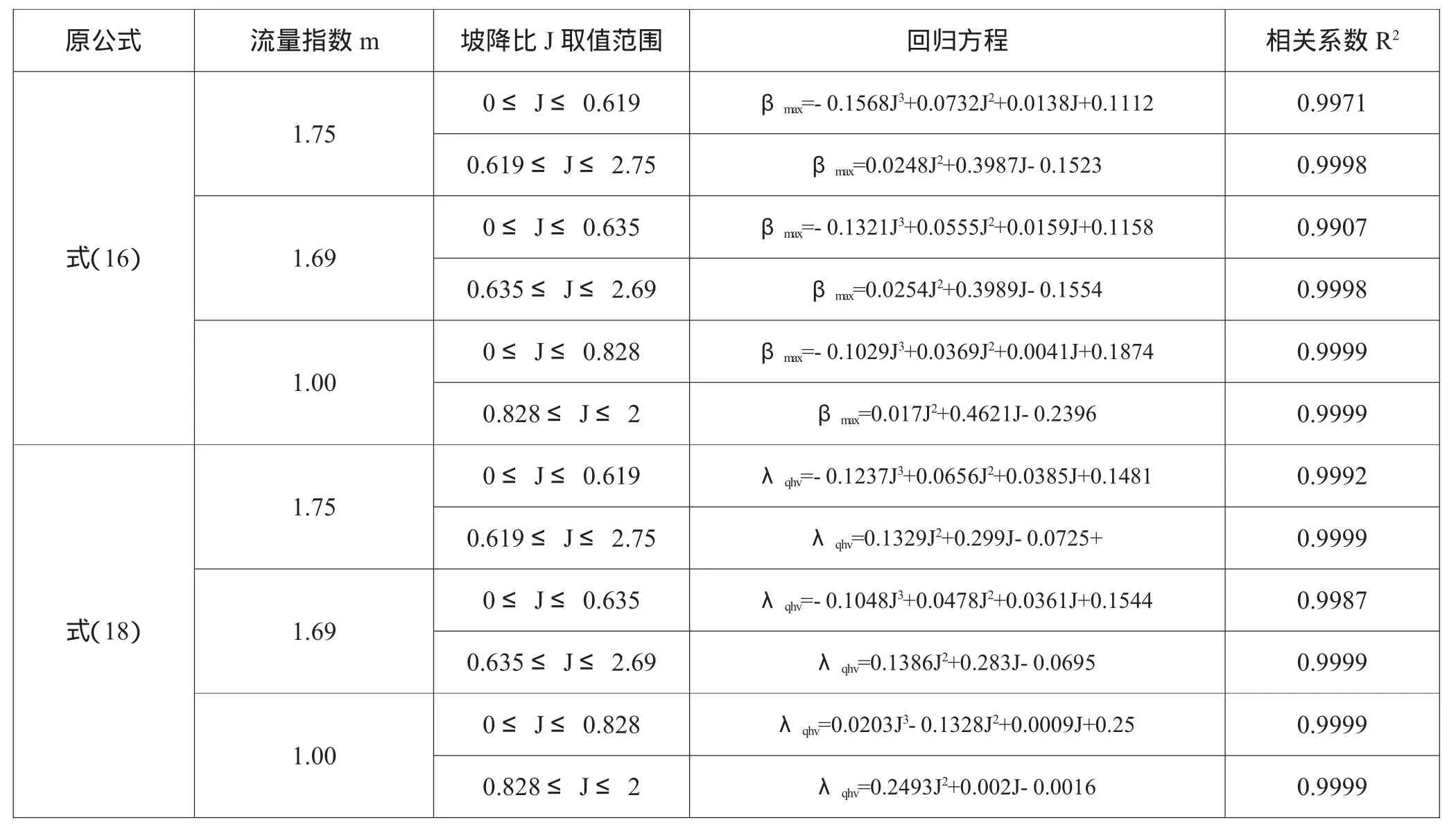
表2 不同流量指数m条件下，双向毛管设计参数βmax和λqhv的回归方程

（3）计算克里斯琴森系数FC

（5）计算与双向毛管等长的单向顺坡毛管进口与末端的地形高差ΔHS

（6）计算与双向毛管等长的单向顺坡毛管的坡降比J

（7）利用式（2）计算最佳支管位置设计参数BMP

（8）计算逆坡段毛管灌水器个数Nup

（9）计算逆坡段毛管长度Lup

（10）计算灌水器工作压力hd

（11）根据J和m的值，利用表1和表2中公式，分别计算双向毛管进口工作压力计算参数α，最大和最小工作压力计算参数βmax和βmin

（12）利用式（3）（15）和（4）分别计算双向毛管进口工作压力h0，最大和最小工作压力hmax，hmin

（13）根据J和m的值，利用表2中公式，计算双向毛管灌水均匀度计算参数λqhv

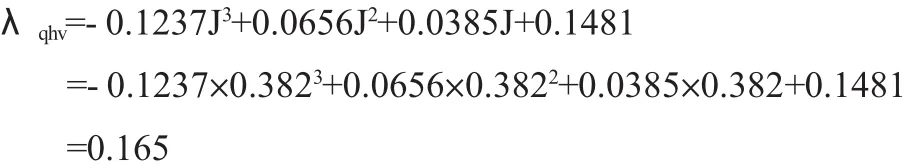
（14）利用式（6）和式（17）分别计算双向毛管灌水均匀度评价指标EUh和qhv

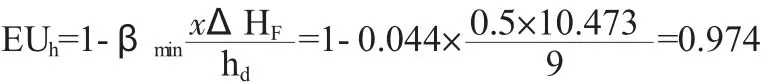
显然，按照上述设计流程，微灌双向毛管的水力设计不需要任何迭代运算，计算简单高效。设计结果显示，毛管进口工作压力为10.28m，灌水器最大和最小工作压力分别为10.24m和8.54m，凯勒均匀系数EUh为0.974，流量偏差率为0.095，灌水均匀度满足微灌工程设计规范（GB/T 50485-2009）[4]中水力流量偏差率不超过0.20的要求。因此，此双向毛管设计合理，可以满足灌溉要求。为进一步显示结果的可靠性，根据设计的支管进口位置及进口工作压力，利用能坡线法绘制了双向毛管上灌水器工作压力和流量分布，如图2所示。

图2 案例中双向毛管灌水器工作压力和流量分布

5 结论

本文基于能坡线法和数值拟合方法，简化了凯勒方法中双向毛管最佳支管位置，毛管进口工作压力及灌水器最小工作压力的解析模型，并进一步提出了凯勒均匀系数和流量偏差率的解析模型。通过实际案例演示了利用本文构建的水力解析模型设计双向微灌毛管的具体过程，结果显示本方法简单高效。利用本文构建的灌水均匀度解析模型，可以设计满足灌水均匀度要求的双向毛管的管径和管长。※

[1]Keller,J.,and Bliesner,R.D.（1990）.Sprinkler and trickle irrigation.Van Nostrand Reinhold,New York.

[2]张国祥.微灌双向有坡毛管情况下支管位置的确定方法[J].农业工程学报，2012，28（21）：98-104.

[3]蒋树芳，康跃虎，曲强.坡地上灌水器流量均等微灌双向毛管设计方法[J].农业机械学报，2011，42（7）：82-85+129.

[4]GB/T 50485-2009，微灌工程技术规范[S].北京：中国计划出版社，2009.

[5]张国祥.微灌毛管水力学设计的经验系数法[J].喷灌技术，1991（1）:4-8.