基于ADINA流固耦合的进水塔自振特性分析
2015-07-25刘建峰
刘建峰
(中国电建集团华东勘测设计研究院有限公司 浙江 杭州 310014)
对于长期位于水下的高耸进水塔结构而言,在地震荷载作用下,库区地面运动会使结构和水体间发生较强的相互作用。以往普遍采用附加质量法模拟库水对结构的动力作用[1],这种做法忽略了结构和水体耦合振动影响,假定结构为刚性。实际上,高耸进水塔结构变形是无法忽视的因素,结构变形引起水体边界的改变,造成结构面动水压力分布改变,反过来会进一步影响结构的变形[2]。随着流固耦合领域的研究工作日益深入,针对水工建筑物中的渡槽、大坝、厂房等结构已经开展了流固耦合方面的研究工作[3-5]。因此,基于流固耦合方法研究高耸进水塔动力特性及抗震性能显得十分必要。本文以大型通用软件ADINA为平台,对进水塔内外水体采用基于势的流体单元进行模拟,应用数值方法将其与塔体结构耦合求解,通过流固耦合截面实现进水塔与水体的相互作用,研究水体对进水塔自振特性的影响,并与附加质量法对比。
1 势流体单元基本理论
进水塔周围及内部水体结构采用基于势的流体单元模拟。其算法采用基于线性的无穷小速度公式。势流体单元可以和结构单元进行耦合,结构的运动使得流体产生沿结构边界法向的相对运动,流体对结构产生额外的压力作用,通过压力波的传递实现势流体与结构的相互耦合、相互作用。
1.1 基本假定
基于势的流体单元有如下假定:①无黏,无漩涡,不能进行热传递;②可微压或者几乎不可压缩;③流体边界有相对很小的位移或没有位移;④实际的流体速度远远小于声速或者可以认为流体不会发生流动。
1.2 势流体边界条件
在使用有限元方法分析流固耦合问题时,要想使数值模型能够真实反映实际的物理现象,必须施加合理的边界条件。在程序中,如果流体区域与结构区域共结点,程序会自动在流体与结构交界处施加流固耦合截面。如果流体区域与结构区域不是共节点设置,需手动指定界面,流固耦合界面将势流体单元和相邻结构单元联系起来。水体表面按照自由边界处理。
2 进水塔流固耦合计算模型
本文建立的进水塔及水体有限元模型如图1、图2所示。计算模型整体坐标系取X轴为水平轴指向下游为正,Y轴为纵坐标轴指向左侧为正,Z轴以竖直向上为正。计算模型考虑了一定范围的基岩基础以模拟截断边界的影响,基础前后、左右边界分别按法向链杆约束,基础底部边界采用全约束。水体结构采用8结点三维势流体单元,局部采用4结点三维势流体单元进行过渡。电站进水塔塔体采用C25混凝土,塔后回填混凝土采用C15混凝土。岩石参数按照Ⅲ类岩体参数取值,弹性模量取下限值10GPa。进水塔内外水体体积模量为2.3GPa,密度为1000kg/m3,计算中材料均按线弹性考虑,阻尼比取为0.05。
地震荷载采用基于相位差谱的人造地震动生成技术,所生成人工地震波其频谱特性和峰值加速度与该工程场地谱吻合较好。人工地震动合成参数为:水平向地震动峰值加速度为ah=0.201g,βmax=2.25,特征周期Tg=0.45s。

图1 流固耦合模型

图2 单独水体模型
3 计算结果分析
3.1 进水塔自振特性分析
计算中对于塔体周围地震动水压力的处理方式除了前述流固耦合法外,还有附加质量法。附加质量模型按与塔接触的水体作为集中质量附加在塔身表面相应节点上。《水工建筑物抗震设计规范》[6]公式(10.1.6)用动力法计算进水塔地震作用效应时,塔内外动水压力可分别作为塔内外表面的附加质量考虑,按下式计算:

mw(h)为水深h处单位高度动水压力附加质量代表值;φm(h)和ηw为附加质量分布系数和形状系数,按规范取值,A为塔体沿高度平均截面与水体交线包络面积;a为塔体垂直地震作用方向的迎水面最大宽度沿高度的平均值。
进水塔由于其特殊的功能作用,塔身独立于上游库区中,其周围除与回填混凝土相接的塔背外皆有水环绕。其受到水的作用较其他水工建筑物尤其明显,所以在研究进水塔的自振特性时必须考虑无水和有不同水位的多种情况。塔周围水位是经常出现较大幅度变化的。因此,为了更深入了解水体对进水塔动力特性的影响,本文选取了空库、半库和满库三种水位工况进行了分析。图3给出了流固耦合和附加质量两种模型在三种水位工况下的前6阶自振频率。

图3 塔体前六阶自振频率
从图中可以看出:(1)在满库水位工况下,流固耦合模型与附加质量模型相差不大,前三阶频率分别相差9%、4%、19%。另外两种模型对应的各阶振型也基本一致。流固耦合考虑了水体的影响,更加贴近真实情况,附加质量法各阶自振频率略低于流固耦合法。
(2)半库水位工况下,流固耦合法各阶频率与附加质量方法相差较大:前三阶频率分别相差18%、21%、31%,两种模型对应各阶振型基本一致。可见在低水位时,附加质量法过于保守,应采用更加贴近实际的流固耦合方法研究进水塔的自振特性。
(3)对比空库、半库水位(按流固耦合结果)和满库水位(按流固耦合结果)三种工况:基频各相差约为15%。3、4阶频率,空库与半库相差依旧在15%上下,而满库则与半库频率相差约为30%。5、6阶频率,半库与满库接近,相差在20%以内,而半库和空库频率相差接近50%。从振型图中可以看出原因,空库、半库、满库三种工况塔体在前2阶的振型是基本一致的。从第3、4阶模态,空库和半库工况振型基本相同,但满库工况的振型已经完全不同(空库、半水位为拦污栅墩相对摆动,而满水位为拦污栅墩多阶振动伴水平扭转)。而第5、6阶模态,半库与满库工况振型接近,而与空库振型区别较大。
以上分析说明,高耸进水塔周围水体不但显著影响塔的自振频率,不同水位工况对塔体振型也有较大影响,尤其在低水位工况下,附加质量法过于保守,在塔体自振特性及地震动响应分析中,应用流固耦合方法考虑周围水体的影响十分必要,且更加符合实际。
3.2 进水塔结构参数敏感性分析
3.2.1 回填混凝土高程对塔体自振特性影响
改变进水塔塔背混凝土回填的高度,分别取高度 H=74m、58m、42m、34m,其他参数不变,研究塔背混凝土回填的合适高度,在尽可能经济的条件下,满足进水塔整体刚度及稳定性要求。图4给出了进水塔前6阶自振频率随塔背混凝土回填高度的变化曲线。由图可以看出随着塔背回填混凝土高度的降低,其自振频率也随之降低。回填土高度由74m下降到58m时,各阶频率变化不大,可见当回填土高度大于58m时,继续增高回填对提高塔体刚度的帮助作用不大。当回填土高度下降到42m时,第一、五、六阶频率下降较多,相对H=74m时,分别下降了13.8%、19.5%、13.7%。当回填土高程降低到34m时,各阶频率均有不同程度的下降,其中一阶频率相对H=74m时下降了22.5%。

图4 回填混凝土不同高度下前六阶频率比较
3.2.2 连接梁面积变化对进水塔自振特性的影响
进水塔在拦污栅墩之间和删墩与塔之间设置了横向和纵向连接梁,以保持塔体结构的整体刚度,分析梁截面积对塔体整体刚度的影响程度以利于设计合适的梁结构尺寸。计算中采取保持梁的高宽比不变,从宽度依次增加0.1m的方法(梁的初始截面积0.8m×1m),计算结构自振特性受梁加粗的影响。图5给出了前六阶自振频率随着连接梁截面变化曲线。由图可见,梁截面积的增加,使塔的前后连接更为紧密,因而自振频率增大。各阶频率随着梁截面的增大均有不同程度增高,但不呈线性变化。其中,第三、四阶升高较多。从0.5m到1.0m,第一阶频率增加了8.3%,第三、四阶分布增加了30.4%、12%。梁的截面积受自重等因素的控制,不能无限制增加,因此,看来通过梁的截面积改变对塔体的刚性的提高不是特别有效果。
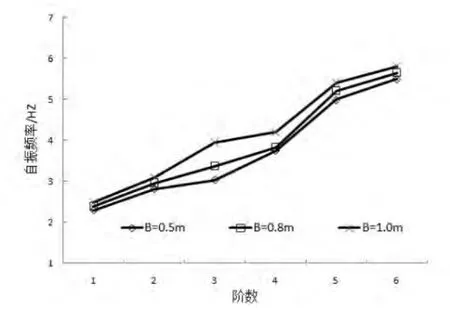
图5 不同梁截面积下前六阶频率比较
4 结论
以实际某水电站进水塔为例,采用ADINA流固耦合分析方法分析了进水塔在各种水位下的自振特性,并与附加质量计算方法进行了比较。进行了塔背混凝土回填高度和连接梁截面积的对塔体自振特性的参数敏感性分析:
(1)低水位下,流固耦合方法与附加质量法相差较大,附加质量法过于保守,高水位下二者相差不多。进水塔周围水体不但显著影响塔的自振频率,不同水位工况对塔体振型也有较大影响:随着水位的升高,塔体的自振频率相应降低,各阶频率降低程度不一,变化程度较大的主要是由于该阶振型发生了明显变化。
(2)塔背回填土高程在58m以下时,自振频率随回填高度变化敏感。连接梁截面积的改变对塔整体的刚度提高作用不明显。陕西水利
[1]求晓明.滩坑水电站分层取水进水塔地震响应计算[J].武汉大学学报(工学版),2010,43(3):302-305.
[2]黄虎,李昇,李建伟.基于流固耦合的高耸进水塔动水压力分布研究[J].水力发电,2012,38(6):30-33.
[3]席仁强,陈国兴,王志华.考虑流固耦合的水中结构物地震反应方法 [J].世界地震工程,2009,25(2):60-67.
[4]CHEN Jiang,ZHANG Shaojie,MIN Xingxin.Fluid-solid Coupling Analysis for Dam-reservoir Interaction [J]. Journal of Southwest University of Scienceand Technology,2009,Vol.24,No.1:13-19.
[5]张存慧,马震岳,周述达,等.大型水电站厂房结构流固耦合分析 [J].水力发电学报,2012,31(6):192-197.
