卫星导航星地实时钟差增量压缩算法研究
2015-07-25谭宏力
宫 磊,马 煦,谭宏力
(北京卫星导航中心,北京 100094)
1 引言
卫星导航系统作为全天候不间断运行的系统,需要对卫星进行实时监测,其中,卫星钟的稳定性对系统服务精度影响巨大。实时测量星地钟差是监测卫星钟性能的重要手段。卫星传送至地面的星地钟差时间序列包含卫星钟差、地面钟差以及卫星钟漂移和地面钟漂移等信息,因此,实时测量的星地钟差数据量很大,需要进行压缩以便于存储和传输。
根据卫星导航系统的接口文件,卫星广播的卫星钟差参数的范围不超过±0.95ms,卫星钟差精确到0.1ns,需要用4字节整型数表示。钟差序列的时标用周计数和周内秒计数表示,需要6字节。这样一个历元的钟差数据包含时标和钟差结果,需要用10个字节表示。按监测频度为1Hz计算,1天的数据量为864K字节。然而这样的钟差序列包含了很多冗余信息,特别是时标信息。由于时标是等间隔的,可以只记录首历元时标,这样有518K字节、约60%的数据量是多余的。对于钟差信息也可以采用首历元加增量的方式表示,进一步压缩数据量。
然而对于实际数据如果出现中断情况,只记录首历元时标,会导致中断后的数据时标错位。如果出现数据跳变情况,计算出的增量会超出数据表示范围,导致数据精度损失。因此,在实际应用增量压缩算法时,首先要分析原始数据特性,对数据中断和跳变情况进行处理。对增量序列进行量化时还要消除累积误差和量化偏差,才能保证压缩后的数据保留原始数据的精度。
2 星地钟差数据特性
星地钟差数据在扣除地面钟差后,包含了卫星钟差和钟差漂移。由于卫星钟差的漂移变化率很小,在短时间内,钟差时间序列可以用1阶线性曲线拟合。1阶线性曲线只需要两个参数表示,等间隔的增量是常数。而实际的钟差时间序列含有观测噪声和钟差波动的信息,等间隔的增量非定常。然而钟差增量是平稳的时间序列,增量变化的幅值是有限的,而原始钟差序列按照线性变化,幅值只受卫星导航系统发播的参数接口限制,变化范围远大于增量变化的幅度。
由于卫星导航系统的接口限制,卫星钟差需要保持在±0.95ms。而卫星钟的钟差漂移在10-10量级,因此每秒钟,卫星钟差的增量约为0.1ns/s。考虑到观测噪声,钟差增量的范围不超过±10ns/s。以0.1ns/s的精度表示钟差增量,只需要1字节即可。
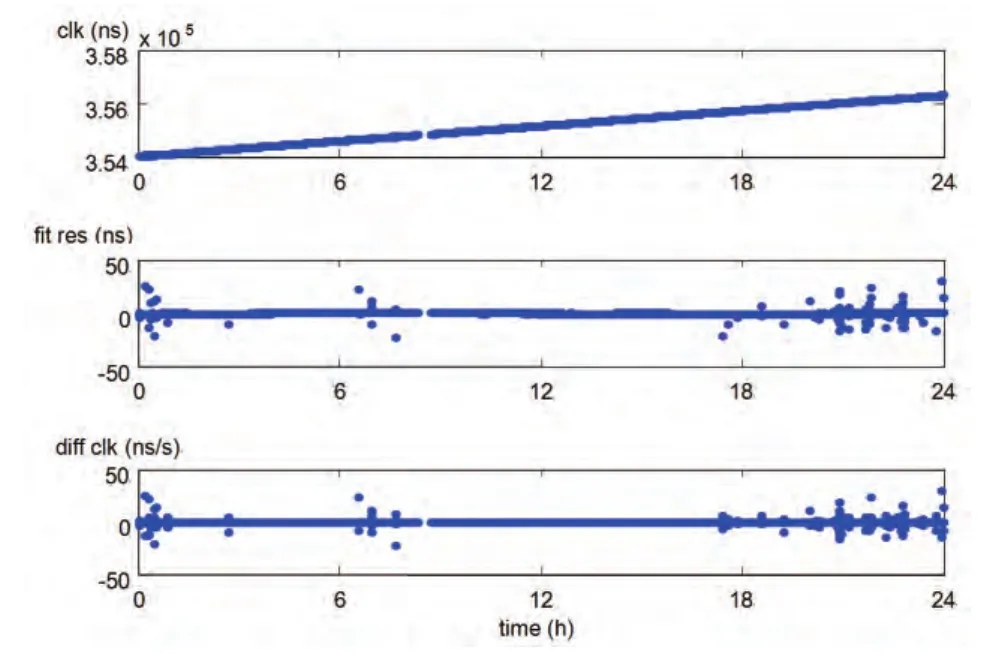
图1 实际星地钟差数据
实际的钟差序列会存在数据跳变和中断情况,图1给出实际星地钟差数据及其1阶拟合残差和增量序列,可以看出在8~9点间数据中断约20分钟,并且存在50ns以内的跳变数据。统计增量序列的均值和方差分别为0.027ns/s,0.34ns/s,变化幅度为52.63ns/s。
3 增量压缩算法
为保证钟差增量变化范围不超过门限和钟差增量序列的连续性,首先要对原始钟差观测数据进行预处理,包括数据跳点剔除和数据间断差值补偿。为保证压缩后的数据保留原始数据的精度,对增量序列进行量化时还要消除累积误差和量化偏差。
3.1 数据跳点剔除
由于钟差增量序列是平稳序列,对增量数据跳点进行剔除可以采用3σ准则予以剔除。首先计算增量序列的均值和方差,然后对每个增量数据点与均值作差,判断差值的绝对值是否小于3倍方差,对于超出3倍方差的数据点打上剔除标记。如果有幅值很大的跳变点,仅作一遍剔除,对小的跳变数据可能无法剔除,因此需要用循环的方式多遍剔除。循环剔除的结束条件可以用剔除前后数据方差的差别小于一定门限为标准。
3.2 数据间断差值补偿
对于数据间断情况可以用差值的方法进行补偿。但如果间断时间过长,对间断数据进行补偿反倒会增加数据冗余,这时可以采用分段方式,把间断过长的数据划分成新的数据段,在每个数据段内部,对间断很短的数据进行差值处理。
3.3 增量数据量化控制
经过跳点剔除和间断补偿的钟差增量数据变成等间隔连续平稳的时间序列,其变化幅度远小于原始的钟差序列,可以用数据位较少的整型数表示。但用整型数表示时会有量化误差,如果直接对增量序列进行量化,会产生累积误差,将增量序列累加还原为钟差序列时,由于量化误差的累积,还原的钟差序列相比原始钟差序列,偏差会越来越大。因此,必须对增量数据的量化误差进行控制。
原始钟差序列记为yk(k=0,1,…,n),量化后的增量序列Δyk,累积的钟差序列为 ,量化因子为p,则
式中,floor(·)为向下取整函数。
由于公式(2)中采用了向下取整函数,计算出的增量序列是有偏的,增量大于0时,累积的钟差值偏小p。因此计算还原钟差序列时,还需要消除量化偏差

式中, 是最终还原的钟差序列,sign(·)为符号函数。
4 实验结果
对图1包含的星地钟差数据应用增量压缩算法,图2的第一幅给出跳点剔除和间断差值补偿后的钟差增量序列,对于中断时间较长的进行了分段处理;图2的第二幅给出还原后钟差序列的量化误差。
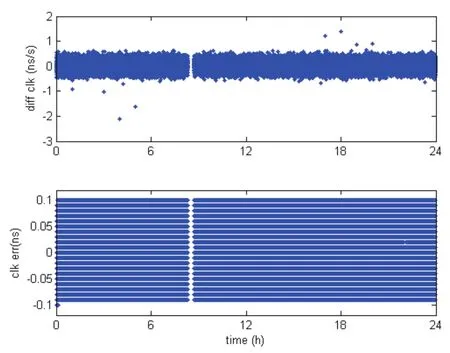
图2 增量序列和还原后的钟差量化误差
由图2的第一幅可以看出,经过跳点剔除和间断补偿后,钟差增量序列的变化幅值小于1ns/s,用p=0.1ns/s的量化因子进行量化,幅值小于100,可以用1字节整型数表示。这样一天的钟差数据(864K)可以压缩到86K,压缩率约为90%。由图2的第二幅可以看出,还原后的钟差精度损失小于0.1ns。
5 结束语
在分析星地钟差数据特点的基础上,本文提出一种增量压缩算法,通过对数据跳点进行剔除和数据间断进行差值,得到等间隔的钟差增量序列,其变化幅度可以控制在有限范围内,相比原始的钟差序列,幅值大大压缩;由于处理后的钟差增量是等间隔的序列,时标信息可以只记录首历元时标,去除大量的冗余时标信息,这样使用增量压缩算法可以对原始数据进行大幅压缩。在对增量数据进行量化时,需要控制增量的累积误差,并对增量的量化偏差进行补偿,可以将还原后的钟差数据精度损失控制在量化因子以内。实验结果表明,增量压缩算法对星地钟差数据的压缩率约有90%,精度损失小于0.1ns。
另外,这种增量压缩算法还可以应用于类似星地钟差数据的线性增长的时间序列,使用时需要分析原始数据增量序列的特性,选择合适的量化因子,控制增量数值的表示范围,可以取得至少60%以上的数据压缩率。■
[1] 赵娜,胡彩波,赵伟,刘春霞.卫星钟及其性能监测与故障处理[J].无线电工程,2012,4: 30-33
[2] 时鑫,刘利,唐桂芬,谭红力.星载原子钟性能评估方法与试验分析[C].上海:第二届中国卫星导航学术年会,2011
[3] 刘志平,郭广礼.精密卫星钟差分形插值算法研究[J].宇航学报,2012,11: 1623-1629
