GNSS信号接收机的研制思考── GNSS导航信号的收发问题之十四

刘基余

（武汉大学测绘学院，武汉 430079）

1 引言

GNSS信号接收机，是一部多种卫星导航信号集成应用的接收设备，广义而言，它是用一台接收机同时接收、跟踪和测量GPS，GLONASS，北斗，Galileo，QZSS，IRNSS等卫星的导航信号，以便在世界上任何地方和任何时侯的陆海空用户，能够精确地测得他们的三维位置、三维速度和时间，甚至三维姿态参数，并确保它们达到稳定可靠的高精度。为了充分发挥GNSS信号接收机的优越性，笔者认为，必须认真解决GNSS信号接收机的下述研制难点。

1.1 GNSS信号接收机的优越性

GNSS信号接收机相对于用单一卫星星座的GPS或GLONASS信号接收机而言，具有下述优越性：

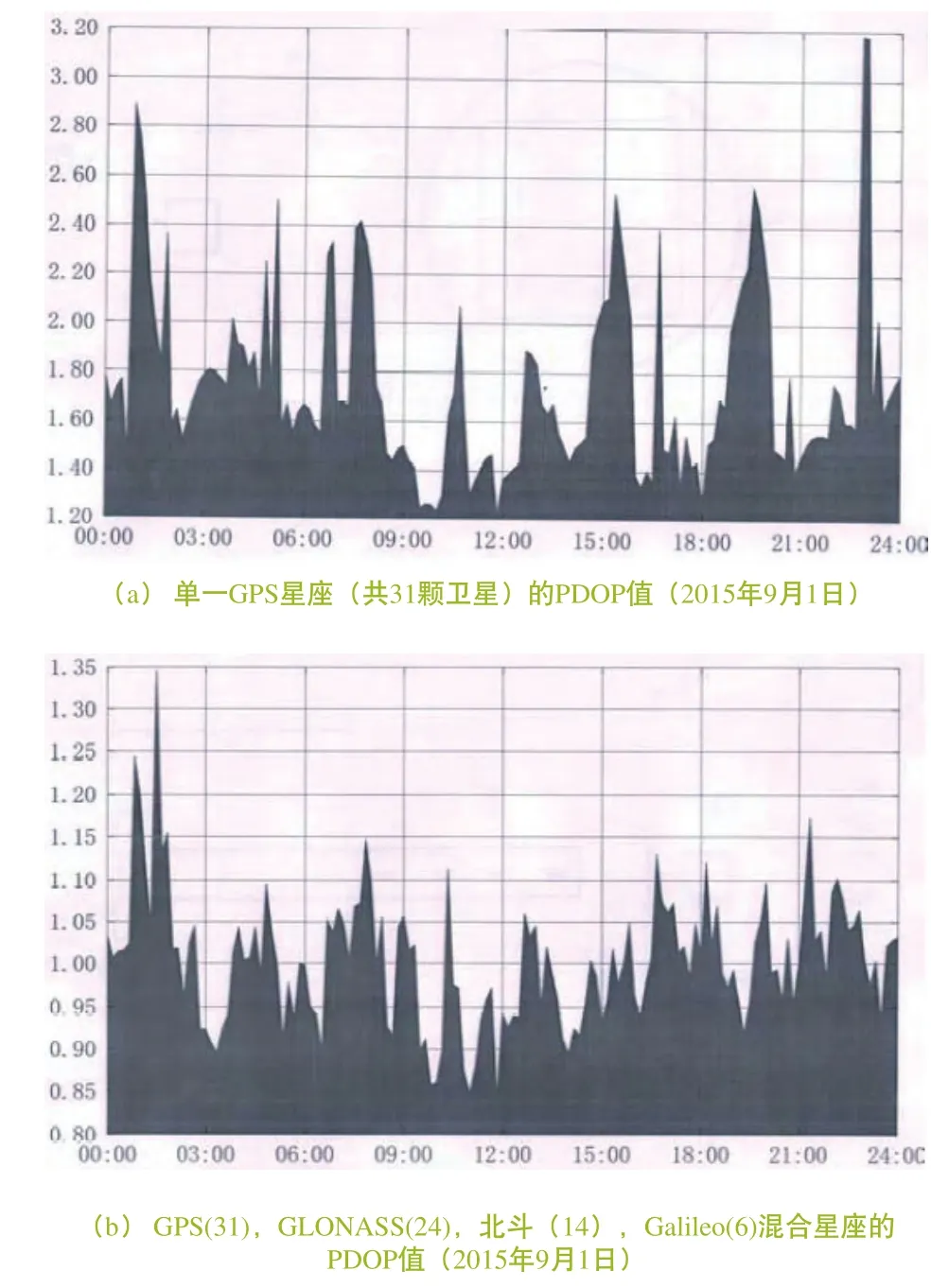
图1 单一GPS星座和GPS，GLONASS，北斗，Galileo混合星座的PDOP值

（1）能够消除间隙时段。当用单一的GPS星座作导航定位测量时，对于某地某时也许只能见到4颗GPS卫星，而这4颗卫星所构成的几何图形又较差，致使它的三维位置几何精度因子（PDOP）超过6，而显著地放大位置和时间误差，这个时段称为“间隙时段”；如果同一台接收机能够同时接收、跟踪、变换和测量GPS，GLONASS，北斗，Galileo等多种卫星的导航信号，则可从几十颗卫星构成的混合星座中选择适宜的卫星，构成定位星座，从而消除上述导航定位测量的间隙时段，以此保证高精度导航定位的连续性和可靠性。图1为2015年9月1日24小时内在武汉地区单一GPS星座（共31颗卫星）和GPS，GLONASS，北斗，Galileo混合星座（共75颗卫星）的PDOP值。从该图可见，单一GPS星座的PDOP最小值为1.23左右，最大值为3.20以上；而GPS，GLONASS，北斗，Galileo混合星座的PDOP最小值为0.85左右，最大值为1.33左右（接近单一GPS星座的PDOP最小值）。因此，从24小时的PDOP值可知，混合星座将使三维位置测量精度提高40%以上。

（2）能够实现真正的全球连续的精确导航。当用单一的GPS星座作导航测量时，理论上只需观测4颗卫星，但试验结果表明，仅仅观测4颗卫星难以实现连续的精确导航，特别是在高动态的应用场合，运动载体和GPS卫星之间存在着较大的加速度径向分量，易于导致接收机跟踪环路的失锁。若采用GPS，GLONASS，北斗，Galileo集成接收机，既可在一天的任何时候接收4颗以上的卫星信号，又可选择径向加速度较小的卫星构成定位星座，而确保精确导航测量的连续性。

（3）能够以较短的数据采集时间获得较高的导航定位精度。例如，仅用GPS/GLONASS集成接收机的试验成果表明，用GPS/GLONASS混合星座作导航定位的二维位置精度比用单一星座的二维位置精度高达70%（如图2所示）；用GPS/GLONASS混合星座作单频差分测量的精度比用单一GPS星座作双频差分测量的精度，是相似的（如图3所示）。

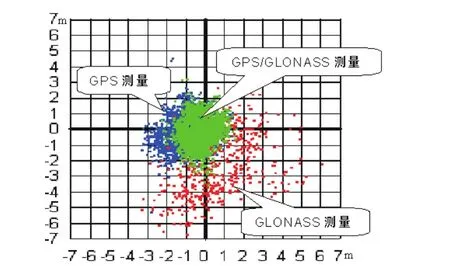
图2 用单一GPS星座和GPS/GLONASS混合星座的二维位置测量精度比较

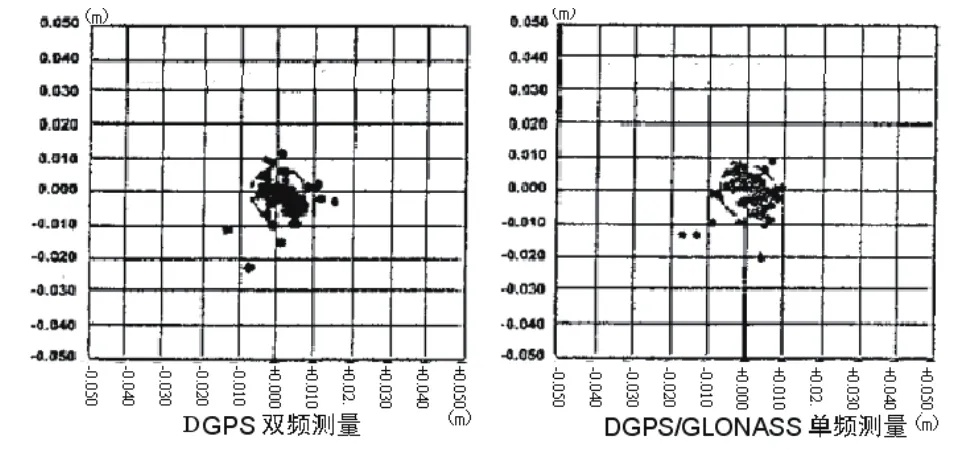
图3 用单一GPS星座和GPS/GLONASS混合星座的二维位置差分测量精度的比较（基线长为3.5km，仅观测10min）

此外，GNSS信号接收机能够在繁杂的地形和地物环境下，甚至在高楼林立的街区进行可靠的导航定位测量，确保用户位置的精确测定。即使某一个星座因故不能为我国用户所用的情况下，而可以采用另几个星座，以此提高利用外国导航卫星的可靠性，而受到我国一些用户的特别关注和重用。

1.2 GNSS信号接收机的研制难点

根据美国“GPS World”期刊于2014年第一期的统计报告可知，受访的47家生产厂商生产了380种GNSS信号接收机，其中，Trimble公司的仅重1.75kg的NetR9 TI-1基准接收机具有440个波道，能够接收GPS，GLONASS，Galileo，北斗，QZSSS，WAAS，EGNOS导航信号，以及OmniSTAR VBS，HP，XP差分改正信号，以致GNSS测距码差分定位的二维位置精度能够达到(25cm+1PPM)，高程测量精度为(50cm+1PPM)；GNSS静态定位的二维位置精度能够达到(3mm+0.1PPM)，高程测量精度为(3.5mm+0.4PPM)。笔者认为，这代表GNSS信号接收机现代的高水平性能。如何使我们研制的GNSS信号接收机达到这种高性能水平？笔者建议采用“细致分析系统间的差异、巧妙处理系统间信号的差别点、选择和使用最佳定位星座”的破解难点之法。

2 细致分析系统间的差异

GPS，GLONASS，Galileo，北斗，QZSS，IRNSS等系统的定位原理都是被动式定位，它们的导航信号也有许多共同点，这对GNSS信号接收机的研制提供了工作基础。但是，细致分析这几系统，它们存在着一些重大差异，值得统筹解决，现予以简要论述。

2.1 导航信号之异

现代的GNSS导航信号，基本上采用三种载波频率，各个载频又调制着多个测距码等信号，此处无法对这几十种导航信号一一予以分析，只能举例说明。

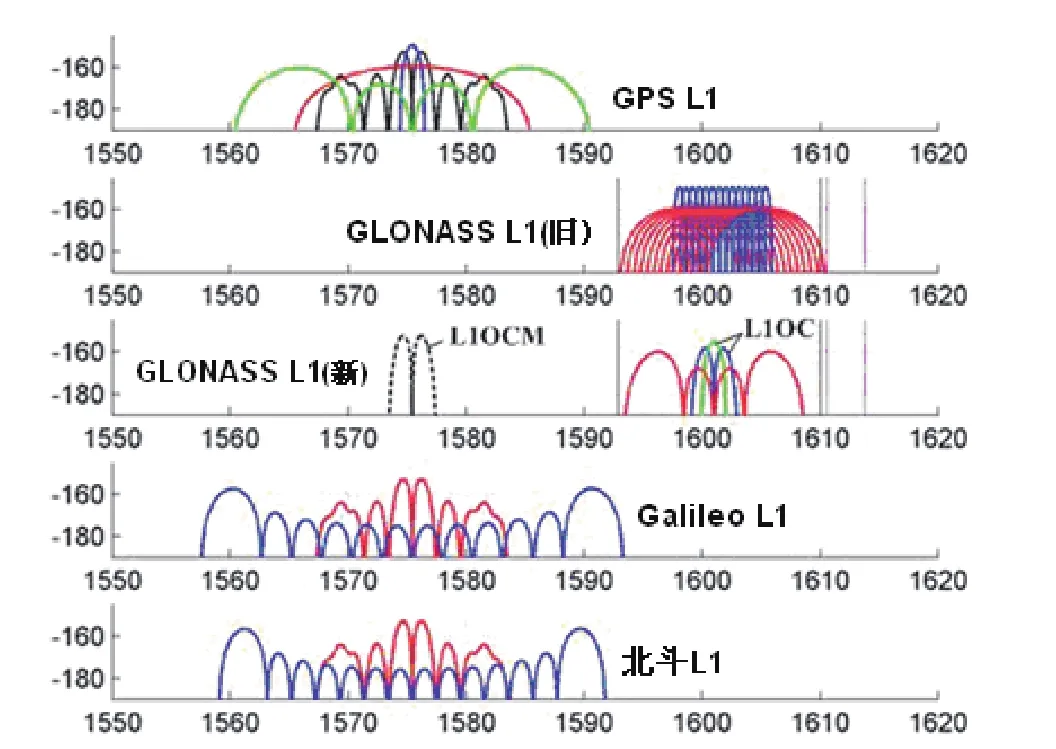
图4A 四大系统的第一导航信号的频谱图

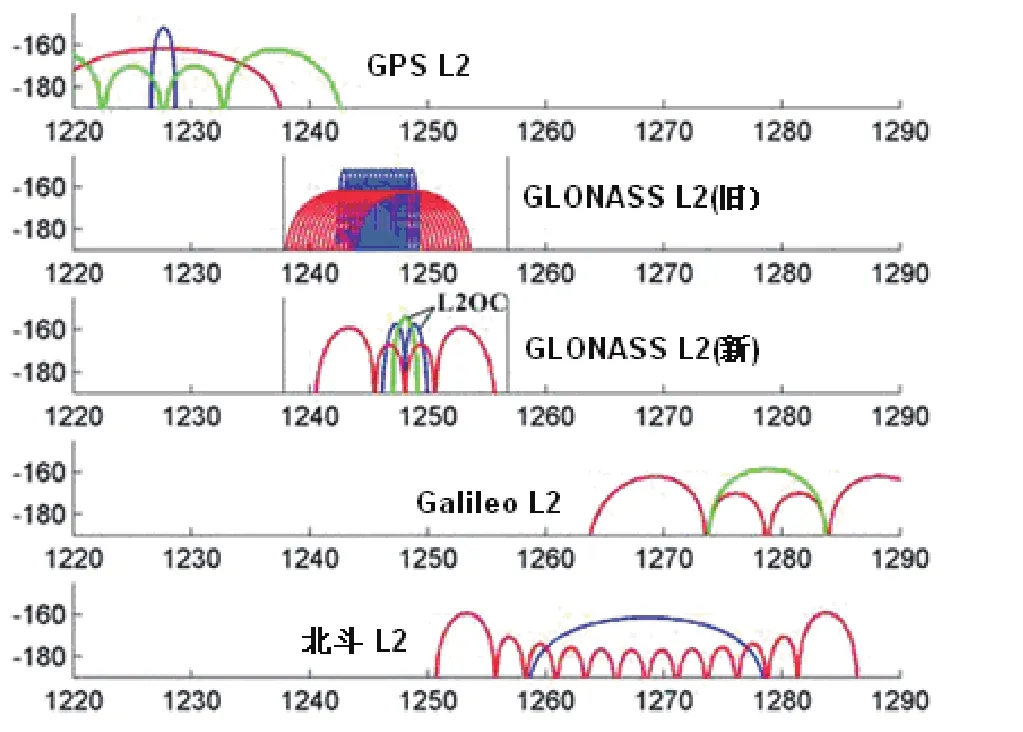
图4B 四大系统的第二导航信号的频谱图

图4C 四大系统的第三导航信号的频谱图4 四大系统的导航信号频谱

Galileo信号和GPS信号虽有许多相近之处，但是，两者却有重大差别。例如，Galileo L1A/B信号和GPS L1信号虽然共用一个载波频率（1575.42MHz），但其信号分量相差较大。仅就调制方法而言，Galileo L1A/B信号分别采用BOC(15, 2.5)和BOC(1, 1)调制，而GPS C/A码和P码均采用BPSK调制，因此，对它们的捕获和跟踪就需要采用相适应的软硬件。BOC信号的自相关函数是一种多个峰值函数，主峰和次峰的幅度差异较小，次峰幅度仅小于主峰幅度30%，从而增加了GNSS信号接收机分辩主次峰值的难度；若将次峰值当作主峰值进行跟踪测量，就会导致较大的测距误差，损失导航定位精度。因此，需要采用不同于捕获与跟踪传统BPSK信号的新技术，以便检测到正确的自相关峰值，实现伪距的精确测量。

GPS，GLONASS，Galileo，北斗系统的三个导航信号的频谱图如图4所示。2011年2月26日发射的GLONASS-K1卫星增设了第三个导航定位信号(L3)，它的载波频率为1201.74～1208.51MHz，并增设了码分多址（CDMA）信号，其载波频率为1202.025MHz，该CDMA信号简称为L3 OC（O为开放使用信号，C为CDMA）。GLONASS-K卫星发送的L3 OC信号，是采用BQPSK调制方式，而且分为数据通道(I)和导频通道(Q)，该信号由1202.025MHz的载波、10.23Mc/s的扩频码和50b/s的导航电文三个部分组成。L3 OC信号是由下述三个步骤生成的：

（1）导航电文编码。数据通道(I)导航电文速率为50b/s，采用标准的（2,1,7）非系统卷积码编码，编码后符号速率为100s/s。导频通道(Q)不包含数据。

（2）扩频码编码。L3 OC的扩频码包括主码和二次编码。主码是长度为10230比特的截短Kasami序列，码元速率是10.23Mc/s，导频通道(Q)和数据通道(I)的初始状态(IS)分别为nIS=62和nIS=30。导频通道和数据通道采用不同的二次编码，导频通道采用10比特的Neuman-Hoffman（纽曼霍夫曼）码（简称为NH码，NH=1111001010），数据通道采用5比特的Baker（巴克）码（BC=11101）；这两个二次编码的字符速率是每个代码字符1ms。

（3）载波的频率为1175×1.023MHz= 1202.025MHz，它用BPSK调制生成L3 OC信号。GLONASS L3 OC信号是一种高精度和高可靠的民用公开服务信号，该信号与GPS L5信号具有相似性，两者的调制方式、电文编码、扩频码和二次编码都有很多相似之处。不过，GPS L5信号需要在2014年才开始由Block III卫星发送给用户。

2.2 时间系统之异

从日常生活到航天发射，从出外步行到航空航海，人们都感受到了时间准确的重要性。GNSS定时，能够为我们提供简便而高精度的定时测量，用户能够以万亿分之一秒的精确度测定时间，而不需要自己拥有高度精确的原子钟。因此，GNSS定时在下列领域获得了广泛应用：通信系统、电力网、金融网和其他重要基础设施的精确同步；无线网络更有效地利用有限的无线电频谱；改善网络的管理及其最优化，使可追踪的金融交易和票据的时间标记成为可能；通过“共视定时”技术使国家实验室之间能够传递高精度的时间；甚至采用GNSS定时作为电视播出系统精确的时间基准，实时地调整系统时钟。

不过，值得我们特别注意的是：各个卫星导航系统所采用的协调世界时，是由所研发国家的天文台测定的，而存在微小差异。例如，GPS的UTC(USNO)与GLONASS的UTC(SU)之间相差±1μs左右；其他卫星导航系统所用的UTC如下：日本QZSS系统用UTC(NICI)；Galileo系统用的UTC，是采用德国UTC(PTB)、英国UTC(NPL)和意大利UTC(IEN)等欧洲国家多个UTC实验室的UTC平均值，记作UTC(K)。我国北斗卫星导航系统的时间系统是北斗时（BDT，Beidou Time），其秒长取为国际单位制SI秒，起算时元为2006年1月1日00时00分00秒协调世界时（UTC），BDT是一种连续时间的时间尺度，通过设在中国科学院国家时间服务中心（NTSC）的标校站作BDT与UTC（NTSC）的时间比对，从而将BDT溯源到UTC（NTSC）。BDT与UTC (NTSC)的偏差保持在100ns以内，BDT的时间系统与GPS时一样无闰秒。BDT与国际原子时（TAI）存在33s的偏差，即BDT+33s=TAI。北斗时与中国军用时频中心（CMTC）的时间进行了比对，得知BDT相对于UTC(CMTC)的偏差小于20ns。需要特别注意的是，目前北斗卫星RDSS导航电文给的时间不是UTC，而是北京时间，它的起算时元为2000年1月1日00时00分00秒（北京时间）！

GNSS卫星时钟改正，是每一颗GNSS卫星的时钟相对于GNSS时系的差值。由于相对论效应，卫星时钟比地面时钟走得快，每秒约差448微微秒（每天相差3.87×10-5s），因此，GNSS卫星的基准频率都需要做相应改正。例如，为了消除相对论效应的影响，GPS卫星将其时钟的10.23MHz之标称频率减小到10.22999999545MHz的实际频率。虽经过了这种改正，但是，还需考虑相对论效应所产生的时间偏移并非常数的问题，对于某一颗给定偏心率e的GPS卫星，一阶相对论效应改正如式（1）所示

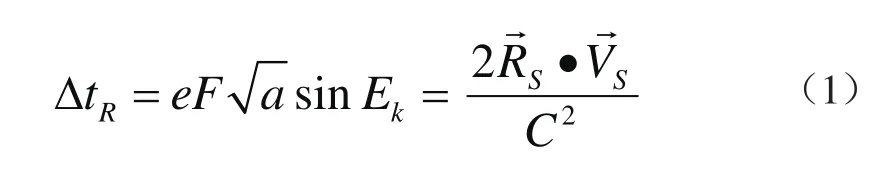
此外，GPS各颗卫星时钟相对于GPS时间系统的偏差误差，也需加以改正，其值为

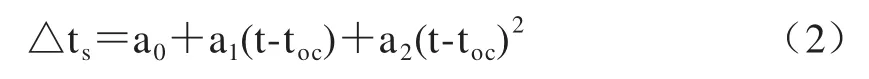
式中，tOC为导航电文第一数据块的参考时刻；a0为相对于GPS时系的时间偏差（钟差）；a1是相对于实际频率的偏差系数（钟速）；a2为时钟频率的漂移系数（钟速变化率，即钟漂），这些系数分别由第9字码和第10字码给出。三个时钟多项式系数a0a1a2总称为时钟参数，且知GPS工作卫星的钟差和钟速最小，铯钟优于铷钟。根据每颗卫星的时钟改正△ts和一阶相对论效应改正△tR，则可将每颗卫星的时间(tS)化算为统一的GPS时间

各颗GPS卫星的GPS时间，还可依据卫星导航电文提供的相关参数，化算成UTC时间。

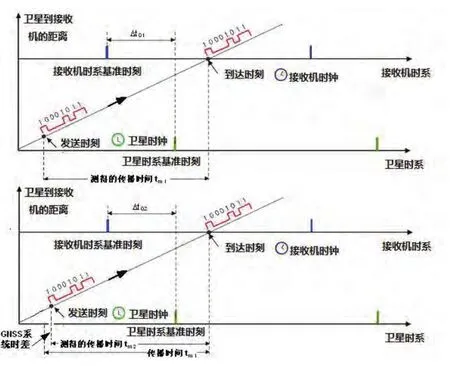
图5 GNSS信号接收机的时间测量图解

由上述GPS时系改正之例可见，GNSS信号接收机在归一化时间系统的时间时，应该首先将各颗GNSS卫星的时间经过各自的卫星时钟改正，进而化算到各自卫星导航系统的UTC时系，然后，还需要对不同的UTC时间做归一化处理，致使GNSS测量成果处于相同的时间系统。图5所示的GNSS信号接收机的时间测量图解表明，仅对两个不同的卫星导航系统（如第1，2个系统）而言，所测得的GNSS信号传播时间就不相同（以tm1和tm2示之），而需要对它们做归一化处理，才能够获得精确值。

从图5可见，GNSS信号接收机所测量的GNSS信号从卫星到达接收机的时间是

式中，△t为GNSS信号从卫星到达接收机的真实传播时间；△t0为卫星时系与接收机时系之间的时间差异。

由式（4）可知，若要精确测得卫星和接收机之间的真实距离（也称为站星距离），除了必须化解时间偏差△t0以外，还需要归一化处理系统间的时间差。值得特别注意的是，±1ns的时间测量误差，将引起±30cm的站星距离测量误差。因此，时间化算是研制GNSS信号接收机的大问题，必须认真予以解决！

2.3 坐标系统之异

1978年2月22日，第一颗GPS试验卫星的入轨运行，开创了以导航卫星为动态已知点的无线电导航定位的新时代。GNSS卫星是环绕地球运行的，它的运行轨道不断地通过地球的质心。为了确切地表述作为动态已知点的导航卫星，必需建立一个以地球质心为原点的大地坐标系。例如，GPS卫星全球定位系统采用WGS-84世界大地坐标系（World Geodetic System,1984），GLONASS全球导航卫星系统采用PZ-90.02地心地固基准坐标系（PZ-90.02 Earth-Centered Earth-Fixed reference frame），北斗卫星导航系统采用2000中国大地坐标系（CGCS2000，也称为2000国家大地坐标系），Galileo全球导航卫星系统采用GTRF大地基准坐标系（Galileo Terrestrial Reference Frame）。由此可见，坐标系是卫星导航系统的重要组成部分之一，没有高精度的坐标基准，就不可能提供高精度的导航定位服务。但是，需要遵循的一定建系原则，致使所建立的坐标系误差对导航卫星星历精度的影响能够忽略不计。对于GNSS信号接收机的研制者而言，应该充分分析它们的差异，予以归一化处理。

北斗卫星导航系统采用2000中国大地坐标系（CGCS 2000，China Geodetic Coordinate System 2000）。它是通过全国GPS一、二级网，国家GPSA、B级网和中国地壳形变监测网的共2,518点经联合平差得到的（平差数据截止至2001年底）。依据GJB6304-2008《2000中国大地测量系统》所述，联合平差分两步进行：第一步，将中国地壳运动观测网络的数据与全球100多个IGS站的数据（H文件形式）进行联合平差，平差中将47个IGS核心站在历元2000.0的ITRF97坐标和速度施以1σ约束，使中国地壳运动观测网络纳入ITRF框架，该网络的平差坐标的平均中误差为σx＝0.070cm，σy＝0.110cm，σz＝0.090cm；水平速度误差为1～4mm/a。第二步，将4个网的单时段基线解进行整体平差。此时，固定IGS站、基准网和基本网的站坐标，给予区域网站的纬度、经度和高度坐标分别给予5mm，5mm，10mm的约束，以保证平差坐标体现的框架对准ITRF97。通过整体平差得到2000国家GPS大地网的坐标精度是：坐标平均中误差σx＝±0.84cm，σy＝±1.82cm，σz＝±1.30cm；σB＝±0.40cm，σL＝±0.52cm，σh＝±2.31cm。位置平均中误差σp＝±2.42cm。基线长度（不计短于20km的基线，平均长度为106km）平均误差0.03×10-6。CGCS 2000是一种右手地固正交坐标系，其原点和轴向的定义是：原点在地球的质量中心；Z轴指向国际地球自转及参照系服务(IERS)参考极(IRP)方向；X轴为IERS参考子午面(IRM)与通过原点且同Z轴正交的赤道面的交线；Y轴与Z，X轴构成右手正交坐标系；CGCS 2000坐标系和GPS系统所用的WGS 84(G1150)坐标系是相容的。计算结果表明，与CGCS 2000椭球体等体积的球半径是6371000.7900m，与CGCS 2000椭球体等面积的球半径为6371007.1809m。

CGCS 2000椭球和WGS-84椭球之异，仅有椭球扁率f有微小差异；椭球扁率之差df(＝fCGCS2000-fWGS-84=1.643484×10-11)将导致同一点位在两个坐标系内的大地坐标产生差异，也导致正常重力产生差异。经过实算数据可知：df不引起大地经度变化；df引起大地纬度的变化范围为0（赤道和两极）至0.105mm（B=45°）；df引起大地高的变化范围为0（赤道）到0.105mm（两极）；df引起椭球面上正常重力的变化范围为0（两极）到0.016×10-8ms-2（赤道）。在当前测量精度水平（坐标测量精度为±1mm，重力测量精度为±1×10-8ms-2）条件下，由于两个坐标系的椭球扁率之差导致同一点在WGS-84坐标系和CGCS 2000坐标系内的坐标变化和重力变化是可以忽略不计的。因此，我们认为，在坐标系的实现精度范围内，CGCS 2000坐标和WGS 84(G1150)坐标是一致的；而且，一般不需要做CGCS 2000坐标和WGS 84(G1150)坐标的变换。

但是，PZ-90.02坐标系与WGS-84坐标系之间，就存在坐标变换问题。因为1982年10月，前苏联发射了第一颗GLONASS卫星时，当时仅有6颗GPS试验卫星在轨运行，苏联人无法利用GPS试验卫星测定大地控制网，而需要独立自主地为GLONASS系统建立地心坐标系，采用了如表1所示的4个不同于WGS-84椭球的椭球基本常数；依据“GLONASS ICD 2008 Edition 5.1”所述，改进的PZ-90.02坐标系仍旧使用表1所示的椭球基本常数，笔者将它称为“PZ-90.02椭球”。现行的在轨GLONASS卫星导航电文均使用PZ-90.02坐标系，故对PZ-90坐标系与WGS-84坐标系之间的差异及其坐标变换问题不予介绍。

经实用研究，PZ-90.02坐标系与WGS-84坐标系和ITRF2000坐标系之间，只存在坐标变换的平移参数，而不存在坐标变换的旋转参数和尺长变化因子。因此，从PZ-90.02坐标（以m单位）变换成WGS-84坐标（以m单位）或者变换成ITRF2000坐标（以m单位）均用下式

从WGS-84坐标（以m单位）变换成PZ-90.02坐标（以m单位）则用

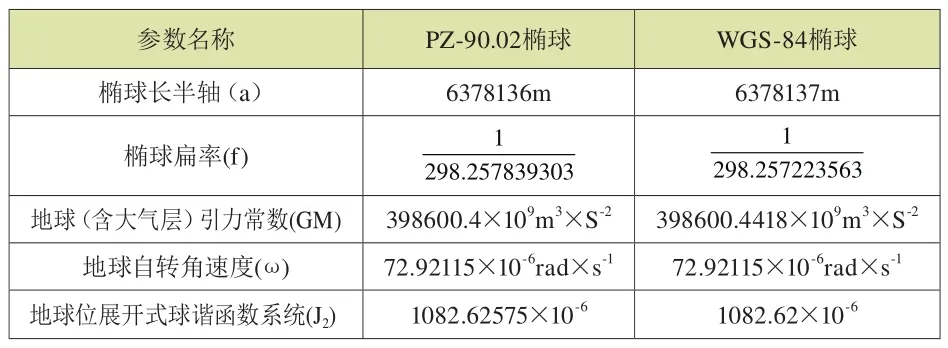
表1 PZ-90.02和WGS-84的椭球基本常数比较

3 巧妙处理系统间信号的差别点

若要求同一台接收机既能接收和测量GPS信号，又能接收和测量GLONASS、北斗、Galileo等导航信号，必须巧妙地处理它们导航定位信号的相异处。从研制接收机的角度看来，首要之举是寻求接收机的公共频率源。现以接收和测量GPS/GLONASS信号为例，予以说明。

所有G P S卫星均有两个相同的载波频率（1575.42MHz和1227.60MHz），而各颗GLONASS卫星载波频率是随着卫星编号不同而异的，且知第j颗GLONASS卫星的两个载波频率分别为

式中，j=1，2，3，…，24；f1=1602.5625MHz；△f1=0.5625MHz；f2=1246.4375MHz；△f2=0.4375MHz。

可见，GPS/GLONASS集成接收机的最基本要求是，必须具有一个联系四种不同载波和四种不同伪噪声码的公共频率源，以便采用GPS/GLONASS混合定位星座（如由3颗GPS卫星和2颗GLONASS卫星构成），共同测定动态用户的七维状态参数（三维位置、三维速度和时间）；也能适宜于采用一种星座作导航定位测量。为此，现在分析两种卫星信号的频率关系。

从式（7）可知，第j号GLONASS卫星的载波频率则为

例如，当j=1时，第1号GLONASS卫星的载波频率分别为

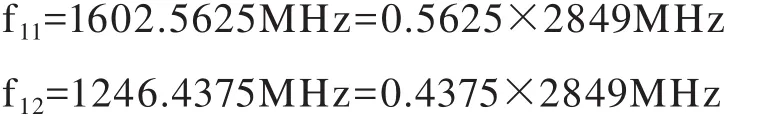
式（8）表明，只要能够获得0.5625MHz和0.4375MHz的信号，便可通过倍频器和分频器获得各颗GLONASS卫星的载波。GLONASS卫星的时钟频率为5.11MHz（其稳定度为3～5E-13）。笔者推论，GLONASS信号的载波频率是用下列倍频和分频方法获得的，例如，第1号GLONASS卫星的载波频率：

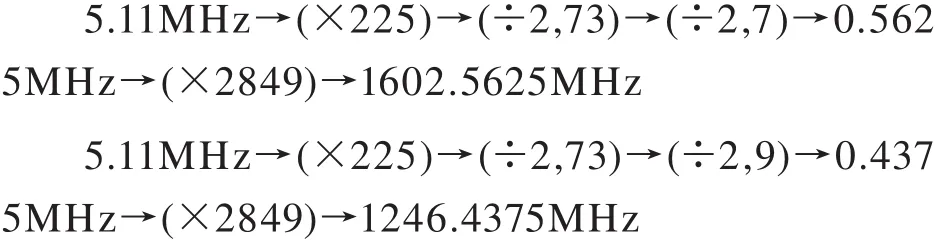
依式（8），按上列倍频和分频步骤，则可从5.11MHz的钟频获得48种载波频率。对于GPS/GLONASS集成接收机而言，若采用5MHz钟频，则可按分频和倍频方法，获得GPS/GLONASS信号的载波频率和伪噪声码的频率。

按上述倍频和分频步骤，并考虑到式（7），即可从5MHz钟频获得48种载波频率。所有的GLONASS卫星，都采用相同的PRN码；而其频率分别为

对于GPS信号而言，两个载波和两个伪噪声码之间具有如表2所示的频率关系，可见，只要从5MHz钟频获得10.23MHz，便可按表2所示频率关系获得各个频率。用5MHz钟频获得10.23MHz的分频和倍频过程如下：

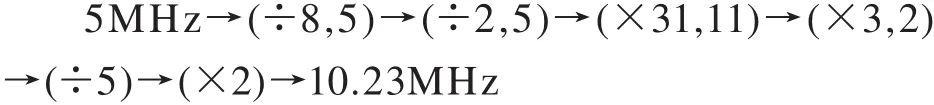
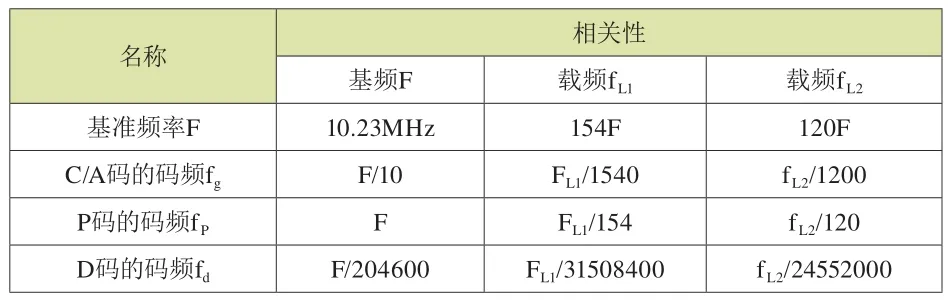
表2 GPS信号的频率关系

综上所述，只要按照上述倍频和分频方法，便可用一个5MHz钟频信号获得GPS和GLONASS信号的近百种频率。一旦GNSS信号接收机选定了中放级数及其中频，便可同机接收和测量许多种卫星导航信号，而实现高精度的导航定位测量，这对GNSS信号接收机的研制是很有效益的。

此外，对GNSS弱信号捕获算法也是值得重视的。就GPS弱信号捕获算法而言，现已研究和实践了非相干累加捕获算法、差分相干累加捕获算法和广义差分相干累加捕获算法。因此，瑞士u-blox公司在一块面积比指甲盖还要小的5mm×6mm×1.1mm的印刷电路板上，集成了一台完整的GPS信号接收机，它能够在GPS信号强度仅为-162dBmW的环境中，实现用户的三维位置定位，即使只能够观测一颗GPS卫星也可以进行精密时间测定。这是值得认真我们研究的。

4 选择和使用最佳定位星座

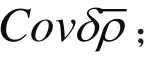
（1）几何精度因子（GDOP）

（2）三维位置几何精度因子（PDOP）

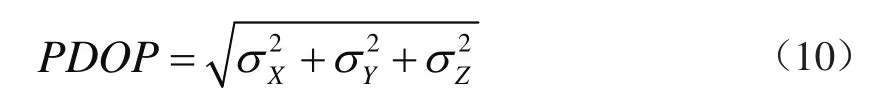
（3）平面位置几何精度因子（HDOP）

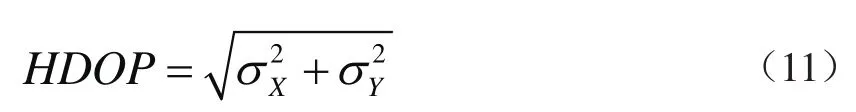
（4）高程几何精度因子（VDOP）

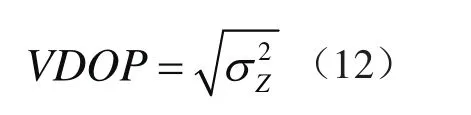
（5）时间几何精度因子（TDOP）

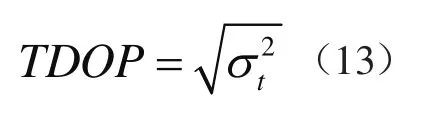
上列各个几何精度因子对用户位置测量精度的损失如式（14）

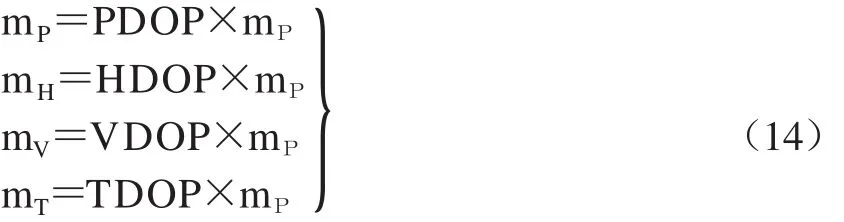
式中，mΡ为用户至GNSS卫星的距离测量误差。

从上列论证可见，GNSS定位星座和用户构成的几何图形越好，GDOP就越小，它对用户位置测定精度的损失就越小。因此，优选GNSS定位星座，是获取高精度导航定位的有效方法之一。研究表明，GDOP与星座四面体的体积成反比（如图6所示），故应选择体积较大的GNSS定位星座与用户构成的多面体，以便获得较小的GDOP值，减少几何精度因子对用户位置测定精度的损失。

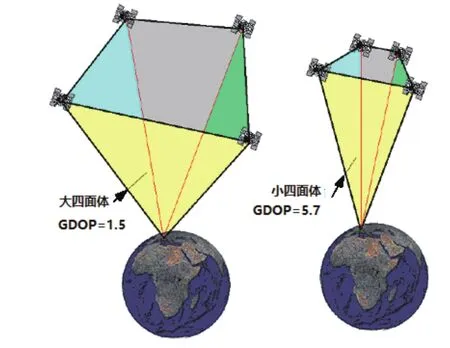
图6 GDOP值随着四面体的大小而变化

2014年的在轨运行导航卫星达到90颗，而到2020年则多达140余颗导航卫星在空飞行。如此之多的导航卫星，用户在任一时元都能够观测到十余颗GNSS卫星。例如，目前能够为用户提供导航定位服务的GPS/GLONASS卫星共达到55颗，任一天的24小时内，能够观测到13～18颗卫星。如果在所研制的GNSS信号接收机中设置定位星座优选软件，能够从这一、二十颗卫星中选举数量适当又能构成最佳定位星座的卫星，进行观测和定位解算，则可获得显著的精度增益，从某种意义说，它比硬件优化设计的效益要高一些。

5 结束语

GNSS信号接收机竞争能力的强弱，主要取决于精度和适应性。广义而论，精度（accuracy）表示一个量的观测值与其真值接近或一致的程度，常以其相应值—— 误差（error）予以表述。对GNSS卫星导航而言，精度直观地概括为用GNSS卫星信号所测定的载体在航点位与载体实际点位之差；对于GNSS卫星测地而言，精度是用GNSS卫星信号所测定的地面点位与其实地点位之差。这为我们提供了鉴定GNSS信号接收机精度的技术途径。

现代的GPS信号接收机，主要包括接收天线、射频前端、数字基带处理器、接收机处理器和导航处理器等部件。它们的作用分别是：捕获在视GPS卫星的导航信号，跟踪它们的运行，测量所需要的导航定位参数，提取卫星导航电文，计算用户7维状态参数。随着微电子技术的迅速发展，常将前一、二两个部件集成为天线模块，而将后三者集成为接收单元模块，再用这两种模块组装成一台接收机。例如，ublox CAM-M80 GNSS天线模块（仅为9.6mm×14.0mm×1.95mm）和UBX-M8030接收单元模块（仅为17.0mm×22.4mm×2.4mm），两者（如图7所示）集成为一台接收机时，能够接收和跟踪GPS，GLONASS，北斗，QZSS，SBAS信号进行导航定位测量。

图7 现代GPS信号接收机的天线/接收单元模块

相对于用单一卫星星座的接收机而言，GNSS信号接收机具有实现真正的全球连续性的高精度导航等一些优点，但是，也需要认真破解GNSS信号接收机的研制难点。为此，笔者仅仅从GNSS系统的研究角度，建议研制者细致分析系统间的差异、巧妙处理系统间信号的差别点、选择和使用最佳定位星座。如果不能够很好地解决各星座之间的差异，特别是时间系统之异，所研制的GNSS信号接收机将不及用单一星座的GPS信号接收机，而实得其反！例如，2014年8月，从互联网上见到一种广泛宣传的由一个“国家北斗重大专项承担单位”研制的“XXXXXX-B1B3GG三模四频卫星导航接收机板”，其性能介绍曰，“该芯片能够达到的精度指标是，水平位置精度为‘BeiDou/GPS:5米（CEP），GLONASS:10米（CEP），BeiDou+GPS+GLONASS:10米（CEP）’；垂直位置精度为‘BeiDou/GPS:10米（CEP），GLONASS:15米（CEP），BeiDou+GPS+GLONASS:15米（CEP）’”。由此可知，该芯片用单一星座（GLONASS）和用三星座（BeiDou+GPS+GLONASS）所得到的三维位置精度是完全相同的！那么，还有必要采用三星座（他们称之为“三模四频”）做导航定位测量吗？仅仅以PD O P值而言，三星座（BeiDou+GPS+GLONASS）的PDOP值也比单一星座（GLONASS）的PDOP值小得多，以致用三星座（BeiDou+GPS+GLONASS）的定位精度要高于用单一星座（GLONASS）的定位精度，绝不可能两者相同。由此可见，本文所论述的破解GNSS信号接收机研制难点之法是值得研制者认真考虑的。

对于星载GNSS信号接收机而言，还需要考虑下述问题：在秒速十来千米的高动态环境条件下，能够稳定地捕获、跟踪和测量在视GNSS卫星所发送的导航信号；具有不低于10Hz的数据更新率，以便获得密度适当的航天器在轨点位；具有1秒脉冲输出功能，以便为航天器上的所有电子设备建立统一的时间标准；在星载GNSS信号接收机内，附设有时元内插器（英文名为Event mark board），以便将航天器上的附属设备作业时元插入GNSS测量数据流。例如，将航天对地摄影时元插入GNSS测量数据流，用于解算出对地摄影时的三维坐标值（称之为摄站坐标），这对我国高分辨率对地观测系统工程的后续发射高分卫星是非常实用的。

此外，BOC调制虽然能够实现GNSS共用相同的载波频率，而有效地分离各自的测距码，互不产生干扰。但是，BOC信号的自相关函数是一种多个峰值函数，主峰和次峰的幅度差异较小，次峰幅度仅小于主峰幅度30%，从而增加了GNSS导航信号接收机分辩主次峰值的难度。即，BOC信号的自相关函数(ACF)不仅具有多峰性，而且随着调制阶数的增加而增加，接收机在捕获BOC信号的同步过程中很容易误锁到它的相关函数边峰上，而产生了模糊性，增加了捕获和跟踪的难度。一旦发生误锁，跟踪环路将产生几十米甚至上百米的测距误差，这对于GNSS信号接收机来说是不能容忍的。因此，需要采用不同于捕获与跟踪传统BPSK信号的新技术，以便检测到正确的自相关峰值，实现伪距的精确测量。这是研制GNSS信号接收机时必须认真解决的重大问题之一。■

[1] 刘基余．全球导航卫星系统及其应用．北京：测绘出版社，2015.5

[2] Terry Moore, GNSS Modernisation and Future Developments Satellite Navigation Nottingham Geospatial Institute, University of Nottingham,March 2012

[3] 刘基余．BOC调制打通共用载频的坦途──GNSS导航信号的收发问题之一．数字通信世界，2013.8.P.38～43