带电粒子在云室中的螺旋线运动探析

2015-07-25邱刚

物理教师 2015年11期

邱刚

（江苏省海门中学，江苏海门 226100）

1 问题的提出

在粒子物理研究中，可让粒子通过施加了匀强磁场的云室使云室中的气体电离来显示出它们的运动轨迹，如图1所示.若有些粒子在云室中运动时的能量减少忽略不计，则可以看到图1中的圆形轨迹，若有的粒子在运动过程中能量降低明显，则速度减小，半径减小，轨迹将呈现图1中的螺旋形曲线［1］.

带电粒子在施加匀强磁场的云室中做螺旋线运动时，若将云室气体对带电粒子的作用力看成是与粒子运动方向相反的气体阻力，同时忽略带电粒子的重力，那么粒子的运动可视为在洛伦兹力和云室气体阻力共同作用下的螺旋线运动.那么带电粒子的螺旋线运动轨迹是何种螺旋线呢？又具有什么样的运动特征呢？在牛顿力学中，我们熟知物体的运动是由受力情况和初速度共同决定的，下面将以此为依据，从力和运动的角度对带电粒子在云室中的螺旋线运动进行探析.

图1 螺旋线曲线

2 螺旋线运动探析

如图2所示，粒子的质量为m，带电量为＋q，粒子进入云室的初速度为v0，取带电粒子在云室中运动平面为xOy平面，以初速度v0的方向为x轴，垂直于v0方向为y轴建立直角坐标系.匀强磁场大小为B，方向垂直于xOy平面向里，这里假设粒子受到与速度方向相反的云室气体阻力f的大小恒定，下面对此种最简单的受力情况下粒子的运动进行分析.

图2 受力情况

2.1 运动特征

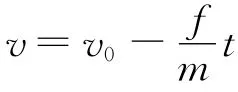
2.2 轨迹方程

粒子在运动过程中的一般位置P的速度方向和受力情况如图2所示，将速度v沿坐标轴分解为

对速度按时间进行积分可得出任意位置P的坐标，即小球运动轨迹的参数方程.

解得

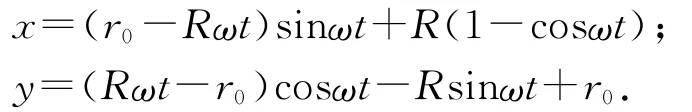
此式为圆的渐开线的参数方程，［2］其中r0为粒子做渐开线运动初始时刻的曲率圆半径，R为渐开线对应的基圆半径，基圆圆心为（R，r0），基圆方程为（x－R）2＋（y－r0）2＝R2.

2.3 渐开线的性质

图3

在几何中可借助圆柱体和细线作出圆的渐开线，如图3所示，将圆柱体垂直固定在一个平面上，在圆柱体的侧面贴近水平面的部位固定一根细线，拉紧细线，让细线绕圆柱在水平面内转动且始终与圆柱相切，那么细线的外端在水平面内的轨迹就是渐开线，该圆柱体的底面称为渐开线的基圆，细线称为渐开线的发生线.从渐开线形成的过程可以看出，渐开线具有以下基本性质：

（1）渐开线上的任一点的速度与细线垂直且细线在转动过程中始终与基圆相切，故渐开线上任意一点处的曲率圆的瞬时半径r就是这一点到基圆切点间的细线长度，曲率圆的瞬时圆心即为细线与基圆的切点.

（2）细线在转动过程中始终垂直于基圆的半径R，那么细线转过多大的角度，切点所对应的基圆半径就转动多大的角度，因此渐开线的瞬时半径转动的角速度等于切点所对应基圆的半径转动的角速度.

（3）细线沿基圆滚过的长度等于基圆上被滚过圆弧的长度，细线长度的变化量等于瞬心在基圆上移动的弧长，跟切点所对应基圆的半径转过的角度成正比，因此渐开线的瞬时半径的变化量跟其转过的角度成正比，如在渐开线上由M到N的过程中，rN＝rM－θR.

2.4 数值模拟

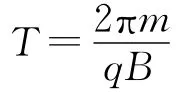
对应的基圆的半径R＝3.6×10－3m，则轨迹方程为

对应基圆的方程为（x－3.6×10－3）2＋（y－0.114）2＝（3.6×10－3）2.

选取10－8s作为时间单位，10－3m作为坐标单位，绘制粒子运动轨迹图的matlab程序如下.

图4

运行程序得到如图4所示图像，形象地呈现了物体做圆的渐开线运动的螺旋线轨迹.

经以上分析可知，粒子在受到与速度方向相反的恒定大小的阻力作用和垂直于速度的方向的与速度成正比的洛伦兹力作用时，粒子的运动轨迹是做圆的渐开线.洛伦兹力与速度成正比关系，可对上述结论进行推广，当物体受到与速度方向相反的恒定大小的阻力作用并同时在垂直于速度的方向受到与速度成正比的线性力作用时，物体做的是圆的渐开线运动.此结论即为物体做圆的渐开线运动的充分条件.