热备用子模块对MMC运行特性影响分析

王朝亮，叶方彬，严华江，吕文韬，童力，赵成勇（．国网浙江省电力公司电力科学研究院，浙江省杭州市 3004；．新能源电力系统国家重点实验室（华北电力大学），北京市 006）

热备用子模块对MMC运行特性影响分析

王朝亮1，叶方彬1，严华江1，吕文韬1，童力1，赵成勇2
（1．国网浙江省电力公司电力科学研究院，浙江省杭州市 310014；2．新能源电力系统国家重点实验室（华北电力大学），北京市 102206）

冗余配置是模块化多电平换流器（MMC）在工程应用的一大技术优点，极大提高了系统的可靠性和可用率。冗余子模块在MMC运行中主要有冷备用和热备用两种状态，热备用子模块参与MMC的运行，会对MMC的运行特性产生影响。引入冗余度的概念，定义了配置有热备用子模块MMC的平均开关函数，基于开关函数法推导出配置有热备用子模块MMC的各电气量的解析表达式，主要研究分析了热备用子模块对于MMC子模块电容电压波动、桥臂环流、频率等稳态运行特性的影响，最后通过仿真进一步验证了理论分析的正确性和有效性。

模块化多电平换流器（MMC）；冗余配置；热备用子模块（SM）；冗余度；开关函数

0　引言

基于模块化多电平换流器转换器的高压直流输电(modularized multilevel converter-HVDC, MMC-HVDC)是电压源换流器型高压直流输电（voltage source converter-HVDC, VSC-HVDC）技术向高电压大功率方向发展的最新成果[1-4]。MMC具有严格的模块化结构和良好的控制特性，适用于高压大功率领域，与传统基于电压源换流器的两电平、三电平VSC-HVDC相比而言，MMC-HVDC有诸多优点：开关频率低，损耗小，采用模块化设计，结构简单，易于扩展，直流母线无需电容器，具有良好的冗余运行能力等等[1-8]。第一个商业化的MMC-HVDC工程“Trans Bay Cable Project (TBC)”于2010年在美国投运，最高运行直流电压为±200kV、输送容量最大400MW，换流器单个桥臂配置有216个子模块[4]。MMC-HVDC技术由于特有的优点日益受到重视，相关技术的研究也成为了学术界和工业界的关注热点。

MMC通过级联大量子模块（Sub-module, SM）来实现高电压，单个桥臂都配有大量子模块，为了避免单个子模块故障造成的系统停运，MMC需要进行冗余设计，配置冗余子模块，提高系统的可靠性及可用率。文献[9]简单介绍了一种MMC的子模块故障冗余保护方案，但是并未对此进行深入地分析和研究，也没有给出具体的实现方法。文献[10]对MMC的子模块故障特性进行了分析，并提出了一种MMC的子模块的冗余保护方法。文献[11]从可靠性的角度提出了一种基于热备用方案的子模块冗余配置计算方法。冗余子模块在MMC运行中主要有冷备用和热备用两种运行状态，冷备用的子模块在MMC稳态运行时不参与工作，对MMC稳态运行特性几乎没有影响，而热备用的子模块在MMC稳态运行时参与工作，会影响到MMC的稳态运行特性。文献[12]将开关函数和瞬时功率理论相结合，建立MMC的时域解析数学模型，该模型给出了换流器桥臂电压电流、桥臂子模块电容电压总和以及单个子模块电容的电压电流的时域解析表达式，可以正确反映上述各电气量与子模块电容值、桥臂电感值及换流器运行状态的关系。文献[13-16]引入平均开关函数，对MMC的稳态特性进行了分析，但都未考虑到热备用子模块的影响，由于热备用子模块参与MMC稳态运行，因此必然对于其稳态运行特性产生影响。目前国内外关于配置热备用子模块的MMC运行特性研究鲜有文献涉及。

本文基于平均开关函数理论，并引入冗余度的概念，计算分析了热备用子模块对于MMC的子模块电容电压波动、桥臂环流、频率等稳态特性的影响，并列写了相应的解析表达式，最后通过仿真试验验证了理论分析的正确性和有效性。

图1　配置热备用子模块的MMC拓扑结构Fig.1 Circuit configuration of MMC with active SM

1　MMC的结构及工作原理

MMC的拓扑结构如图1所示，共有三个相单元即六个桥臂构成。MMC单个桥臂配置有（N+N0）个SM，其中配置有N0个热备用SM（本文暂不考虑冷备用子模块），Udc是MMC的直流电压，L为桥臂电抗器。目前几乎所有的MMCHVDC工程所采用的子模块拓扑结构为半桥结构，如图2中所示，它包括2个IGBT（T1, T2）、2个反向二极管(D1, D2)以及一个直流电容器C0。在正常运行时，T1和T2分别导通，当T1开通时，USM等于电容器电压UC，而当T2开通时，USM等于零。在系统运行时，一旦子模块发生故障，冗余备用的子模块将会替代故障的子模块，避免系统停运，提高系统可靠性。

MMC采用模块化设计，六个桥臂具有对称性，即各子模块的参数和各桥臂电抗值都是相同的。由于MMC的桥臂电压是由桥臂上投入的子模块个数决定的，因此可以将MMC的单个桥臂等效为可控电压源，则三相MMC的等效电路如图3所示。图3中ix（下标x=a,b,c，下同）为交流电流，usx为交流系统输出的相电压，p、n分别代表正负极直流母线，upx、unx分别为上、下桥臂的桥臂电压，ipx、inx分别为上、下桥臂的桥臂电流。

根据基尔霍夫定律并分析图3可得公式（1）和公式（2）。

图2　SM的结构Fig. 2 Structure of SM

图3　三相MMC等效电路Fig.3 Equivalent circuit of three-phase MMC

通过公式（1）和公式（2）分析可知，MMC稳态运行交流侧输出正弦电压波形，直流侧直流电压保持稳定。MMC通过对三个相单元上、下桥臂中处于投入子模块数进行分配实现换流器三相交流电压的正弦输出；通过保持三个相单元中处于投入状态的子模块数在任意时刻都相等且不变，以维持直流电压的稳定输出。

为了对比分析热备用子模块对MMC稳态运行的影响，引入MMC冗余度的概念σ，本文探讨的冗余子模块均为热备用冗余子模块，冗余度也是针对热备用冗余子模块定义的。定义MMC单个桥臂上配置的热备用冗余子模块的个数N0与其稳态运行需要的子模块个数N的比值为MMC热备用子模块的冗余度σ，简称冗余度σ，如公式（3）式所示。

2　平均开关函数的定义

MMC在稳态运行过程中单个桥臂上子模块不断进行投切来实现交流电压波形的输出和直流电压的稳定，最终完成功率的传输，因此子模块的投切与MMC的稳态运行关系密切。为了正确反映出MMC子模块的开关特性，并正确理解MMC桥臂及子模块的电压、电流等电气量的关系， 本文引入开关函数的概念。由前文的分析可知，当子模块投入时，桥臂电流会对子模块电容进行充放电。因此，用开关函数表示SM模块内部的电流和电压值应满足公式（4）。

其中，u0jxp、u0jxn分别为x相上、下桥臂的第j个子模块的电容电压，j=1,2,3…（N+N0）。S0jxp、S0jxn分别代表x相上、下桥臂的第j个子模块的开关函数，当其为1时，相应的子模块处于投入状态，当其为0时，相应的子模块处于切除状态。需要指出的是，根据前文MMC工作原理和阶梯波调制理论，可以认为热备用子模块对于稳态运行的MMC单个桥臂的开关函数之和并没有影响，如公式（5）所示。

o

子模块的开关函数可以表示子模块的开关状态，由于实际工程中MMC桥臂上配置有大量子模块，此情况下子模块的开关函数趋于平均化甚至连续化，用平均开关函数来反映MMC子模块各电气量的状态是工程中比较实用的方式。定义MMC的平均开关函数，未配置热备用MMC的平均开关函数如公式（6）所示，配置有热备用子模块的MMC的平均开关函数如公式（7）所示。

通过文献[15]可知，MMC换流器采用调制波调制时， MMC的平均开关函数用级数形式表示如公式（8）。其中，h为奇数，Dh表示h次谐波幅值的一半， δxh为h次谐波的初相角，ω为系统角频率。

由于实际工程中MMC单个桥臂的子模块数目众多，根据文献[12-15]可知，子模块数目N超过一定量后，公式（8）中的高次量可以忽略，因此MMC的平均开关函数可以由公式（9）表示，m为MMC调制比。

结合公式（3）-公式（9）可知，配置有热备用子模块MMC上、下桥臂的平均开关函数如公式（10）所示。

3　解析分析

为了便于理解和分析，后文的推导基于以下两点前提：一是MMC采用实时触发方式，可以认为控制频率无穷大，子模块可以随时触发；二是MMC所有的子模块在稳态运行前的启动过程中预充电电压都为Udc/N。

通过文献[16]中的分析可知，MMC稳态运行中三相桥臂间存在环流，并且环流中仅含有偶次波成分，其中6k+2次谐波分量呈现负序性质，6k+4次谐波分量呈现正序性质，6k+6次谐波分量呈现零序性质，k=0,2,4,6…。结合图3及前文的分析，MMC相单元上、下桥臂的桥臂电流可以由公式（11）表示。

式中，Ix为x相交流侧电流幅值，θx为x相初相角，Ikf为k次谐波幅值，θkf为桥臂环流各次谐波的初相角。由于MMC内部环流的主要成分是负序性质的二次分量，其他分量所占比重非常小，可以忽略，故MMC相单元上、下桥臂的桥臂电流公式（11）可以简化为公式（12）。

（1）子模块平均电容电流

桥臂电流通过IGBT开关耦合到子模块直流侧，对电容进行充放电，本文把这样流过子模块电容的电流称为电容电流。前文的推导得到了配置有热备用子模块MMC的平均开关函数，则上、下桥臂的子模块平均电容电流可以如下式（13）所示。

其中，

由于MMC稳态运行时交直流侧能量传输守恒，子模块不可能永久充电或放电，因此子模块平均电容电流的直流量必须为零，故i0xp(0)实际上等于0。由公式（13）-公式（17）可知，热备用子模块使MMC子模块平均电容电流幅值减小，并且随着冗余度σ的逐渐增大，平均电容电流幅值不断减小。实际工程中MMC桥臂子模块众多，理论上MMC桥臂子模块足够多时，平均量可以近似表示实际量，公式（13）的推导可以反映热备用子模块对于电容电流幅值的影响。

（2）子模块平均电容电压

子模块电容电流对子模块进行充放电，因此，MMC子模块的电容电压可以通过子模块电容电流求得。结合公式（13），MMC子模块平均电容电压由公式（18）表示，

其中，

K0xp和K0xp为积分常数项，通过初始条件可以求得，因为MMC在启动过程中预充电可以到达其实电压为Udc/N，即电容电压初始值如下公式所示，

将公式（22）带入公式（18），并结合公式（19）到公式（21），可以求得积分常数项K0xp和K0xp，如公式（23）所示，

通过公式（18）到公式（26），联立可以计算得到子模块电容电压的波动如公式（27）所示，

通过公式（27）可知，MMC子模块电容电压波动的幅值由于MMC配置有热备用子模块会减小，并且随着冗余度的增大而减小。

（3）桥臂电压

桥臂电压等于单个桥臂上投入的子模块电容电压之和，在子模块众多的情况下，桥臂电压可以利用子模块平均电容电压求解。将桥臂电压分成基准量和波动量两部分，upx(0)、unx(0)为上、下桥臂电压的基准量，Δupx和Δupx为上、下桥臂电压的波动量，引入平均开关函数，桥臂电压如公式（28）所示。

通过公式（28）-公式（30）可知，桥臂电压基准量不受热备用子模块的影响，但波动量受到热备用子模块想影响，并且随着冗余度的增大，波动量幅值减小。

（4）桥臂二倍环流

热备用子模块有助于减小子模块电容电压波动，理论上子模块电容电压波动的减小有助于减小桥臂环流，因此热备用子模块必然会有利于减小环流。MMC相单元总电压的波动分量可以通过公式（30）计算得到公式（31），

MMC相单元总电压的波动分量仅含有偶次谐波分量，且产生相应频率的环流分量，忽略其高次波成分，可以得到相单元总电压的波动分量的二次谐波分量，并根据公式（2）、公式（28）和公式（31）可以得到公式（32）。

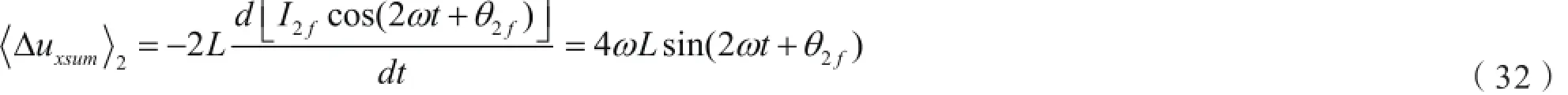
其中，

求解公式（32）可以得到公式（37）和公式（38），

通过公式（37）和公式（38）可知，热备用子模块也会对二倍频环流产生影响，并且二倍频环流的幅值会随着冗余度的增加而减小，但对其相角θ2f几乎没有影响。由于桥臂二倍环流是桥臂环流的主要成分，因此MMC配置热备用子模块有利于降低环流幅值。

（5）开关频率和损耗

由于热备用子模块参与MMC的运行，因此热备用子模块也必然参与投切，目前工程中普遍采用排序均压法，热备用子模块的加入增加了单个桥臂的排序复杂度，同时也使得控制周期缩短，子模块投切任务量加大，子模块的开关频率必然增大。

配置有热备用子模块的MMC在启动过程中子模块预充电要到达电压值Udc/N，故上、下桥臂子模块电容电压之和如公式（39）所示，其都大于直流电压Udc，故在MMC启动过程中单个桥臂所需要储存的能量如公式（40）所示。

由公式（40）可知，配置有热备用子模块的MMC在启动过程子模块预充电耗能较多，并且由于热备用子模块参与MMC的运行，子模块开关频率增加，开关损耗增大[17]，故配置有热备用子模块的MMC的运行损耗会有所增大。

图4　仿真系统主电路Fig. 4 Main circuit of the simulation system

4　仿真验证

为了验证理论解析计算的正确性和有效性，本文在PSCAD/EMTDC环境下建立了如图4所示的21电平双端MMC-HVDC电磁暂态仿真的系统模型。模型单站结构如图1所示，两站结构相同。系统参数设置如下：交流系统电源额定电压为230kV，短路比SCR=20，系统频率为50Hz，换流变压器T1 和T2的容量均为570MW，采用Y0/Δ接法，变比均为230kV/166kV，漏抗LT=0.023H，连接电阻R 为3Ω，整流侧MMC1换流站采用定直流电压和定交流电压控制，额定直流电压为±160kV，逆变侧MMC2换流站采用定有功功率和定无功功率控制，仿真实验中有功传输容量为100MW，无功功率为300MVar，桥臂电抗L0=0.015H，电容C0=0.5mF。

图8　上桥臂电压Fig. 8 The upper arm voltage

为了仿真对比热备用子模块对MMC稳定运行特性的影响，设定两种仿真情形。情形一：MMC单个桥臂上仅有20个子模块，没有配置热备用子模块，冗余度σ为0；情形二：MMC单个桥臂上配置24个子模块，其中4个子模块为热备用子模块，MMC的冗余度σ为20%。两种情形中的MMC系统其他参数都相同。选择以逆变侧MMC2的a相上桥臂为研究对象，其它桥臂可以类推进行分析。

图5　上桥臂子模块平均电容电压Fig. 5 Average capacitor voltage of SM in upper arm

图5为上桥臂子模块平均电容电压波形图，通过两种波形对比可以看出，热备用子模块有助于减小SM电容电压的波动，图5中情形二中的平均电容电压波动的幅值减小到了情形一中的平均电容电压波动幅值的0.8倍，与理论值0.833基本一致，误差主要是因为忽略了桥臂电流和平均开关函数中的高次量。根据子模块电容电压均衡控制理论和目的，理想情况下，桥臂上所有子模块的电容电压波动应该是一致的，因此子模块平均电容电压可以近似反映桥臂上子模块电容电压的波动情况，如图6和图7所示，进一步说明了热备用子模块可以降低子模块的电容电压波动。

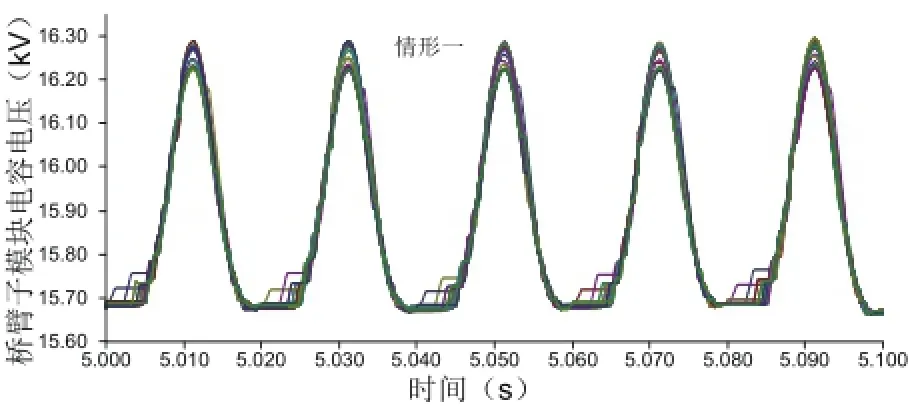
图6　情形一中的MMC上桥臂子模块电容电压Fig. 6 The SM capacitors voltages in upper arm of MMC in case 1

图8是上桥臂电压波形，两种情形的波形基本一致，表明热备用子模块对桥臂电压影响较小。这是因为桥臂电压如公式（28）所示主要由其基准量决定，而热备用子模块仅对占比重较小的波动量有所影响，图8中的局部放大图可以清楚地表现出热备用子模块对桥臂电压波动量的影响。

图7　情形二中的MMC上桥臂子模块电容电压Fig. 7 The SM capacitors voltages in upper arm of MMC in case 2

图9为a相桥臂环流波形图，热备用子模块有助于减小二倍桥臂环流，但其相角θ2f几乎没有受到影响。图10是a相上桥臂电流波形，从图10中可知热备用子模块有助于减小桥臂电流的波动，这是因为桥臂环流的减小导致桥臂电流的波动也减小了。

为了测试子模块开关频率，在系统稳态运行下，本文对a相上桥臂所有的SM的上侧IGBT开关次数在不同情形下进行了统计。根据文献[18]可知，单个器件的平均开关频率fsw_dev可用公式(41)表示，

式中，NK表示单位时间内统计得到的单个桥臂上的所有SM的上侧的IGBT的开关次数（仿真中T1脉冲由0变1记作一次），NX为单个桥臂的SM个数总和。由此可得到表1。表1表明热备用子模块会提高MMC的子模块开关频率。

需要指出的是，限于仿真规模和仿真速度的限制，本文仅仿真了21电平的MMC-HVDC系统，随着电平数的提高，前文的理论解析计算就会越准确。

图9　桥臂环流Fig. 9 The upper arm circulating current

图10　上桥臂电流Fig. 10 The upper arm current

表1　不同情形下的器件的平均开关频率Tab. 1 Average device switching frequency

6　结论

热备用子模块对于MMC稳态运行特性的影响是MMC工程设计急需解决的问题，文中的解析分析在MMC技术的工程应用上具有重要意义。本文引入冗余度的概念，基于平均开关函数理论计算分析了热备用子模块对于稳态运行的MMC的子模块电容电压波动、桥臂环流、频率等的影响，并列写了相应的解析表达式。通过理论分析和仿真验证可以得到以下结论：

1）热备用子模块有助于减小MMC子模块电容电压的波动，并且随着冗余度的增大而减小。但由于热备用子模块仅影响桥臂电压的波动量，因此对桥臂电压影响不大。

2）热备用子模块有助于减小桥臂环流的幅值，并且随着冗余度的增大而减小，但对其相角θ2f几乎没有影响。同时由于桥臂环流的减小，热备用子模块有助于减小桥臂电流的波动。

3）热备用子模块提高了MMC稳态运行的子模块开关频率，也提高了MMC的启动耗能，最终会提高MMC的损耗。

[1] A. Lesnicar，R. Marquardt．An Innovative Modular Multilevel Converter Topology Suitable for a Wide Power Range[C]．Power Tech Conference Proceedings，2003，3：6．

[2] Marquardt R．Modular Multilevel Converter: An universal concept for HVDC-Networks and extended DC-Bus-applications[C]//Power Electronics Conference (IPEC)，2010 International．2010：502-507

[3] Rainer Marquardt．Modular Multilevel Converter Topologies with DC-Short Circuit Current Limitation[C]．Power Electronics and ECCE Asia (ICPE & ECCE)，2011：1425-1431．

[4] 汤广福．基于电压源换流器的高压直流输电技术[M]．北京：中国电力出版社，2009．

[5] 李探，赵成勇，王朝亮，等．用于电网黑启动的MMC-HVDC系统换流站黑启动策略[J]．电力系统自动化，2013，37(9)：117-122．

Li Tan，Zhao Chengyong，Wang Chaoliang，et al． Startup Scheme for Converter Station of MMC-HVDC Using in Grid Black Start [J]．Automation of Electric Power System，2013，37(9)：117-122．

[6] Maryam Saeedifard，Reza Iravani．Dynamic Performance of a Modular Multilevel Back-to-Back HVDC System[J]．IEEE Transactions On Power Delivery，2010，25(4)： 2903-2912

[7] 赵成勇，许建中，李探．全桥型MMC-MTDC直流故障穿越能力分析[J] ．中国科学，2013，43(1)：106-114

ZHAO C Y，XU J Z，Li T．DC Faults ride-through capability analysis of Full-Bridge MMC-MTDC System[J]．Sci China Tech Sci，2013，43 (1)：106-114．

[8] Gum Tae Son，Hee-Jin Lee，Tae Sik Nam etc. ．Design and Control of Multilevel HVDC Converter With Redundant Power Modules for Noninterruptible Energy Transfer[J]．IEEE Transactions On Power Delivery．2012，27 (3)：1611-1619．

[9] 管敏渊，徐政．模块化多电平变流器子模块故障特性和冗余保护 [J]．电力系统自动化．2011，35 (16)：94-98．

GUAN Minyuan，XU Zheng．Redundancy Protection for Sub-module Faults in Modular Multilevel Converter[J]．Automation of Electric Power Systems，2011，35 (16)：94-98．

[10] 胡鹏飞，江道灼，周月宾，等．模块化多电平换流器子模块故障冗余容错控制策略[J]．电力系统自动化，2013，37(15)：66-70

HU Pengfei，JIANG Daozhuo，ZHOU Yuebin et al． Redundancy Fault-tolerated Control Strategy for Sub-module Faults of Modular Multilevel Converters[J]．Automation of Electric Power Systems，2013，37 (15)：66-70．

[11] 王朝亮，赵成勇，许建中．模块化多电平换流器的子模块冗余配置计算方法[J]．电力系统自动化，2013，37(16)：103-107

WANG Chaoliang，ZHAO Chengyong，XU Jianzhong． A Method for Calculating Sub-module Redundancy Configuration in Modular Multilevel Converters[J]．Automation of Electric Power Systems，2013，37 (16)：103-107．

[12] 王姗姗，周孝信，汤广福，等．模块化多电平换流器的数学模型[J]．中国电机工程学报，2011，31(24)：1-8

WANG Shanshan，Zhou Xiaoxin，TANG Guangfu et al．Modeling of Modular Multi-level Voltage Source Converter[J]． Proceedings of the CSEE，2011，31 (24)：1-8．

[13] 宋强，刘文华，李笑倩，等．模块化多电平换流器稳态运行特性的解析分析[J]．电网技术，2012，36(11)：198-204．

SONG Qiang，LIU Wenhua，LI Xiaoqian，et al．An Analytical Method for Analysis on Steady-State Operating Characteristics of Modular Multilevel Converter [J]．Power System Technology，2012 ，36(11)：198-204．

[14] Song Q, Liu W H, Li X Q, et al. A steady-state analysis method for a modular multilevel converter. IEEE T Power Electron，2013，281：3702-3713

[15] 肖晃庆，徐政，薛英林，等．模块化多电平换流器谐波特性解析分析[J]．中国科学，2013，43(1)：106-114

XHAO H Q，XU Z，XUE Y L，et al． Theoretical Analysis of the Harmonic Characteristics of Modular Multilevel Converters [J]．Sci China Tech Sci，2013，43 (11)：1272-1280．

[16] 周月宾，江道灼，郭捷，等．模块化多电平换流器子模块电容电压波动与内部环流分析[J]．中国电机工程学报，2012，32(24)：8-14.

ZHOU Yuebin，JIANG Daozhuo，GUO Jie et al．Analysis of Sub-module Capacitor Voltage Ripples and Circulating Currents in Modular Multilevel Converters [J]．Proceedings of the CSEE，2012，32（24）：8-14.

[17] Steffen Rohner，Steffen Bernet，and Marc Hiller．Modulation, Losses, and Semiconductor Requirements of Modular Multilevel Converters[J]．IEEE Transactions On Industry Applications，2010，57（8）：2633-2642.

[18] 陆翌，王朝亮，彭茂兰，等．一种模块化多电平换流器的子模块优化均压方法[J]．电力系统自动化，2014，38(3)：52-58

LU Yi，WANG Chaoliang，Peng Maolan，et al． An Optimized Method for Balancing Sub-module Voltages in Modular Multilevel Converters[J].Automation of Electric Power Systems，2014，38（3）：52-58.

Analysis of the Influence of Active Redundant Sub-module on Operation Characteristics for MMC

WANG Chao-liang1, YE Fang-bin1,YAN Hua-jiang1, LV Wen-tao1, TONG Li1, ZHAO Cheng-yong2
(1.State Grid Zhejiang Electric Power Research Institute, Hangzhou 310014, China; 2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

Redundant configuration is one of the main technical advantages for modular multilevel converter(MMC) in engineering application, greatly enhancing the reliability and availability of the system. The redundant Sub-Modules in MMC are mainly divided into cold standby state and active standby state, but the active redundant Sub-Module(SM) can participate in the work of MMC and affects the operating of MMC. Introducing the concept of redundancy rate and defining the average switching function of the MMC with active redundant SMs, this paper deduces the analytical expressions for electrical quantities based on the average switching function, demonstrating the effects of active redundant SMs for such performance characteristics in MMC as the capacitor voltage, the circulating current and SM switching frequency and so on. Finally, the results of the analytical expressions coincide with the simulation results, which verify the effectiveness and feasibility of the proposed analysis.

Modular multilevel converter (MMC); Redundancy configuration; Active redundant Sub-Module (SM); Redundancy rate; Switching function

10.3969/j.issn.2095-6649.2015.10.009

WANG Chao-liang, YE Fang-bin,YAN Hua-jiang, et al. Analysis of the Influence of Active Redundant Sub-module on Operation Characteristics for MMC[J]. The Journal of New Industrialization，2015，5（10）: 48-58.

国家高技术研究发展计划（863计划）资助项目（2013AA050105）。

王朝亮(1986-)，男，通信作者，工程师，硕士，主要研究方向为柔性直流输电和FACTS技术；赵成勇(1964-)，男，教授，博士生导师，主要研究方向为柔性直流输电和FACTS技术。

本文引用格式：王朝亮，叶方彬，严华江，等.热备用子模块对MMC运行特性影响分析[J]. 新型工业化，2015，5（10）：48-58.