索-钢/铝合金组合结构初始态确定及静力分析

张莉

(上海大学土木工程系,上海 200072)

索-钢/铝合金组合结构初始态确定及静力分析

张莉

(上海大学土木工程系,上海 200072)

索-钢/铝合金组合结构作为一种新颖的结构形式,是由拉索和压杆(钢管/铝合金圆管)组成的自应力状态下的稳定自平衡体系,体系中受拉连续,受压不连续.在给定结构几何外形和拓扑关系的基础上,采用动力松弛法确定该体系的自应力初始态;在自重及外部荷载作用下,采用牛顿-拉弗森方法分析确定结构的静力性能.为揭示此类结构的受力机理,该体系中的压杆分别采用钢管和铝合金圆管,对比分析两类组合结构在受力性能方面的异同.数值算例表明了本方法的实用性和优越性,为索-钢/铝合金组合结构在实际工程中的推广应用奠定了基础.

索-钢/铝合金组合结构;自应力初始态;力学性能

张拉整体体系是当今国际空间结构领域的前沿研究课题之一,被誉为“未来的结构体系”[1].该体系是一种由拉索和压杆组成的自应力状态下的稳定自平衡体系(以下简称为拉索/压杆体系),体系中不连续受压处于连续受拉的内部.

张拉整体体系所特有的建筑造型、结构形式和力学机理为土木工程师的设计提供了全新的灵感[1].这种体系的潜在优势在于其自成一体,无需强大的下部支承结构,可覆盖如膜、轻型屋面板等轻质屋面材料,从而极具经济性,这就为会展场馆、体育场馆、机场候机楼等大跨度空间结构的设计提供了新思路和新技术.此外,张拉整体体系的应用范围不局限于建筑领域,还可作为艺术雕塑以供观赏,国外学者还将张拉整体的概念扩展到了其他领域如生物学领域中[1-2].

国内外学者的研究工作大多基于张拉整体基本单元或由基本单元拓展而成的张拉整体结构.我国学者对张拉整体体系的研究虽然起步较晚[3],但与国外的研究差距正在逐步缩小.就建筑领域而言,国内外学者的研究成果尚未被应用于大跨度屋盖结构,这方面的工作还有待于进一步研究.

铝合金结构、空间网格结构和索结构在我国逐步得到应用并已颁布相关规范[4-6].本研究在此基础上,将张拉整体体系应用于索-钢/铝合金组合结构,其中的受拉单元采用钢索,受压单元分别采用钢管和铝合金圆管.通过数值方法来确定体系的自应力初始态及荷载态,揭示体系的受力机理,为该体系应用于工程实践奠定理论基础.

1 拉索-压杆体系的自应力初始态确定

自应力初始态确定是指无自重状态下的初始态确定,基于结构给定曲面/平面几何及拓扑关系的力的平衡,不涉及结构本身的材料性能,可采用动力松弛法求解[7-9].

动力松弛法的基本思想是逐点(空间上)、逐步(时间上)跟踪体系的动能,通过递推方程求解.基于牛顿第二定律建立递推方程,通过对时间点上虚拟动态过程的模拟来解决静力问题.首先假定结构的初始曲面或平面几何,可用有限单元来表示,本研究采用拉索/压杆单元.假定结构的虚拟质量M集中在节点上,不平衡节点力激发结构运动,引起节点振荡.节点振荡随着结构动能的逐步减小并趋于零而停止,此时可看作结构处于静力平衡状态.

t时刻空间任一点i在x方向的运动可直接由牛顿第二定律得到,以中心差分形式表示如下:

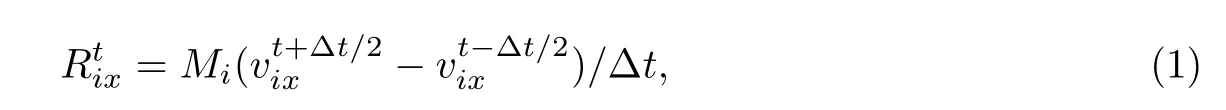
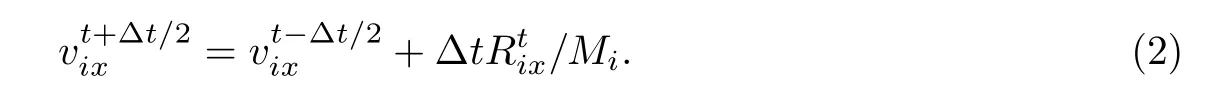
根据Barnes[7]给出的保证解收敛条件,取∆t=1,得到

式中,Simax为节点i的最大可能刚度.对于拉索/压杆单元,节点最大刚度Simax可由下式求得:

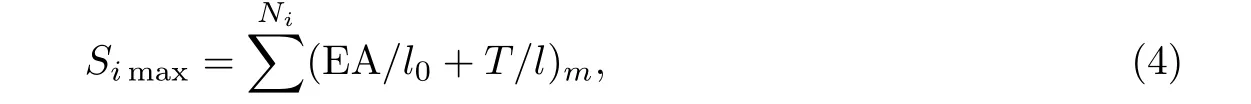
式中,Ni表示交汇于节点i的单元总数,EA为给定的单元轴向刚度,l0为单元m的无应力长度,l和T分别为单元m当前时刻的长度及内力.将式(3)代入(2)得到

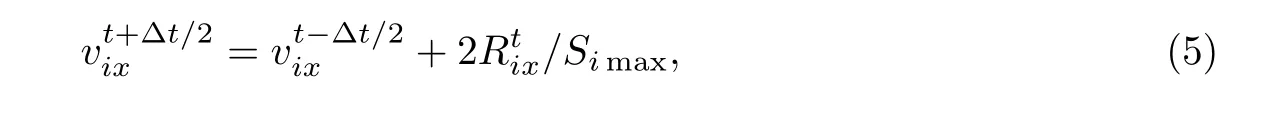
则t+∆t时刻i节点的x坐标变为

根据新的节点坐标可求出各单元内力如下:

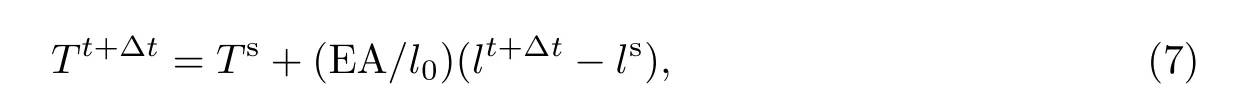
式中,Ts,ls分别为单元初始给定内力和长度.t+∆t时刻节点不平衡力可由下式给出:

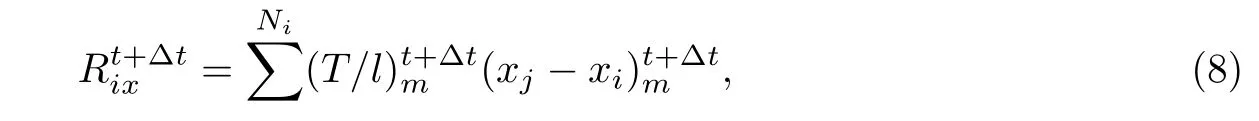
式中,与节点i相连的单元m的另一端为节点j.

计算步骤如下:

(1)假定体系的初始平面或曲面几何及各单元的初始内力,通常情况下假定的内力分布不满足节点平衡条件,此外将节点速度及结构动能设置为0;

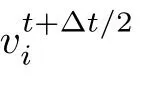
(5)重复步骤(2)∼(4),直到节点不平衡力最大值满足给定精度ε.每次迭代均需记录结构动能E,若下一时刻的动能Et+∆t/2小于前一时刻的动能Et−∆t/2,则体系的动能在t−∆t/2时刻达到极大值,此时将所有的速度分量设置为零,运动从t−∆t/2时刻重新开始.

2 拉索/压杆体系荷载态的确定

荷载态的确定包含两个阶段的设计:第一阶段仅考虑包含体系自重的荷载态确定,以下简称为第一荷载态;第二阶段则在此基础上,考虑外部荷载作用,以下简称为第二荷载态.

2.1 第一荷载态的确定

根据所确定的初始态,按照结构实际所采用的拉索、压杆截面尺寸,求解体系在自重作用下的第一荷载态.考虑几何非线性,可采用牛顿-拉弗森方法迭代求解非线性方程组[8,10],按i=1,2,3,…进行求解:

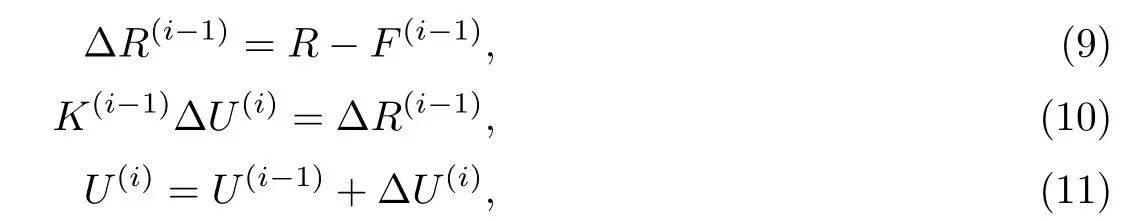
其中

式(9)∼(11)中,R为作用于节点的外荷载,F(i−1)为等价于单元应力的第i−1次迭代的节点力向量,∆R(i−1)为第i−1次迭代的不平衡荷载向量,K(i−1)为第i−1次迭代的切线刚度矩阵,∆U(i)为第i次位移增量修正值,U(i)为第i次迭代的位移向量.

非线性方程(10)的求解还需考虑支座的约束条件,由于拉索/压杆体系为稳定的自应力体系,因此对于各支座节点可仅考虑由自重引起的竖向约束.

对于拉索/压杆单元,轴力T可由下式求得:

式中,l0为单元的初始放样长度,l为当前位置单元长度,EA为单元的实际轴向刚度.单元切线刚度矩阵[kT]为6×6矩阵:

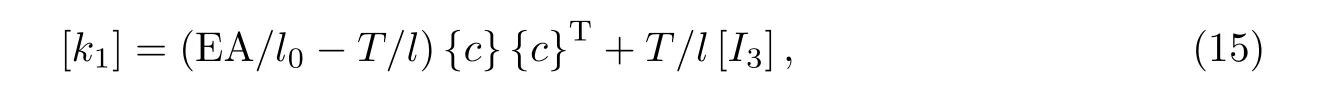
式中,[I3]为3×3单位矩阵,{c}为当前位置的单元方向余弦,可表示为

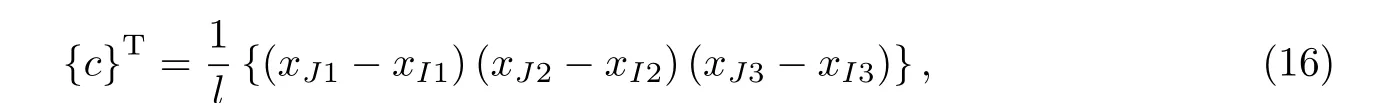
其中I,J为单元的两端节点编号,xI1,xI2,xI3为节点I的空间位置三维坐标.

一个有效的以迭代法为基础的增量解法,必须为终止迭代而采用现实可行的准则. Bathe[10]给出了3种常用的收敛准则.

(1)位移准则:

式中,εD为预定位移收敛限值,表示第i步位移增量的2范数在总位移向量的2范数的预定限值之内.

(2)残余力准则:

式中,εF为预定残余力限值,表示残余力向量的2范数在荷载向量的2范数的预定限值之内. (3)能量准则:

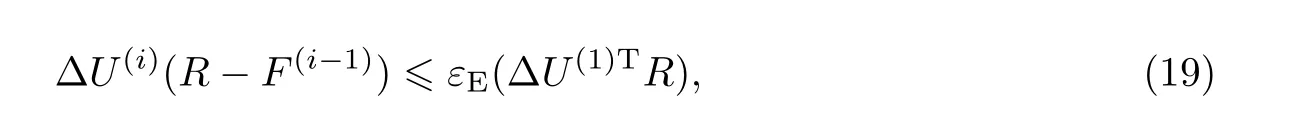
式中,εE为预定能量限值,表示每次迭代时内能增量(即在位移增量上不平衡荷载所做功的大小)的2范数在初始内能增量的2范数的预定限值之内.

2.2 第二荷载态的确定

在仅考虑体系自重的第一荷载态已确定的基础上,考虑外部荷载作用,采用牛顿-拉弗森法迭代求解,此时支座的约束条件依照结构的实际支座约束而定.

3 应用算例

作为理论应用,本研究给出一个数值算例.图1为依据莫特罗[1]给出的“微型网格”所设计的平板型双层拉索/压杆体系,图中以较粗实线表示压杆,以较细实线表示拉索.拉索在上、下层及层间均有布置,受拉连续;压杆仅在层间有布置,受压不连续.鉴于该体系双轴对称,图中仅给出了1/4网格的节点编号.与“微型网格”相比,图1所示体系增加了上层索2-4,1-3和下层索8-11,7-9.

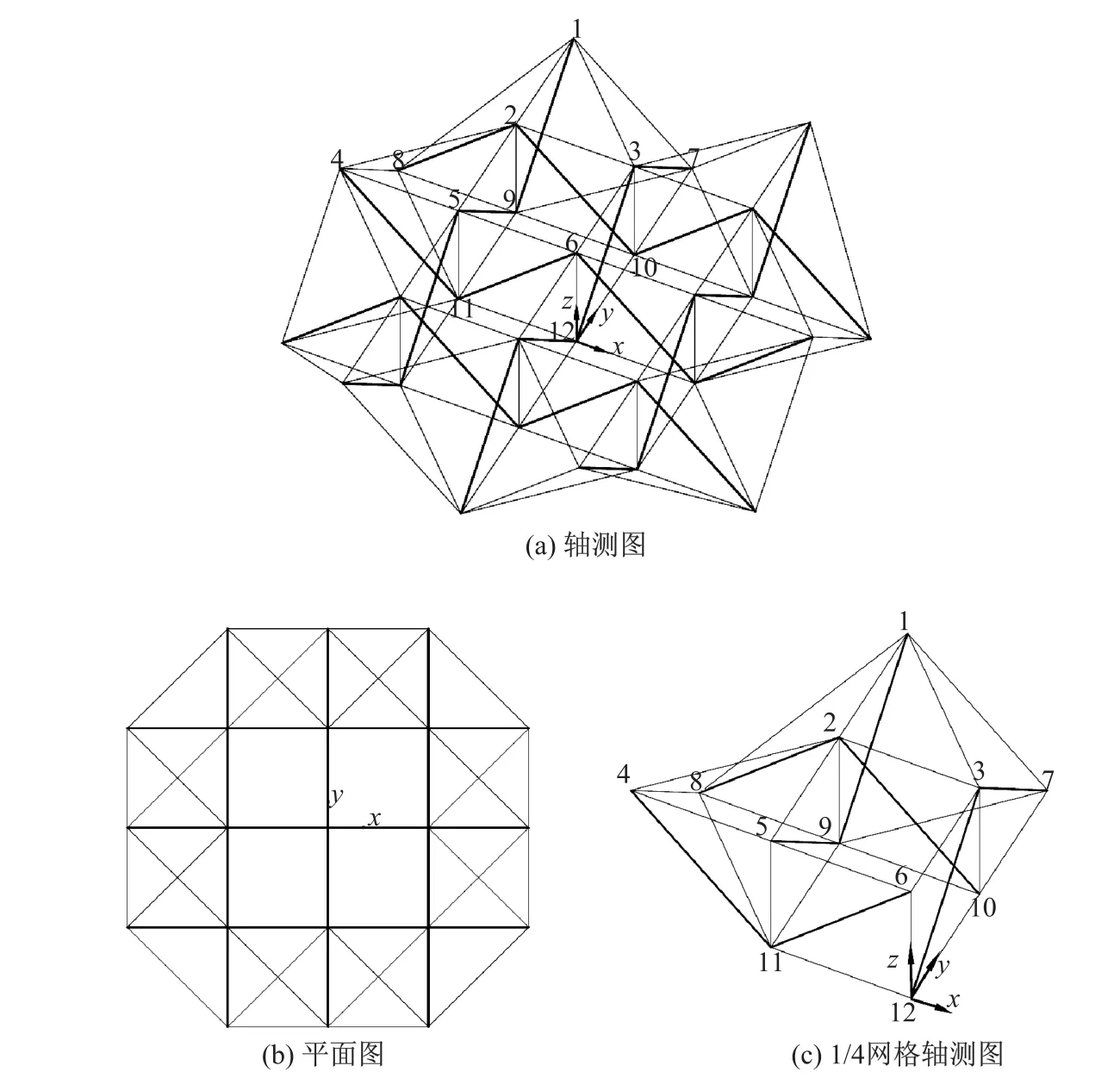
图1 拉索/压杆体系Fig.1 Cable-strut system

与节点编号相对应的拉索、压杆单元的初始给定长度如表1∼4所示,其中所有压杆的初始给定长度均相同(2 262.742 mm),所有与坐标轴方向一致的层间垂直索(2-9,3-10,5-11, 6-12)及上、下层索的长度均相同(1 600.000 mm).

首先需确定体系的初始态,计算中假定所有单元的轴向刚度EA=1.0×106,节点不平衡力最大值满足给定精度ε=1.0×10−6,所有压杆的初始给定内力为−30.000 kN(压为负),所有拉索的初始给定内力为30.000 kN(拉为正).采用动力松弛法求得各单元在初始态的内力及长度如表1∼4所示.由表可见,体系的内力分布比较均匀,其中压杆的内力分布在−32.384∼−34.909 kN之间;上、下层索单元的内力有较大差别,在2.526∼10.068 kN之间;层间垂直索的内力分布在47.021∼48.244 kN之间;层间斜索的内力分布在16.192∼22.924 kN之间.

采用索-钢组合和索-铝合金组合分别确定体系的第一荷载态,区别在于压杆分别采用钢管和铝合金圆管.计算中考虑节点自重,节点采用螺栓球节点BS100[11],拉索采用钢丝绳结构1×37[12],钢管采用焊接钢管[13],铝合金圆管采用弱硬化铝合金挤压无缝圆管(牌号6061;状态T6)[4,14],压杆、拉索的截面尺寸如表1∼4所示.由于体系属于自应力作用下的自平衡体系,参考现行《空间网格结构技术规程》[5],网架可采用上弦或下弦支承方式,计算中假定仅在上层外节点处(对应于1/4网格的节点1,4)有竖向固定支承,即支座节点仅承受体系的竖向自重.无需如索网、索膜等预应力体系所需的强大水平支承,这也是自应力体系与预应力体系相比具有的一大优势.

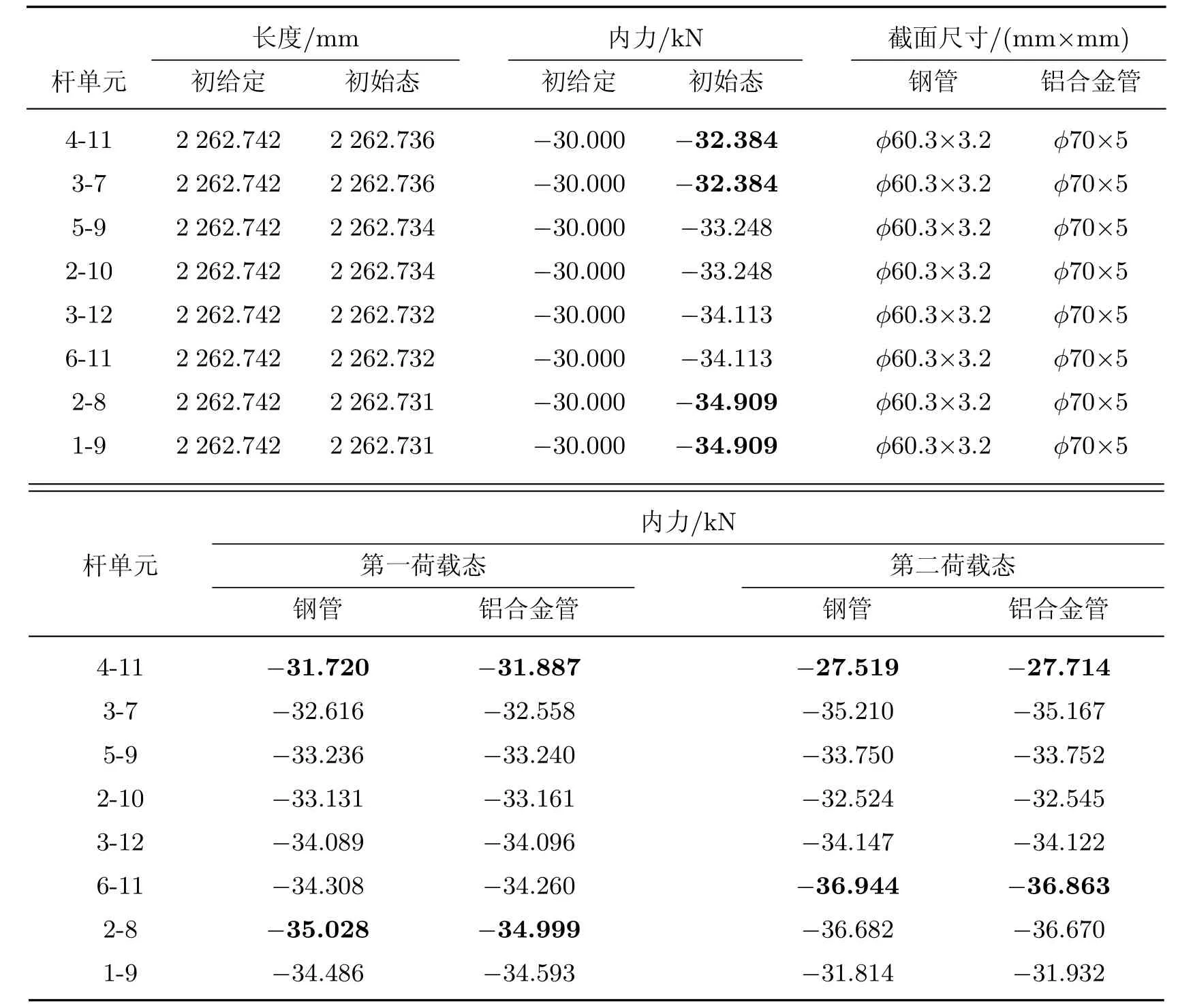
表1 初始态与荷载态杆单元长度及内力Table 1 Element forces and lengths of struts in initial and load states

表2 初始态与荷载态上层索单元长度及内力Table 2 Element forces and lengths of upper layer cables in initial and load states

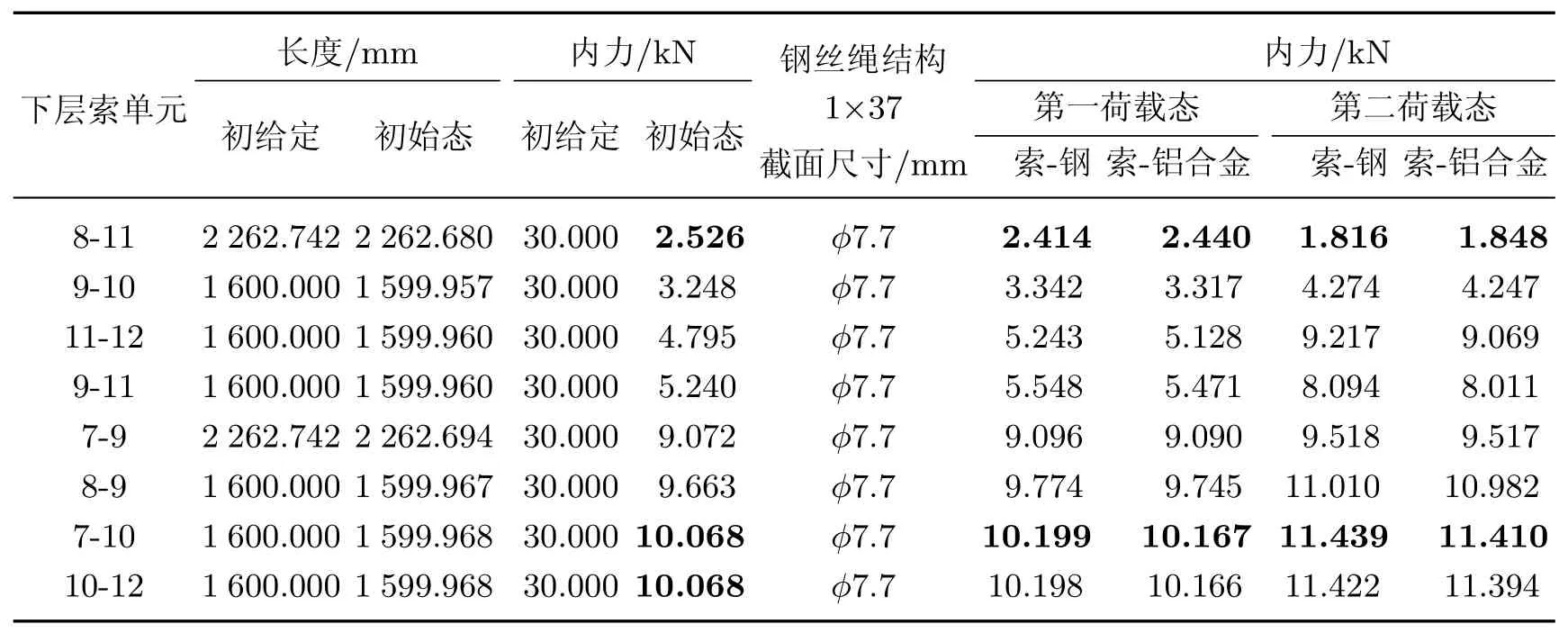
表3 初始态与荷载态下层索单元长度及内力Table 3 Element forces and lengths of lower layer cables in initial and load states

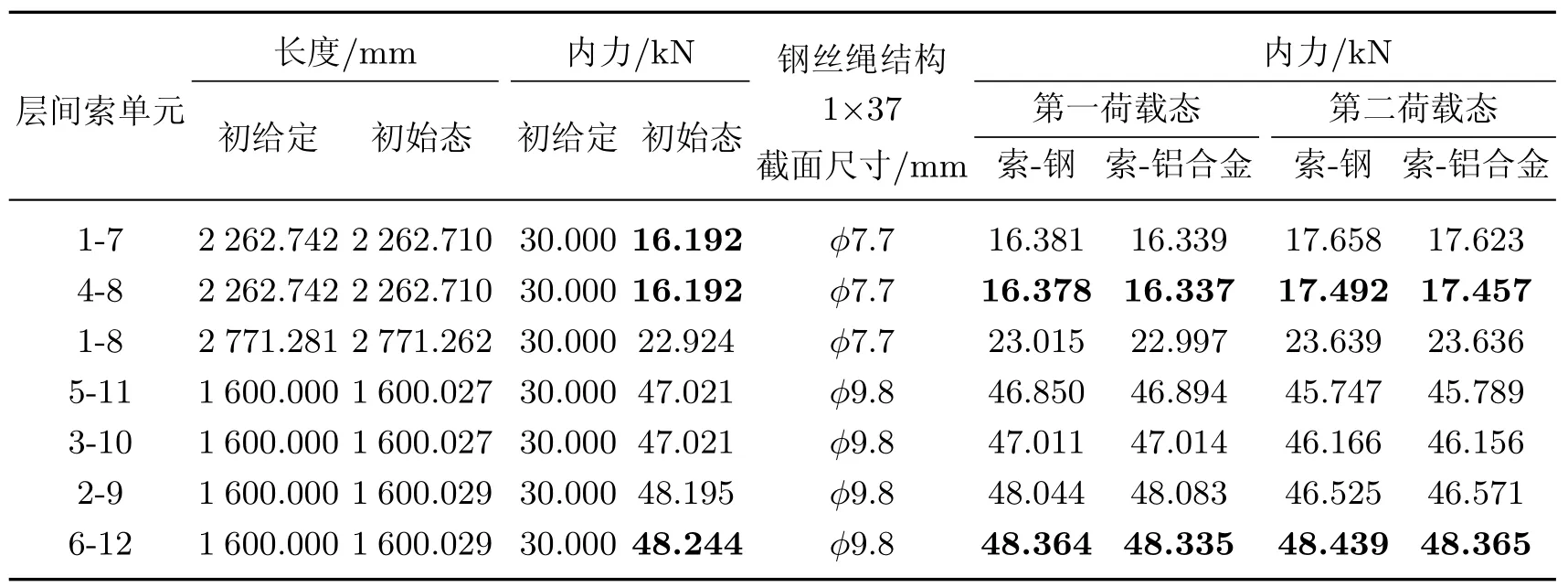
表4 初始态与荷载态层间斜索和垂直索单元长度及内力Table 4 Element forces and lengths of diagonal/vertical cables in initial and load states

对于第一、第二荷载态,计算中的收敛准则同时以位移准则、残余力准则和能量准则来控制,分别取εD=1.0×10−3,εF=1.0×10−6,εE=1.0×10−8.对于钢材取弹性模量E=2.06× 105N/mm2[15],对于拉索(单股钢丝绳)取E=1.4×105N/mm2[6],对于铝合金取E=7.0× 104N/mm2[4].

第一荷载态中各单元的内力如表1∼4所示,从表中可以看出,当压杆分别采用钢管和铝合金圆管时,体系在自重作用下的内力分布差别不大.而且由初始态到第一荷载态体系的最大竖向位移均为中心节点12(索-钢组合:−0.587 mm;索-铝合金组合:−0.449 mm);竖向支座反力也都不大(索-钢组合:节点1为0.588 kN,节点4为0.840 kN;索-铝合金组合:节点1为0.453 kN,节点4为0.644 kN),主要原因在于体系在初始态已具有较大刚度.此外,尽管拉索、压杆在初始态都具有较大的内力,但它们是自平衡的,各支座仅承受体系的自重,这也使得该体系与预应力体系(如索网、索膜、索穹顶等)相比具有较大优势.

在第一荷载态确定的基础上,第二荷载态[6,16]考虑轻型屋面板,自重取0.3 kN/m2,屋面活荷载为0.5 kN/m2.本研究考虑荷载基本组合为1.0×自应力+1.2×恒载+1.4×活载,以及荷载标准组合为1.0×自应力+1.0×恒载+1.0×活载(用于计算体系挠度).计算中假定在上层外节点处(对应于1/4网格的节点1,4)有竖向固定支承,水平向为弹性支承,弹簧刚度为0.5 kN/mm.

第二荷载态体系的最大竖向位移均为中心节点12(索-钢组合:−3.323 mm;索-铝合金组合:−3.381 mm).索-钢组合体系的竖向支座反力:节点1为5.547 kN,节点4为7.197 kN;索-铝合金组合体系的竖向支座反力:节点1为5.418 kN,节点4为6.990 kN.第二荷载态各单元的内力如表1∼4所示,从表中可看出,体系在第二荷载态仍具有较强的抵抗外部荷载的能力,除少数自应力值较小的上、下层索外,无论是拉索还是压杆,其内力的变化幅度相对于自应力都不大,仅有小幅度的增减,这也表明了这种自应力体系的优越性.一旦确定了初始态,体系就具有了较大的初始刚度和较强的抵抗外部荷载的能力.

从索-钢组合和索-铝合金组合的对比中可以看出,铝合金的弹性模量仅为拉索的1/2,接近于钢材的1/3;钢材的质量密度ρ=7 850 kg/m3,铝合金的质量密度ρ=2 700 kg/m3,也接近于钢材的1/3.本算例中,整个模型水平投影面积为35.84 m2,钢制螺栓球节点的自重为197.3 kg,钢丝绳索的自重为43.5 kg,钢管的自重为244.7 kg,铝合金圆管的自重为149.7 kg,不足钢管自重的62%.索-钢组合体系总重485.5 kg,耗钢量不足14 kg/m2;索-铝合金组合体系总重390.5 kg,耗钢量不足11.0 kg/m2.如果体系的节点采用铝合金螺栓球节点[17],则体系的自重将有进一步较大幅度的减轻.

无论是在第一荷载态还是第二荷载态,索-钢组合体系和索-铝合金组合体系的最大挠度及单元内力分布都差别不大,这表明铝合金材料比钢材更具有轻质高强的优势.特别是随着跨度的增大,当体系自重的影响越来越大时,采用铝合金材料的优势将更加明显.

上述算例表明,采用动力松驰法确定体系初始态,以及采用牛顿-拉弗森法确定体系荷载态具有实用性和优越性,为索-钢/铝合金组合结构在实际工程中的推广应用奠定了基础.

4 结论

(1)索-钢/铝合金组合结构是由拉索和压杆(钢管/铝合金圆管)组成的自应力状态下的稳定自平衡体系.体系的自应力初始态可采用动力松弛法来确定,在仅考虑体系自重的第一荷载态和有外部荷载作用的第二荷载态的情况下,需考虑几何非线性的影响,可采用牛顿-拉弗森法通过迭代求解非线性方程组来确定荷载态结构几何与内力分布.

(2)索-钢组合结构和索-铝合金组合结构的受力机理相似,在初始态由于自应力的存在,体系均具有较大的刚度;在第一荷载态,支座节点仅承受体系的自重作用;在第二荷载态,各单元的内力与自应力相比变化幅度不大,表明体系具有较好的抵抗外部荷载的能力.

(3)索-钢/铝合金组合结构具有自重轻、受力性能好和支座负担轻的优点;与索-钢组合结构相比,索-铝合金组合结构可进一步减轻体系自重,这在大跨度结构中更具优势.

[1]莫特罗.张拉整体——未来的结构体系[M].薛素铎,刘迎春,译.北京:中国建筑工业出版社,2007: 7-30,197-226.

[2]Stamenovic D.Effects of cytoskeletal prestress on cell rheological behaviour[J].Acta Biomaterialia,2005,1(3):255-262.

[3]刘锡良,陈志华.一种新型空间结构——张拉整体体系[J].土木工程学报,1995,28(4):52-57.

[4]中华人民共和国建设部.GB 50429—2007铝合金结构设计规范[S].北京:中国计划出版社,2008.

[5]中华人民共和国住房和城乡建设部.JGJ 7—2010空间网格结构技术规程[S].北京:中国建筑工业出版社,2010.

[6]中华人民共和国住房和城乡建设部.JGJ 257—2012索结构技术规程[S].北京:中国建筑工业出版社,2012.

[7]Barnes M R.Form-finding and analysis of prestressed nets and membranes[J].Computers and Structures,1988,30:685-695.

[8]张莉.张拉结构形状确定理论研究[D].上海:同济大学,2000.

[9]Zhang L,Maurin B,Motro R.Form-finding of nonregular tensegrity systems[J].ASCE Journal of Structural Engineering,2006,132(9):1435-1440.

[10]Bathe K J.Finite element procedures[M].New Jersey:Prentice-Hall,1996:754-765.

[11]中华人民共和国住房和城乡建设部.JG/T 10—2009钢网架螺栓球节点[S].北京:中国标准出版社,2009.

[12]中国钢铁工业协会.GB/T 20118—2006一般用途钢丝绳[S].北京:中国标准出版社,2006.

[13]中国钢铁工业协会.GB/T 21835—2008焊接钢管尺寸及单位长度重量[S].北京:中国标准出版社, 2008.

[14]全国有色金属标准化技术委员会.GB/T 4436—2012铝及铝合金管材外形尺寸及允许偏差[S].北京:中国标准出版社,2013.

[15]中华人民共和国建设部.GB 50017—2003钢结构设计规范[S].北京:中国计划出版社,2003.

[16]中华人民共和国住房和城乡建设部.GB 50009—2012建筑结构荷载规范[S].北京:中国建筑工业出版社,2012.

[17]上海市工程建设标准化办公室.DGJ08—95—2001铝合金格构结构技术规程(试行)[S].上海:上海市工程建设标准化办公室,2001.

Initial state determination and static analysis of composite cable and steel/aluminum structures

ZHANG Li
(Department of Civil Engineering,Shanghai University,Shanghai 200072,China)

Composite cable and steel/aluminum structure is a new system.It is in a selfstress and stable self-equilibrated state,comprising a continuous set of tension members (cables)and a discontinuous set of compression components(steel pipes or alloy tubes). Starting from an initial specified geometry and topology,the initial self-stress is determined using a dynamic relaxation method.The behavior of the structure is analyzed for safely resisting the self-weight and applied static load using the Newton-Raphson method.To understand its mechanical property,steel pipes and alloy tubes are used as compression members respectively in the two kinds of composite structures.Application of the process is shown with a numerical example.It is concluded that that improvement in engineering application of the composite cable and steel/aluminum structure has been achieved.

composite cable and steel/aluminum structure;initial self-stress state;mechanical property

TU 398.9

A

1007-2861(2015)05-0631-09

10.3969/j.issn.1007-2861.2014.05.009

2014-10-10

上海大学创新基金资助项目(10011811001)

张莉(1969—),女,副教授,博士,研究方向为空间结构.E-mail：l.zhang@shu.edu.cn