一类带马尔科夫参数的不确定性系统鲁棒控制器设计

王瑾，董泽

（华北电力大学 控制科学与计算机学院，河北 保定 071002）

现实系统中往往存在许多不确定因素，将这些不确定因素建模为随机过程可以使系统更真实、更准确地反映实际工程技术中的系统运动规律，但是参数的不确定性又会影响系统控制性能的稳定性以及其他性能［1］，因此，要在系统中引入鲁棒控制确保不确定系统的稳定性.而马尔科夫跳变系统是一类系统模态受马尔科夫链约束的混杂线性系统，其连续特性和离散特性并存［2］.实际工业过程中，由于外界工作环境变化、参数发生变化、元件失效及连接中断等突发因素会造成系统结构的变化，马尔可夫跳跃系统能够描述此类具有结构突变的实际工业过程而获得了广泛的关注研究.此外，在工程实践中，采用现代控制理论方法所设计的控制系统一般难以达到期望的性能，稳定性也难以保证，而鲁棒控制理论基于外部扰动不确定性与系统模型参数不确定性的考虑下，对系统鲁棒稳定性问题进行研究，弥补了现代控制理论需精确数学模型的缺点，使系统的分析方法更加有效和实用［3］.本文研究的带有马尔科夫参数的不确定系统，可以较好地体现实际系统的特性，对于随即参数的控制有较好的探究意义.本文通过得到系统的稳定性条件来设计鲁棒控制器，完成对结构具有复杂性和突变性的系统的更好控制.

1 不确定性系统

1.1 带有马尔科夫跳变参数的不确定性系统模型

对于实际控制对象，尤其是随机性较强的对象，较难得到准确模型或模型形式复杂，以Markovian跳变系统来描述控制对象会有较好的效果.状态空间的不确定性模型［4］.

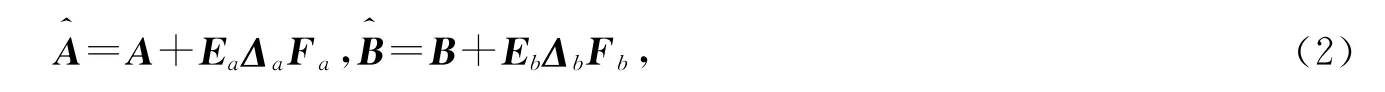
其中，A，B 是适当维数的实常数矩阵，描述了系统的名义模型，即忽略了模型的不确定性后得到的系统模型；Δa和Δb是不确定参数矩阵，反映了系统模型中的参数不确定性，且其中的一些不确定参数可能是重复的；Ea，Eb，Fa，Fb是适当维数的常数矩阵，它们反映了不确定参数是如何影响系统模型的，即反映了模型不确定性的结构.模型的不确定参数尽管是未知的，但总可以设定它们在某个有界的范围内变化，这个变化范围的大小直接影响到系统性能.

系统模型（2）中的不确定因素可写成

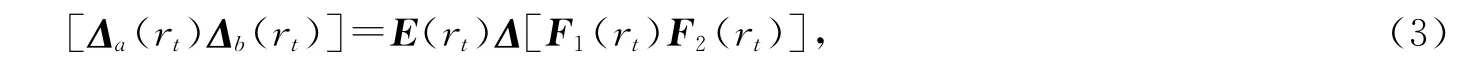
其中ΔTΔ≤I，rt为马尔科夫跳变参数.

1.2 模型的自由系统

对于系统（1），当u（t）＝0时，系统为自由系统，在自由系统中，不确定部分为0时，系统为名义系统［5］，鲁棒稳定性研究即是研究自由系统的稳定性，考虑自由系统

其中，x∈Rn是系统的状态向量为实常数向量的函数.所要研究的问题是：给出系统（4）的鲁棒稳定条件，在该条件下，对于所有不确定参数，系统都是渐进稳定的.

2 系统的鲁棒控制器设计

2.1 鲁棒稳定性条件

已知系统模型，要想进行控制器的设计，首先要得到其稳定性的条件.根据模型表达式，选择Lyapunov稳定判据进行求取，因此有以下定理：

定理1 系统（4）对于任意参数ε＞0，存在线性矩阵不等式

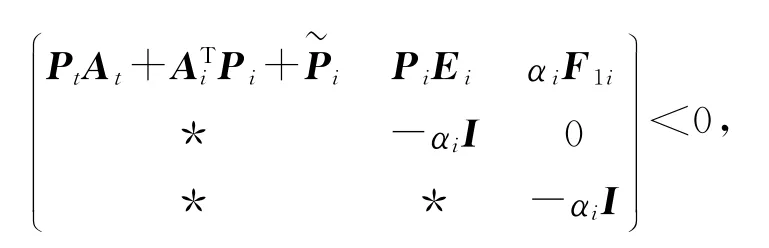
则可知系统鲁棒稳定［6］.

证明：已知系统（4）为自由系统模型，设Lyapunov能量方程为V（x）＝xT（t）Pix（t），对能量方程进行弱微分，可得

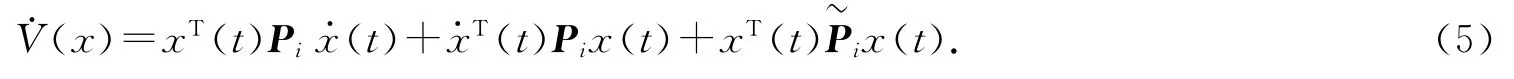
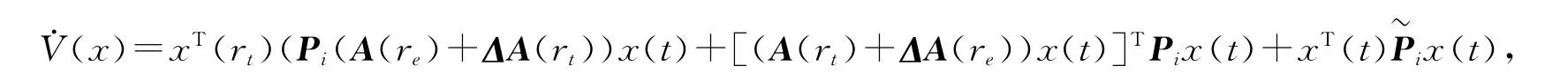
将不确定因素和确定因素分开，得到

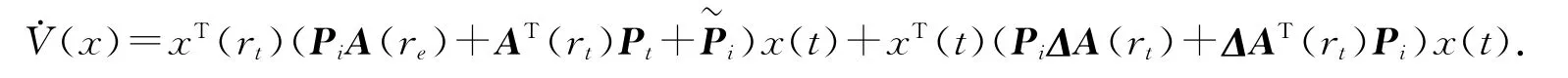
在下文中，以Ai，Ei，Fi代替A（rt），E（rt），F（rt）.由式（3）可知上式中的不确定因素可以写成

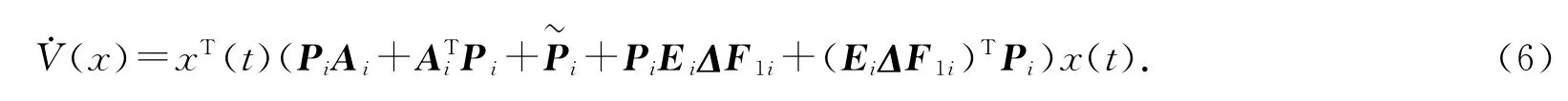
定理2［7］对于给定对称矩阵Q，适当维度矩阵D，E 和F（t），若存在Q＋DF（t）E＋（DF（t）E）T＜0，对所有满足FT（t）F（t）≤I的矩阵F（t）成立，则当且仅当存在一个标量ε＞0，有Q＋εDDT＋ε－1ETE＜0.

即

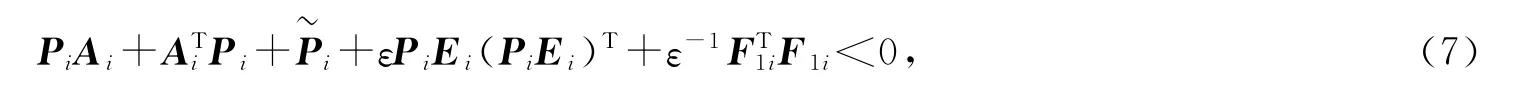
定理3［7］对于如下的线性矩阵不等式，

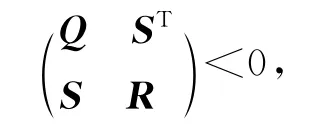
其中Q＝QT，R＝RT，S 为适当维度的矩阵，其等价于R＞0，Q＋STR－1S＞0.

由定理3可知，式（7）可写成

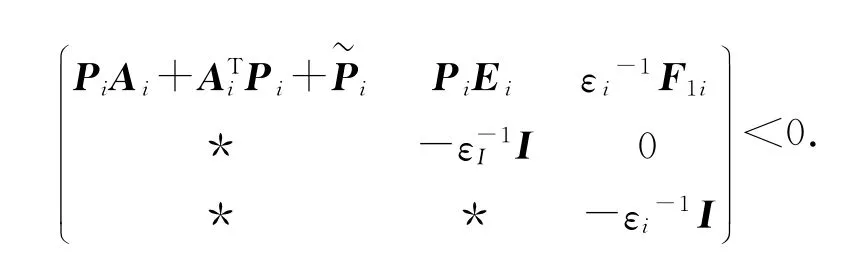
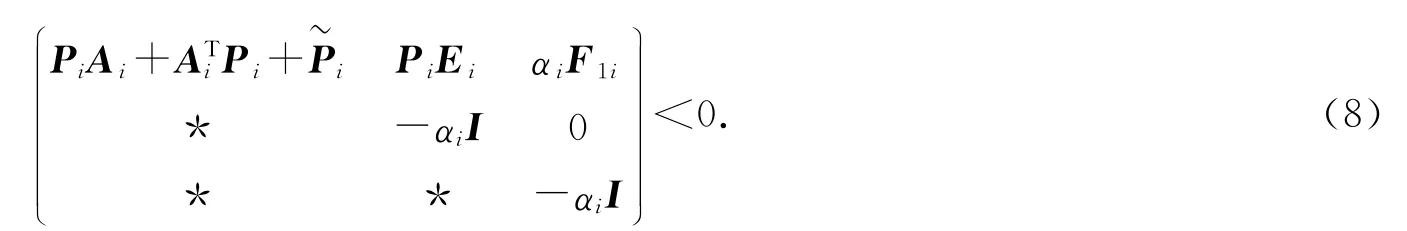
由式（8）可知，可以证明该不等式为系统的鲁棒稳定性条件。

2.2 鲁棒控制器的设计

已知系统的鲁棒稳定性条件，要进行控制器设计，在自由系统基础上要考虑系统的输入部分，因此有以下定理：

定理4 对于给定的Ai＞0，如果存在矩阵Xi，Yi满足，那么控制器是存在的［8］，且控制器形如

证明：已知连续跳变Markovian系统模型为

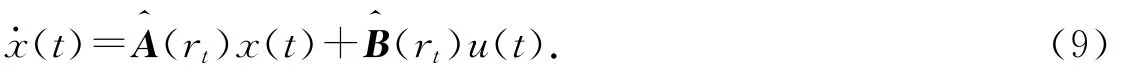
由稳定性条件和系统模型可知，控制器模型为u（t）＝Kix（t）.

由Lyapunov稳定性条件，设能量方程为V＝xTPix，对能量方程进行弱微分，可得

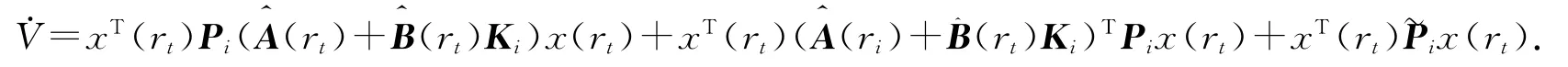
将上式中的确定因素和不确定因素分开得到

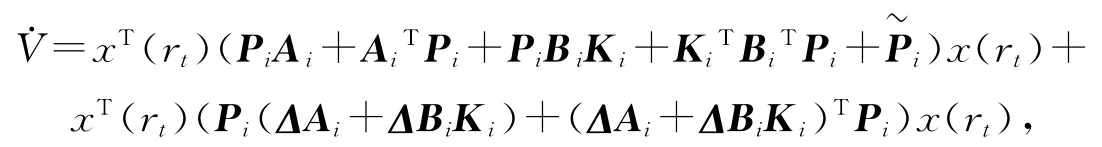
其中，为了书写方便，使用Ai，Bi，ΔAi，ΔBi代替A（rt），B（rt），ΔA（rt），ΔB（rt）.结合式（2），上式中的不确定因素可写为，根据定理2，可知D＝PiEi，E＝［F1iF2iKi］.

要求证Q＋DF（t）E＋（DF（t）E）T＜0，即求证存在参数εi＞0使得，即

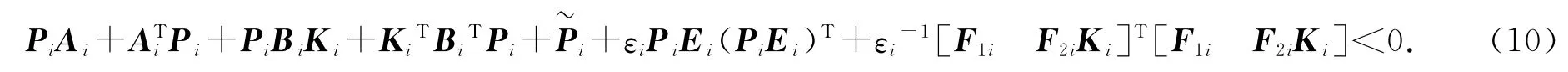
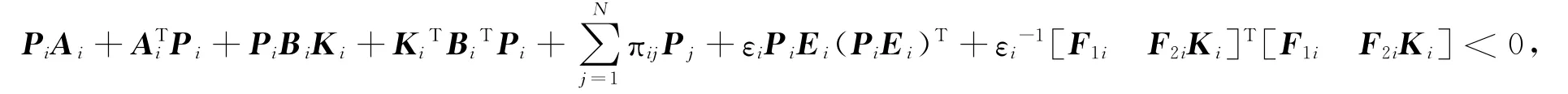
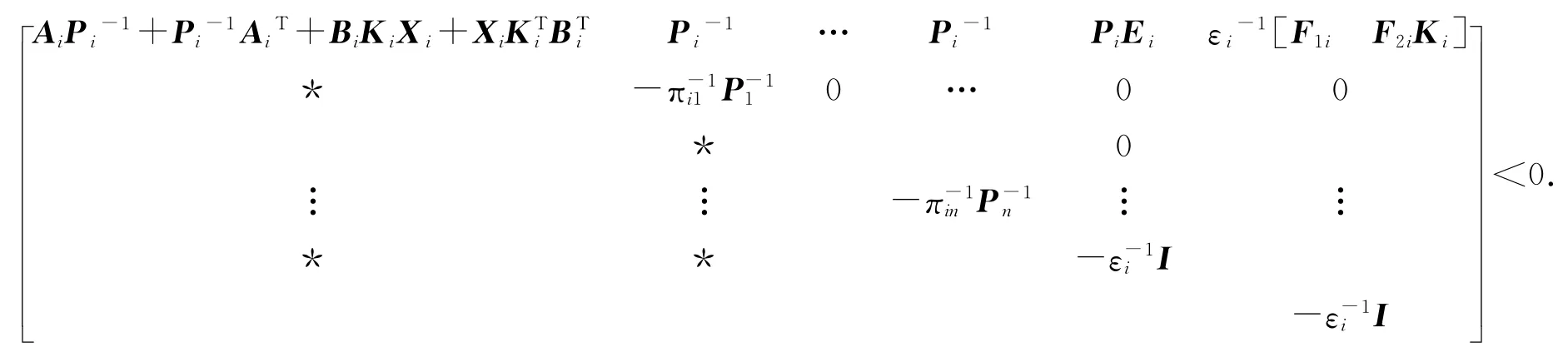
令Yi＝KiXi，得

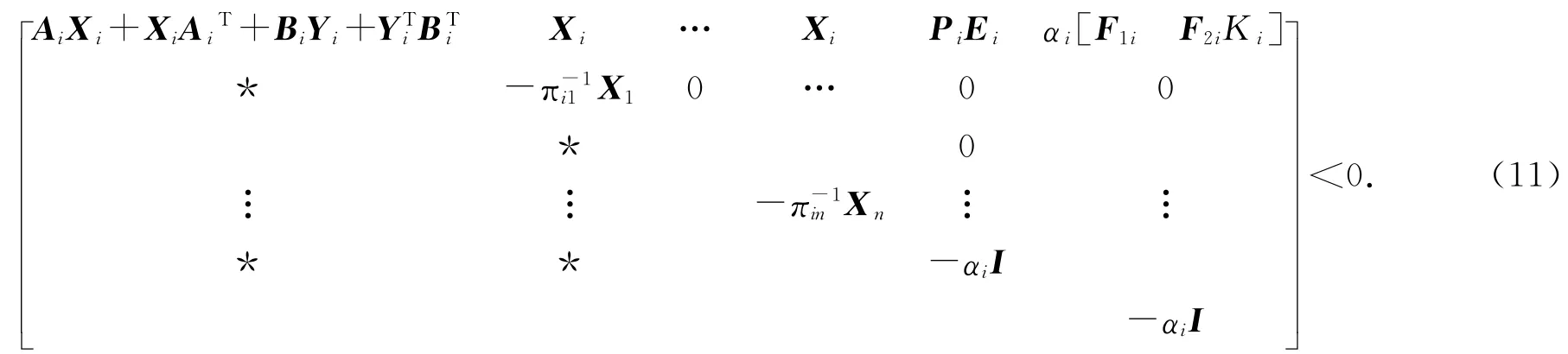
由上式可知，式（11）即为系统鲁棒稳定性条件，可根据式（11）进行控制器形式的求取.其中，在实际仿真中，一般忽略系统输入的不确定影响即使ΔB＝0，即输入变量中的不确定因素为0，所以上式F2i＝0，得到如下矩阵不等式：

式（12）即为忽略输入量不确定性的鲁棒稳定性条件，在进行仿真实验时即选取式（12）进行仿真.

3 数值算例

由式（12）可知控制器的LMIs形式，已知系统1与系统2以及不确定因素如下：

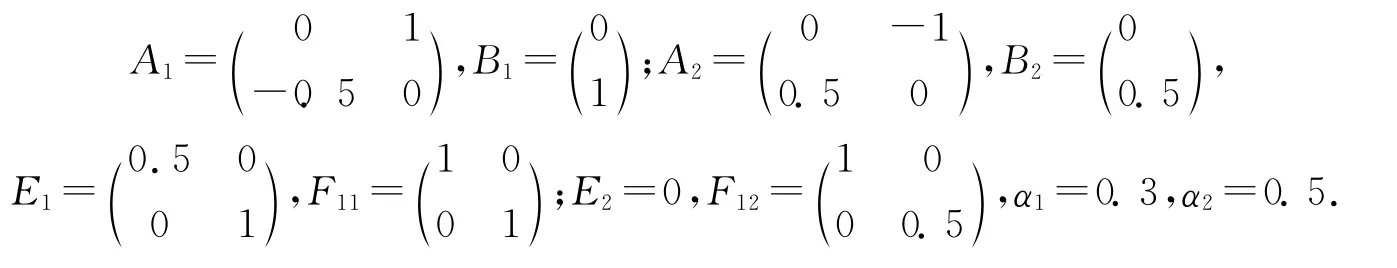
通过LMIs仿真得到

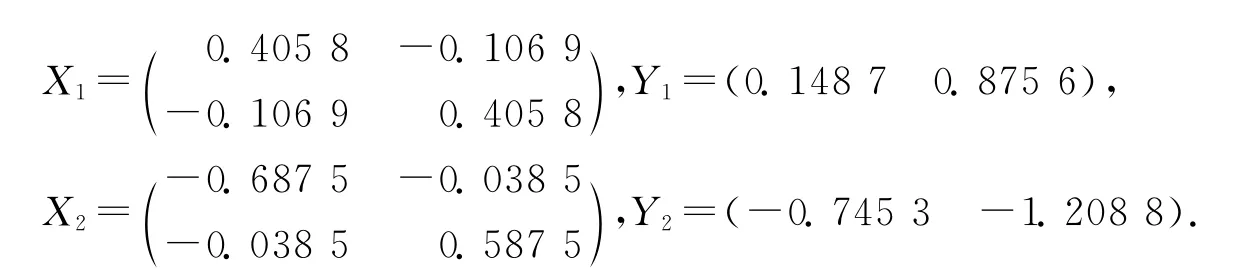
可得到控制器结果为K1＝［1.238 7 1.448 0］；K2＝［0.759 8 2.145 5］；t＝－0.423 56.

由结果可知，使用该方法可得到简单不确定系统的鲁棒控制器参数，且t值在单位圆的负平面，说明其能量呈现衰减的趋势，系统最终控制在稳定的状态，因此，可知该控制器可对不确定系统进行控制.

4 结束语

针对带有Markovian参数的不确定性系统，通过Lyapunov稳定性原理以及线性矩阵不等式中的Schur补原理以及范数有界矩阵消除法对系统的稳定性条件进行推导及证明，进行了稳定性分析和鲁棒稳定控制器的设计，得到了系统的鲁棒稳定性条件和控制器形式，并通过对LMIs方法的综合运用，进行了一系列仿真，得到了数值算例的稳定性条件和控制器参数，实现了对系统的不确定参数造成的随机性进行控制，保证了不确定性系统的稳定性.

［1］ 关永强.参数不确定性系统的鲁棒稳定性研究［D］.湘潭：湘潭大学，2010.

［2］ 王曰英，周平方，陈丽，等.马尔可夫跳跃系统的鲁棒故障检测［J］.电力自动化设备，2010，30（5）：83－84.WANG Yueying，ZHOU Pingfang，CHEN Li，et al.Robust fault detection of Markovian system［J］.Electric Power Automation Equipment，2010，30（5）：83－84.

［3］ MAHMOUD M S，SHI Ping.Robust stability，stabilization and H－∞control of time－delay systems with Markovian jump parameters［J］.Robust Nonlinear Control，2003，13（3）：755－784

［4］ 俞力.鲁棒控制－线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.

［5］ 丁强，钟麦英.一类线性Markov跳跃区间时滞系统的鲁棒H－∞故障检测滤波器设计［J］.控制与决策，2011，26（5）：712－715. DING Qiang，ZHONG Maiying.Design of robust H－∞fault detection filter for a class of linear Markovian jump systems with interval time－delay［J］.Control and decision，2011，26（5）：712－715.

［6］ 姚秀明.混杂Markovian 跳跃系统的分析与综合［D］.哈尔滨：哈尔滨工业大学，2010.

［7］ XIE Lihua.Output feedback H－∞control of systems with parameter uncertainty［J］.Int J Control，1996，63（4）：741－751.

［8］ 叶思隽，王新民，张清江，等.不确定系统混合H2／H∞鲁棒控制的直接迭代LMI方法［J］.控制理论与应用，2011，28（2）：248－251.YE Sijun，WANG Xinmin，ZHANG Qingjiang，et al.Direct iterative LMI－based approach of mixed H－two／H－infinity robust control for uncertain systems［J］.Control Theory and Application，2011，28（2）：248－251.