加筋壁板压电分流阻尼抑振系统优化的研究

张建君++马天兵

摘要：针对加筋壁板压电分流阻尼系统抑振效果不理想的问题，提出对抑振系统进行优化，具体是通过理论分析对压电分流回路参数进行优化，和在考虑压电元件粘贴的情况下，采用ANSYS对四边固支的加筋壁板进行压电片粘贴位置布局优化。最后将优化应用于一四边固支的加筋壁板振动控制上，实验结果表明抑振控制效果明显，验证了加筋壁板压电分流阻尼抑振系统优化的有效性。

关键词：压电分流；布局；参数；优化；加筋壁板；

中图分类号：TN912文献标志码：A

文章编号：1672-1098（2015）01-0070-05

压电分流阻尼抑振系统[1]，是一种被动振动控制方法， 该方法易于实现， 不需要搭建复杂的电路， 且额外添加要素较少， 附加的质量较少， 在被动抑振领域广泛应用。其技术的原理是通过压电分流电路将结构振动产生的机械能通过压电片的变形转化为电能， 以发热的方式消耗掉或者以电能的形式被收集， 从而产生抑制振动的阻尼。 由于抑振过程中机械能被以放热方式消耗掉，这种转化过程不可逆， 使这种振动控制方法拥有了较好的鲁棒性。

在此系统中，压电分流电路中电阻、电容等元件的取值和压电元件配置是影响抑制振动效果的关键问题之一。一方面因为压电分流回路的参数选择决定利用正压电效应产生的机械能能否最大化的转化成电能输出；另一方面，压电元件的粘贴位置决定了压电元件受到结构振动诱发的应变量大小，也决定了压电元件产生的电荷量，即分流电路的电流强度[2]；因此，可以对系统进行优化以得到好的控制效果。文献[3]提出四种分流电路的谐振技术[3]。程有伟提出对板梁结构作动器个数和位置优化[4]。

本文通过理论分析和优化计算，提出对加筋壁板压电分流阻尼抑振系统中压电分流回路参数和压电元件的布局优化，最后将优化应用于一四边固支的加筋壁板振动控制上，实验结果表明振动控制效果明显，验证了加筋壁板压电分流阻尼抑振系统优化的有效性。

1压电分流回路的参数优化

压电分流阻尼系统用于加筋壁板被动振动控制，是利用压电元件的压电效应[5]，将机械振动的机械能转变成压电元件应变产生的电场能，通过一个与之并联的电阻——电感电路，形成RLC 分流谐振回路。压电材料因其自身特性充当着电容和电源，电场能通过谐振电路以散热消耗掉，从而人为的为机械振动系统添加了抑制振动的阻尼。

设压电加筋壁板作单模态振动，则系统在做传递函数变换上可看作弹簧阻尼系统，压电谐振回路充当抑振系统阻尼。则压电加筋壁板系统在激振力作用下的振动微分方程的拉氏变换为[6]

[Ms2+Z（s）s+K]X（s）=F（s） （1）

式中：Z（s）为压电分流系统的阻尼，K为系统刚度，F（s）为激振力，X（s）为响应位移，所以系统的位移传递函数为

X（s）F（s）=1Ms2+Z（s）+K （2）

对上式化简并采用去量纲法

xxST=（δ2+μ2rδ+μ2）（δ2+1）（δ2+μ2rδ+μ2）+K231 （δ2+μ2rδ） （3）

式（3）描述的是结构在外部激励下的位移响应，式中各物理量的表达式为

XST=FK+KE11 ；

δ=sωshortn ； μ=ωeωopenn ；

r=RCs3 ωshortn； ωshortn=K+KE11M；

ωe=1LCs3 ； K231=KE11K+KE11 ·K2311-K231

式中：KE11 和ωe分别是压电陶瓷在常电场下的刚度和RLC串联谐振回路的谐振频率；ωopenn 和ωshortn 分别是加筋壁板结构在压电片两极开路和短路情况下的频率；K31是系统结构本身的机电耦合系数；Cs3 是加筋壁板系统结构本身常应力作用下的电容；L为压电片无外界作用下系统本身的电感；R为RLC 分流谐振回路电阻。

拉氏变量s是一个复数，称之为复频率，其虚部代表者系统振动的频率，设其实部为零，则：s=iω，为使下文方便分析，令：g=ωωshortn ，则：δ=g·i。于是方程（3）为

xxST=-g2+μ2rg·i+μ2（1-g2）（μ2rg·i+μ2-g2）+K231 （μ2rg·i-g2）（4）

因为上面推导的传递函数描述的是耦合系统在外界激励下的位移响应，而且系统传递函数是以振动频率ω为自变量的函数，因此需要优化的参数只有μ和r，所以，谐振回路参数优化的实质就是选择合适的μ和r，使系统传递函数幅值最小。压电加筋壁板系统的传递函数的幅值为[7]

|xxST|=（μ2-g2）2+（μ2rg）2[（1-g2）（μ2-g2）-k231 g2]2+[（1-g2）μ2rg+k231 μ2rg]2（5）

μ和r的值分别是由电感和电阻的值决定的， 所以， 选择合适的μ和r的值就是选择合适的谐振电路元件电感和电阻的值。 分别取r=0，r=∞，r=011和r=003（在 0～∞之间任意取值），代入方程，再任意选取方程中的μ和k231，令μ=1012，k231=00012，代入到方程（5）中，得到传递函数的幅值对于频率g的变换曲线，如图1所示。

1. r=∞；2. r=0.11；3. r=0；4. r=0.03

无量纲频率g

图1系统传递函数幅值曲线

从图1可以看出， 不论r取何值， 幅值曲线都要经过A， B两点。 即此时控制系统传递函数幅值响应与阻尼大小无关。 那么选择特殊点r=0和r=∞，其两点所对应的g值幅值相等，即得方程

|u2-g2（1-g2）（u2-g2）+k31g2|=|11-g2+k231| （6）

将方程（6）去掉绝对值，取负值得endprint

g4-（1+k231+u2）g2+（1+05k231）u2=0 （7）

由韦达定理得μ的最优值μopt=1+k231 ，将此最优值带入式（7）得r的最优值：ropt=2k31/（1+k231）。由μ和r的值与L和R的值之间的关系，可知二者最优值为

Lopt=1（ωopenn）2（1+k231）Cs3 ；

Ropt=2k31ωshortn Cs3 （1+k231） （8）

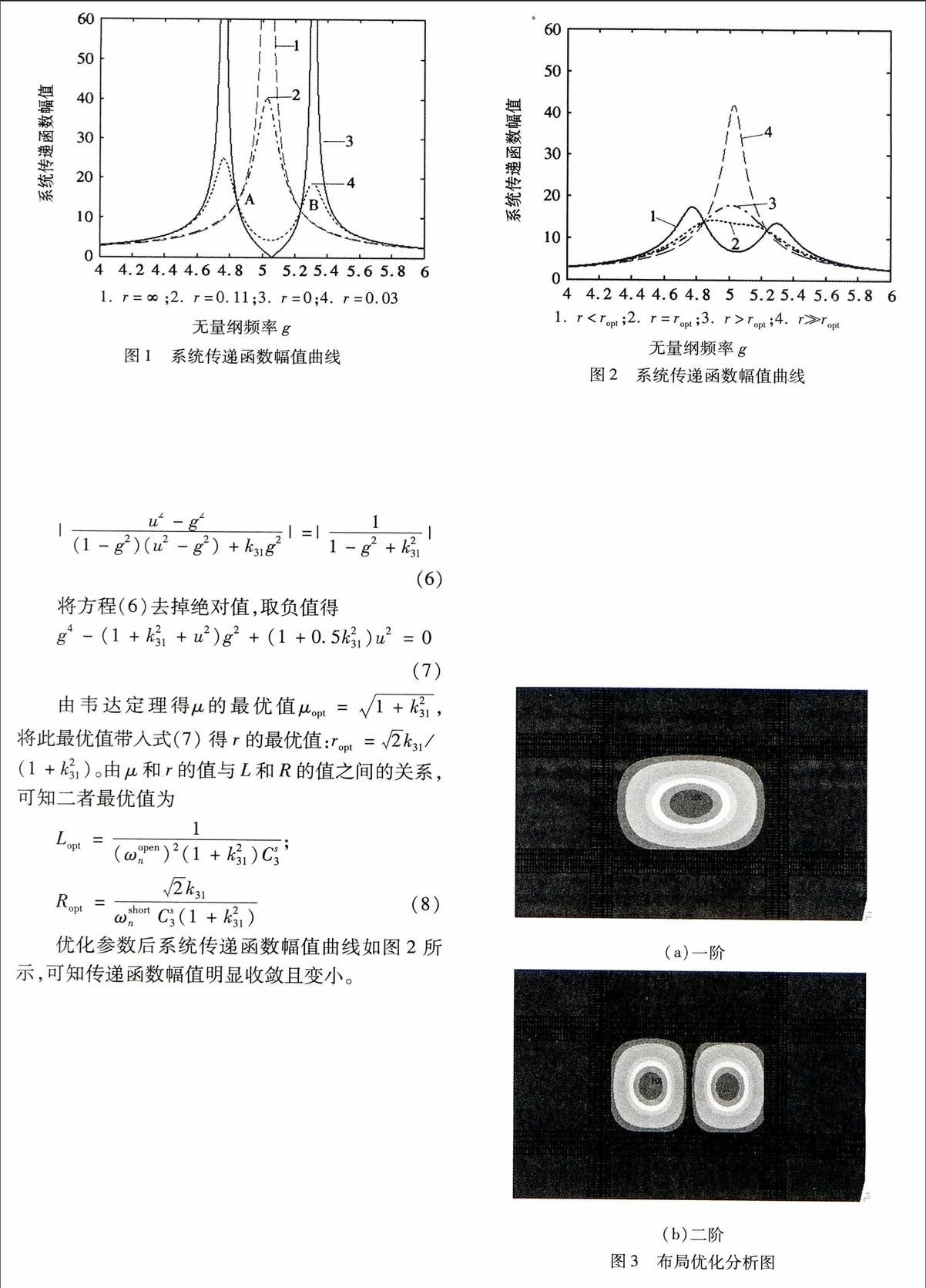
优化参数后系统传递函数幅值曲线如图2所示，可知传递函数幅值明显收敛且变小。

1. rropt；4. rropt

无量纲频率g

图2系统传递函数幅值曲线

2压电片的粘贴布局优化

压电元件布局优化的目的是为了使压电元件极化表面总电荷量Q变大[8]，Q的值越大，分流电路所消耗的能量越多，抑振效果就越好；优化设计变量为压电元件的形心坐标（x，y），使其形心坐标在加筋壁板模态振动应变最大处，一般是设定其取值范围进行优化计算。

对于加筋壁板的某一阶模态响应，改变压电元件在壁板上的位置，那么其各个单元的x向和y向应变的代数和就会发生变化，即压电元件极化表面的Q也发生了变化。

因此，利用ANSYS分析加筋壁板的前两阶振动模态，然后优化各压电元件的位置使Q达到最大值。本文采用ANSYS建立有限元模型并进行模态分析，首先建立实验装置匹配的有限元模型，加筋壁板尺寸为400 mm×600 mm×12 mm，加强筋为Z型截面梁，材料为铝合金，对模型节点施加ALL-DOF全约束，分析结果如图3所示。

（a）一阶

（b）二阶

图3布局优化分析图

由图3分析结果可知前两阶振动模态频率分别为：18914 Hz和29921 Hz。图3中椭圆中心所在的地方为应变最大处，也就是布局优化的坐标点。

3实验

由于外界的激励振动对加筋壁板的结构损坏主要集中在前几阶模态的振动上，因此本文主要针对加筋壁板的前两阶模态进行控制。实验中选用的分流电路为抑制稳态响应效果最优的传递函数参数优化的RL串联电路，其与压电片共同构成RLC压电分流谐振回路[9]。

实验采用北京波普公司生产的Ws-Z系列振动控制平台，利用Vib′SQR信号软件，采用扫频激励法[10]得到压电片两极开路和短路情况下结构的第1阶固有频率为

f1open=19121 Hz；f1short=18965 Hz

第2阶固有频率为

f2open=30035 Hz；f2short=29973 Hz；

压电片的电容为Cs3=237 nF，则1阶和2阶机电耦合系数：

k231=（f2open-f2short）/f2short=00165

k231=（f 2open-f 2short）/f2short=00041

由式（8）得分流电路中电感和电阻的理论计算的优化值为

1阶：Lopt=1/[（ωopenn）2（1+k231）Cs3]=292 H

Ropt=2k31/ωshortn Cs3 （1+k231）=63365 Ω

2阶：Lopt=1/[（ωopenn）2（1+k231）Cs3]=1181 H

Ropt=2k31/ωshortn Cs3 （1+k231）=20203 Ω

根据上述理论计算结果搭建压电分流电路，并将起到控制振动作用的压电片粘贴于优化的布局位置。

在试验中，信号发生器分别发出1阶19121 Hz和2阶30035 Hz的正弦信号，通过激振器激励加筋壁板，使加筋壁板做受迫振动，粘贴于优化位置的压电片采集信号并通过信号采集仪输入到电脑中。由实验可知，分流电路接通后第1阶和第2阶模态响应的幅值x随时间分别降低到分流电路接通前的441%与375%，取得了不错的抑振效果如图4和图5所示。

t/s

图4第一阶振动模态控制

t/s

图5第二阶振动模态控制

4结论

被动控制抑制振动效果是由压电材料的机-电转换和电路的电-热转换效率决定。本文通过对加筋壁板压电分流阻尼抑振系统的压电分流回路的参数进行优化和压电片粘贴位置的布局优化，并应用于一四边固支的加筋壁板振动控制实验上，实验取得较好的抑振效果，证明了优化的有效性。通过理论和实验分析得到三个结论。

1） 根据要控制的加筋壁板几何模型以及相应的动力学性质，选择一定规格的压电元件，如形状大小、电容大小、层数等。

2） 要确定压电片的粘贴位置，首先要确定加筋壁板在外界激励作用下，壁板表面发生共振所造成位移响应引起应变最大点的坐标。因此，优化前对结构进行模态分析，确定应变最大位置。

3） 在实验中，虽然可以通过对压电分流阻尼系统传递函数进行参数优化的方法计算出使传递函数幅值最小时对应的电阻电感数值，但是由于控制通道的不确定性，以及外界干扰和电路的影响，大多数时候理论计算值并不能与实际情况匹配，因此，计算出来的电感和电阻值与实际优化值有偏差，所以在实际调节时，利用当μ取最优值，且r=0时，无量纲振动频率g等于结构共振频率点，振动输出位移最小这一特性，取RLC电路中电阻R=0，通过调节模拟电感电路中可调电阻电阻值，来寻找实际控制的那一阶的短路共振频率。

参考文献：

[1]HAGOOD N W， VONF FLOTOW A. Damping of s-tructural vibrations with piezoelectric materi-als and passive electrical networks[J].Journal of Sound and Vibration，1991（146）： 243-268.

[2]李凯翔，杨智春.压电分流阻尼系统中压电元 件形状与布局优化[J].压电与声光， 2008，3（2）：183-186.

[3]GEORGE A LESIEUTRE.Vibration Damping and Control Using Shunted Piezoeleetrie Materials [J].The Shoek and Vibration Digest，1998，30（3）： 187-195.

[4]程有伟.智能板梁结构作动器传感器个数与位 置拓扑优化[D].西安：西安电子科技大学，2009.

[5]孙康，张学福.压电学（上、下册）[M].北京：北京国防工业出版社，1986：8-200.

[6]翟太珍.飞机加筋壁板结构压电主-被动控系 统的研究[D].南京：南京航空航天大学，2012.

[7]崔海涛.压电智能悬臂梁的被动与主动振动控 制研究[D].西安：西北工业大学，2004.

[8]CHENG C C，LIN C C. An impedance approach for determining optimal locations and shapes of multiple induced strain actuators[J]. Smart Mater struct，2005，14（6）：112-126.

[9]贺江平，钟发春.基于压电效应的减振技术和 阻尼材料[J].振动与冲击，2005，24（4）：9-13.

[10]熊诗波，黄长艺.机械工程测试技术基础[M]. 北京：机械工业出版社，2009：15-159.

（责任编辑：李丽）