基于DNA链置换的分子逻辑门计算模型

张文逸++殷志祥

摘要：DNA计算是近年来的研究热点，分子逻辑门是DNA计算机体系结构和运算实现的重要基础。将DNA自组装与链置换技术和荧光标记相结合，在现有的链置换逻辑计算模型的基础上，构造了非门，与门，与非门，或门和或非门。可在室温下进行，减少了因复杂的生物操作步骤带来的误差。使用荧光检测来判断逻辑结果，操作简单，容易检测，且灵敏度高。

关键词：DNA计算；自组装；链置换；荧光标记；逻辑门

中图分类号：TP301.6 文献标志码：A

文章编号：1672-1098（2015）01-0007-04

自从1946年科学家发明了第一台电子计算机ENIAC，计算机迅猛发展并时刻影响着人类的生活。但随着科技的进步，传统计算机已无法满足呈指数增长的大规模运算需求，加之“Moore定律”导致的芯片研究成本和半导体物理极限，集成电路的时代不可能永远下去。美国物理学家Feynman于1959年首次提出了分子计算机的思想[1]。20世纪90年代，美国加州大学的Leonard Adleman于1994年第一次在试管中通过利用寡核苷酸链进行实验，解决了经典的有向Hamilton路问题[2]，首次从实验上证明了分子计算机的可行性。

分子逻辑门是实现分子计算机的基础。文献[3]首次提出布尔逻辑分子计算机模型，这是使用DNA分子模拟布尔电路终将实现以DNA为核心的分子计算机。文献[4]构建了DNA核酸分子逻辑非门、与门和异或门，文献[5]利用DNA核酶构建了多种DNA逻辑运算模型，文献[6]构建了半加器的复杂逻辑门，文献[7]首次构建了逻辑与门、与非门和禁门，文献[8]构建了一套完整的无酶逻辑电路，文献[9]构建了环状DNA逻辑门，文献[10]使用多种DNA酶构建逻辑运算模型。

近年来，DNA计算发展迅速[11]，融合了荧光标记、链置换、自组装和纳米颗粒[12]等多种分子操作技术。其中，结合荧光标记的DNA链置换技术更是因在Science和Nature等杂志[13-15]上发表的工作而具有广泛的应用前景。本文在文献[16]的基础上，结合荧光标记技术[17-18]，改进并构造了基本的逻辑门单元，以寡核苷酸链作为输入信号，荧光检测作为输出信号，能在室温下自发进行，对结果有更好的可读性。

1DNA自组装和链置换

11DNA自组装

DNA自组装是指一些带有输入信息的DNA分子根据碱基互补配对原则，在一定的温度、浓度、酸碱度以及特定酶的作用下，自组装生成带有输出信息的新的DNA分子的过程。自组装计算模型是通过DNA分子间的相互作用形成特定的构型来完成计算过程，是由Winfree等首次提出来的一种DNA计算模型[19-21]。文献[22]首先使用复杂DNA自组装结构实现了简单的逻辑运算。文献[23]将自组装DNA计算的基本思想用于求解布尔逻辑表达式并将其实现逻辑电路。该模型目前在生物计算中得到了良好的应用。

12链置换技术

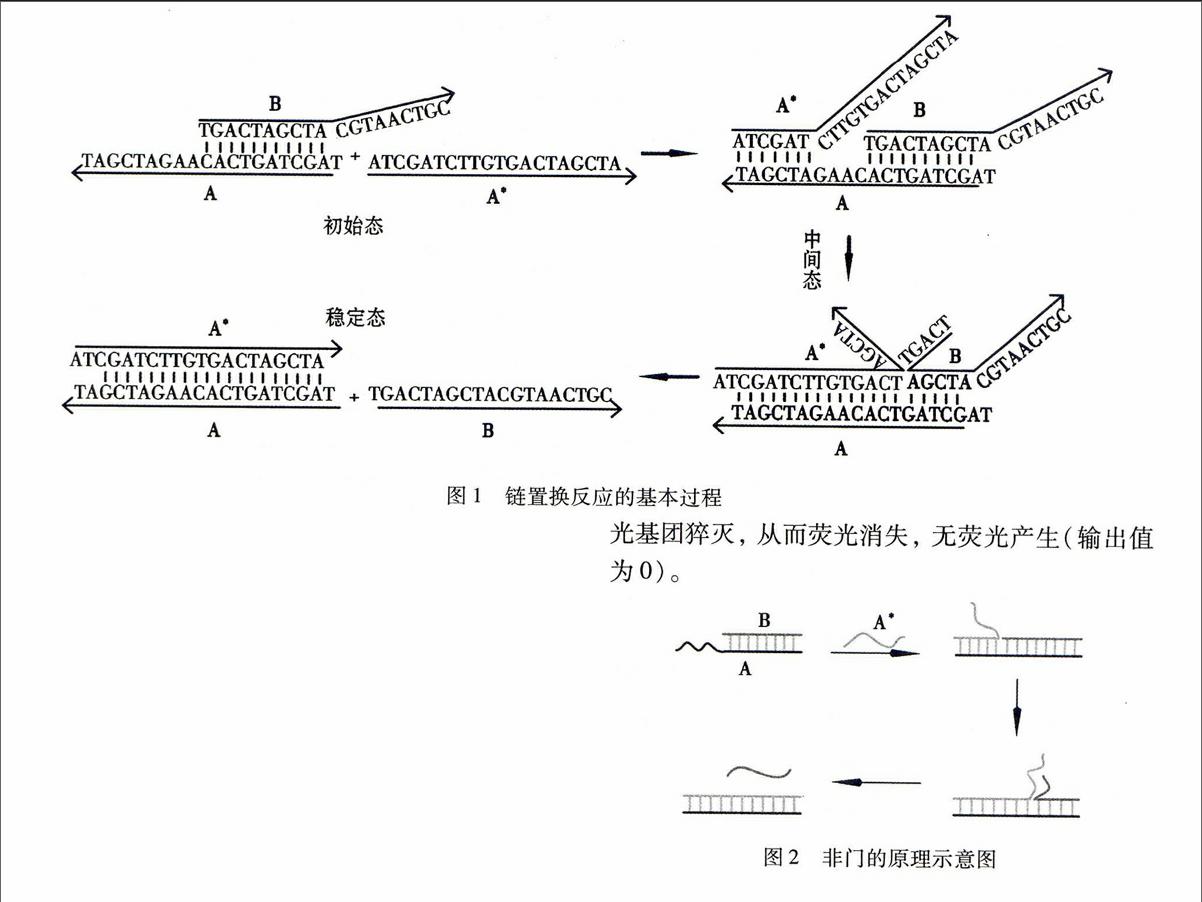
链置换技术是利用分子杂交系统趋向稳定能级的特点，通过加入不同长度和序列的输入链来诱导控制链置换反应，从而释放另一条DNA链的过程。DNA链置换的基本原理如图1所示。链A/B是由两条部分互补的DNA链结合成的部分双链，单链部分在反应中被称作立足点，发生链置换反应的可能性随立足点的增长而增大，链A*是序列与A完全互补的单链。单链A*先特异性识别结合立足点，为达到最稳态分支开始迁移，A*与A的碱基对逐渐取代B与A的碱基对，直至完全置换释放出B链。该反应过程具有自引发性，灵敏性和准确性等特点，近年来发展迅速，已成为分子计算领域的研究热点。

图1链置换反应的基本过程

2链置换逻辑门的计算模型

21非门

在反应底物自组装结构的部分双链中长链A的5′端标记荧光基团FAM，与A链完全互补的单链DNA链A*的5′端标记荧光猝灭基团DABCYL， 当无DNA链输入（输入值为0）时， 有荧光产生（输出值为1）；当加入互补链A*（输入值为1）时， 因A链与A*链完全互补结合， 荧光猝灭基团将荧光基团猝灭， 从而荧光消失， 无荧光产生（输出值为0）。

图2非门的原理示意图

22与门

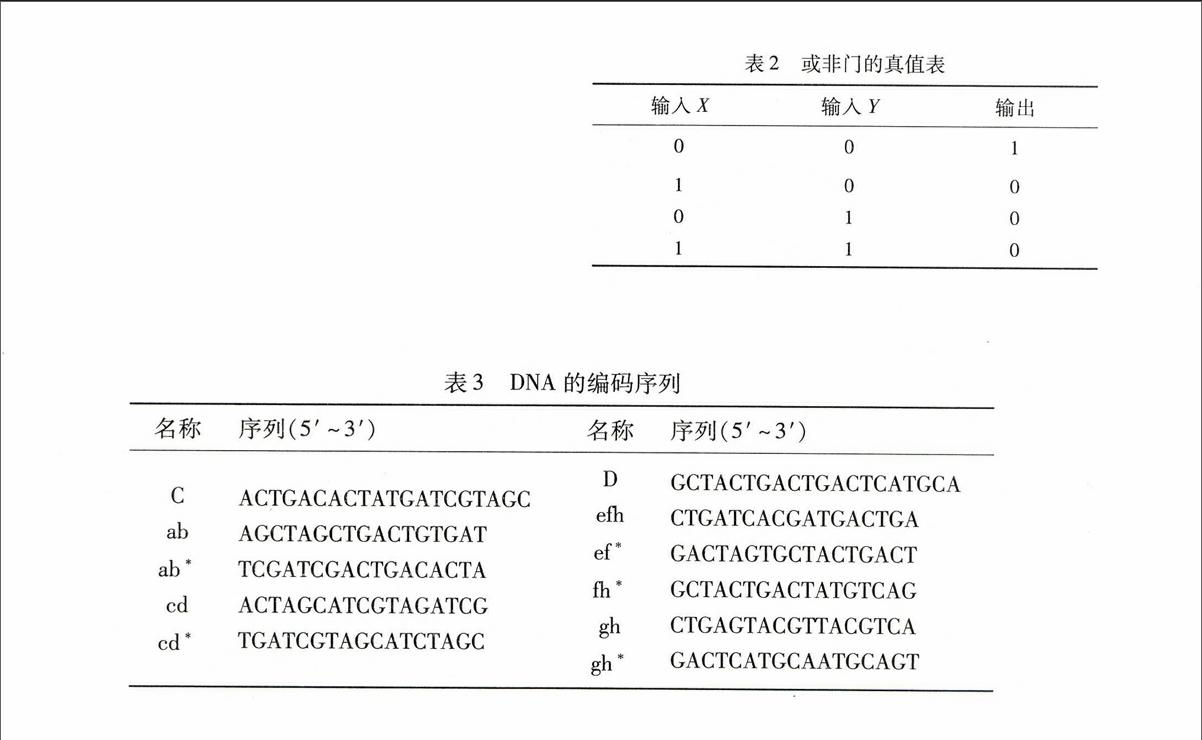
反应底物自组装结构由主链C和单侧信号识别链ab、cd杂交而成，主链C长20 bp，分为左右各长10 bp的碱基片断，信号识别链由长10 bp的结构区域b、c和长约6～7 bp的特异性识别位点a、b组成，输入链ab*和cd*为分别与ab和cd完全互补的信号链。对所需要的DNA序列进行编码后，在主链C的5′和3′端分别标记荧光基团FAM和ROX，在b的5′端和c的3′端分别标记荧光猝灭基团DABCYL。定义同时有两种不同的荧光产生时为输出1，否则为输出0。

当无信号输入（0，0）时，自组装结构无变化，无荧光产生（输出值为0）；当输入信号1（1，0）时，ab*将ab完全置换，产生FAM荧光，但无ROX荧光（输出值为0）；当输入信号2（0，1）时，cd*将cd完全置换，产生ROX荧光，但无FAM荧光（输出值为0）；当同时输入信号1和2（1，1）时，ab*将ab完全置换，产生FAM荧光，cd*将cd完全置换，产生ROX荧光（输出值为1）。

23与非门

自组装结构同与门相同（见图3），对所需要的DNA序列进行编码后，在主链C的5′和3′端分别标记荧光基团FAM和ROX，在输入链ab*中b*的5′端和cd*中c*的3′端分别标记荧光猝灭基团DABCYL。有荧光产生时为输出1，无荧光则为0（见表1）。

图3与门的原理示意图

当无信号输入（0，0）时，自组装结构无变化，有荧光FAM和ROX产生（输出值为1）；当输入信号1（1，0）时，ab*将ab完全置换，荧光猝灭基团将荧光FAM基团猝灭，FAM荧光消失，但有ROX荧光（输出值为1）；当输入信号2（0，1）时，cd*将cd完全置换，荧光猝灭基团将荧光ROX基团猝灭，ROX荧光消失，但有FAM荧光（输出值为1）；当同时输入信号1和2（1，1）时，ab*将ab完全置换， FAM荧光消失，cd*将cd完全置换，ROX荧光消失，无荧光（输出值为0）。endprint

表1与非门的真值表

输入X输入Y输出

001

101011110

24或门

反应底物自组装结构由主链D和多信号识别区域（e，f，g，h）组成。单种输入为混合输入信号，信号3为输入链（ef*，gh*），信号4为输入链（fh*，gh*）。对所需要的DNA序列进行编码后，在主链B的中间部位和3′端分别标记荧光基团FAM和ROX，在efh中f和gh中g的3′端分别标记荧光猝灭基团DABCYL。定义同时有两种不同的荧光产生时为输出1，无荧光为输出0。

当无信号输入（0，0）时，自组装结构无变化，无荧光产生（输出值为0）；当输入信号3（1，0）时，ef*将efh置换成部分双链，产生FAM荧光，gh*将gh完全置换，产生ROX荧光（输出值为1）；当输入信号4（0，1）时，fh*将efh置换成部分双链，产生FAM荧光，gh*将gh完全置换，产生ROX荧光（输出值为1）；当同时输入信号3和4（1，1）时，ef*和fh*将efh置换成部分双链，产生FAM荧光，gh*将gh完全置换，产生ROX荧光（输出值为1）。

25或非门

自组装结构同或门相同（见图4），对所需要的DNA序列进行编码后，在主链D的中间部位和3′端分别标记荧光基团FAM和ROX，在ef*的5′端、fh*中f和gh*中g的3′端分别标记荧光猝灭基团DABCYL。定义同时有两种不同的荧光产生时为输出1，否则为输出0（见表2）。

图4或门的原理示意图

当无信号输入（0，0）时，自组装结构无变化，有荧光FAM和ROX（输出值为1）；当输入信号3（1，0）时，ef*将efh置换成部分双链，荧光猝灭基团将荧光FAM基团猝灭，FAM荧光消失，gh*将gh完全置换，荧光猝灭基团将荧光ROX基团猝灭，ROX荧光消失（输出值为0）；当输入信号4（0，1）时，fh*将efh置换成部分双链，荧光猝灭基团将荧光FAM基团猝灭，FAM荧光消失，gh*将gh完全置换，荧光猝灭基团将荧光ROX基团猝灭，ROX荧光消失（输出值为0）；当同时输入信号3和4（1，1）时，ef*和fh*将efh置换成部分双链，荧光猝灭基团将荧光FAM基团猝灭，FAM荧光消失，gh*将gh完全置换，荧光猝灭基团将荧光ROX基团猝灭，ROX荧光消失（输出值为0）（见表3）。

表2或非门的真值表

输入X输入Y输出

001

101011000

表3DNA的编码序列

名称序列（5′～3′）名称序列（5′～3′）

Cabab*cdcd*ACTGACACTATGATCGTAGC

AGCTAGCTGACTGTGATTCGATCGACTGACACTA

ACTAGCATCGTAGATCGTGATCGTAGCATCTAGCDefhef*fh*ghgh*

GCTACTGACTGACTCATGCACTGATCACGATGACTGA

GACTAGTGCTACTGACTGCTACTGACTATGTCAG

CTGAGTACGTTACGTCAGACTCATGCAATGCAGT

3结论

本文以现有的链置换逻辑计算模型为基础，结合荧光标记技术，用荧光检测作为输出信号，并对输入信号进行相应的标记，实现了非门，与门，与非门，或门和或非门的逻辑门操作。该逻辑门可在室温下自发反应，减小了实验误差。在读取逻辑结果时，通过荧光的出现情况来判断逻辑真值，操作简单，容易检测，且灵敏度高。但是对于不同的逻辑门，需要对自组装结构进行不同的设计，且在实验过程中，复杂体系的DNA序列设计难度增加，可能会出现碱基错配的现象，需要进一步进行实验验证和改进。

参考文献：

[1]FEYNMAN R P. Miniaturization[J]. Reinhold， 1961： 282-296.

[2]ADLEMAN L M. Molecular computation of solutions to combinatorial problems[J].Science，1994，266（5 187）：1 021-1 024.

[3]OGIHARA M，RAY A.Simulating Boolean circuits on a DNA computer[J].Algorithmica 1999，25（2-3）：239-250.

[4]STOJANOVIC MN，MITCHELL TE，STEFANOVIC D.Deoxyribozyme based logic gates[J]. Am Chem Soc，2002， 124（14）：3 555-3 561.

[5]MILLIAN N S，DARKO S.A deoxyribozyme-based molecular automaton[J]. Nat Biotechnol， 2003，21：1 069-1 074.

[6]STOJANOVIC MN，STEFANOVIC D. Deoxyribozyme based half-adder[J]. Am Chem Soc，2003，125（22）：6 673-6 676.

[7]SAGHATELIAN A，VOLCKER NH，GUCKIAN KM，et al. DNA-based photonic logic gates： AND，NAND，and INHIBIT[J].Am Chem Soc，2003，125（2）：346-347.

[8]SEELIG G，SOLOVEICHIK D，ZHANG DY，et al. Enzyme-free nucleic acid logic circuits[J].Science，2006，314：1 585-1 588.

[9]ZHANG C，YANG J，XU J.Circular DNA logic gates with strand displacement[J].Langmuir，2010， 26（3）：1 416-1 419.

[10]ELBAZ J，LIOUBASHEVSKI O，WANG F，et al. DNA computing circuits using libraries of DNAzyme subunits[J]. Nat Biotechnol， 2010， 5： 417-422.

[11]万菲，董晨，杨静，等. DNA 计算技术的发展与应用[J].中国科学院院刊，2014，29（1）：94-105.endprint