一种考虑吸引型异常事件的行人元胞自动机模型

陈艳艳，陈宁，王杨，冯国臣

（北京工业大学城市交通学院，北京100124）

一种考虑吸引型异常事件的行人元胞自动机模型

陈艳艳*，陈宁，王杨，冯国臣

（北京工业大学城市交通学院，北京100124）

鉴于目前行人元胞自动机仿真研究中对于吸引型异常事件情况下模型的缺失，本文提出了一种特殊的考虑吸引型异常事件的行人元胞自动机模型.当异常事件发生后，模型将行人分为漠视、驻足、围观和围观离开四种类型.漠视类型指对异常事件毫无兴趣，不受异常事件影响的行人，其动力特性与行人在正常情况下的动力特性一致；驻足类型指对异常事件较有兴趣，驻足观看的行人，其动力特性由能使行人在原地停留的驻足效用值决定；围观类型指对异常事件极有兴趣，向异常事件中心靠近围观的行人，其动力特性由围观效用决定；围观离开类型指对异常事件失去兴趣，从围观人群离开的行人，其动力特性由围观离开效用决定.仿真效果显示，该模型基本可反映行人聚集围观的表征和内部特性.

交通工程；仿真模型；元胞自动机；行人

1 引言

由于受个体行为的直接影响，相较于机动车交通流而言，行人交通流更为复杂，很难用简单的数学公式进行描述，这也就使得越来越多的研究者们开始采用计算机仿真的方式来进行行人交通流特性的研究.在行人交通流仿真研究过程中陆续出现了许多微观行人仿真模型，最为典型的包括社会力模型、格子气模型和元胞自动机模型，近年来，元胞自动机模型引起了越来越多研究者的注意.元胞自动机模型是一种离散模型，它通过模拟行人的个体行为，并通过行人微观行为之间的相互影响作用，呈现系统的整体宏观行为特征[1].

目前，元胞自动机模型已被广泛地应用于行人交通流仿真系统的研究中，根据应用环境的差别，现有的行人元胞自动机模型可分为两类：正常情况下的行人元胞自动机模型和疏散情况下的行人元胞自动机模型.对于正常情况下的行人元胞自动机模型，Victor JBlue、Andreas Schadschneider、C Burstedde、岳昊等[1-5]对此进行了深入的研究，研究内容集中于行人元胞规则集的定义及群体效应、自组织性等行人宏观特性的显现；对于疏散情况下的行人元胞自动机模型，Dirk Helbing、Ansgar Kirchner、Kazuhiro Yamamoto等[6-8]对此进行了深入的研究，研究内容集中于出口处拱形区域、“快即是慢”等疏散特性的实现.在目前的行人元胞自动机模型研究中，欠缺一种考虑吸引型异常事件的元胞自动机模型，吸引型异常事件即对周边行人产生吸引作用的异常事件，如摆卖货品、乞讨卖艺等，在发生吸引型异常事件时，往往会造成人群的围观聚集，形成拥挤，影响系统的交通流特性.鉴于此，本文提出了一种考虑吸引型异常事件的行人元胞自动机模型，以提供一种行人异常事件交通特性研究的新型工具.

2 模型

本文所提出的模型针对于客运枢纽单向人行通道，该模型是由W⋅H个大小相等的元胞组成的二维离散系统如图1所示.

图1 人行通道系统示意图Fig.1 The simulation system

该系统中共有3种元胞类型：墙元胞、空元胞和行人元胞.墙元胞代表人行通道的墙壁，其不可被行人元胞占用；空元胞代表人行通道中的空旷区域，其可以被行人元胞占用；行人元胞代表人行通道中的行人，其可以占用周围邻域的空元胞，系统中设定的行人元胞运动方向为从左至右.据Navin等人[9]的研究成果，系统中定义元胞的大小为一个0.25m2的正方形方格、行人元胞的运动速度为1.25m/s、系统的时间步长为0.4 s.

该模型分两种情况：正常情况和非正常情况，正常情况指通道内未发生吸引型异常事件的情况，非正常情况指通道内发生了吸引型异常事件的情况.不管在正常还是非正常情况下，行人元胞都只能向自身和周围邻域的八个元胞运动，具体的运动方向由效用值决定.

2.1 正常情况

行人元胞与其邻域的八个元胞组成一个3×3的运动场元胞矩阵，矩阵中九个元胞对行人元胞均有一定的吸引程度，吸引程度的大小由效用值决定，效用值越大，吸引程度越大，正常情况下，元胞效用值的计算采用岳昊[5]等人设计的元胞效用值计算方法，即元胞效用值是方向参数效用、空格参数效用和前进参数效用三个参数效用值之和.

方向参数代表了行人元胞向目的地运动的意向，如式（1）所示.

式中Dij为横坐标为i，纵坐标为j的元胞的方向参数效用值；P0,-1,…,P0,1为Dij相对于行人元胞的位置，如图2所示.

空格参数代表了行人元胞向不被占用的元胞运动的意向，如式（2）所示.

式中Eij为横坐标为i，纵坐标为j的元胞的空格参数效用值.

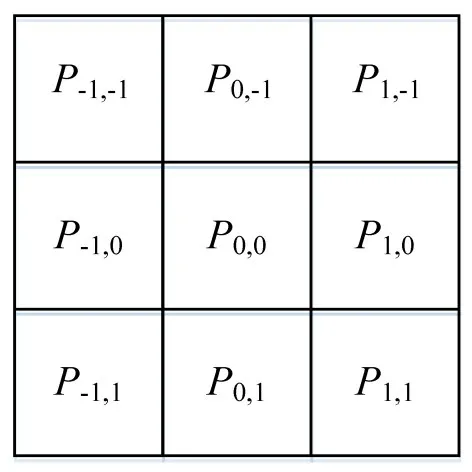
图2 行人元胞的邻域元胞Fig.2 Theneighboring cellsofpedestrian cell

前进参数代表了行人元胞向空旷区域运动的意向，如式（3）所示.

式中Fij为横坐标为i，纵坐标为j的元胞的前进参数效用值；S1为视野感知区域的空元胞数；S2为视野感知区域被占用的元胞数；15为元胞不与边界元胞相邻时元胞感知区域的元胞总数；10为元胞与边界元胞相邻时元胞感知区域的元胞总数.

2.2 非正常情况

吸引型异常事件是指会对周边行人产生吸引效用的异常事件，如摆卖货品、吵闹打架、伤病跌倒等行为，行人对吸引型异常事件的反应过程如图3所示.

图3 行人对异常事件的反应过程Fig.3 The processofpedestrians’reaction to an attractive incident

行人能否发现异常事件取决于异常事件及其所形成的围观人群是否处于行人的视野范围内，根据杨玉想等的研究成果[10]，行人的动态视野为6.94m，视角范围为40°–120°，鉴于此，本文模型中设定行人的视距7m，视角90°，周边视力沿中心线方向逐步递减，如图4所示.当异常事件首次出现在行人元胞视野中时，行人元胞会以一定概率被标记为围观、驻足或漠视类型，当围观类型行人元胞对异常事件失去兴趣后，其有可能转变成围观离开类型，四种类型对应了四种不同的效用值计算方法.

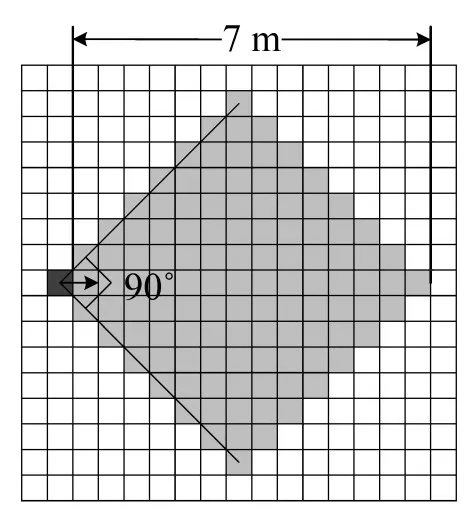
图4 行人视野范围Fig.4 The pedestrians’visual fiel

2.2.1 漠视

当行人元胞类型被标记为漠视时，行人元胞运动场中各元胞效用值的计算与正常情况下元胞效用值的计算方法相同，此处不再赘述.

2.2.2 驻足

标记为驻足类型的行人元胞代表对异常事件有一定兴趣行人，其在发现异常事件后，采取的行为为在原地观望，当了解了自己所希望获取的信息或彻底对异常事件丧失兴趣后，他们离开异常事件的吸引范围区域，继续向目的地行进.在本文模型中，当行人元胞被标记为驻足类型时，行人元胞的驻足属性被赋予一个随机数值SR，代表行人的停驻时间，在每个时间步长，SR值减1，当SR值小于0时，则行人元胞被取消标记为驻足类型，恢复为正常情况.在行人元胞被标记为驻足类型期间，运动场中元胞的效用值由归一化的驻足效用Sij决定，为使被标记为驻足类型的行人元胞停留在原地，处于运动场中心位置元胞的驻足效用被赋予一个奖励值SA，其它元胞的驻足效用值为0.驻足效用的计算流程和计算公式如图5和式（4）所示.

为统一量纲，需对驻足效用进行归一化处理：运动场矩阵中9个元胞的驻足效用值按数值从大到小排序，最大赋值9，最小赋值1，由此得归一化效用值Sij.

图5 驻足效用计算流程图Fig.5 The processesofdetermining stopped utility

2.2.3 围观

标记为围观类型的行人元胞代表对异常事件具有强烈兴趣的行人，其在发现异常事件后，采取的行为为接近异常事件的发生位置，了解异常事件的详细信息，在对信息失去兴趣或处置完异常事件后，离开异常事件的吸引范围区域，继续向目的地行进.在本文模型中，当行人元胞被标记为围观类型时，行人的围观属性被赋予一个随机数值CR，代表行人的围观时间，在每个时间步长，CR值减1，当CR值小于0时，则行人元胞被取消标记为围观类型，恢复为正常情况或被标记为围观离开类型.在行人元胞被标记为围观类型期间，运动场中元胞的效用值由归一化的围观效用Cij决定，Cij是归一化的异常事件吸引效用归一化的围观人群外圈最近空隙吸引效用和空格参数效用Eij三者之和，如式（5）所示.异常事件吸引效用的大小与元胞距异常事件的距离呈反比，代表了异常事件对行人的吸引作用，但当元胞的距离小于2倍的元胞边长时，被置0，代表了异常事件与行人间的最小安全距离，异常事件吸引效用值计算公式如式（6）所示，归一化后得围观人群外圈最近空隙吸引效用的大小与元胞距围观人群外圈最近元胞的距离呈反比，如图6所示，运动场中越靠近围观人群外圈最近元胞的元胞，其效用值越大，代表了围观人群外围空隙对行人元胞的吸引作用，围观人群外圈最近空隙吸引效用计算公式如式（7）所示，归一化后得空格参数效用Eij代表了行人元胞向不被占用元胞行走的意愿，计算公式如式（2）所示.

图6 围观人群外圈最近元胞Fig.6 The schematic diagram of the Cellij'souternearest empty cell

式中Cij为围观效用值为归一化的异常事

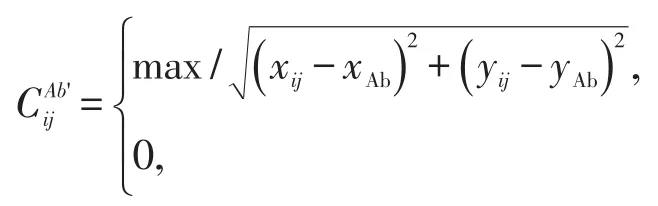
2.2.4 围观离开

当围观类型行人元胞对异常事件失去兴趣后，其将离开异常事件吸引区域，继续向原始目的地行进.在本文模型中，当CR值小于0时，行人元胞将由围观类型变为围观离开类型或漠视类型.当行人元胞的邻域均为围观类型行人元胞或异常事件元胞时，其变为围观离开类型，当行人元胞的邻域并非均为围观类型行人元胞或异常事件元胞时，其变为漠视类型，如图7所示.围观离开型行人元胞效用值受异常事件排斥力影响，代表其在失去兴趣后期望离开异常事件影响区域，同时，在其运动场矩阵中，其可与已被占用的元胞交换位置，代表其离开围观人群的过程.

图7 围观类型转变示意图Fig.7 The schematic diagram of the changing process from the circusee pedestrians to circusee-leave type orunaffected type

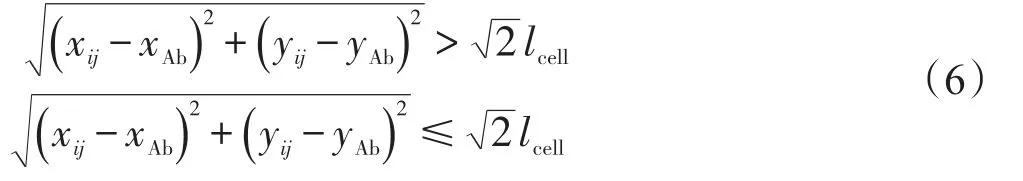
化的离开距离效用和归一化的离开直线效用加和求得如式(8)所示.离开距离效用与元胞距异常事件中心的距离成正比，距离越大，效用值也越大如式(9)所示；离开直线效用与行人元胞、异常事件元胞及运动场内目标元胞的夹角呈反比，夹角越小，效用值越大如式(10)所示，围观离开效用使行人元胞以最快速度离开围观人群.

围观和围观离开类型行人元胞的动力性受异常事件吸引的影响，表现为受到吸引、接近异常事件位置、围观、离开异常事件位置和继续向目的地行进等一系列过程，其具体流程如图8所示.

3 仿真和效果

正常情况下的行人交通流特性岳昊[5]等人已经进行了反复测试，本文不再赘述.目前，在行人交通领域研究中，对吸引型异常事件情况下的行人交通特性的研究较少，现有的研究集中于社会心理学和管理学领域，近年来，由于群体事件的增多，一些计算机仿真领域的研究者开始对其进行研究，得出了聚集人群的部分特征属性[11-13].本文采用表征特征分析和内部特征分析的方法对本文所提出的模型进行了有效性验证.

图8 围观和围观离开效用计算流程Fig.8 The processesused to determine circusee utility and circusee-leave utility

针对于不同类型的异常事件，行人类型的比例及相关参数也不尽相同，为了解行人对不同类型异常事件的反应效果，本文采用问卷调研的形式于2014年7月2–4日在北京地铁西单站进行了通道内行人受异常事件吸引调查实验.实验共发放问卷106份，回收有效问卷102份，性别比例为男性51%，女性49%，年龄区段20–24岁为22%，25–29岁为49%，30–39岁为23%，40岁以上为6%，具体调研结果如表1所示.

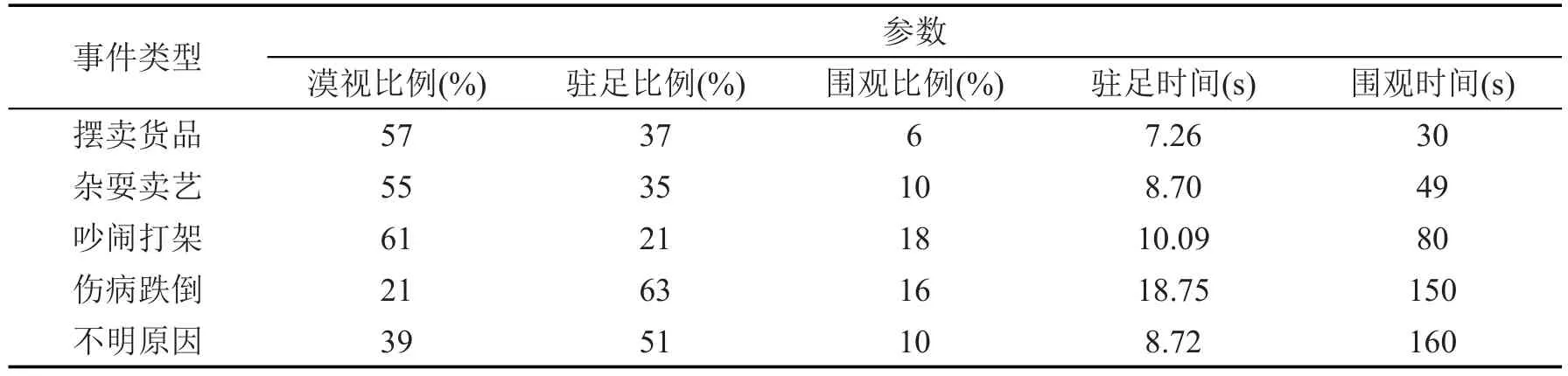
表1 行人受异常事件吸引调研参数统计表Table 1 The parameters of pedestrians who are attracted by attractive incidents

当发生吸引型异常事件（吵闹打架）时，漠视、驻足和围观三种类型行人的比例分别为61%、21%和18%，驻足类型行人的驻足平均时间为10 s，围观类型行人的围观平均时间为80 s，通道宽度为8m，仿真系统依此参数进行设计.系统的输入为西单站11:00–12:00时间段内通道实际客流产生量.仿真实验效果如图9所示.

在仿真场景中（图9），异常事件发生约200帧（80 s）后，以异常事件发生点为圆心，形成一个中心真空，外围人群环绕的圆形围观人群聚集圈；在实际场景中（图10），围观人群主要有以下几个特征：

（a）围观人群的中央为吸引型异常事件源，是吸引周围行人围观的原动力，如图9中实线圈所示范围；

（b）紧邻事件源的周边为一空白区域，受异常事件的影响，围观人群不会进入这片区域，如图10中虚线圈所示范围；

（c）围观人群最外圈是对异常事件具有较强的兴趣而围着观看的人群，如图9中点划线所示范围.

图9 异常事件下仿真效果图（第1至800帧）Fig.9 The snapshotsofsimulation underattractive incidents (from 1th frame to 800 th frame)

图10 围观人群实景图Fig.10 Live-picturesof the circusee crowd

可以看出，实际场景中的三个特征与仿真实验200帧后所形成的以异常事件为圆心，中心真空，外围人群环绕的围观人群聚集圈基本一致，可见，从表征特征上来说，本文模型可基本反映吸引型异常事件发生后行人的宏观交通流特性.

本文通过对模型中系统输入率和最大聚集人数、达到最大聚集人数时间关系的分析，验证本文所提出模型的内部交通流特性.仿真系统静态模型与上文所述相同，通道系统的客流产生率从5%到35%逐步递增，实验结果如图11和图12所示.

图11 最大聚集人数和系统输入率关系图Fig.11 The plotof the relationship between themax of crowd numberand the enter rate

图12 不同输入率情况下聚集人数与系统时间关系图Fig.12 The plotofcrowd gathering number

如图11所示，在仿真系统中，在最大聚集人数达到平衡点（约60人）前，最大聚集人数随系统输入率的增加而增加，当达到平衡点后，最大聚集人数不再随系统输入率的增加而变化，即当系统输入率超过20%后，最大聚集人数稳定维持在约60人左右的水平.如图12所示，在仿真系统中，达到最大聚集人数的时间与系统输入率相关，在最大聚集人数达到平衡点前，达到最大聚集人数的时间随系统输入率的增加而增加，如系统输入率为15%时，其达到最大聚集人数的时间（第245帧）要小于系统输入率为10%时达到最大聚集人数的时间（308帧）.当达到最大聚集人数平衡点（约60人）后，达到最大聚集人数的时间不再随系统输入率的增加而变化，稳定维持在约211帧左右的范围.本文所得出的结论与殷雁君[11]和常钦[12,13]所归纳出的行人聚集特征属性基本一致，可见，从行人聚集的内部特征上来说，本文模型亦可基本反映吸引型异常事件发生后行人受异常事件吸引集聚的交通流特性.

4 研究结论

鉴于目前行人元胞自动机研究中对于吸引型异常事件情况下模型的缺失，本文构建了一种考虑吸引型异常事件的行人元胞自动机模型，并对模型的有效性进行了验证，得出结论如下：

(1)发生吸引型异常事件情况下，模型中将行人元胞分为漠视、驻足、围观和围观离开四种类型，漠视型行人元胞的效用值计算方法与正常情况下行人的效用值计算方法一致[5]，驻足型行人元胞的效用值由驻足效用决定，围观型行人元胞的效用值由空格效用、异常事件吸引效用及外圈最近空隙吸引效用决定，当围观行人离开围观人群时，其会转变成围观离开类型，效用值由离开直线效用和离开距离效用决定.

(2)从表征特征上验证了吸引型异常事件发生后本文模型的仿真效果.当异常事件发生后，仿真结果显示，行人会形成一个以异常事件为圆心，中心真空，外围人群环绕的围观人群聚集圈，这与实际场景中所呈现的行人聚集情况基本一致.

(3)从内部特征上验证了吸引型异常事件发生后本文模型的仿真效果.当异常事件发生后，仿真结果显示行人聚集的特征为：

①在最大聚集人数达到平衡点前，最大聚集人数随系统输入率的增大而增大，达到平衡点后，最大聚集人数基本保持不变；

②在最大聚集人数达到平衡点前，系统输入率越大，达到最大聚集人数的时间越快，达到平衡点后，达到最大聚集人数的时间基本保持不变.

这与目前研究成果中行人聚集特性基本一致.

[1]Blue V J,Adler JL.Cellular automatamicrosimulation for modeling bi-directional pedestrian walkways[J]. Transportation Research Part B-Methodological,2001, 35(3):293-312.

[2]Burstedde C,et al.Simulation of pedestrian dynamics using a two-dimensional cellular automaton[J].Physica A,2001,295(2001):507-525.

[3]Schadschneider A.Cellular automaton approach to pedestrian dynamics-theory[J].Springer,2001:75-85.

[4]Blue V J,Adler J L.Emergent fundamental pedestrian flows from cellular automatamicrosimulation[J].Traffic Flow Theory,1998(1644):29-36.

[5]Yue H,et al.Simulation of pedestrian flow on square lattice based on cellular automatamodel[J].Physica AStatistical Mechanics and ITS Applications,2007,384 (2):567-588.

[6]Kirchner A,Nishinari K,Schadschneider A.Friction effects and clogging in a cellular automaton model for pedestrian dynamics[J].Physical Review E,2003,67(5): 1-12.

[7]Helbing D,Farkas I,Vicsek T.Simulating dynamical features of escape panic[J].Nature,2000,407(6803): 487-490.

[8]Yamamoto K,Kokubo S,Nishinari K.Simulation for pedestrian dynamics by real-coded cellular automata (RCA)[J].Physica A-Statistical Mechanics and ITS Applications,2007,379(2):654-660.

[9]Navin F.Bicycle traffic flow characteristicsexperimental results and comparisons[J].ITE Journal-Institute of Transportation Engineers,1994,64(3):31-36.

[10]杨玉想,赵春斌.视觉特性：道路绿地景观设计的基础因素[J].中国园艺文摘,2009(3):54-55.[YANG Y X,ZHAO C B.Visual characteristic:Fundamental factors of road green space landscape design[J].Chinese Horticulture Abstracts,2009(3):54-55.]

[11]殷雁君,唐卫清.好奇心理的人群聚集行为仿真[J].智能系统学报,2014,9(4):413-418.[YIN Y J,TANGW Q.Simulation of the crowd collective behavior based on curiosity[J].Transactions on Intelligent Systems,2014,9 (4):413-418.]

[12]常钦.基于Agent的群体性事件动力学模型研究[J].中国人民公安大学学报(自然科学版),2010(4):83-86. [CHANG Q.Research of dynamics model of mass incidents based on Agent[J].Journal of Chinese People's Public Security University:Science And Technology,2010(4):83-86.]

[13]常钦,党会森.基于网格Agent的群体性事件人群聚集模型研究[J].中国人民公安大学学报(自然科学版), 2011,69(3):71-74.[CHANG Q,DANG H S.Research of crowds gathered model of mass incidents based on grid Agent[J].Journal of Chinese People's Public Security University:Science and Technology,2011,69 (3):71-74.]

A Cellu lar Autom ata Model Considering A ttractive Incidents

CHEN Yan-yan,CHEN Ning,WANGYang,FENGGuo-chen
(The CollegeofMetropolitan Transportation,Beijing University of Technology,Beijing 100124,China)

Due to the lack ofmodelling pedestrian behaviors under the incidents that attract pedestrians, this paper proposes a new cellular automaton model aim ing to reproduce the behaviors induced by such attractive incidents.When attractive incidents occur,the proposed model w ill classify the pedestrians into four groups:unaffected,stopped and circusee(i.e.surround and watch)and circusee-leave pedestrians.The dynamics of unaffected type is same as that under normal circumstances.The stopped type represents the pedestrian is somewhat interested in the attractive incident.Its dynamics is determ ined by stopped utility which canmake the pedestrian stop for awhile.The circusee type represents pedestrianswho show strong interest in the attractive incidents and are intended tomove closer to the venue and gainmore know ledge.Its dynam ics is determ ined by circusee utility.The circusee-leave type represents the pedestrian that loses interest and wants to leave the crowd.Its dynamics is determined by circusee-leave utility.The simulation results demonstrate that the proposed model can reflect the surface and internal characteristic of pedestrian gathering.

traffic engineering;simulationmodel;cellularautomata;pedestrian

1009-6744（2015）03-0056-08

U495

A

2014-10-29

2015-01-13录用日期：2015-01-19

交通运输部重大科技专项（2012-364-220-109）.

陈艳艳（1970-），女，河南人，教授.＊通信作者：cdyan@bjut.edu.cn