拉/剪载荷下橡胶材料的Mullins诱导各向异性研究

李飞，丁智平，卜继玲，黄友剑

（1.湖南工业大学 机械工程学院，湖南 株洲412007；2. 株洲时代新材料科技股份有限公司，湖南 株洲412007）

拉/剪载荷下橡胶材料的Mullins诱导各向异性研究

李飞1，2，丁智平1，卜继玲2，黄友剑2

（1.湖南工业大学 机械工程学院，湖南 株洲412007；2. 株洲时代新材料科技股份有限公司，湖南 株洲412007）

使用矩形橡胶试样依次进行不同位移载荷水平下纯剪切和轴向拉伸/纯剪切试验，研究橡胶材料在拉/剪载荷作用下的Mullins软化诱导各向异性。试验结果表明，橡胶纯剪切试样在经过轴向拉伸后，由于Mullins软化诱导各向异性的影响，再进行纯剪切试验会使试样的横向刚度增大。利用试样的轴向拉伸/纯剪切试验数据，拟合得到相应的Mullins软化控制参数，反映Mullins软化诱导各向异性对剪切试样横向刚度的影响。分别对纯剪切试样在2种试验载荷作用下的横向刚度曲线进行有限元数值模拟，仿真估计值与试验值的残差平方和均值的对比结果表明，考虑Mullins软化诱导各向异性可以显著提高拉-剪载荷作用下橡胶元件横向剪切刚度的预测精度。

橡胶；纯剪切；Mullins软化；诱导各向异性；有限元；刚度

0 引言

橡胶作为一种独特的弹性阻尼材料而被广泛地应用于各种隔振系统中[1]，其在承载过程中不仅承受很大的轴向载荷，同时还受到横向剪切载荷作用，产生较大的剪切变形，例如轴箱弹簧、旁承和锥形簧等。为了确保橡胶弹性元件的使用性能，对其在剪切载荷作用下的横向刚度的设计和预测，就显得非常重要。

橡胶受载变形后会发生Mullins软化效应，且这种软化效应具有诱导各向异性。这是因为橡胶材料在拉伸过程中各个方向发生了不均匀的软化，所以产生了各向异性[2]，且橡胶承受的载荷愈大，Mullins软化诱导各向异性愈加显著。利用有限元软件对橡胶弹性元件的刚度进行数值模拟时，存在较大误差，特别是剪切刚度预测与试验结果存在很大差异。

对于Mullins软化诱导各向异性的研究，国外学者从材料本构关系的角度进行了探索。R. Dargazany等人认为分子网络结构的变化是橡胶材料在发生Mullins软化时出现诱导各向异性的微观机理，并提出模拟橡胶材料Mullins软化各向异性的本构模型[3]。J. Diani等人通过试验验证了Mullins软化诱导各向异性现象，并基于统计热力学理论提出了相应的本构理论来描述这一现象[4]。M. Rebouaha等人基于唯象学理论，提出了计算硅胶材料各向异性软化的本构理论[5]。以上学者所提出的本构理论虽然考虑了Mullins软化的诱导各向异性，能够提高计算精度，但是本构模型非常复杂，本构参数拟合难度很大，难以用于工程实际。本文通过对橡胶纯剪切试样进行多向载荷拉伸试验，研究在剪切载荷作用下橡胶材料的Mullins诱导各向异性，基于伪弹性理论，提出一种Mullins效应软化参数拟合方法，能够方便地应用于工程有限元分析，为提高橡胶弹性元件受剪切载荷的横向刚度预测精度提供设计依据和技术支持。

1 伪弹性理论本构模型

1.1 Mullins软化效应

橡胶材料的Mullins软化效应是指橡胶材料的加载路径与卸载路径不同，在相同位移载荷下，橡胶材料的卸载应力明显低于加载应力。当再次施加小于初始位移水平的载荷时，橡胶材料的应力应变会沿着卸载曲线变化。当施加超过初始位移水平的载荷时，橡胶材料的应力应变会沿着新的加载曲线进行变化。图1为发生Mullins软化效应的加载-卸载应力应变曲线。[6]

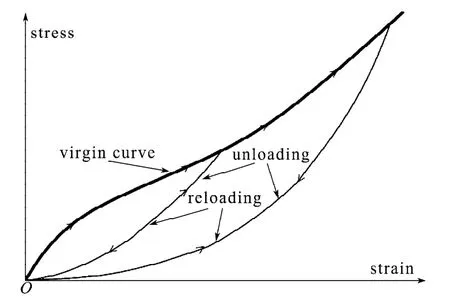
图1 理想的Mullins力学行为Fig.1 The ideal Mullins mechanical behavior

在工程实际中，橡胶弹性元件产品检验都要经过多次的加载卸载循环，以消除Mullins效应，然后再进行刚度检测。而现有的工程有限元分析软件中，经典的橡胶材料超弹本构模型没有考虑Mullins效应，分析的结果往往与试验检测的结果相差很大。为了考虑Mullins效应的影响，提高计算精度，人们发展了伪弹性本构理论[7]。

1.2 伪弹性理论本构参数

基于唯象学的超弹材料本构模型，通过建立应变或拉伸比等加载变量与应变能之间的关系来描述橡胶材料的应力应变行为。为使本构方程能够方便描述Mullins效应，将应变能密度分成畸变应变能密度和体积变化应变能密度2部分[8]，即

式中：U是应变能；Udev是材料初始加载至某一应变下的应变能密度；Uvol是材料体积变化所产生的应变能密度。在超弹模型中增加损伤变量来反映材料的Mullins软化效应，并且将该变量与应变能函数联系起来，伪弹性本构模型可以表示为[8]

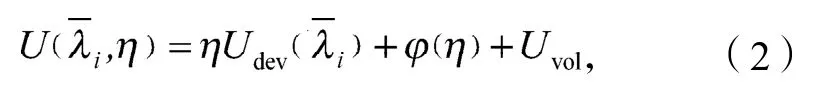
式中：η为损伤变量，其物理意义为橡胶材料在某一变形下，其卸载应力与初始加载应力的比值，如图2所示[8]，图中是加载至相同位移下的应力值，是卸载至相同位移下的应力值；为损伤应变能密度函数；为主拉伸比。

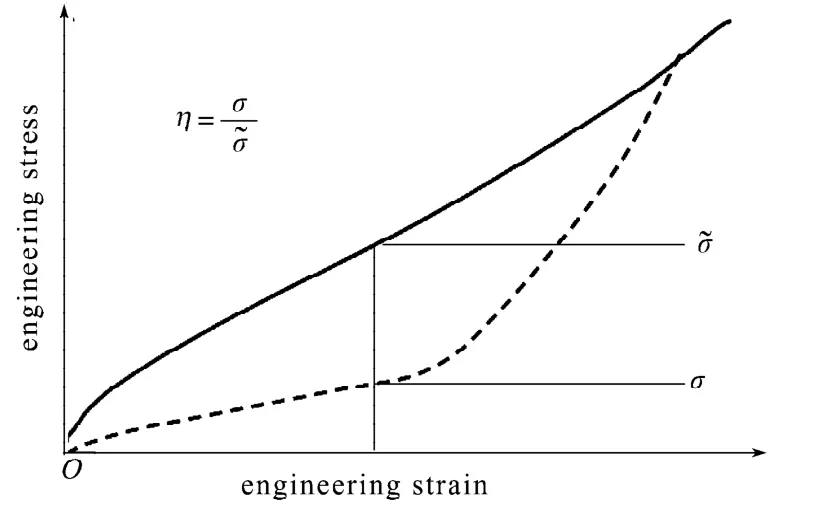
图2 损伤变量的物理意义Fig.2 The physical significance of damage variable

利用应变能计算损伤变量，其解析式为[9]

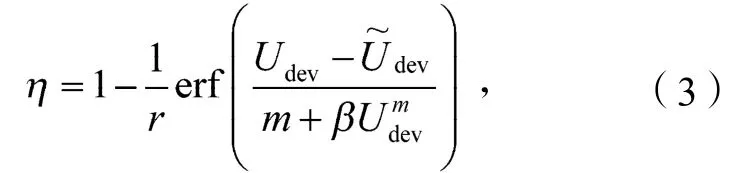
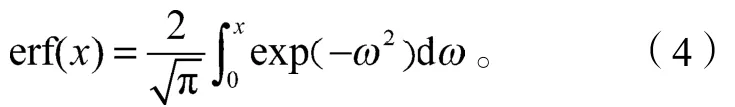
由式（3）可知，3个软化控制参数都与材料软化损伤的大小有着紧密的联系。其中，r值决定了橡胶材料的最大损伤程度，r值越小，橡胶材料所能发生的软化程度就越大；的值与损伤的大小成反比。值越大，软化损伤越小；m为材料软化所需最大应变能的阀值，m值越大；材料发生软化所需的最大应变能的阀值越大，m值的大小对低应变水平加载的软化影响非常大。

伪弹性本构理论没有考虑橡胶的Mullins软化诱导各向异性，将Mullins软化损伤视为是各向同性的。对橡胶弹性元件在单向受载下同向刚度进行仿真时，伪弹性本构理论具有较高的计算精度，但是在预测受多向载荷历程的橡胶产品刚度时，仿真结果与试验值有很大差别。

2 拉/剪载荷下Mullins诱导各向异性试验

2.1 试验原理

大多数橡胶减振元件的使用工况，都是在承担较大轴向载荷的同时还承受横向载荷。某型空气弹簧辅助弹簧如图3所示，该元件在实际使用过程中除承受96.9 kN轴向载荷外，还在顶部有10 mm的横向位移。在这种工况下，橡胶材料同时受到轴向载荷和横向剪切载荷作用。

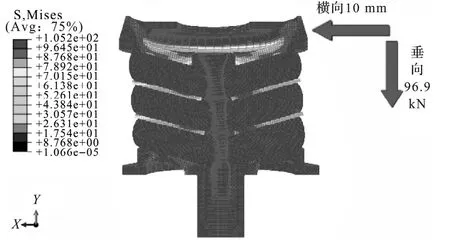
图3 辅助弹簧承载后变形情况Fig.3 The deformation of auxiliary spring under load

课题组设计了2组试验来进行对比，第1组为试验A，第2组为试验B，试验流程如图4所示。

试验A为纯剪切试验，由于试样的宽度远大于其拉伸方向的长度，试样在拉伸过程中宽度方向的拉伸比近似等于1，因而处于纯剪切状态。

试验B是先将试样进行轴向拉伸，然后进行纯剪切试验。橡胶元件通常承受压缩载荷，但是由于橡胶材料的不可压缩性，在受到轴向的压缩载荷时，会在横向发生膨胀，产生很大的拉应力。因此使用轴向拉伸/纯剪切试验（试验B，下文中简称拉/剪试验）可以模拟橡胶弹性元件承受轴向压缩和横向剪切载荷历程的工况，研究橡胶材料在拉/剪载荷下的Mullins诱导各向异性。

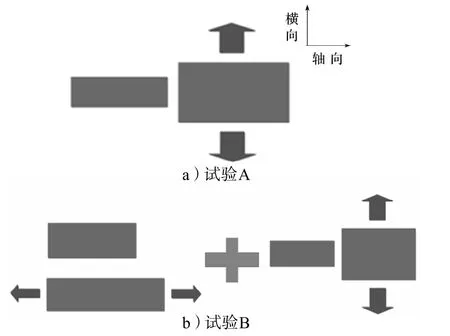
图4 试验示意图Fig.4 Schematic of experiments

2.2 试验方案

试验设备为SANS微机控制万能拉伸试验机，试验温度为24℃，加载速率为5 mm/min。橡胶试样尺寸为60 mm×26 mm×2 mm，剪切试验标距为60 mm× 6 mm×2 mm，试验方案见表1。

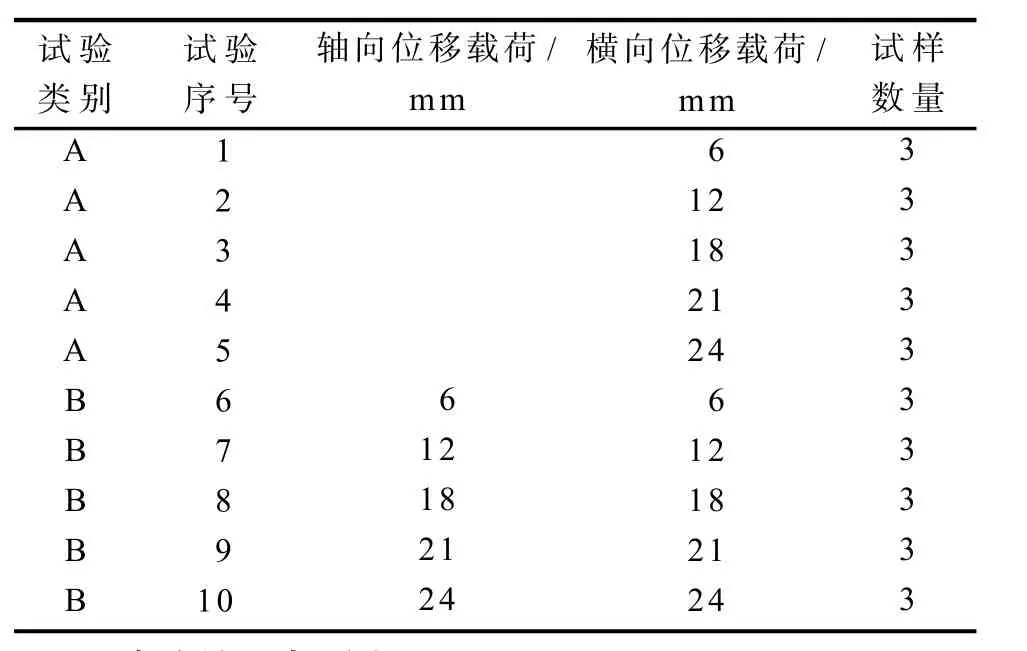
表1 Mullins诱导各向异性试验方案Table 1Experiment scheme of Mullins induced anisotropy

2.3 试验结果与分析

试验结果如图5～7所示。由试验结果可以看出，剪切橡胶试样在经过轴向拉伸以后，横向刚度出现了明显的差异（图中橡胶纯剪切试样的横向刚度计算是用试样在横向所受载荷除以横向位移），而且这种差异会随着轴向拉伸位移载荷水平的增大而增大。由于伪弹性本构理论将Mullins软化损伤看成各向同性的，所以难以准确计算橡胶剪切试样经轴向拉伸变形后的横向刚度。线和试验B刚度曲线的拟合值。

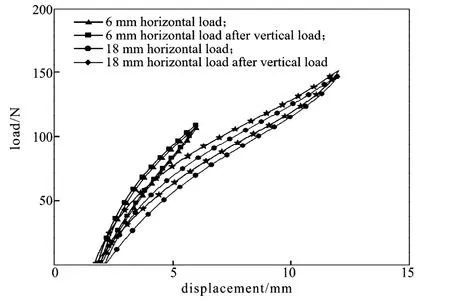
图5 6 和 18 mm 位移载荷下剪切试样横向刚度对比Fig.5 The lateral stiffness contrast under the displacement load of 6 mm and 18 mm

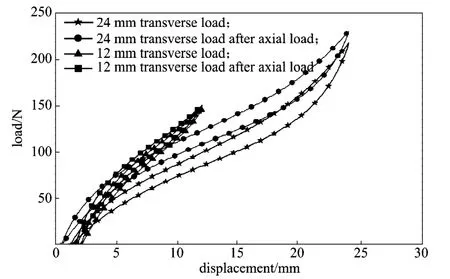
图6 12和 24 mm拉伸位移下剪切试样横向刚度对比Fig.6 The lateral stiffness contrast under the tensiondisplacement of 12 mm and 24 mm

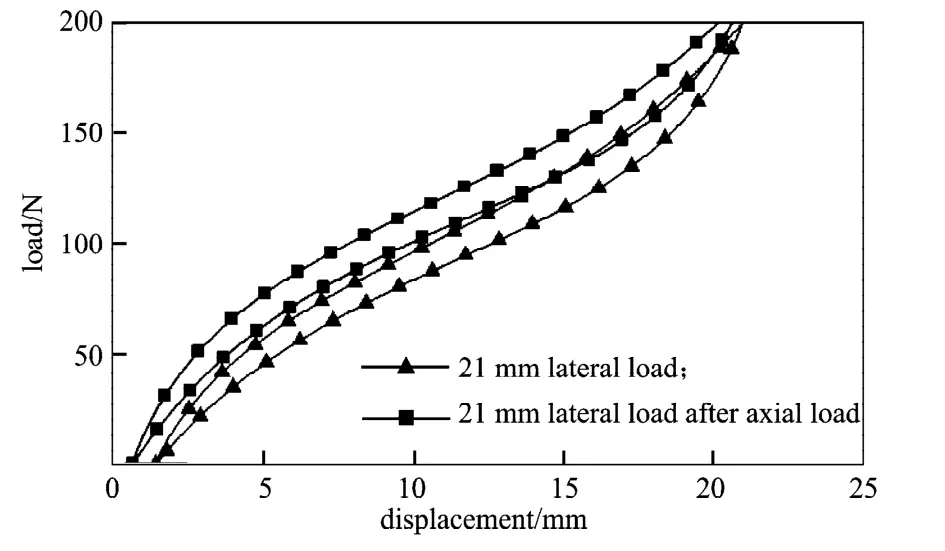
图7 21 mm拉伸位移下各向异性对比Fig.7 Anisotropy contrast under tension displacement of 21 mm

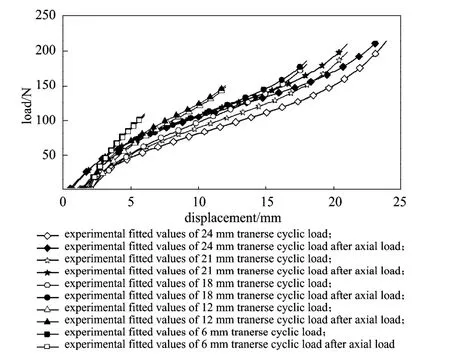
图8 各级位移载荷水平下试验A和试验B软化曲线拟合Fig.8 The soften curves fitting of experiment A and experiment B under different displacement loading levels

为定量描述Mullins软化诱导各向异性的大小随位移载荷水平变化的规律，计算各个位移载荷水平下的试验A刚度曲线和试验B刚度曲线的残差平方和均值，计算式如下[11]，即

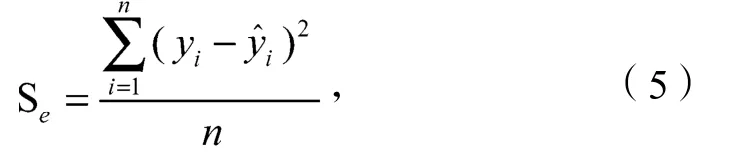
式中：yi为试验A中每个位移载荷水平下载荷；为试验B中每个位移水平下加载至相同位移下的载荷；n为所有的数据点的个数。

表2所示为计算结果，可以看出，随着位移水平的增大，Mullins软化诱导各向异性对于横向刚度的影响越发显著。

表2 残差平方和均值计算结果Table 2The calculated results of mean sum of squared residuals

3 Mullins软化诱导各向异性的数值模拟

3.1 软化控制参数拟合

在Abaqus软件中拟合软化控制参数，首先将最大位移载荷的纯剪切试验数据输入到超弹材料本构模型中，确定试样纯剪切的加载曲线；然后，将每个位移载荷水平纯剪切稳定循环试验数据输入到伪弹性本构模型中。为了分析Mullins软化诱导各向异性的影响，应分别拟合纯剪切试样的剪切软化控制参数与拉/剪软化控制参数。在拟合剪切软化控制参数时，输入试验A每个位移载荷水平的稳定循环数据；而在拟合拉/剪软化控制参数时，输入试验B的每个位移载荷的稳定循环数据。

在Abaqus软件中建立试样的有限元模型如图9所示。

图9 有限元仿真边界条件Fig.9 The boundary conditions for finite element simulation

按照试验情况设置边界条件，并选择Data Check命令，在Abaqus软件中自动生成的DAT文件中输出软化控制参数。利用Abaqus软件拟合得出的软化控制参数见表3。

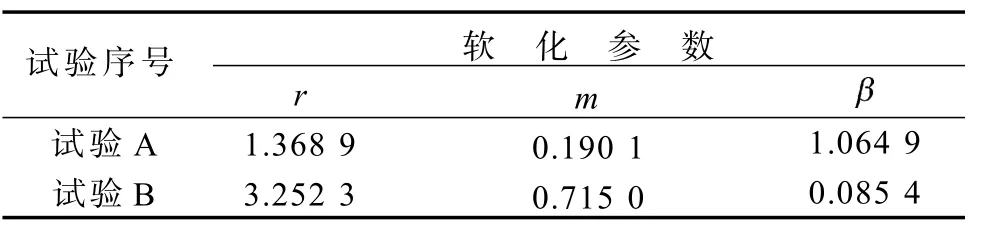
表3 有限元拟合参数Table 3The finite element fitting parameters

3.2 Mullins软化有限元仿真与试验数据对比

由于实际的Mullins软化曲线与理想化的软化曲线存在一些差别，即在循环加载试验中，试样加载曲线与卸载曲线并不会完全重合。为方便仿真结果与试验数据对比，本文利用最小二乘法将试验中的载荷-位移稳定循环加载试验数据拟合成一条五次多项式曲线，用以检验仿真效果。拟合结果为

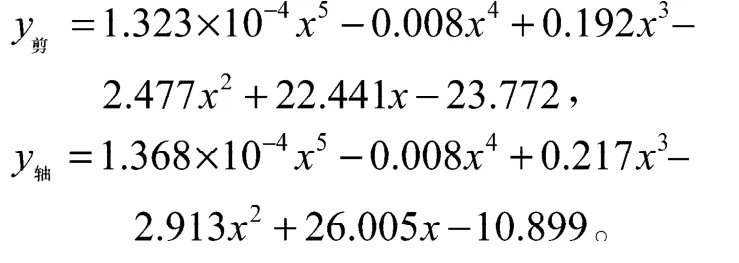
其中：y剪和y轴分别为纯剪切试验和拉/剪试验的载荷值；x为位移。

在24 mm位移载荷水平下，纯剪切和拉/剪试验数据拟合曲线如图10～11所示。纯剪切试验没有考虑Mullins软化诱导各向异性效应，拉/剪试验则考虑了Mullins软化诱导各向异性效应。

从图10～11中可以看出，不考虑Mullins软化效应的有限元分析值与试验结果相差较大，而考虑了软化效应的分析值与试验结果吻合较好。

图12所示为考虑诱导各向异性与不考虑诱导各向异性仿真曲线对比。可以看出，考虑Mullins软化诱导各向异性拟合出的软化控制参数，能够更好的模拟橡胶试样在拉/剪载荷作用下横向Mullins软化效应。残差分析表明，没有考虑诱导各向异性的仿真软化曲线与试验值的残差平方和均值为932.39，而考虑诱导各向异性模拟出的软化曲线与试验值的残差平方和均值为253.47，计算精度显著提高。

图10 24 mm纯剪切试验数据拟合曲线与仿真曲线对比Fig.10 The contrast of fitting curve and simulation curve ofpure shear experiment data of 24 mm

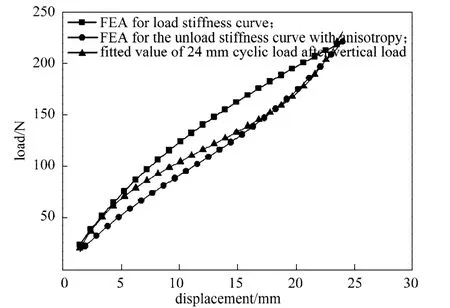
图11 24 mm拉/剪试验数据拟合曲线与仿真曲线对比Fig.11 The contrast of fitting curve and simulation curve of tension/shear experiment data of 24 mm

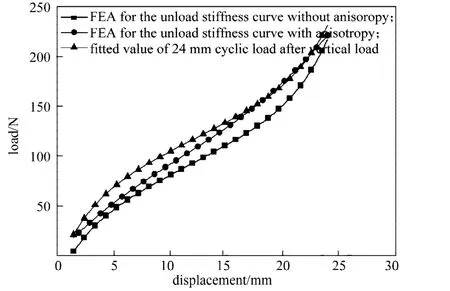
图12 考虑诱导各向异性与不考虑诱导各向异性仿真曲线对比Fig.12 The simulation curves contrast of considering induced anisotropy and without considering induced anisotropy

4 结论

1）使用矩形试样进行5个位移载荷水平的纯剪切和轴向拉伸/纯剪切循环加载试验，结果表明，橡胶材料在发生Mullins软化的同时，还具有Mullins软化诱导各向异性，并且这种软化诱导各向异性会随轴向位移载荷水平的增加而增大。

2）利用橡胶试样的纯剪切和轴向拉伸/纯剪切循环加载试验数据，分别拟合得出橡胶试样在两种载荷历程下的横向Mullins软化控制参数，提出了橡胶材料受拉/剪载荷的横向刚度预测方法。

3）利用拟合软化控制参数对橡胶试样在2种载荷历程下的横向刚度进行有限元仿真，并对仿真估计值与试验值的残差平方和均值进行对比，结果表明，考虑和没有考虑Mullins 软化诱导各向异性的残差平方和均值分别为253.47和932.39，仿真精度明显得到提高。

[1]方建辉，丁智平，卜继玲，等. 橡胶减振支座动态性能仿真分析研究[J]. 湖南工业大学学报，2014，28(2)：16-22. Fang Jianhui，Ding Zhiping，Bu Jiling. Simulation Research on Dynamic Performance of Rubber Damping Brackets of Wind Turbine[J]. Journal of Hunan University of Technology，2014，28(2)：16-22.

[2]Diani J，Fayolle B，Gilormini P. A Review on the Mullins Effect[J]. European Polymer Journal，2009，45(3)：601-612.

[3]Dargazany R，Itskov M. A Network Evolution Model for the Anisotropic Mullins Effect in Carbon Black Filled Rubbers[J]. International Journal of Solids and Structures，2009，46(16)：2967-2977.

[4]Diani J，Brieu M，Vacherand J M. A Damage Directional Constitutive Model for Mullins Effect with Permanent Set and Induced Anisotropy[J]. European Journal of Mechanics，2006，25(3)：483-496.

[5]Rebouah M，Machad G，Chagnon G，et al. Anisotropic Mullins Stress Softening of a Deformed Silicone Holey Plate [J]. Mechanics Research Communications，2013，49：36-43.

[6]Cantournet S， Desmorat R， Besson J. Mullins Effect and Cyclic Stress Softening of Filled Elastomers by Internal Sliding and Friction Thermodynamics Model[J]. International Journal of Solids and Structures，2009，46(11/12)：2255-2264.

[7]Ogden R W，Roxburgh D G. A Pseudo-Elastic Model for the Mullins Effect in Filled Rubber[J].Proceedings of the Royal Society，1999，455：2861-2877.

[8]张友南，黄友剑. 多轴承载下基于Mullins效应的非线性刚度的分析方法[J]. 计算机辅助工程，2013，22(增刊2)：360-363. Zhang Younan，Huang Youjian. Analysis Method for Non-Linear Stiffness Under Multi-Axis Loading Condition Basedon Mullins Effect[J]. Computer Aided Engineering，2013，22(S2)：360-363.

[9]Ryan E P，Will V M. Implications of the Mullins Effect on the Stiffness of a Pre-Loaded Rubber Component ABAQUS Users’ Conference[EB/OL]. 2014-07-15. http：//www. axelproducts.com/downloads/PaigeMars.Pdf.

[10]Hoffman J D. Numerical Methods for Engineers and Scientists [M]. New York：McGraw Hill Inc，1992：378.

[11]王岩，隋思涟，王爱青. 数理统计与MATLAB工程数据分析[M]. 北京：清华大学出版社，2006：165. Wang Yan，Sui Silian，Wang Aiqing. Mathematical Statistics and MATLAB Engineering Data Analysis[M]. Beijing：Tsinghua University Press，2006：165.

（责任编辑：申剑）

Study on Mullins Softening Induced Anisotropy of Rubber Materials Under Tension/Shear Loads

Li Fei1,2，Ding Zhiping1，Bu Jiling2，Huang Youjian2
（1. School of Mechanical Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China；2. Zhuzhou Time New Material Technology Co.,Ltd.,Zhuzhou Hunan 412007,China）

Conducts pure shear and axial tension/ pure shear experiments on rectangular rubber specimens under different displacement load levels,and investigates Mullins softening induced anisotropy of rubber materials under tension/ shear load. The experimental results show that because of the effect of Mullins softening induced anisotropy,the pure shear test on the specimens after axially tensions causes the specimen lateral stiffness increasing. Uses the axial tension/ pure shear experiment data of rubber specimens to fit and obtain the relevant Mullins softening control parameters,and reflects the effect of Mullins softening induced anisotropy on the transverse stiffness. Makes finite element simulation on he transverse stiffness curves of the specimens under two kinds of load tests,and compares the mean sum of squared residuals between the simulation estimate value and the experimental value. It is considered that Mullins softening induced anisotropy will significantly increase the prediction accuracy of transverse shear stiffness of rubber elements under tension and shear load.

rubber；pure shear；Mullins softening；induced anisotropy；finite element；stiffness

Q334.9

A

1673-9833(2015)01-0038-06

2014-11-02

中央财政创新团队专项基金资助项目（0420036017），湖南省十二五机械工程重点学科基金资助项目（湘教发[2011]-76号）

李飞（1986-），男，辽宁丹东人，湖南工业大学硕士生，主要研究方向为机械结构强度理论及应用，

E-mail：woshitiancailifei@163.com

丁智平（1956-），男，湖南桃江人，湖南工业大学教授，博士，主要研究方向为机械结构强度理论及应用，E-mail：472447034@qq.com

10.3969/j.issn.1673-9833.2015.01.007