核磁共振技术检测钚复合构件

苟振志，何彬，赵尚文，钟依禄，李俊，喻凤梅

（1.第二炮兵工程大学，陕西西安710025；2.96421部队，陕西宝鸡721012；3.第二炮兵装备研究院，北京100085）

核磁共振技术检测钚复合构件

苟振志1，2，何彬1，赵尚文2，钟依禄2，李俊3，喻凤梅1

（1.第二炮兵工程大学，陕西西安710025；2.96421部队，陕西宝鸡721012；3.第二炮兵装备研究院，北京100085）

该文仿真计算在不同外磁感应强度下，钢铍钚复合构件各球壳静磁场分布及缺陷样品磁场分布情况。结果表明：不同的磁场强度和磁导率对复杂金属结构的磁场分布不一样，总的来说，磁感应强度越大，磁导率越小，则各球壳层磁场强度越大。外磁场能够深入钚复合构件多层结构且保持一定强度和均匀性，满足声-核磁共振无损检测系统的要求。最后对无缺陷和有缺陷的样品进行磁场分布模拟，对比结果表明：钚复合构件中气泡、裂纹等缺陷可通过探测磁场分布进行定性判断，为下一步声核磁共振检测技术奠定理论基础。

核磁共振；钚复合构件；磁通测量；仿真计算

本文提出核磁共振[5-8]、超声和超导量子干涉器件（superconducting quantum interference device， SQUID）相结合，通过超声和核自旋的耦合作用建立一种基于声-核磁共振的钚复合构件无损检测新方法。

这种方法的总体思想是：首先将钚复合构件置于高强度外磁场中，因塞曼效应[9-10]引起磁性核的自旋能级分裂，再用满足一定条件的超声能量激发自旋核能级共振跃迁，最后利用SQUID对磁通的高度敏感性测定该超声-核磁共振信号。

本文拟通过数值仿真研究钚复合构件的核磁共振特性，为钚构件的声核磁共振研究提供理论基础。

1 钚复合构件模型参数

1）各壳层厚度：设各层为均匀球体，最外层不锈钢层厚度为3mm，中间铍层厚度3mm，最内层钚层3mm。

2）各壳层半径：Φ130-133-136-139mm。

3）表面光洁度：设为理想情况。

4）粘接情况：考虑完全密结，未考虑粘接情况及粘接剂性质。

5）各层简称：为了表述方便，称不锈钢层为3#材料，铍层为2#材料，钚层为1#材料。

6）电磁参数及声学参数：分别如表1、表2所示。

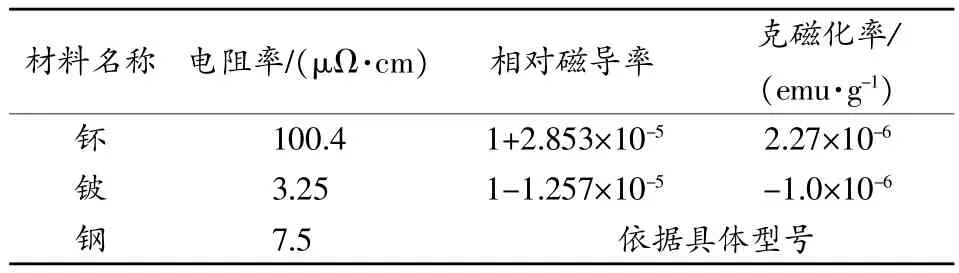
表1 电磁参数

表2 声学参数

传播速度由模型的实际情况选用理论公式计算得出。

纵波在固体中的声速：

薄板中：

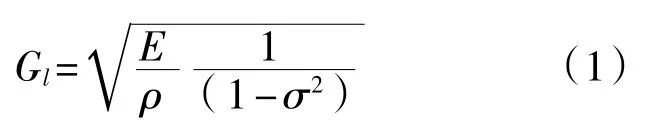
无限介质中：

横波在固体中的声速：

无限介质中：

式中：Gl——声速；

E——杨氏模量；

ρ——密度；

G——剪切模量；

σ——泊松比；

K——体积模量。

2 钚复合构件壳层中静磁场的分布

2.1 计算模型的建立

计算模型如图1所示。

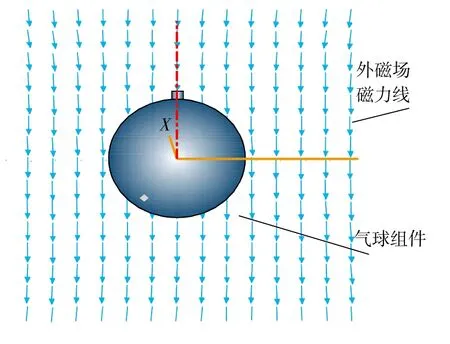
图1 钚复合构件计算模型

2.2 不锈钢磁导率及静磁场磁感应强度对钚复合构件磁强分布的影响

数值计算过程中的最外层不锈钢壳层并不严格限于单一性质参数，而是在可能的范围给出了一系列值进行计算，这能够为声-核磁共振军控核查属性测量提供参考；静磁场的磁感应强度取值范围为1～15T，数值计算中的磁感应强度在磁共振波谱研究的实验室强度范围内。

2.2.1 不锈钢球壳为低磁导率奥氏体不锈钢

算例1：外磁场的磁感应强度为1T时，1#（μr=1+ 2.853-5），2#（μr=1-1.257-5），3#（奥氏体μr=1.8），各层完全密接条件。

从图2（a）可以看出，磁感应强度为1T时，不锈钢层球壳在赤道周围磁场强度最大，磁场强度分布以赤道对称。

从图2（b）可以看出，磁感应强度为1T时，铍层除了极点附近磁场强度稍弱外，磁场强度分布非常均匀。

从图2（c）可以看出，磁感应强度为1T时，钚层除了极点附近磁场强度稍弱外，磁场强度分布非常均匀。

可见在不锈钢壳层为低磁导率的情形下，钚复合构件最内层钚材料和中间层铍材料的磁场分布基本一致，磁场分布主要受不锈钢层影响。

算例2：外磁场的磁感应强度为10T时，1#（μr=1+ 2.853-5），2#（μr=1-1.257-5），3#（奥氏体μr=1.8），各层完全密接条件。

从图3（a）可以看出，磁场强度以赤道面呈对称状分布，说明增加磁场强度，外层金属壳体磁场分布仍然呈现明显的规律分布特征。

从图3（b）可以看出，磁感应强度为10T时，磁场分布较图2（b）来说不太均匀，说明单纯增加磁感应强度，铍层磁场强度分布会呈现分布不均的现象。

从图3（c）可以看出，磁感应强度为10T时，钚层外壳磁场强度分布和铍层基本相同。比较图2（c）和图3（c）可以得出，单纯增加磁感应强度，最内层的钚层磁场强度分布也会呈现分布不规则的特点。

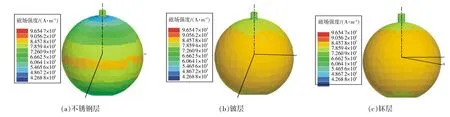
图2 磁感应强度为1T，不锈钢μr=1.8时不锈钢层、铍层、钚层磁场强度分布

图3 磁感应强度为10T，不锈钢μr=1.8时不锈钢层、铍层、钚层磁场强度分布

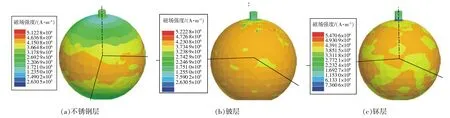
图4 磁感应强度为15T，不锈钢μr=100时不锈钢层、铍层、钚层磁场强度分布

图5 磁感应强度为15T，不锈钢μr=2000时不锈钢层、铍层、钚层磁场强度分布

2.2.2 不锈钢球壳为高磁导率不锈钢

在军控核查和防扩散中需探测对密封在高磁导率容器中的敏感材料，这里用两种能产生磁屏蔽的高磁导率外壳为例，计算其磁场分布。

算例1：外磁场的磁感应强度为15T时，1#（μr= 1+2.853-5），2#（μr=1-1.257-5），3#不锈钢（μr=100），各层完全密接条件。

从图4（a）可以看出，当磁感应强度为15 T，3#μr=100时，磁场强度分布较图1（a）和图2（a）分散，说明增加磁导率，不锈钢层的磁场强度分布会变得不规则。

从图4（b）可以看出，当磁感应强度为15T，整个铍层磁场强度分布较均匀，磁场强度也较图1（b）和图2（b）强。

从图4（c）可以看出，当磁感应强度为15T，钚层较图1（c）和图2（c）分布呈现明显的不规则性，说明增加磁感应强度和改变外层磁导率会影响内层金属的磁场强度分布。

算例2：外磁场的磁感应强度为15T时，1#（μr= 1+2.853-5），2#（μr=1-1.257-5），3#不锈钢磁导率非常大（μr=2000），各层完全密接条件。

从图5（a）可以看出，在磁感应强度高磁导率条件下，不锈钢外壳层赤道附近的磁场强度和两极附近的磁场强度有1个数量级的差别，磁场分布较图4（a）没有大的改变，故单纯增加外层不锈钢的磁导率对外层壳体影响不明显。

从图5（b）可以看出，在外层壳体处于高磁导率时，铍层赤道附近和两极附近磁场强度处于同一量级，且分布比较均匀，磁场强度明显降低。

从图5（c）可以看出，在外层高磁导条件下，最里层的钚层还是获得了比较均匀的磁场强度。同时比较图4（c）可以看出，高磁导率情况下最里层的金属磁场强度降低。

3 缺陷样品的磁场仿真特性研究

考虑钚复合构件结构的复杂性，仿真时对模型进行简化处理，建立如图6所示的模型。图中代表外加静磁场环境，它主要是由100mm×100mm×100mm的正方体产生的均匀磁场，仿真时所取磁场方向为沿y轴的正方向，磁感应强度为1.000 05T；图中a、b分别表示样品及缺陷的具体形状和相对位置，样品及缺陷的中心坐标为（50mm，50mm，50mm），样品形状假定为40mm×40mm×40mm的正方体，其材料组成为铝，缺陷位于样品中心，也假定为一个10mm×10mm×10mm的正方体，其内部为空气，即仿真计算时假定缺陷是具有一定大小的气泡。

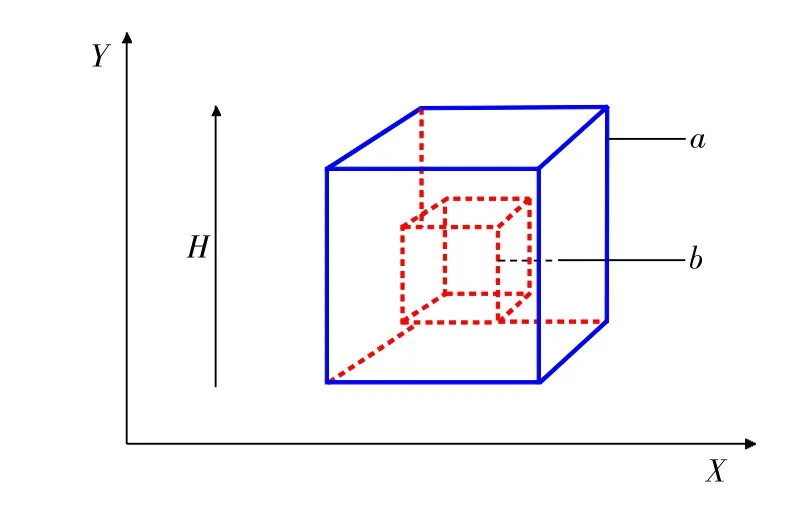
图6 缺陷仿真模型示意图

仿真过程中，根据模型及计算简化等方面的考虑，仅在模型中选取沿磁场方向高度为50mm平面中的一条路径进行仿真，并在该平面的若干仿真路径中选择如表3和表4所示的11个位置处的磁场强度值进行计算，该11个点仅代表样品中部分位置的磁场分布情况。事实上在仿真中选取不同位置点就可以得到更为详细的仿真结果，但是由于文中仅对该方法进行定性说明，就没有选取所有点进行计算，仅选择了部分位置进行计算。仿真计算结果如表3和表4所示，其中表3是样品中没有缺陷存在磁场强度值，表4是存在缺陷时对应点的磁场强度值。

表3 样品无缺陷时磁场强度值

表4 样品有缺陷时磁场强度值

图7 样品有无缺陷时磁感应强度对比图

根据磁场基本理论可知，一些材料由于存在缺陷会在其内部产生残余磁场，并且缺陷尺寸越大，产生的残余磁场越大。对表3和表4中的数据进行分析可以得出如图7所示的结果。

从图中可以看出，存在缺陷时材料内部的磁场分布发生了变化，从曲线变化的趋势可以大致判断缺陷位于45～55mm之间，事实上本文仿真时缺陷的位置正是设置在该处，这说明利用该种方法对材料内部缺陷进行定性判断是可行的。

4 结束语

外磁场的大小对于各层球壳上磁场强度分布有很大影响，起主导作用。外磁场强度越大则各球壳层上的感应磁场也越大，且内层球壳的磁场分布更均匀；最外层不锈钢球壳的磁导率对内层球体磁场分布影响较大，其相对磁导率越大则各球壳层上的磁场越小，但相应增加外磁场强度后内层球体磁场强度也大幅增加；在同一计算模型及条件下，内层球面上的磁场大小和外层球面上的磁场大小差异不大。总的趋势是内层球面的磁场小于外层球面上的磁场；在不同的场强和不锈钢磁导率条件下，铍层和钚层磁场分布基本相同，即铍层对钚复合构件内层的场强分布影响不大；外磁场能够深入钚复合构件的多层结构，且保持相当的强度，满足声-核磁共振检测系统要求。

[1]苟振志，何彬，喻凤梅，等.铅组件模拟钚组件氧化腐蚀性研究[J].无损检测，2014，36（1）：5-10.

[2]钚冶金[M].北京：中国科学院原子核科学委员会编辑委员会，1967：57-69.

[3]强亦忠.常用核辐射数据手册[M].北京：原子能出版社，1990：113-125.

[4]杜祥琬.核军备控制的科学技术基础[M].北京：国防工业出版社，1996：72-79.

[5]李彬.军备控制理论与分析[M].北京：国防工业出版社，2006：60-89.

[6]Proctor W G，Tantilla W H.Influence of ultrasonic energy on the relaxation of chlorine nuclei in sodium chlorate[J].Phys Rev，1956（101）：1757-1763.

[7]Bolef D I，Menes M.Nuclear magnetic resonance acoustic absorption in KI and KBr[J].Phys Rev，1959（114）：1441-1451.

[8]Menes D I.Bolef observation of nuclear resonance acoustic absorption of In115 in InSb[J].Phys Rev，1958（109）：218-219.

[9]Bolef D I.Acoustic techniques in magnetic resonance[J]. Science，1962（136）：359-369.

[10]Gregory E H，Bommel H E.Acoustic excitation of nuclear spin resonance in single crystalline tantalum[J]. Phys Rev Lett，1965（15）：404-406.

Nuclear magnetic resonance technique for detection of plutonium component

GOU Zhenzhi1，2，HE Bin1，ZHAO Shangwen2，ZHONG Yilu2，LI Jun3，YU Fengmei1
（1.Second Artillery Engineering University，Xi’an 710025，China；2.Troops No.96421，Baoji 721012，China；3.The Second Artillery Equipment Research Institute，Beijing 100085，China）

In this paper，the simulation calculation is used to test the magnetic field fall under the shell layers of the steel-beryllium-plutonium composite balloon subassembly and the distribution of the magnetic field in the objection sample in different magnetic strength fields.The result shows that the magnetic field strength and permeability are different for complex metal structure of the magnetic field-distribution.In general，the larger the magnetic induction intensity is，the smaller the ball shell permeability，the greater the magnetic field strength.the best measure effect in the experiment was obtained when the magnetic field strength of 10T was operated.The results of comparing the simulation results of magnetic field distribution of defects in the sample with the experiment results shows that the researching cracks and other defects is feasible through the magnetic field component in the bubbles.

nuclear magnetic resonance；plutonium components；flux measure；simulation calculation

A文章编号：1674-5124（2015）08-0113-05

10.11857/j.issn.1674-5124.2015.08.026

0 引言

在多种因素的复合作用下，钚复合构件[1]会出现不同材料层的脱粘与渗透、内部钚材料氧化等现象。钚复合构件的密封结构、材料特性及细微变化都会给常规检测造成困难[2]，如传统的射频电磁波无法穿透钚复合构件的多层结构到达内层[3-4]。

2014-10-11；

2014-11-28

国家自然科学基金（51271198，A040103）

苟振志（1978-），男，四川通江县人，工程师，博士，主要从事无损探伤及状态监测研究。