直线拟合的高准确度投影结构光系统标定算法研究

董建民，李东晶

（山东工业职业学院，山东淄博256414）

直线拟合的高准确度投影结构光系统标定算法研究

董建民，李东晶

（山东工业职业学院，山东淄博256414）

针对现有投影仪-相机结构光测量系统标定算法准确度不高的问题，提出一种基于直线拟合的高准确度标定算法。该算法首先找到系统灰度响应线性度较好的灰度区间，在该区间内采用三频四步相移算法对相机获取的投影光栅图像进行相位恢复。然后计算出棋盘格角点在相机坐标系中的坐标，并找到这些角点在投影仪图像中的对应像素点，通过直线拟合的方法进行优化，提高匹配点的搜索准确度。最后采用双目视觉的标定方法实现投影结构光系统的标定。系统标定实验的结果验证所提出的基于直线拟合的标定算法具有较高的标定准确度，有助于后续高准确度的三维重建与测量。

三维测量；校准；相位计算；直线拟合

如何对投影仪和相机组成的光学系统进行标定，是实现高准确度的三维测量需要解决的首要问题[7-8]。目前最受欢迎的标定方法是将投影仪等效成一个逆向的相机，进而通过成熟的双目视觉系统标定技术来标定该投影结构光系统。这种方法首先通过投影仪向棋盘格标定板上投射出一系列正弦变化的相移图像，并用相机进行捕获；然后对相移图像进行解相位；最后从相机得到的图像中提取出棋盘格角点，并找到投影仪图像中的对应点，从而进行系统标定。然而，由于棋盘格标定板中不同颜色的格子对光栅图案的灰度响应是不一样的，现有的投影仪结构光标定算法在标定板区域解相位的准确度并不高，因此难以得到高准确度的标定结果，进而限制了整个三维测量系统的准确度。本文针对这一问题进行深入研究，给出一种基于直线拟合的高准确度的标定算法，从而为后续的高准确度三维重建与测量提供保障。

1 基于三频外差的相位计算

为实现投影仪和相机的联合标定，需要使投影仪具有“拍摄”棋盘格标定板的能力，这就要对投影仪的光栅图像进行准确的解相位。本节将从相位移算法和相位展开两部分介绍如何进行相位计算。

1.1 四步相移算法

相移法的基本原理是采用投影仪向场景中投影出具有一定相位差的正弦光栅图像，当这些结构光照射到物体上时，会受到物体表面的调制而发生形变，通过相机采集这些变形的光栅图像，便可以恢复出每一个像素点处的相位值。本文采用的是标准的四步相移算法，该方法对系统的偶次谐波及随机噪声具有很好的抑制作用。

假设投影仪投射出的光栅图像光强分布为

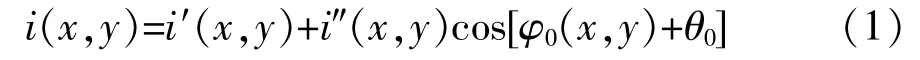
式中：i′（x，y）——期望的灰度均值；

i″（x，y）——期望的灰度变化幅值；

θ0——图像的初始相位值；

φ0（x，y）——像素点（x，y）处的相位值。

在实际测量过程中，由于环境光不可能被完全去除，且投影仪和相机都存在一定的非线性特性，因此系统的灰度响应也是非线性的，需要找到一个线性度较好的灰度区间作为投影灰度的范围。用投影仪向一个白色平板上依次投影灰度值为0～255的灰度图像，然后计算相机所采集图像的灰度均值。通过实际测量发现，本文使用的系统在[120，200]的灰度区间内线性度最好，如图1所示。因此，将i′（x，y）设定为160，将i″（x，y）取为40。那么，可以得到相移为π/2的4幅正弦光栅图像：

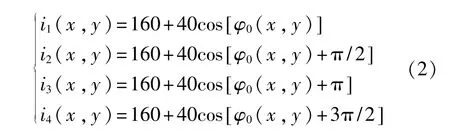
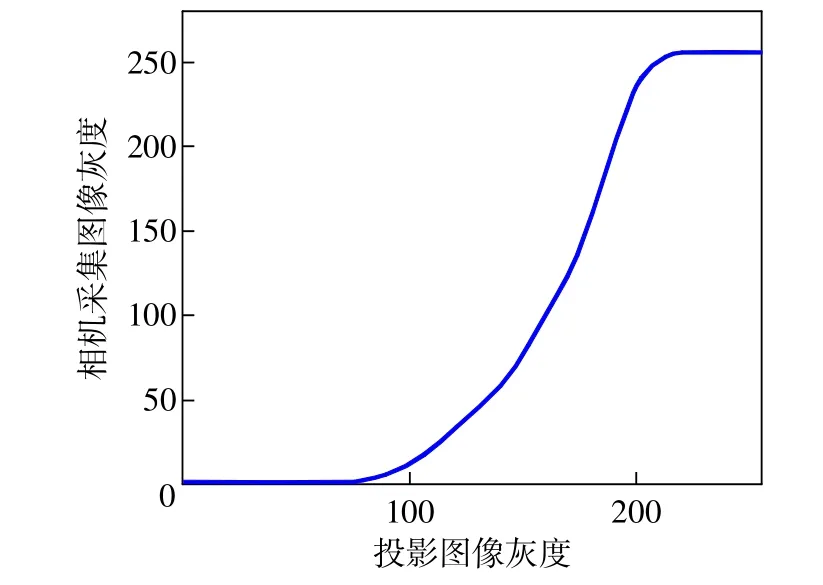
图1 灰度响应测试曲线

相位值φ0（x，y）的计算需分为投影竖条纹和横条纹两种情况：

式中：T——条纹的周期数；

w、h——投影图像的宽和高。

将上述4幅光栅图像分别投影到场景中，并用相机对其进行捕获。相机采集到的图像灰度也应具有式（2）的形式，如下所示：

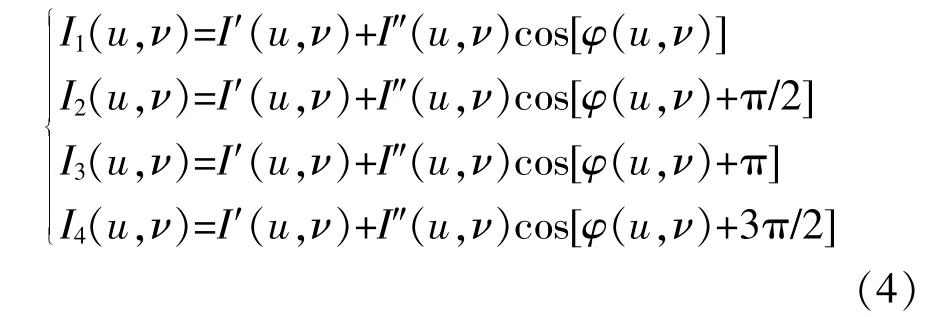
式中：I′（u，ν）——叠加了环境光后的图像灰度均值；

I″（u，ν）——拍摄到图像的灰度变化幅值；

φ（u，ν）——相机坐标系中像素点（u，ν）处的相位值。

对式（4）进行简单的推导便可以得到相位值φ（u，ν）的计算公式为

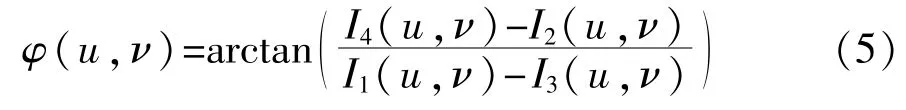
由式（5）得到的相位结果位于[0，2π]区间，即被2π包裹着的。为得到单个周期的连续相位值，需要对其进行相位展开。

1.2 基于三频外差的相位展开

现有的相位展开算法可以分为两类：基于空间的相位展开算法和基于时间的相位展开算法。基于空间的方法仅需要投影一幅图像，效率较高，但分辨率较低；基于时间的方法可以得到更高的分辨率和精度，且对物体表面的形状没有任何要求。

本文采用基于时间编码方法中的三频外差编码策略[9-10]。该方法先后向场景中投影频率为f1=1/ 70、f2=1/64、f3=1/59的相移图像各4幅，即一共12幅图像。假设根据这3种频率的四步相移图像由式（5）求出的相位图像分别为φ1（u，ν）、φ2（u，ν）、φ3（u，ν）。由φ1（u，ν）和φ2（u，ν）这两幅相位图像，可以计算得到一幅新的相位图，其相位值为

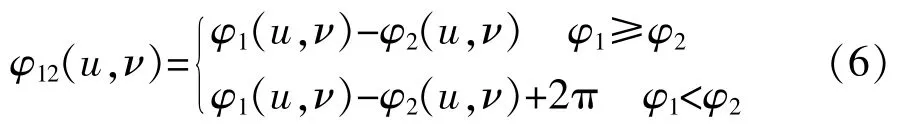
该相位图像对应的频率为

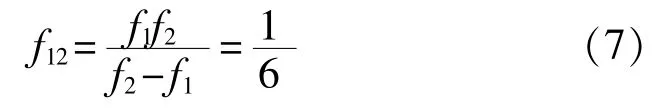
类似地，可以由φ2（u，ν）和φ3（u，ν）得到新的相位图像φ23（u，ν），其频率为f23=1/5。进一步地，再通过这两幅新的相位图像，可以得到相位图像φ123（u，ν），其频率为f123=1。该相位图的频率为1，意味着在整个图像中仅存在一个相位周期，因而能够将不同的像素点区分开来。然而，该图像中的相位值变化范围为[0，2π]，还需要将其恢复成式（3）所给出的变化范围。

这里可以由3种频率中的任意一种频率进行恢复，本文采用第一种频率进行恢复。令

其中round（）为取整函数，T1=1/f1=70。则最终恢复出的绝对相位值可由下式求得：

2 投影结构光系统标定

高准确度的标定结果对投影结构光系统的测量准确度起着至关重要的作用，本节提出一种基于直线拟合的标定算法，可以取得较高的标定准确度。

图2 标定用的红蓝棋盘格标定板

2.1 标定方案

目前广泛使用的投影结构光系统标定算法是将投影仪等效成一个逆向的相机，然后用成熟的双目视觉标定技术来进行标定。传统的双目视觉标定方法是用相机从不同角度拍摄一个黑白交错的棋盘格标定板，然而由于投影仪投射出的是黑白相间的正弦光栅，这些光栅条纹在黑色棋盘格中很难被分辨出来，因此无法用黑白颜色的棋盘格进行标定。本文采用如图2所示的红蓝棋盘格标定板进行系统的标定，该标定板对黑白条纹的影响很小，而且通过投影仪投射红色光便可以用相机拍摄到类似黑白棋盘格的图像。标定过程中拍摄的图像如图3所示。

具体的标定方案如下：

1）调整棋盘格标定板的姿态；

2）投影仪投射红光，用相机拍摄标定板图像；

3）投影仪投射3个频率的四步相移竖条纹图像（共12幅），并用相机拍摄相应的图像；

4）投影仪投射3个频率的四步相移横条纹图像（共12幅），并用相机拍摄相应的图像；

5）重复上述步骤10～15次。

图3 标定过程中拍摄的图像

2.2 系统的内外参数标定

2.2.1 摄像机标定

通常情况下，相机的成像模型都用小孔成像模型来表示。对于世界坐标系中的任意一点P（X，Y，Z），对应于相机图像坐标系中的一个像素点（u，ν），则有如下关系成立：

式中：s——尺度因子；

A——相机的内参数矩阵；

T——相机的外参数矩阵。

目前有很多成熟的摄像机标定技术，如Bouguet方法等。本文采用Matlab提供的detect Checker board Points函数提取出棋盘格图像的角点坐标，然后用estimate Camera Parameters函数进行标定，从而得到相机的内参数矩阵。

2.2.2 投影仪标定

为了对投影仪进行标定，需要使投影仪具有捕获棋盘格角点的能力，这就需要将摄像机捕获的角点与投影仪图像关联起来，进而求出棋盘格角点在投影仪图像中的坐标。

假设在拍摄标定图像的过程中对于棋盘格标定板的某个姿态，从红光下拍摄的图像中提取的某个角点在相机图像坐标系下的坐标为（xc，yc），从竖条纹及横条纹图像中恢复的相位图分别为Φν（u，ν）和Φh（u，ν）。首先需要找到角点（xc，yc）处的相位值。为了减小观测噪声对标定结果的影响，用角点邻域Ω中相位的均值作为该角点处的相位值，如下式所示：

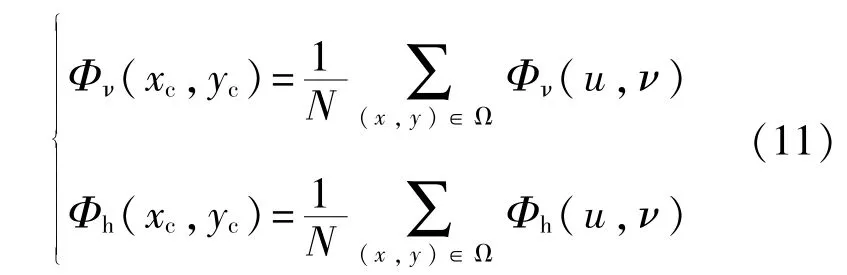
式中N为邻域Ω中像素的个数。接下来便可以求出投影仪图像坐标系中对应于这两个相位值的像素点坐标（up，νp）：

对摄像机捕获的所有棋盘格角点进行上述的运算，可以得到所有棋盘格角点在投影仪图像中的坐标。然而，由于红色格子和蓝色格子对黑白条纹的灰度响应不一致，在标定板区域恢复出的相位值存在一定的误差，由此计算出的棋盘格角点在投影仪图像中的坐标也是不准确的，如图4所示。

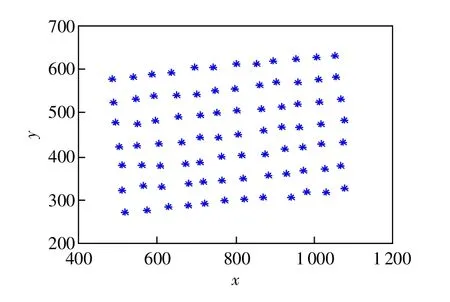
图4 直接计算得到的棋盘格角点坐标

图5 直线拟合后得到的角点坐标

为提高投影仪捕获棋盘格角点的准确度，将上述角点坐标进行直线拟合，得到7条竖线和12条横线。然后计算这些直线的交点，用这些交点的坐标来表示棋盘格角点的坐标，最终结果如图5所示。通过与图4对比可以发现，得到的角点坐标更加接近真实值。

得到准确的棋盘格角点坐标后，仍然使用Matlab中的estimate Camera Parameters函数对投影仪进行标定，从而得到投影仪的内参数矩阵。

2.2.3 系统的联合标定

得到棋盘格角点在相机图像坐标系及投影仪图像坐标系中的坐标后，直接使用Matlab中的estimate Camera Parameters函数就可以很方便的得到系统的所有参数。

3 实验与分析

3.1 系统标定实验

按照上节给出的标定方案，进行了整个系统的标定实验，比较了现有方法和本文所提出方法的标定准确度。在实际的实验中，棋盘格的尺寸为31.65mm× 31.65mm；共采集了12组有效的实验数据，即对应棋盘格12个姿态。下面将从投影仪标定和系统联合标定分别给出对比结果。

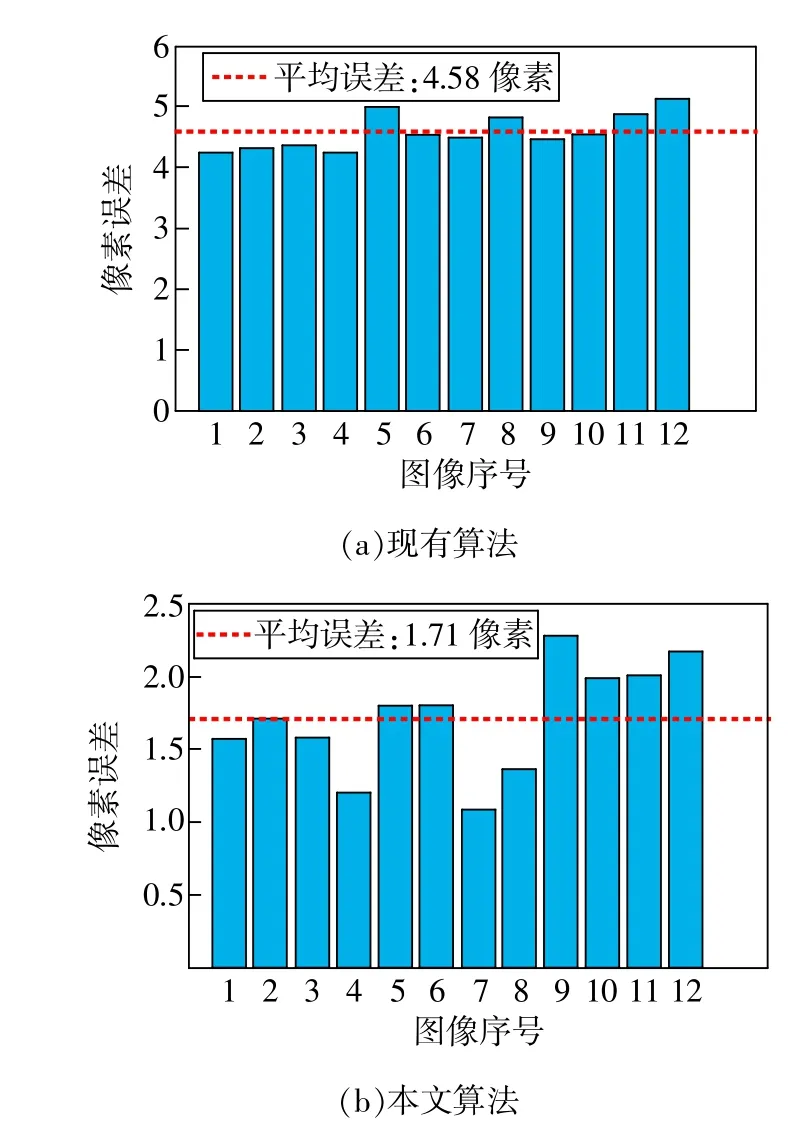
图6 投影仪标定误差统计

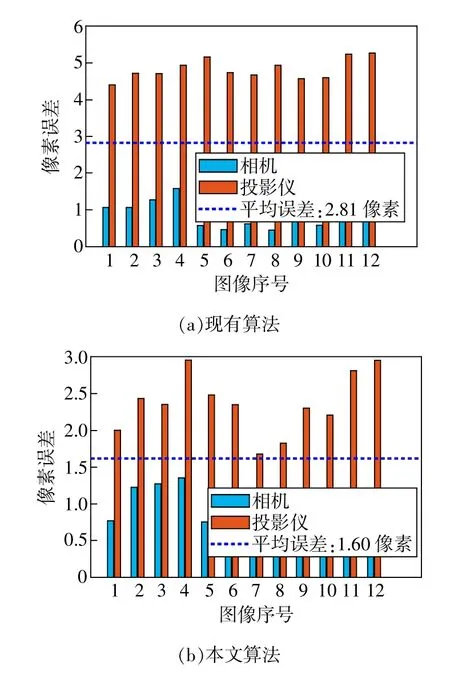
图7 系统联合标定误差统计

图6（a）为现有方法得到的投影仪标定误差统计，平均误差为4.58个像素。图6（b）为本文算法得到的投影仪标定误差统计，平均误差仅为1.71个像素，准确度得到了显著的提升。

图7（a）为现有方法得到的系统联合标定误差统计，摄像机与投影仪的平均误差为2.81个像素。图7（b）为本文算法得到的误差统计，平均误差为1.60个像素，可见整个系统的标定准确度也得到了较大程度的提高。

3.2 平面重建实验

为进一步验证本文所提算法的有效性，对一个标准的平板进行了三维重建实验，投影仪到被测平板的距离为1m左右。重建结果如图8所示，上下两张图分别为两个不同视角下的观测结果。从结果图中可以看出重建的平面平整度非常高，通过计算得到拟合平面的误差为1.27mm，充分验证了本文所提出算法的有效性。

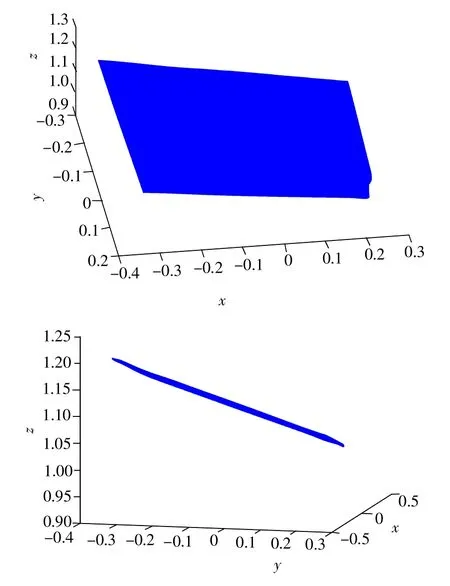
图8 不同视角下的平板三维重建结果

4 结束语

研究了投影仪-相机结构光系统的灰度相应特性，得到了线性度较好的灰度区间。在该灰度区间内，采用三频四步相移算法对投影图像的相位进行展开，能够得到正确的单周期绝对相位值。

采用红蓝棋盘格作为标定模板，给出了系统的标定方案，并提出基于直线拟合的标定算法，利用Matlab提供的函数对系统进行标定。实验结果表明本文提出的算法具有更高的标定准确度，为后续的三维测量提供了保障。

[1]雷彦章，赵慧洁，姜宏志.一种单双目视觉系统结合的三维测量方法[J].光学学报，2008，28（7）：1338-1342.

[2]Luhmann T，Robson S，Kyle S，et al.Close range photogrammetry：principles，techniques and applications[M]. New York：Wiley&Sons，2006：50.

[3]郑顺义，周漾，黄荣永，等.馆藏文物三维测量与重建方法研究[J].测绘科学，2014，39（7）：76-79.

[4]刘桂华，刘先勇，冯全源，等.大型锻件热态三维结构光在线测量技术[J].光电工程，2010，37（9）：91-97.

[5]何懂，刘晓利，殷永凯，等.结合条纹和伪随机结构光投影的三维成像[J].中国激光，2014，41（2）：0209021.

[6]吕岑，朱欢敏.基于结构光投影的三维指纹特征提取方法[J].科学技术与工程，2014，14（27）：71-74.

[7]魏振忠，张广军，徐园.一种线结构光视觉传感器标定方法[J].机械工程学报，2005，41（2）：210-214.

[8]陈会，密保秀，高志强.基于畸变规律的三维结构光测量系统标定[J].光学学报，2013，33（12）：1215002.

[9]黄燕钧，李中伟，史玉升，等.基于多频外差原理的三维测量技术[J].新技术新工艺，2008（12）：37-40.

[10]陈玲，邓文怡，娄小平.基于多频外差原理的相位解包裹方法[J].光学技术，2012，38（1）：73-78.

Accurate calibration algorithm for structure light system based on line fitting

DONG Jianmin，LI Dongjing
（Shandong Vocational College of Industry，Zibo 256414，China）

An accurate calibration algorithm for projector-camera structure-lighted measuring system has been proposed to improve the accuracy of traditional calibration algorithms.First，find out gray intervals with nearly linear grayscale response.Second，calculate the phase of the projected image by using triple-frequency four-step phase shifting method in the selected interval. Third，extract checkerboard corners from the images captured by the camera，and find out corresponding pixels of these corners in the projector image.Fifth，increase the searching precision of correspondences with the line fitting method.The last step，calibrate the projected structure light system by means of standard stereo.The experiments demonstrate that the proposed algorithm is accurate and satisfies the requirements of three dimensional reconstruction and measurement systems.

three-dimensionalmeasurement；calibration；phase calculation；line fitting

A文章编号：1674-5124（2015）08-0088-06

10.11857/j.issn.1674-5124.2015.08.021

0 引言

近年来，光学三维测量技术被广泛应用于逆向工程、虚拟现实、人体扫描、文物数字化等领域[1-3]。基于结构光的三维重建是一种重要的主动式光学三维测量技术，该方法准确度高、成本低、抗干扰能力强，因而得到了深入的研究[4-6]。随着数字投影技术的不断发展，越来越多的学者开始使用投影仪来投射出固定模式的图像，并搭配普通的工业相机来实现物体的三维测量。

2015-01-01；

2015-03-18

国家863计划资助项目（2011AA040902）

董建民（1979-），男，讲师，硕士，主要从事图像处理、光学测量方面的研究。