基于路面特征系数的路面识别方法研究

张晓龙，孙仁云，刘长伟，葛恒勇

（西华大学交通与汽车工程学院，四川成都610039）

基于路面特征系数的路面识别方法研究

张晓龙，孙仁云，刘长伟，葛恒勇

（西华大学交通与汽车工程学院，四川成都610039）

要使汽车制动时能够充分利用路面的附着条件，需要对当前路面进行识别，同时根据识别结果实时调整系统的目标滑移率。在Burckhardt轮胎-路面模型基础上，引入“路面特征系数”的概念（它表示路面附着系数与附着系数曲线斜率之和），给出7种典型路面的路面特征系数曲线，建立动态识别区间，据此在制动过程中实现路面的动态识别。基于单轮车辆模型进行制动仿真试验，结果表明该方法能够迅速准确地完成路面识别，制动时充分利用路面的附着条件，同时具备自动纠错功能。

路面识别；路面特征；系数；动态；识别区间

目前国内外有大量关于路面识别的研究方法。其中通过μ（s）曲线小滑移率阶段的斜率进行识别的研究最早，但是需要的数据量大，实时性不强[2]；有通过传感器测量路面参数进行路面识别的方法[3]，识别准确率高，但硬件成本高；也有根据路面状态特征值进行的识别[4]，克服了附着系数波动对识别结果的影响，识别准确率高，但对跃变路面的识别有局限性；对车轮振动信号进行小波分析也是一种重要的方法[5-6]，无需准确的轮胎-路面模型，鲁棒性好，但频谱分析量大，实时性不强。

本文提出一种适应性较强的识别方法，以路面特征系数为参数指标，在Burckhardt轮胎-路面模型的基础上建立7种典型路面的动态识别区间，制动时通过实时估算路面特征系数完成路面识别，最后通过计算机仿真验证该方法的可行性。

1 单轮车辆模型

为了简化问题，忽略侧向力、空气阻力以及车轮滚动阻力的影响，假设路面平直，采用单轮车辆模型进行分析[7]，如图1所示。

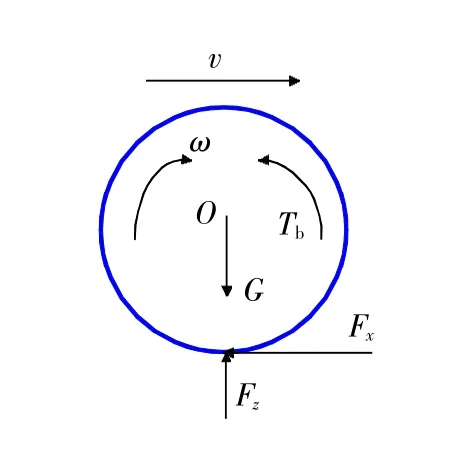
图1 单轮车辆模型

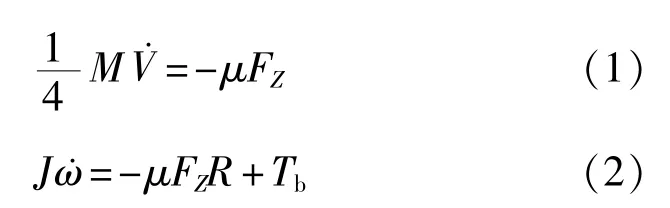
式中：M——车辆的质量；

V˙——车辆的减速度；

μ——路面的附着系数；

FZ——车轮受到来自地面的法向作用力，通过加速度传感器及理论分析可得到；

J——车轮的转动惯量，通常认为是常数；

R——车轮的滚动半径；

ω˙——车轮的角减速度，通过对轮速传感器测得的车轮角速度差分可得到；

Tb——车轮制动器的制动力矩，可根据压力传感器测得的制动轮缸压力进行计算[8]。

2 轮胎模型

Burckhardt等通过大量试验拟合出了各典型路面的μ（s）（附着系数-滑移率）曲线，给出了一个实用的轮胎-路面数学模型，在汽车动力学研究中应用广泛。其表达式[9]如下：

式中c1、c2、c3为各典型路面的参数值，通过求极值的方法求出7种典型路面的最佳滑移率s0，见表1。

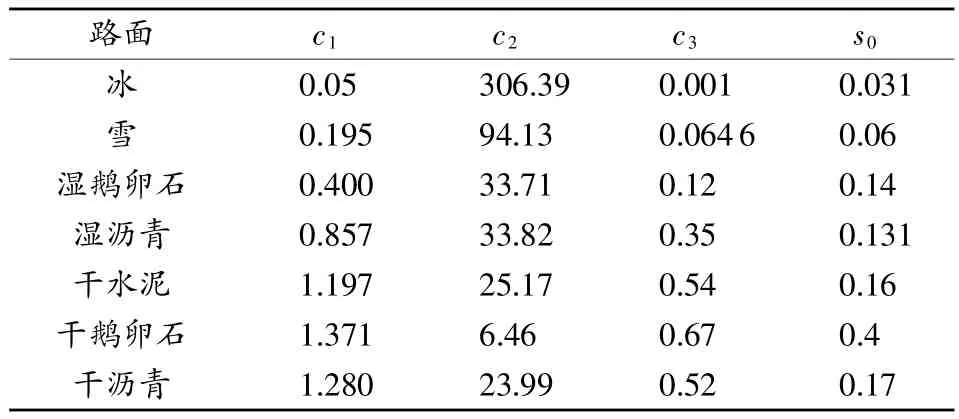
表1 轮胎模型中各典型路面参数值及s0

根据表1中不同路面下c1、c2、c3的值得到7种典型路面的μ（s）曲线，如图2所示，仿真时利用此模型产生路面信号。

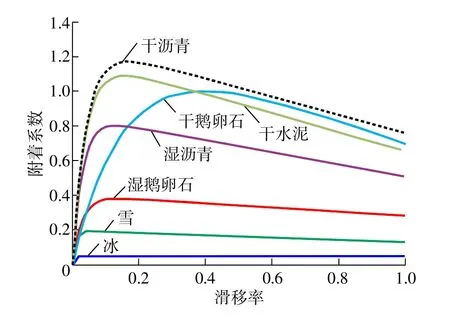
图2 典型路面的μ（s）曲线

图3 典型路面的附着系数曲线斜率-滑移率曲线

3 识别方法

附着系数和附着系数曲线斜率是路面识别最常用的参数指标，虽然对路面附着系数和附着系数曲线斜率的估算方法很多，但最终往往都是将估算值与理论值作比较进行识别。如图2、图3所示，各典型路面的附着系数曲线μ（s）和附着系数曲线斜率μ˙（s）均出现交叉重叠，个别滑移率下不同路面的附着系数或附着系数曲线斜率相等，因此二者单独作为参数指标进行识别时可能出现错误识别。

综合图2、图3可以看出，当不同路面的附着系数相等时其附着系数曲线斜率必然不等，同样当不同路面的附着系数曲线斜率相等时其附着系数必然不等。所以当不同路面的附着系数或附着系数曲线斜率相等时二者之和必然不等。

本文提出“路面特征系数”的概念，并将其作为路面识别的参数指标，其定义如下：

式中：T（s）——路面特征系数；

μ（s）——路面附着系数；

μ˙（s）——附着系数曲线斜率。

3.1 典型路面的动态识别区间

由式（3）微分得：

由式（3）、式（4）、式（5）得：

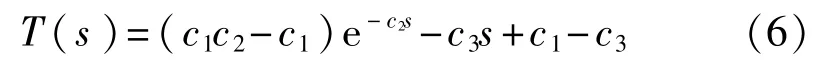
根据式（6）和表1中的参数值得到7种典型路面的T（s）曲线，如图4、图5所示。

当滑移率0.09≤s≤0.50时，各典型路面的T（s）曲线没有出现交叉重叠，差距明显，易于识别。根据各典型路面T（s）曲线的特点建立动态识别区间，即每个滑移率下对应一个识别区间，制动过程中当滑移率变化时，在不同滑移率下系统会对当前路面状态进行反复识别，一旦路面发生跃变或上一个滑移率下出现错误识别，下一时刻滑移率变化后会立即作出正确调整。

图4 路面特征系数-滑移率曲线（0.01≤s≤0.10）

图5 路面特征系数-滑移率曲线（0.10≤s≤0.50）

由于路面的识别区间随着滑移率的变化而变化，这样就绘制出来各路面的识别区间曲线，曲线方程如下：

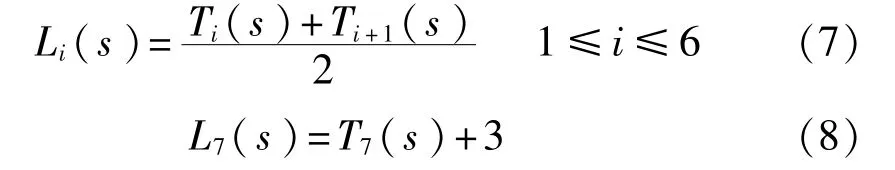
式中：Li（s）——7条识别区间曲线；

Ti（s）——7种典型路面的T（s）曲线。

由式（6）、式（7）、式（8）和表1中的参数值可以计算出各典型路面实时滑移率下对应的识别区间，同时对路面编号，如表2所示。

表2 各典型路面的动态识别区间

3.2 识别算法

如图4、图5所示，当滑移率0.015≤s≤0.5时，冰、雪路面各自与其他6种路面的T（s）曲线没有出现交叉重叠，同时考虑到7种典型路面的最佳滑移率均在区间[0.031，0.4]内，因此实际滑移率应该在区间[0.015，0.5]内变化，所以当滑移率0.015≤s≤0.5时，以T（s）作为参数指标能够在实时滑移率下实现冰、雪路面准确识别。

当滑移率0.015≤s≤0.09时，干鹅卵石、干沥青、干水泥、湿沥青、湿鹅卵石5种路面的T（s）曲线出现交叉重叠，从而导致其识别区间曲线交叉重叠，因此在滑移率区间[0.015，0.09]内通过路面特征系数对这5种路面进行识别时会出现识别错误。考虑到这5种路面的最佳滑移率均大于0.1，因此无论识别结果是5种路面中的哪一个，实时控制的目标滑移率必然大于0.1，这样实际滑移率会迅速向0.1以上递增。当滑移率0.09≤s≤0.5时，5种路面的T（s）曲线不再交叉重叠，同样其识别区间曲线也不再交叉重叠，系统会立即对当前路面作出准确识别。

考虑到车辆绝大部分时间行驶在干沥青路面，因此将目标滑移率的初始值设为0.17，即默认当前路面为路面6。如图4所示，当滑移率＜0.015时，冰、雪路面与干鹅卵石、湿鹅卵石路面的T（s）曲线出现交叉重叠，为了避免将干鹅卵石、湿鹅卵石路面错误识别成冰、雪路面导致目标滑移率骤降，引起识别时间不必要的增加，当滑移率＜0.015时系统不进行识别。

制动过程中如果路面状态发生跃变，当从高附着系数路面跃变为低附着系数路面时，附着系数曲线斜率瞬间无穷小，导致路面特征系数瞬间无穷小；当从低附着系数路面向高附着系数路面跃变时，附着系数曲线斜率瞬间无穷大，导致路面特征系数瞬间无穷大。这两种情况下路面特征系数都超出了7种典型路面的识别区间，因此创建一个虚拟路面，编号为路面8，识别区间为（-∞，0]∪（L7（s），+∞]，路面8的最佳滑移率设为0.2，与7种典型路面均不同，这样一旦路面发生跃变，目标滑移率会调整为0.2，实际滑移率必然出现变化，从而在新的滑移率下完成对跃变路面的正确识别。

3.3 估算路面特征系数

前文定义T（s）的算法中包含对μ（s）和μ˙（s）的估算。因为

所以只要求出附着系数对时间的导数μ˙（t）和滑移率对时间的导数s˙（t），即可求出μ˙（s）。

根据式（2）得：

在已知车轮的角加速度、车轮制动器制动力矩、车轮受到的来自地面的法向作用力等基础上，通过式（10）能够快速估算出当前路面的实时路面附着系数μ。

汽车在实际制动过程中，根据每个车轮动力学参数的估算值都可估算出当前路面的路面特征系数，考虑到汽车制动时载荷发生转移，前轮提供汽车大部分的制动力，因此仅通过前轮进行路面特征系数的估算。当左右前轮的行驶路面不同时，以低附着系数路面的最佳滑移率作为系统的控制目标。

3.4 识别过程

当驾驶员踩下制动踏板后，汽车开始制动，滑移率开始从0向0.17快速递增。当滑移率s=0.015时，系统开始估算当前路面实时滑移率下的路面特征系数T，同时计算实时滑移率下的各路面的识别区间，接着判断路面特征系数T落入哪个对应识别区间，从而完成路面识别，并将识别路面的最佳滑移率作为控制器实时控制的目标滑移率。在整个制动过程中系统不断进行重复识别，一旦前一时刻的识别出现错误或路面发生跃变，下一时刻立即作出调整。

4 仿真试验

在单轮车辆模型的基础上，以30m/s的初速度在跃变路面上进行制动仿真试验。

图6～图9为跃变路面的制动仿真结果。制动开始时预设路面为路面4（湿沥青），2 s后跃变为路面2（雪），3s后跃变为路面5（干水泥）。识别结果如图6所示，由于路面4向路面2跃变时路面特征系数瞬间无穷小，路面2向路面5跃变时路面特征系数瞬间无穷大，所以在2 s、3 s时错误识别出当前路面为路面8（虚拟路面），下一时刻路面特征系数稳定后准确识别出当前路面的路面状态，识别时间几乎为0。如图7所示，在不同路面上制动时，实际滑移率能够快速准确地跟踪当前路面最佳滑移率，控制效果良好。图8为制动力系数-时间曲线，制动过程中制动力系数基本保持在当前路面的峰值附着系数，充分利用了不同路面的附着条件。图9为速度-时间曲线，3.72 s后（车速＜4m/s）ABS系统停止工作，轮速快速下降，3.92 s时车轮抱死，4.29 s时制动完成。在ABS系统工作过程中，车轮没有出现抱死。

综合图6～图9可以看出，制动过程中当路面发生跃变后，系统立即完成当前路面状态的识别，实际滑移率立即跟踪到当前路面的最佳滑移率，确保制动力系数达到当前路面的峰值附着系数，充分利用了不同路面的附着条件，缩短了制动时间和制动距离，提高了制动效能，制动效果良好。

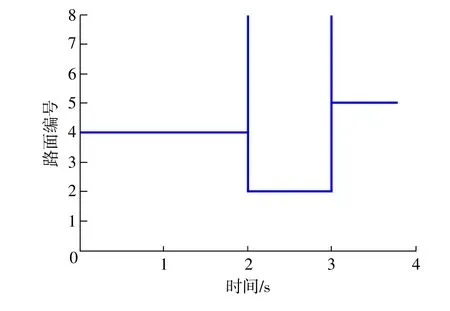
图6 跃变路面识别仿真结果

为了进一步验证该方法对多次跃变路面识别的实时性和准确性，设置一组组合路面，按照（1-2-3-4-5-6-7-1）的顺序每隔0.5s跃变一次，如图10所示，识别结果与预设路面一致，跃变瞬间识别路面均为路面8（虚拟路面），识别时间几乎0。图11为导入误差后的识别仿真结果，分别在0.5 s和2.5 s时导入误差，系统出现错误识别，由于该方法能够在动态识别区间下实现实时识别，下一时刻立即纠正了前一时刻的识别错误，可见该识别方法具备自动纠错功能。

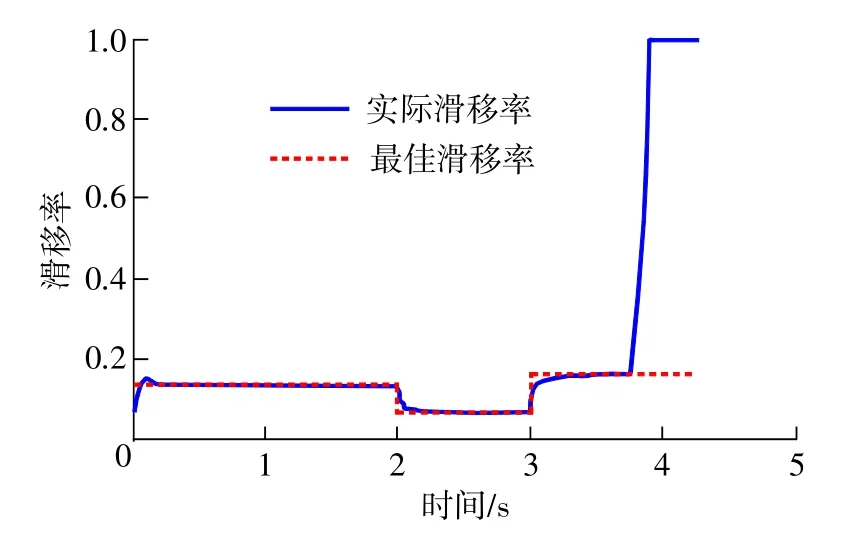
图7 滑移率-时间曲线

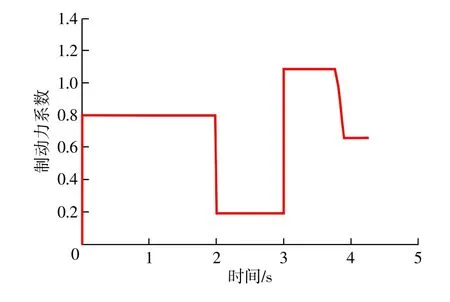
图8 制动力系数-时间曲线

图9 速度-时间曲线

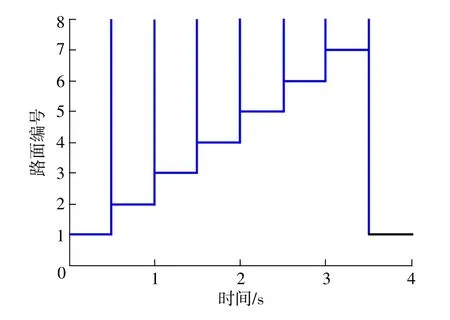
图10 组合路面识别仿真结果

图11 导入误差后的识别仿真结果

5 结束语

1）提出“路面特征系数”的概念，将其作为参数指标进行路面识别时，避免了附着系数或附着系数曲线斜率单独作为识别参数时，附着系数曲线或附着系数斜率曲线交叉重叠对识别的影响，克服了个别滑移率下不同路面参数指标相等带来的不便。

2）根据T（s）曲线特点建立了动态识别区间，每个滑移率下都有对应的识别区间，实现了实时滑移率下的动态识别。同时具备自动纠错功能，一旦出现识别错误，下一时刻会立即纠正。

[1]余志生.汽车理论[M].4版.北京：机械工业出版社，2008：21-29.

[2]Gutafsson F.Slip-based tire-road friction estimation［J］. Auromaricu，1997（33）：1087-1099.

[4]宋健，杨财，李红志，等.AYC系统基于多传感器数据融合的路面附着系数估计算法[J].清华大学学报，2009（5）：101-104.

[5]王博，孙仁云，徐延海，等.考虑路面不平度的路面识别方法[J].机械工程学报，2012（24）：127-133.

[6]卢俊辉，巫世晶.基于车轮振动的路面实时识别研究[J].振动与冲击，2008（4）：19-22.

[7]张晓龙，孙仁云，林小龙，等.基于附着系数曲线长度的路面识别仿真研究[J].湖北汽车工业学院学报，2014，28（2）：1-4.

[8]王博，孙仁云.基于状态特征因子的路面识别方法研究[J].汽车工程，2012，34（6）：506-510.

[9]Burckhardt M.Fahrwerktechnik.Radschlupf-Regelsysteme [M].Wrzburg：VogelVerlag，1993.

A research on road identification based on road characteristic coefficient

ZHANG Xiaolong，SUN Renyun，LIU Changwei，GE Hengyong
（School of Transportation and Automobile Engineering，Xihua University，Chengdu 610039，China）

It is necessary to identify the road surface so as to make full use of its adhesive condition during braking，and accordingly to adjust the target slip ratio in real time.The concept of road characteristic coefficient-the sum of road adhesion coefficient and its gradient-was introduced based on the Burckhardt tyre-road model.Seven typical road characteristic coefficient curves and corresponding dynamic identification intervals were established to identify dynamically the pavement condition during braking.At the same time，brake simulation tests were conducted based on a single-wheel model，and the experimental results show that the method discussed in the paper can quickly and accurately determine road conditions and automatically correct errors.

road identification；road characteristic；coefficient；dynamic；identification interval

A文章编号：1674-5124（2015）08-0031-05

10.11857/j.issn.1674-5124.2015.08.007

0 引言

汽车电控制动系统的核心在于调整路面对轮胎的切向作用力，而该作用力受到路面附着条件的制约，同时路面附着条件又受到滑移率的影响，只有在最佳滑移率下才能最大限度地利用路面的附着条件[1]。但是不同路面的最佳滑移率往往不同，这就需要在制动时对路面状态作出准确识别。

2014-12-04；

2015-02-17

四川省科技厅应用基础项目（2012JY0049）

西华大学人才培养与引进基金项目（R0920301）

西华大学研究生创新基金项目（ycjj2015148）

张晓龙（1988-），男，陕西蒲城县人，硕士，主要从事汽车电控技术研究。