基于混合多样性生成与修剪的集成单类分类算法

刘家辰 苗启广曹 莹 宋建锋 权义宁

(西安电子科技大学计算机学院 西安 710071)

基于混合多样性生成与修剪的集成单类分类算法

刘家辰 苗启广*曹 莹 宋建锋 权义宁

(西安电子科技大学计算机学院 西安 710071)

针对传统集成学习方法直接应用于单类分类器效果不理想的问题，该文首先证明了集成学习方法能够提升单类分类器的性能，同时证明了若基分类器集不经选择会导致集成后性能下降；接着指出了经典集成方法直接应用于单类分类器集成时存在基分类器多样性严重不足的问题，并提出了一种能够提高多样性的基单类分类器混合生成策略；最后从集成损失构成的角度拆分集成单类分类器的损失函数，针对性地构造了集成单类分类器修剪策略并提出一种基于混合多样性生成和修剪的单类分类器集成算法，简称为PHD-EOC。在UCI标准数据集和恶意程序行为检测数据集上的实验结果表明，PHD-EOC算法兼顾多样性与单类分类性能，在各种单类分类器评价指标上均较经典集成学习方法有更好的表现，并降低了决策阶段的时间复杂度。

机器学习；单类分类；集成单类分类；分类器多样性；集成修剪；集成学习

1 引言

单类分类[1](One-class classification)是仅使用一类训练样本建立分类模型的机器学习问题。单类分类仅要求一类样本被有效采样，称为目标类(简称为正类)；其它类由于获取代价过高、无法枚举、采样不充分等原因无法得到有效采样，极端情况下甚至无法获取样本，统称为异常类(简称为负类)。例如，故障诊断中的故障类和人脸检测中的非人脸类等，都是典型的单类分类问题中的负类。单类分类算法通过构建正类的数据描述模型，将其与负类区分，在故障检测[2]、入侵检测[3]、异常检测[4]等应用中取得了良好的效果。

迄今为止，研究者已提出多种单类分类算法，其中支持向量数据描述[5](Support Vector Data Description, SVDD)和单类支持向量机[6](One Class Support Vector Machine, OCSVM)是最流行的两种。单类分类器集成是提升单类分类器性能的有效途径，最初由文献[7]提出，之后的研究者相继将装袋(Bootstrap Aggregation, Bagging)、随机子空间(Random Subspace Method, RSM)和Boosting等集成学习方法用于单类分类算法[810]-。然而以上文献同时指出，传统的集成学习方法应用于单类分类器的表现并不理想，在一些数据集上，集成单类分类器的性能甚至低于单个单类分类器(以下称为基单类分类器)，但造成该问题的原因在现有文献中并没有得到深入分析。

本文首先以概率密度水平集估计模型为基础，推导出集成单类分类器的风险上下界，说明集成单类分类器性能的提升不仅需要基单类分类器集合具有足够的多样性，而且需要精心选择参与集成的基分类器。第二，由于单类分类器集成的多样性问题尚未得到充分研究[11]，本文分析了传统集成方法用于单类分类器集成时存在的多样性不足的问题，并提出了一种混合多样性生成方法提高基单类分类器集合多样性。第三，拆解集成单类分类器的损失函数并分析其构成，提出了一种寻找最优基单类分类器集成顺序的方法。基于以上分析、证明和实验，提出了修剪混合多样性集成单类分类器(Pruned Hybrid Diverse Ensemble One-class Classifier, PHD-EOC)，并通过实验说明PHD-EOC算法能够更有效地提升集成单类分类器的性能。

2 集成单类分类多样性的理论分析

首先给出单类分类问题的形式化描述：

其中X={x|x∈ℜN,i=1,2,…,n}从固定但未

Posii知的分布Q中独立同分布地产生，sign(·)是符号函数，d(x|XPos)是x到目标类XPos的距离度量，d(x | XPos)与阈值θ的差值被用于判定样本x是否属于正类。仅基于该形式化描述并不能有效开展理论分析，这是由于单类分类器必须对负类样本的分布做某种先验假设，否则单类分类问题不可解[12]。常用的假设是负类样本分布的集中程度低于正类样本，故可将单类分类等价于概率密度水平集估计(Density Level Set Estimation, DLSE)，即设在可测空间X中，有已知分布μ(负类样本的分布)和未知分布Q(正类样本的分布)及Q的概率密度h，在给定ρ∈(0,1)时，得到密度函数h上ρ水平集{ρ＜h}的估计。采用文献[12]提出的与以上两种评价具有一致性的概率测度评价指标：

其中s是分布Q和分布μ的平衡参数，()·E表示期望，I(·)是指示函数，指示函数在括号内逻辑表达式成立时取值为1，否则取值为0。对于训练数据集={|∈,i=1,2,…,n}，单类分类的经验风险可以定义为

其中ρ是在DLSE中定义的参数，在单类分类问题中ρ=1-ε,ε是正类拒绝率，即ρ代表正类的接受率。

在式(3)的基础上，假设各基分类器对训练集的n个正类样本均有k个分类错误，对负类样本的分类错误率均为p。记基分类器集合中基分类器个数为T，不失一般性，假设T为奇数。多数投票可能导致的最大风险在每一个错误的集成决策均只由个错误的基分类器决策投票得到，由此得到集成风险的上界为

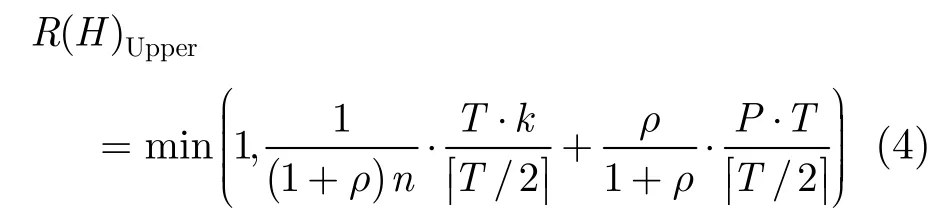
同理，多数投票的最小风险是尽量多的错误投票被包含在正确的集成决策中，因此集成风险的下界为

为直观显示集成风险的上下界，令T=5, ρ=0.9并遍历k和p的可能取值，得到结果如图1所示。

图1中R(H)Upper和R(H)Lower分别表示集成风险的上界和下界，R(H)Mean是基分类器的平均损失。可见虽然集成单类分类器的风险下界随着k和p的降低而降低，但其上界甚至比基单类分类器的平均损失更高。这说明合适的基分类器生成与选取可以降低集成单类分类器的损失，但不合适的基分类器生成与选取可能反而提高单类分类器的损失，因此有必要深入研究基单类分类器的生成与选择方法。

3 PHD-EOC算法

3.1 提升基分类器集合的多样性

以文献[13]为代表的研究者提出了一种混合多样性生成策略，即首先混合使用多种基分类器生成方法生成基分类器集合，再将这些基分类器集成以提高基分类器集合的多样性。本文将该方法引入单类分类器集成，原因如下：第一，单类分类器的原理导致很多原本适用于二分类器的多样性生成方法无法使用，例如纠错输出编码(Error Correcting Output Codes, ECOC)和输出反转(flipping output)等，而混合使用多种多样性生成方法是提升基单类分类器多样性的可行途径；第二，单一集成方法构成集成单类分类器的假设空间受限于具体的基分类器生成方法，而混合使用多种基分类器生成方法可以扩大假设空间；第三，单一集成方法的集成分类器性能提升的大部分由前几个基分类器完成[14]，因此混合使用多种基分类器生成方法能够充分利用每一种集成方法的提升效果。

以下实验使用分类器投影通过将Bagging, RSM和Boosting方法生成的基单类分类器映射到分类器投影空间[15](Classifier Project Space, CPS)中来验证混合多样性生成方法的效果。CPS建立在分类器距离度量，故根据单类分类器的特性，以不一致性度量为基础定义单类分类器ih和jh在数据集X上距离的指标。

UCI数据集①UCI Repository of Machine Learning Databases, http://archive. ics.uci.edu/ml/，访问时间2014年5月10日中Sonar数据上以“Rock”为正类的实验结果如图2所示，其中“TRUE”标记了正确决策参考点的位置，其余各形状的标记表示对应方法生成的基分类器。以“TRUE”标记为圆心绘制圆形参考线，若两个基分类器位于同一参考线上，认为它们性能近似相等。基分类器在CPS空间上欧氏距离小则多样性低，反之多样性高，即基分类器在CPS空间中分布的集中程度越高则多样性越低。从图2(a)，图2(b)和图2(c)中基分类器分布情况可以看出：单一方法生成的基分类器分布集中，多样性较低。而如图2(d)所示，使用不同方法生成的基分类器投影到同一个CPS空间时，生成的基分类器之间明显具有较高的多样性。在多个UCI数据集(参见4.1节列出的UCI数据集)上均可得出类似的实验结果，这些实验说明单一集成方法生成的基分类器集合多样性不足，使用混合多样性生成方法可以有效提高基单类分类器集合的多样性。

图2 几种方法生成基分类器的CPS空间分布图

3.2 修剪集成单类分类器

混合使用多种基分类器生成方法可以提高基分类器的多样性，但单纯提升多样性并不能保证集成单类分类器性能的提升。一种建立在足够多样性基分类器集合基础上的方法是以最终集成分类器的性能为目标选择部分基分类器，即对集成单类分类器进行修剪(Ensemble Pruning，也被称为选择性集成)。修剪步骤不仅能确保单类分类器集成的性能提升效果，有效平衡多样性与性能，也能降低集成分类器的计算复杂度。虽然集成分类器修剪在二分类器上已经取得了一些研究成果[16,17]，但集成单类分类器修剪的研究还是空白。

为此，下面从集成单类分类器损失的角度出发，进一步分析选择基单类分类器的方法。受试者工作特征[18](Receiver-Operating Characteristics, ROC)曲线下包围的面积(Area Under the Curve, AUC)是单类分类研究中最常用的评价指标[1]。从统计特性上讲，AUC与排序问题中的Wilcoxon排序检验等价[18]，因此可定义集成单类分类器的损失函数如下，为书写简便起见以下推导中字面上省略PosX这一符号。

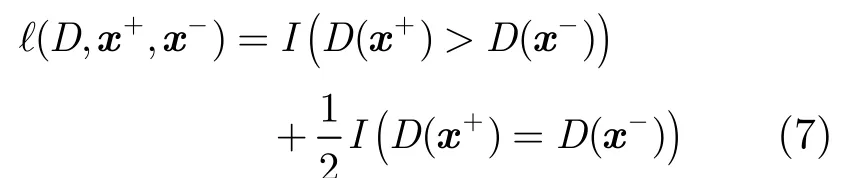
其中x+与x-分别是从正类、负类中随机抽取的样本，函数D是集成单类分类器对样本与目标类之间的距离度量，在采用多数投票时D(x)=(1/T)I(d(x)＞θ)，在此基础上，定义所有基单类i i分类器的平均损失为

为度量集成单类分类器相对于基分类器平均性能的提升程度，计算其损失之差为

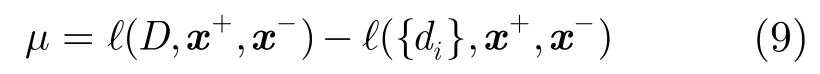
修剪集成单类分类器的目标是选择合适的基单类分类器集合{di}使μ最小化，将式(7)，式(8)代入式(9)并整理，可以得到μ的表达式。

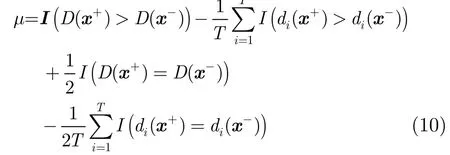
为建立多样性与集成单类分类器修剪的关系，定义某一个基单类分类器与集成分类器的不一致性为

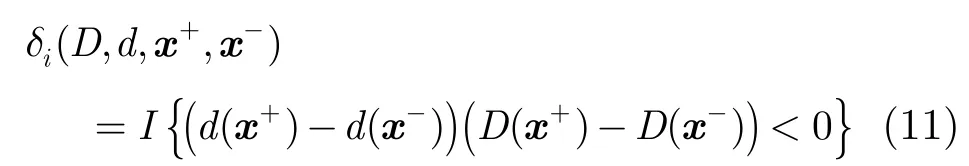
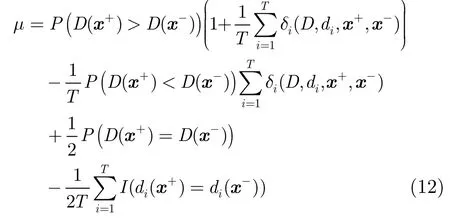
将式(10)依集成分类器决策正确与否的概率展开，同时代入式(11)，可以得到μ与多样性的关系为其中P表示集成分类器决策正确与否的事件概率。式(12)共有4项，其中第3项和第4项出现的概率很低，可以忽略。第1项说明在在集成分类器分类正确时，基分类器的不一致性会增大损失L；第2项说明在集成分类器分类错误时，基分类器的不一致性会减小损失L。据此，可以得到集成单类分类器修剪策略：即尽可能提升集成分类器分类错误时基分类器的多样性，同时避免集成分类器分类正确时基分类器的多样性过高。

从基分类器集合中选择最优基分类器子集是一个NP完全问题[17]，因此假设大小为t的最优基分类器子集总是包含于大小为t+1的最优基分类器子集，从而将该问题转化为寻找最优的基分类器集成顺序[17,19]。根据对式(12)的分析，首先需要得到含有正负类样本的验证样本集，训练数据中缺乏的负类样本可通过人工生成的方法得到[20]，从而得到验证样本集XVal={(xi,yi)|xi∈,i=1,2,…,l,yi∈{-1, 1}}。将验证样本集ValX拆分为被集成分类器正确分类的和被错误分类的。根据对集成分类器分类正确和错误样本多样性的不同要求，从基分类器集合H中选择第k个参与集成的基单类分类器hk的方法为

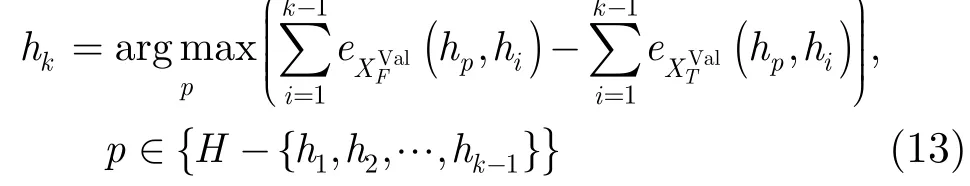
式(13)中的函数eX(hi,hj)如式(6)所定义，该基分类器选择方法能够以式(12)的分析为基础寻找损失最小的基分类器组合。

综合以上分析得到基于多样性的选择性集成单类分类算法PHD-EOC，其流程为：

训练阶段：

(1)采用均匀生成负类样本的方法[21]，得到验证样本集

(2)分别使用M中的各多样性生成方法训练基分类器，得到基分类器集合。

(3)使用H对验证样本集分类，并以分类正确与否为依据将验证样本集拆分为和，即

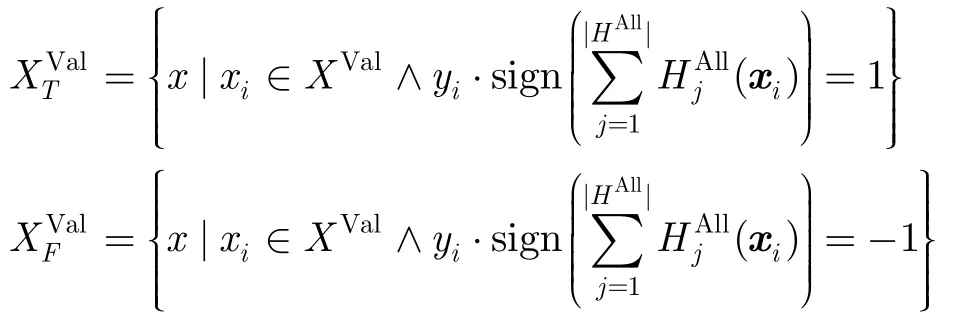
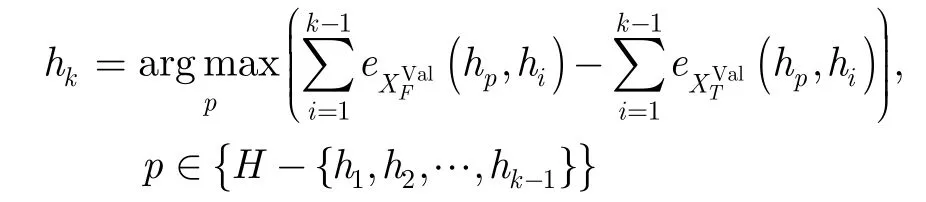
输出：基分类器集合HSel={h1,h2,…,ht}

测试阶段：

分别使用HSel中的基分类器对样本分类，再采用使用多数投票策略即得到PHD-EOC算法的最终决策。

3.3 PHD-ECO算法的时间复杂度分析

记训练样本数为M，假设集成过程中用到的单类分类算法为OCSVM，其训练时间复杂度是O(M3)，决策时间复杂度是O(M)，生成T个基单类分类模型的时间复杂度为T·O(M3)，这是使用Bagging, RSM和Boosting方法集成单类分类算法的训练时间复杂度。与传统集成方法相比，PHD-EOC算法的额外时间消耗是对基分类器的多样性分析和排序过程，其中多样性分析的时间复杂度是T·O(M)，使用快速选择算法选出前γ·T个基分类器的时间复杂度为O(T)。因此PHD-EOC训练阶段的时间复杂度为T·O(M3)+T·O(M)+O(T)≈T·O(M3)，即绝大多数时间复杂度源自基单类分类器的训练时间，因此PHD-EOC相对于传统集成方法的训练阶段时间复杂度提升很小。

在决策阶段，全部基分类器参与集成的决策时间复杂度是T·O(M)，而PHD-EOC算法的决策时间复杂度是γ·T·O(M)，决策阶段时间复杂度有较大降低，降低的程度取决于基分类器选择比率γ。

4 实验结果与分析

4.1 标准数据集实验

为验证PHD-EOC算法的有效性，将其与选择传统集成学习方法进行对比。实验程序使用MATLAB r2012b编写，基分类器中OCSVM使用LIBSVM[22]提供的算法实现，NegSVDD算法通过修改LIBSVM实现。

实验中选择Bagging, RSM方法和Boosting这3种最常用的集成学习方法作为对比算法。由于并没有广泛认可地特别针对单类分类问题的标准数据集，单类分类研究通常使用UCI数据集的二分类数据集，并指定两类中样本较多的一类为正类[1]。实验从UCI数据集中选择了单类分类研究常用的Biomed, Breast, Diabetes, Ecoli, Heart, Hepatitis, Imports, Sonar, Spectf和Wine等10个数据集构成11个单类分类数据集，其中Sonar数据集在使用传统集成单类分类器时效果较差[8,9]，故以其两类分别为正负类形成了两个单类分类数据集。

实验采用二迭交叉验证重复10次取平均值，使用OCSVM算法作为基分类器生成算法，其中正类拒绝率设置为0.1。OCSVM使用常用的RBF核函数，核函数中关键的参数核带宽使用二迭交叉验证的网格搜索得到，搜索范围是{2k}，其中k取[-10,10]内的整数，实验过程为：

步骤1 分别按照Bagging, RSM和Boosting各自的基分类器生成方法，各得到90个基单类分类器并按照各自的集成方式集成，分别记为“Bagging”,“RSM”和“Boosting”。同时，从3种方法的基分类器集合中各抽取前30个基分类器，这些基分类器多数投票得到的集成单类分类器记为“ALL”。

步骤.2 使用PHD-EOC算法，分别取选择率γ为0.2, 0.4和0.6，修剪步骤3得到的集成单类分类器，将得到的集成单类分类器模型分别记为“PHDEOC(γ=0.2)”,“PHD-EOC (γ=0.4)”和“PHDEOC (γ=0.6)”。

步骤3 评估前两个步骤得到的7个集成单类分类器，分别比较它们的AUC, F指标(F-measure，取1α=，记为F1)和G指标(G-measure，取1α=，记为G1)，完整的对比实验结果如表1所示。

从表1给出的实验结果中可以看出：

(1)在基分类器个数相等的前提下，混合使用多种方法生成基分类器集合也可以有效地提高集成基单类分类器的性能。但在一些数据集上“ALL”和RSM等单一方法的性能并无明显差距，这说明了单独使用混合多样性生成策略提高多样性是不够的，需要通过PHD-EOC算法的修剪步骤提高集成单类分类器性能。

(2)PHD-EOC算法的AUC, F-measure和G-means指标明显优于Bagging, RSM, Boosting和“ALL”算法，说明选择性集成确实能够在降低参与集成基分类器个数的同时，提高集成单类分类器的性能。

(3)修剪步骤的最优选择率γ因数据集而异，但实验结果表明在基分类器个数相同的情况下，经过PHD-EOC排序后的集成分类器性能几乎总是优于随机顺序集成。

为说明基分类器集成顺序对集成分类器性能的影响，将PHD-EOC算法和随机顺序集成的“ALL”算法的迭代性能曲线对比如图3所示。在迭代过程中，PHD-EOC算法的迭代AUC指标几乎始终优于随机集成顺序的“ALL”集成分类器，说明依照多样性分析得到的集成顺序能够有效提升集成单类分类器的性能。

表1 UCI数据集上的对比实验结果

4.2 恶意程序检测实验

本节通过将PHD-EOC算法用于计算机安全领域中恶意程序行为检测来进一步评估其在实际应用问题中的表现。在恶意程序检测问题中，正常程序种类繁多，功能各异，收集样本的难度很大，而恶意程序行为具有普遍的相似性，并且可以从一些专门的网站批量获取，容易得到数量较大的恶意程序样本集。因此正常程序类样本很难被视为整个正常程序类别的充分采样。单类分类模型不对负类样本的采样情况做任何要求，因此将正常程序类作为负类更符合样本特性，并有效降低误检率。实验采用实验室自主开发的Osiris系统[23]捕获到的程序行为数据，每个恶意程序样本以2488维的离散值特征表示。数据集包含3155个正常程序样本和15263个恶意程序样本。其中正常程序样本采用恶意程序分析研究中通行的做法收集自全新安装的Windows 7操作系统，恶意程序从VX-Heaven②VX-Heaven, http://vxheaven.org，访问时间2014年5月10日公开的恶意程序数据库以及MLSEC③Machine Learning for Computer Security, http://www.mlsec.org，访问时间2014年5月10日研究组提供的样本中收集整理，包含后门、蠕虫、Rootkit、木马和病毒等常见类别的65个重要恶意程序家族，包含了主要恶意程序类别和各类别中典型的恶意程序家族，具有较充足的覆盖能力，能够代表绝大多数恶意程序。

图3 PHD-EOC算法和随机集成顺序的集成单类分类器迭代AUC变化曲线

从表2中的实验结果可以看出：首先，3种经典集成方法中RSM方法和Bagging方法效果较Boosting方法效果略好，这是因为恶意程序行为数据中存在较多难以手工去除的噪声，对噪声敏感的Boosting方法性能造成了一定影响。其次，混合多样性生成的“ALL”算法较Bagging, RSM和Boosting等单一集成算法性能更优，该结果与之前分析和实验的结果一致，进一步验证了提升基分类器集多样性能够提高集成单类分类器的性能。最后，PHD-EOC算法在多数情况下取得了比“ALL”更优的性能，这验证了经过修剪的集成单类分类器的性能优势。此外，选择适中的选择率γ能够取得较好的集成单类分类器修剪结果。

表2 PHD-EOC算法在恶意程序行为检测数据集上的实验结果

由以上实验分析可知，PHD-EOC算法的性能普遍优于其他集成单类分类算法，进一步验证了PHD-EOC算法在较复杂的实际问题中的有效性，说明PHD-EOC算法具有较大的推广应用价值。

5 结束语

本文首先证明了单类分类器集成的性能提升效果，也指出不经选择的集成可能带来的风险。通过实验分析了传统集成方法在单类分类器集成中存在的多样性不足是制约其性能的主要原因，证明了修剪步骤对集成单类分类器的作用，同时通过拆解集成损失得到了具体的修剪策略。在以上证明和分析的基础上提出了PHD-EOC算法，该算法通过混合多样性生成方法得到多样性强的基单类分类器集合，之后通过分析基分类器多样性与集成性能提升之间的关系，选择一部分基分类器参与集成，在标准数据集和实际恶意程序检测数据上的实验结果表明，PHD-EOC算法能够得到性能优于将全部基分类器集成的集成单类分类器。

[1] Tax D. One-class classification[D]. [Ph.D. dissertation]. Delft University of Technology, 2001.

[2] Xiao Ying-chao, Wang Huan-gang, Zhang Lin, et al.. Two methods of selecting Gaussian kernel parameters for one-class SVM and their application to fault detection[J]. Knowledge-Based Systems, 2014, 59(1): 75-84.

[3] Mennatallah A, Markus G, and Slim A. Enhancing one-class support vector machines for unsupervised anomaly detection[C]. Proceedings of the ACM SIGKDD Workshop on Outlier Detection and Description, Chicago, USA, 2013: 8-15.

[4] Shahid N, Naqvi I, and Qaisar S. One-class support vector machines: analysis of outlier detection for wireless sensor networks in harsh environments[J]. Artificial Intelligence Review, 2013, 39(1): 1-49.

[5] Tax D and Duin R. Support vector data description[J]. Machine Learning, 2004, 54(1): 45-66.

[6] Schölkopf B, Platt J, Shawe-Taylor J, et al.. Estimating the support of a high-dimensional distribution[J]. Neural Computation, 2001, 13(7): 1443-1471.

[7] Tax D and Duin R. Combining one-class classifiers[C]. Proceedings of 2nd International Workshop on Multiple Classifier Systems, Cambridge, UK, 2001: 299-308.

[8] Segui S, Igual L, and Vitria J. Bagged one-class classifiers in the presence of outliers[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2013, 27(5): 1-21. [9] Cheplygina V and Tax D. Pruned random subspace method for one-class classifiers[C]. Proceedings of the 10th International Conference on Multiple Classifier Systems, Naples, Italy, 2011: 96-105.

[10] Ratsch G, Mika S, Scholkopf B, et al.. Constructing boosting algorithms from SVMs: an application to one-class classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(9): 1184-1199.

[11] Aggarwal C. Outlier ensembles: position paper[J]. ACM Special Interest Group on Knowledge Discovery and Data Mining (SIGKDD) Explorations Newsletter, 2013, 14(2): 49-58.

[12] Steinwart I, Hush D, and Scovel C. A classification framework for anomaly detection[J]. Journal of Machine Learning Research, 2006, 6(1): 211-232.

[13] Caruana R, Niculescu-Mizil A, Crew G, et al.. Ensemble selection from libraries of models[C]. Proceedings of 21st International Conference on Machine Learning, Banff, Canada, 2004: 137-144.

[14] Kotsiantis S. Combining bagging, boosting, rotation forest and random subspace methods[J]. Artificial Intelligence Review, 2011, 35(3): 223-240.

[15] P kalska E, Duin R, and Skurichina M. A discussion on the classifier projection space for classifier combining[C]. Proceedings of 3rd International Workshop on Multiple Classifier Systems, Cagliari, Italy, 2002: 137-148.

[16] Guo L and Boukir S. Margin-based ordered aggregation for ensemble pruning[J]. Pattern Recognition Letters, 2013, 34(6): 603-609.

[17] Martinez-Muoz G, Hernández-Lobato D, and Suárez A. An analysis of ensemble pruning techniques based on ordered aggregation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 245-259.

[18] Fawcett T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861-874.

[19] Tamon C and Xiang J. On the boosting pruning problem[C]. Proceedings of 11th European Conference on Machine Learning, Catalonia, Spain, 2000: 404-412.

[20] Désir C, Bernard S, Petitjean C, et al.. One class random forests[J]. Pattern Recognition, 2013, 46(12): 3490-3506.

[21] Tax D and Duin R. Uniform object generation for optimizing one-class classifiers[J]. The Journal of Machine Learning Research, 2001, 2(1): 155-173.

[22] Chang C and Lin C. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 1-27.

[23] Cao Ying, Liu Jia-chen, Miao Qi-guang, et al.. Osiris: a malware behavior capturing system implemented at virtual machine manage layer[C]. Proceedings of 8th International Conference on Computational Intelligence and Security, Guangzhou, China, 2012: 534-538.

刘家辰： 男，1988年生，博士生，研究方向为机器学习与计算机安全.

苗启广： 男，1972年生，教授，博士生导师，研究方向为智能图像处理与机器学习.

曹 莹： 女，1987年生，博士生，研究方向为机器学习.

宋建锋： 男，1978年生，讲师，研究方向为计算机安全与机器学习.

权义宁： 男，1968年生，副教授，研究方向为网络计算与网络安全.

Ensemble One-class Classifiers Based on Hybrid Diversity Generation and Pruning

Liu Jia-chen Miao Qi-guang Cao Ying Song Jian-feng Quan Yi-ning
(School of Computer Science and Technology, Xidian University, Xi’an 710071, China)

Combining one-class classifiers using the classical ensemble methods is not satisfactory. To address this problem, this paper first proves that though one-class classification performance can be improved by a classifier ensemble, it can also degrade if the set of base classifiers are not selected carefully. On this basis, this study further analyzes that the lacking of diversity heavily accounts for performance degradation. Therefore, a hybrid method for generating diverse base classifiers is proposed. Secondly, in the combining phase, to find the most useful diversity, the one-class ensemble loss is split and analyzed theoretically to propose a diversity based pruning method. Finally, by combining these two steps, a novel ensemble one-class classifier named Pruned Hybrid Diverse Ensemble One-class Classifier (PHD-EOC) is proposed. The experimental results on the UCI datasets and a malicious software detection dataset show that the PHD-EOC strikes a better balance between the diverse base classifiers and classification performance. It also outperforms other classical ensemble methods for a faster decision speed. Key words: Machine learning; One-class classifier; Ensemble One-class Classifier (EOC); Classifier diversity; Ensemble pruning; Ensemble learning

TP181

A

1009-5896(2015)02-0386-08

10.11999/JEIT140161

2014-01-24收到，2014-06-03改回

国家自然科学基金(61272280, 41271447, 61272195)，教育部新世纪优秀人才支持计划(NCET-12-0919)，中央高校基本科研业务费专项资金(K5051203020, K5051303016, K5051303018, BDY081422, K50513100006)和西安市科技局项目(CXY1341(6))资助课题

*通信作者：苗启广 qgmiao@gmail.com