基于线阵的MIMO-ISAR二维成像方法

董会旭张永顺 冯存前 李 哲

(空军工程大学防空反导学院 西安 710051)

基于线阵的MIMO-ISAR二维成像方法

董会旭*张永顺 冯存前 李 哲

(空军工程大学防空反导学院 西安 710051)

针对多输入多输出逆合成孔径雷达(MIMO-ISAR)成像中空-时阵列非均匀造成的成像数据不均匀，该文基于线阵建立了目标空-时回波信号模型，经过推导，提出一种相同距离单元横向聚焦的成像方法。该方法首先进行距离补偿，将空时分布的距离像对齐至目标初始位置；然后构建相位因子，补偿非关心方向运动引起的相位变化；最后对相同距离单元数据沿横向相干叠加，实现横向聚焦。该算法不受阵列形式的限制，无需数据均匀化处理，而且能够横向定标，仿真验证了该方法的有效性。

多输入多输出逆合成孔径雷达成像；距离补偿；横向聚焦

1 引言

多输入多输出逆合成孔径雷达(MIMO-ISAR)成像是近年来提出的一种新型成像技术，它结合MIMO雷达技术与ISAR成像技术的优点，将成像所需的阵列孔径长度在时间和空间上合理分配。因此，相对于传统的ISAR成像方法，在保持分辨力不变的情况下，积累时间减小为原积累时间的1/()MN[1](,MN为收发阵元个数)；相对于MIMO雷达成像和实孔径雷达成像又可以大大减少阵元规模。由于积累时间的大幅减少，目标运动得到简化，因而其在解决复杂运动目标的成像方面具有一般ISAR成像雷达所不具备的独特优势；由于阵元规模的减小，相比MIMO雷达，MIMO-ISAR对波形设计以及阵列结构的要求大大降低[2,3]。因此，MIMOISAR已经成为雷达成像领域新的研究热点[410]-。

对于MIMO-ISAR成像，文献[1,2]通过重排和插值的方法对非均匀的成像数据均匀化，然后用距离-多普勒(Range-Doppler, R-D)算法实现2维成像，验证了MIMO-ISAR的可行性；文献[4]提出了一种特殊的阵列结构，根据相位近似(Phase Center Approximation, PCA)原理，MIMO等效阵列近似为均匀面阵，并提出空时信号联合处理方法，实现了MIMO-ISAR 3维成像；文献[5]在建立MIMO雷达3维成像的信号模型的基础上，分析了对阵列结构、强散射点选择准则以及信号发射策略等，实现了MIMO雷达单次快拍成像；文献[6]在文献[5]的研究基础上，讨论了 MIMO-ISAR 成像时所需的图像校正和目标速度估计，提出利用MIMO-ISAR对目标3维成像，并给出了MIMO-ISAR成像的数据重排与运动补偿方法；文献[7]则采用MIMO技术的侧视多掠ISAR，增强了雷达成像的方位分辨率；文献[8]研究了空时不等效对成像质量的影响，得到计算成像结果中虚假目标数量及其位置的数学公式，给出了目标与最大假目标的幅度比值；文献[11]提出了一种极坐标下的成像方法，该方法首先将极坐标格式下的非均匀MIMO-ISAR成像数据降维，然后通过插值运算转化为直角坐标系下的均匀数据进行成像；文献[12]给出了地基MIMO-SAR对金属点目标的成像方法，并进行了外场的实验验证；文献[13]给出了一种基于尺度变换的虚拟孔径成像算法。

在研究MIMO-ISAR成像的过程中，本文发现：(1)采用R-D算法成像要求数据均匀，需使用空时等效和阵列内插进行数据重排和填充，成像过程复杂，运算量大；(2)复杂的数据结构给现有运动补偿算法带来困难；(3)利用PCA原理得出MIMO雷达阵列的等效虚拟阵元位置，等效误差补偿不可忽略[8,9]。针对上述问题，本文建立了基于线阵的MIMOISAR空时信号模型，通过推导，提出一种相同距离单元数据横向聚焦的成像方法，该方法不受阵列形式的限制，无需数据重排和阵列内插运算，而且可以对目标散射点横向定标。另外，本文算法没有使用PCA原理近似等效阵元位置，无需相位等效误差补偿。

本文安排如下：第2节建立MIMO-ISAR空时信号模型；第3节提出一种同距离单元数据横向聚焦的MIMO-ISAR成像方法；第4节为仿真验证及分析；第5节为全文结论。

2 信号模型

MIMO-ISAR成像几何模型如图1所示，发射阵元和接收阵元分布在Y轴上，本文采用线阵的参数为：发射阵元数为M，间距为dt；接收阵元数为N，间距为dr，且dt=Ndr；发射阵列与接收阵列间隔为dtr。3维空间目标运动速度矢量V=(Vx, Vy,Vz)，P为目标上任意一散射点，初始坐标为(x,y,z)，目标的参考中心为(x0,y0,z0)。

那么，P点与发射、接收阵元的瞬时斜距可以表示为

图1 MIMO-ISAR成像几何模型

式中，R(m,ta)为ta时刻P点与第m个发射阵元的瞬时斜距，R(n,ta)为为ta时刻P点与第n个接收阵元的瞬时斜距；d(m),d(n)(m=1,2,…,M,n=1, 2,…,N)分别表示发射、接收阵元的坐标；g(ta), L(ta),h(ta)则表示目标在X,Y,Z坐标轴方向上随慢时间ta的运动。

MIMO-ISAR雷达发射M个相互正交的同频宽带信号，一般选用相位编码信号，设第m个发射阵元的相位编码信号[14]为

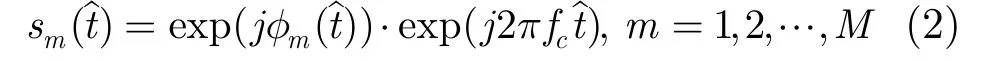
这组相位编码信号满足：

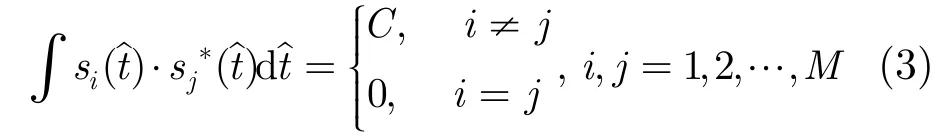
即表示相位编码信号在时域相互正交，C为非零常数。

假设目标上有P个散射点，散射系数为pξ, p=1,2,,P…。那么，去载频的目标回波信号为

通常目标的运动速度远小于电磁波在空气中的传播，且径向速度更小；另外，雷达信号的脉冲持续时间也很短，因此，在雷达一次探测期间，近似认为目标静止，忽略多普勒对回波的影响，即此时目标运动采用停-走(stop-go)模型；那么，

回波信号经过匹配滤波器组之后，单次快拍回波分选为MN路信号：

因此，全时间上接收阵元可以获得MN×A个距离像数据，数据结构如图2所示，成像数据分布在空时2维。由于目标非合作，因而空时数据相互之间采样间隔并不确定，造成数据结构非常复杂。若仍然按照传统ISAR成像方法，必须对数据重排和均匀化填充；另外，还需要新的平动补偿方法。

图2 MIMO-ISAR 1维像数据示意图

由于这MN×A个距离像数据都具有图钉状的波形，主瓣高度与宽度都完全相同，只是在旁瓣上有细微的差别，因而可做近似sm)≈), ∀m[9]。那么，式(5)可改写为

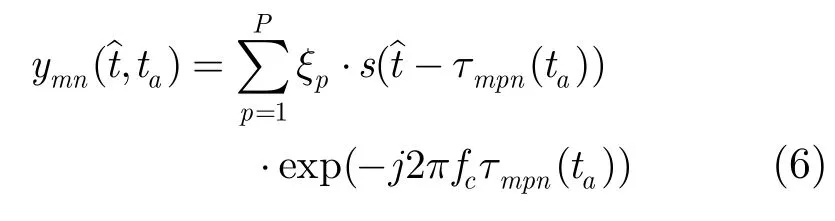
3 成像算法

由于MIMO-ISAR成像中积累时间很短，目标的运动可以用一阶运动近似[1]，那么由式(1)可得第p个散射点在慢时间上相对于收发阵元的斜距：

由菲涅尔近似可得

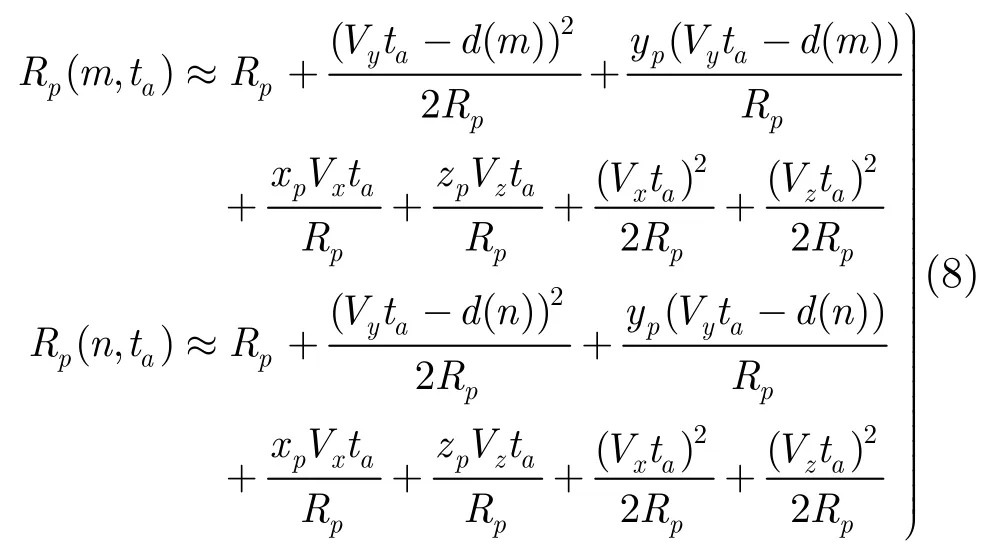
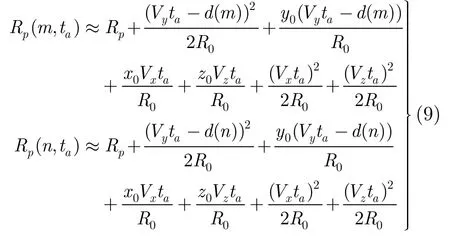
假设目标位置、速度估计已完成，则由式(9)可以构建距离补偿因子ψ(d(m),d(n),ta)，将所有散射点距离至Rp，

其中

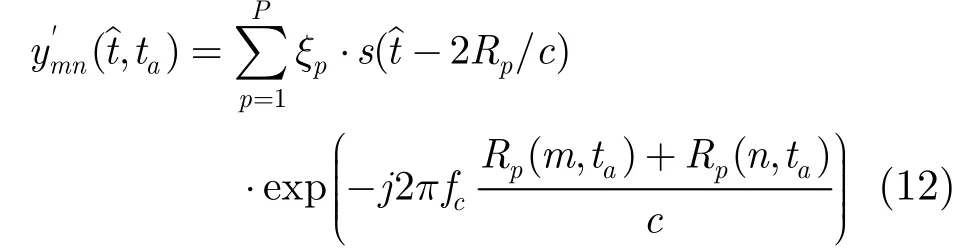
式(12)中各散射点的时延校正为2Rp/c，与空间阵元位置以及时间合成阵元位置都无关，那么只需对目标成像区域进行横向(Y方向)划分，然后按距离单元进行聚焦处理，对每个距离单元的散射点实现横向分辨。

由上述对目标运动分析可知，目标除了横向运动还有X方向和Z方向运动，因此在进行横向分辨之前，必须要对其影响进行补偿。由式(7)近似有

由于每个空间阵元Y方向都相同且运动时间很短，运动分量远小于散射点到收发阵列斜距，因此，式(13)二次项可忽略，px,pz,pR可以用0x,0z,0R代替。一阶假设下，目标速度在y坐标轴的分量为常数，虽不会引起成像结果散焦，但会造成2维像偏出成像场景区域。那么，可构建相位补偿因子为

假设距离像的采样数为K，方位向采样数为L，则距离像的采样点可表示为rk(k=1,2,…,K)，方位向的采样点可表示为yl(l=1,2,…,L)。计算像素点(rk,yl)相对于收发阵元的时延：

那么，目标最终的聚焦成像的结果为

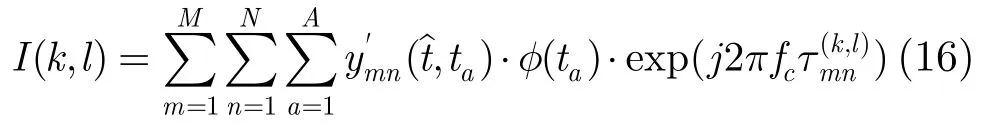
综上所述，MIMO-ISAR的成像过程示于图3。从图3可见，本文算法较之R-D算法处理过程更简单，运动补偿更容易，鲁棒性强。

图3 MIMO-ISAR成像过程

4 仿真

参数设置：仿真采用3发4收MIMO阵列，发射阵元坐标为(-300,0,0), (-180,0,0), (-60,0,0)；接收阵元坐标(60,0,0), (90,0,0), (120,0,0), (150, 0,0)。目标由9个散射点组成，位置图如4所示，图4(a)为散射点在3维空间中的位置，图4(b)为目标在X-Y平面的投影。从目标中心到阵列中心的斜距R0设为10000 m，目标做匀速直线运动，速度为300 m，速度与x,y,z轴的夹角分别为70°, 20°, 0°。

设置雷达参数如表1，根据本文所提成像方法，MATLAB仿真得出成像结果如图5所示。

图5 为信噪比为3 dB时的仿真结果。分析图5，图5(a)为距离补偿后的成像数据，此时目标的成像数据都对准至目标散射点在空间坐标系中的初始位置，验证了距离补偿的有效性。图5(b)为本文方法的最终成像结果，在X, Z方向运动相位补偿之后，通过横向聚焦在场景中心位置得到目标的2维像，验证了成像方法的有效性。图5(c)为MIMO-ISAR通过数据均匀化处理之后R-D算法成像结果，图5(b)，图5(c)的图像熵分别为3.6318, 4.3655，可见本文方法的成像质量比传统方法更好。

表1 雷达参数

图4 目标散射点位置图

图5 SNR=3 dB时仿真结果

另外，本文方法在得出目标2维像的同时，还可以实现目标像的横向定标；图5(b)的横坐标变量就是目标实际的横向坐标值而不是传统ISAR中的目标转动多普勒，本文方法所得2维像无需单独进行横向定标，只需谱峰搜索即可得出目标的横向坐标值。定标结果如表2所示，由表2可知，定标值与真实坐标值之间最大误差为0.1 m。

表2 横向定标值与真实值

5 结束语

本文首先分析了MIMO-ISAR成像几何关系，建立了MIMO-ISAR成像信号模型，指出了MIMOISAR成像的难点以及现有MIMO-ISAR成像方法存在的不足，然后提出一种相同距离单元数据横向聚焦的成像方法，该方法避免了成像中的插值、等效阵元误差补偿等运算，同等条件下较之传统R-D算法成像质量更好，而且还能够对目标像横向定标，仿真试验结果证明了方法的有效性。

[1] 朱宇涛, 郁文贤, 粟毅. 一种基于MIMO技术的ISAR成像方法[J]. 电子学报, 2009, 37(9): 1885-1894. Zhu Yu-tao, Yu Wen-xian, and Su Yi. An ISAR imaging method based on MIMO technique[J]. Acta Electronica Sinica, 2009, 37(9): 1885-1894.

[2] Zhu Yu-tao, Su Yi, and Yu Wen-xian. An ISAR imaging method based on MIMO technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(8): 3290-3299.

[3] Zhuge X D and Yarovoy A G. Three-dimensional near-field MIMO array imaging using range migration techniques[J]. IEEE Transactions on Image Processing, 2012, 21(6): 3026-3033.

[4] 朱宇涛, 粟毅. 一种M2发N2收MIMO雷达平面阵列及其三维成像方法[J]. 中国科学F辑, 2011, 41(12): 1495-1506. Zhu Yu-tao and Su Yi. A type of M2-transmitter N2-receiverMIMO radar rrray and 3D imaging theory[J]. Science China Information Sciences, 2011, 41(12): 1495-1506.

[5] Ma Chang-zheng, Yeo T S, Tan C S, et al.. Threedimensional imaging of targets using colocated MIMO radar[J]. IEEE Transactions on Geoscince and Remote Sensing, 2011, 49(8): 3009-3021.

[6] Ma Chang-zheng, Yeo T S, Tan C S, et al.. Threedimensional imaging using colocated MIMO radar and ISAR technique[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3189-3201.

[7] Bucciarelli M and Pastina D. Multi-grazing ISAR for side-view imaging with improved cross-range resolution[C]. Processings of the 2011 IEEE Radar Conference, Kansas City, USA, 2011: 939-944.

[8] 陈刚, 顾红, 苏卫民, 等. 空时不等效对MIMO雷达采用ISAR技术成像影响的分析[J]. 电子与信息学报, 2013, 35(8): 1806-1812. Chen Gang, Gu Hong, Su Wei-min, et al.. Analysis on the effect of nonequivalent relationship between space and time in MIMO-ISAR imaging[J]. Journal of Electronics & Information Technology, 2013, 35(8): 1806-1812.

[9] 王怀军, 朱宇涛, 许红波, 等. MIMO雷达等效相位中心误差分析[J]. 电子与信息学报, 2010, 32(8): 1849-1854. Wang Huai-jun, Zhu Yu-tao, Xu Hong-bo, et al.. Analysis of displaced phase center error in MIMO radar[J]. Journal of Electronics & Information Technology, 2010, 32(8): 1849-1854.

[10] 陈刚, 顾红, 苏卫民. MIMO雷达最小冗余垂直阵列设计方法[J]. 空军预警学院学报, 2013, 27(2): 79-82. Chen Gang, Gu Hong, and Su Wei-min. Design of minimum redundancy vertical array for MIMO radar[J]. Journal of Air Force Early Warning Academy, 2013, 27(2): 79-82.

[11] 陈刚, 顾红, 苏卫民. 采用ISAR技术的MIMO雷达极坐标格式成像算法研究[J]. 宇航学报, 2013, 34(8): 1137-1145. Chen Gang, Gu Hong, and Su Wei-min. Research on polar format imaging algorithm for MIMO radar based on ISAR technique[J]. Journal of Astronautics, 2013, 34(8): 1137-1145.

[12] Tarchi D, Oliveri F, and Sammartino P F. MIMO radar and ground-based SAR imaging systems: equivalent approaches for remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 425-435.

[13] 王海青, 李彧晟, 朱晓华. 基于快速极坐标格式算法的MIMO雷达虚拟孔径成像[J]. 宇航学报, 2013, 34(5): 715-720. Wang Hai-qing, Li Yu-sheng, and Zhu Xiao-hua. MIMO radar virtual aperture imaging based on fast polar format algorithm[J]. Journal of Astronautics, 2013, 34(5): 715-720.

[14] Hai Deng. Poly phase Code design for orthogonal netted radar systems[J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3126-3135.

[15] 朱宇涛. 多通道ISAR成像技术研究[D]. [博士论文], 国防科学技术大学, 2011. Zhu Yu-tao. Multiple-channel ISAR imaging[D]. [Ph.D. dissertation], National University of Defense Technology, 2011.

董会旭： 男，1987年生，博士生，研究方向为雷达成像新技术.

张永顺： 男，1961年生，教授，博士生导师，研究方向为雷达信号处理和综合电子战.

冯存前： 男，1975年生，副教授，硕士生导师，研究方向为雷达成像与微动特征提取.

Two-dimensional Imaging Using MIMO Radar and ISAR Technique Based on Linear Array

Dong Hui-xu Zhang Yong-shun Feng Cun-qian Li Zhe
(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)

In view of the uneven imaging data caused by the uneven space-time array in the MIMO-ISAR imaging, the echo signal model of a target is established based on a linear array, an imaging algorithm that focuses on the cross-range direction following range unit is proposed. The range compensation is applied firstly, which can make range profiles that distribute in the space-time domain align at the initial position of target. Then phase changes caused by motion in unconcerned direction are compensated. Finally, the range profiles are focused in the cross-range direction following range unit by coherent addition. The algorithm is not restricted by the structure of the array and the processing of uniformity is not needed. In addition, it can determine the ISAR image scale in the cross-range direction. The simulation results verify the validity of the proposed algorithm.

MIMO-ISAR imaging; Range compensation; Focusing in the cross-range direction

TN 958

A

1009-5896(2015)02-0309-06

10.11999/JEIT140529

2014-04-24收到，2014-07-03改回

国家自然科学基金(61382166)和陕西省自然科学基础研究计划(2014JM8308)资助课题

*通信作者：董会旭 dx19871109@163.com