基于幅相一致性校正的稳健植被参数反演方法

卢红喜宋文青李 飞王英华刘宏伟保 铮黄海风

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

②(国防科学技术大学电子科学与工程学院 长沙 410073)

基于幅相一致性校正的稳健植被参数反演方法

卢红喜*①宋文青①李 飞①王英华①刘宏伟①保 铮①黄海风②

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

②(国防科学技术大学电子科学与工程学院 长沙 410073)

植被参数反演是极化干涉合成孔径雷达(PolInSAR)的重要应用。传统反演方法未考虑观测样本数据幅度和相位的非平稳特性，以及观测信号非均匀分布对其散布区域线性变化主导方向估计的影响。针对这些问题，该文首先采用经过幅度和相位一致性校正的数据样本估计极化相干矩阵，提高了极化干涉复相干系数的估计性能，并提出了映射空间均衡化(MSR)处理技术以消除观测信号非均匀分布对主导方向提取的影响，通过引入主成分分析(PCA)方法进一步提高了参数反演算法的性能。利用欧空局(ESA)发布的软件PolSARPro仿真验证了该文方法在植被参数反演方面具有更好的稳健性和估计精度。

极化干涉合成孔径雷达；植被参数反演；非平稳校正；映射空间均衡化；主成分分析

1 引言

极化干涉合成孔径雷达(Polarimetric Interference SAR, Interferometry, PolInSAR)因其对散射体材质、形状、方向和空间分布极为敏感，已越来越多的应用于地形测绘、海洋监测、农林业测绘、气象制图等领域，尤其在植被覆盖区地形干涉相位获取、植被参数估计(如森林高度、植被体衰减系数等)和森林分类与制图等应用领域表现出巨大的优势[1]。据统计，森林区域覆盖了全球大约30%的陆地面积，且平均树高达到20 m左右，植被参数反演对地球生物环境和碳循环平稳性的研究具有重要意义。目前利用极化干涉雷达数据进行植被参数反演的主要算法包括三阶段反演方法[24]-、基于样本相关矩阵的最大似然估计方法[5]、基于极化干涉互协方差模型的参数反演方法[6,7]和基于优化模型的地体散射分离方法[8]，其中以三阶段植被参数反演及其改进方法使用最为广泛，而最大似然方法和基于互协方差模型的植被高度反演结果均有所低估。此外，当前主流的这些算法均假设统计窗内观测样本具有独立同布特性，而实际上简单以空域平均代替集合平均无法补偿数据的幅相非平稳变化[9]。在经典的森林植被两层散射模型中，三阶段方法也未考虑观测信号在映射空间的非均匀分布密度对散布区域线性变化主导方向提取的影响。本文首先给出了观测样本数据幅度和相位非平稳变化自校正的补偿方法，详细分析了在统计模型非线性映射下，离散化的观测信号非均匀分布对散布区域线性变化主导方向估计的影响，并提出了基于映射空间均衡化(Mapping Space Regularization, MSR)的主成分分析(Principal Component Analysis, PCA)植被参数反演方法。实验结果表明，与传统主流算法相比本文方法具有更好的稳健性和更高的估计精度。

2 森林植被散射模型

森林植被散射一般被建模为由导向随机、均匀分布的植被体散射(Random Volume over Ground, RVoG)和地面散射构成的两层散射模型。基于这一假设，RVoG植被散射模型建立了不同极化状态下PolInSAR复相干系数()γω与地形干涉相位oφ、森林植被高度vh和衰减系数σ等参数的函数关系[2,10]。

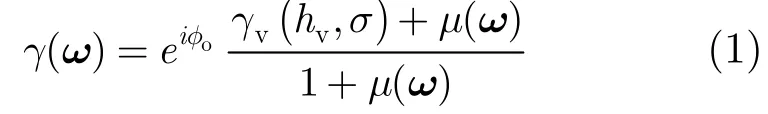
式中，i为虚数单位，oφ与地形高程有关，体散射去相干vγ随vh和σ变化。()μω表示地面散射与体散射幅度之比，与观测极化方式ω相关，()μ∈ω ()0,+∞。整理式(1)可以得到

在实际PolInSAR系统中，主辅雷达以不同的视角分别获取全极化散射向量k1, k2，则相应的极化相干矩阵可表示为

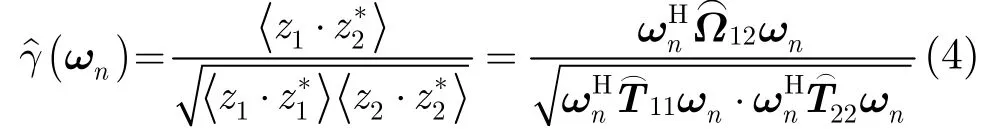
其中，zj=·kj(j =1,2)为对应于极化方式ωn的PolInSAR复图像数据，·表示集合平均。由此可见，PolInSAR观测信号是雷达观测极化方式ω向观测空间γ(ω)的投影，式(4)给出了这一映射法则。根据式(4)计算得到(ωn)，并结合模型式(1)即可实现地形干涉相位φo、森林植被高度hv和衰减系数σ等参数的估计。

在理想情况下，由式(1)给出的PolInSAR复相干系数在复平面单位圆内呈直线分布。然而，由于森林植被并不完全满足RVoG模型，而PolInSAR复相干系数的计算式(4)也存在一定的失配，这使得由观测样本计算得到的复相干系数不再满足直线模型，而是散布在复平面单位圆内近似椭圆的区域内。根据理论分析表明，该散布区域在复平面上是一个连续的凸集[11]。为了拟合得到能反应复相干系数整体线性变化规律的直线，常规的参数估计方法主要利用最小二乘线性拟合或对散布区域的长轴进行检测[12]等。例如文献[2]提出的经典三阶段反演算法，首先根据式(2)对观测得到的()在复平面上进行最小二乘拟合，然后利用先验信息确定拟合直线与单位圆的交点之一作为，并选取沿该直线方向与相距最远的(ωn)在直线上的投影作为，最后利用查表法(Look-Up Table, LUT)确定森林植被高度和衰减系数。此时，影响森林植被参数和地形干涉相位估计精度的关键在于PolInSAR复相干系数统计一致性样本的选取和散布区域线性变化主导方向的估计。实际上，观测样本数据幅度和相位的非平稳变化都会引起PolInSAR复相干系数的估计偏差，并且由雷达观测极化方式ω离散采样导致的复相干系数非均匀分布也会影响散布区域主导方向的估计性能。针对这些问题，本文在下文中将结合仿真实验给出详细的分析，提出了一种基于数据幅度和相位一致性校正的稳健植被参数反演方法。

3 基于映射空间均衡化的PCA植被参数反演算法

3.1 基于数据幅度和相位自校正的极化相干矩阵估计

PolInSAR复相干系数的估计好坏对参数反演结果有着直接的影响。对于复相干系数的估计，如式(4)所示，样本统计一致性越好，其统计结果就越能反映目标单元真实的散射特性。由于单基线PolInSAR仅能获取目标区域干涉信号的单次观测样本，通常式(4)利用空间平均来代替集合平均，并假定空间平均所用的样本是平稳且各态历经的[13]。然而，当地形有所起伏或地物散射特性变化较大时，观测信号的相位(受地形起伏影响)和幅度(受地物散射特性影响)难以满足各态历经特性，在估计复相干系数时估计结果会发生偏差，进而影响植被参数反演结果，因而必须对数据的幅度和相位非平稳性进行估计与补偿以保证样本的独立同分布特性。

PolInSAR系统以几乎相同的视角分别获取目标单元的全极化散射向量k1, k2，由式(3)可以得到反应目标单元散射特性的极化相干矩阵T。为使数据样本满足独立同分布特性，必须对各目标单元的极化相干矩阵T进行幅度和相位校正。通常假设统计窗内的像素单元为散射同质区，而统计窗内目标单元极化相干矩阵干涉通道的相位非平稳主要由地形干涉相位项eiφo引起，地物目标散射能量的差异也会引起幅度非平稳变化。因此，对于任意的目标单元(m,n)，经过幅度和相位校正的极化相干矩阵TAPC可表示为

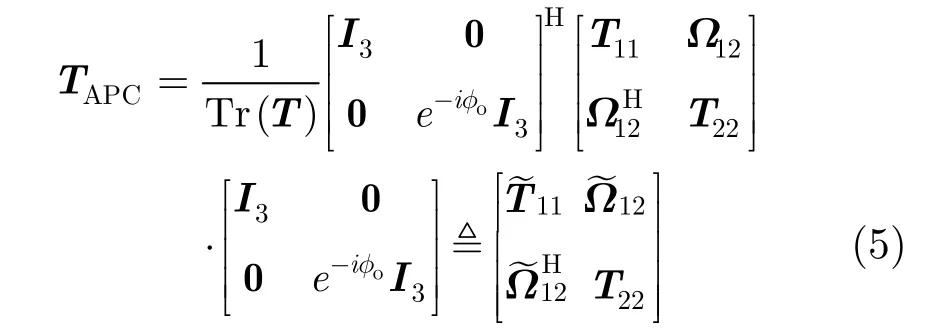
其中，()TrT表示由式(3)定义的极化相干矩阵T的迹，用于校正幅度非平稳对观测量的影响。采用式(5)对T进行幅度和相位校正后，即可利用式(4)计算PolInSAR复相干系数，其中

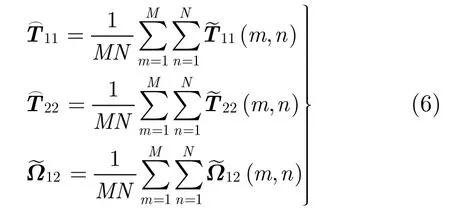
M, N为目标单元周围选取的统计窗尺寸。

针对以上方法的弊端，本文基于RVoG植被参数反演模型提出了地形干涉相位项的自适应迭代计算方法，(1)将地形干涉相位初始值设置为零；(2)利用式(5)对原始数据样本进行幅相非平稳校正，并通过式(6)和式(4)(计算极化干涉复相干系数；(3)采用本文提出的数据处理技术估计出各个像素对应的地形干涉相位项；(4)对观测场景的地形干涉相位复数据进行相位滤波[16]得到。重复以上步骤(2)～步骤(4)进行迭代计算可显著提高地形干涉相位的估计精度。本文采用欧空局(ESA)PolSARPro软件仿真了存在方位地形坡度(1.72°)和距离地形坡度(1.15°)的森林植被(平均高度10 m)极化干涉数据，并利用上述3种方法对地形干涉相位项进行估计，结果如图1所示。图1(a)为利用HH+VV极化通道干涉数据作为先验信息得到的地形干涉相位估计结果，图1(b)为最优相干分解方法估计结果，图1(c)为本文算法估计结果，图1(d)为仿真场景地形干涉相位(去平地相位后)的真实值。根据地形干涉相位可分别估算出方位地形坡度为1.718◦，距离地形坡度为1.147◦，与仿真参数相一致。图2为植被覆盖区地形干涉相位估计误差的统计直方图，可见本文算法能够很好地估计出地形干涉相位。仿真试验结果表明，在实际工程计算中一次迭代计算即可得到较为满意的估计结果。

3.2 映射空间均衡化处理

实际上，由于映射法则的非线性性质，散射机理空间Ω(雷达观测极化方式ω∈Ω)的均匀离散采样经过式(4)投影后，在观测空间γ(ω)呈现极强的非均匀分布。图3示意了PolInSAR复相干系数在复平面上的这种非均匀分布情形，近似椭圆的闭合曲线为当前像素对应的复相干系数散布区域包络(由大量观测所得)，其中虚直线表示利用这些非均匀散布点估计得到的直线模型，实直线为假设该包络内散布点均匀分布时估计得到的直线模型。由此可见，利用散布区域内均匀分布的散布点能更好地估计复相干系数线性变化的主导方向。观测信号(复相干系数)在观测空间的这种非均匀分布是由散射机理空间离散采样引起的，为了正确估计散布区域的线性变化主导方向，在参数反演过程中必须剔除观测信号非均匀分布对直线方向估计的影响。

图1 植被覆盖区地形干涉相位估计结果对比

由于观测信号的散布区域在复平面上是一个连续的凸集[11]，因此可以首先利用凸包络提取方法[17]在观测空间(即()γω域)得到该散布区域的包络，并对包络内区域进行均匀密度重采样，获取新的观测信号样本()γ~ω，实现映射空间()ω的均衡化处理。MSR处理可以表示为

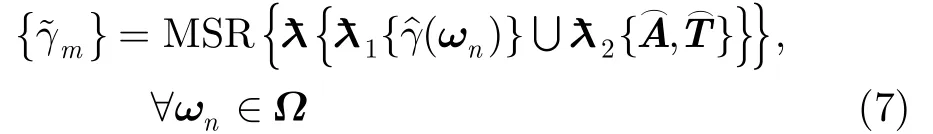
式中，ωn(n=1,2,…,N,∀ωn∈Ω)为任意选取的极化状态矢量，N 为选取的极化状态数量。=为基于文献[17]通过观测得到的复相干系数(ωn)计算的相干区域外包络集，2为基于文献[18]以和计算的相干区域外包络集。为子包络点集和的外包络总集合，作为相干区域真实外包络的鲁棒性估计结果。MSR{·}为映射空间均衡化算子，以实现对包络·所围合而成的复平面区域(即相干区域估计结果)进行离散均匀采样。经MSR处理后的相干区域可用复相干系数点集{}(m=1,2,…,M)进行表征，M为相应的采样点数。

3.3 基于主成分分析的主导方向稳健提取算法

常规采用的最小二乘方法容易受观测信号分布的影响，即使进行MSR处理也无法准确估计复相干系数线性变化的主导方向。如图4所示，观测信号已经过MSR处理，虚直线为利用总体最小二乘方法(Total Least Square, TLS)得到的主导方向直线模型，与之相比实直线所示的直线模型更符合观测信号散布区域的线性变化主导方向，而最小二乘的结果只是对应于观测信号散布点分布方差最小的情况。与最小二乘方法相比，长轴检测法[19](Detection with Longest Axis, DLA)不受观测信号非均匀散布的影响，对于图4所示的散布区域也能较好地估计出线性变化的主导方向。然而，当观测信号散布区域的分布形状有所变化时，如非椭圆凸集情况，DLA仍然无法准确估计出主导方向。如图5所示的4种情况，虚直线对应为DLA得到的主导方向直线模型，显然实直线所示的线性模型更能反映观测信号散布区域线性变化的主导方向。

一般地，观测信号在复平面上沿线性变化主导方向的分布方差必须足够大，而在与其正交的方向上分布方差应尽量小，以保证观测信号散布区域沿线性变化主导方向的线性度足够好。基于这一概念，本文引入PCA方法，通过主成分分析确定方差最大的综合变量为第1主成分，并以第1主成分方向作为观测信号线性变化的主导方向。根据PCA基本原理可知，第2主成分是第1主成分的最大不相关综合变量，可以理解为第2主成分方向与第1主成分方向正交，因此可以利用第1主成分与第2主成分贡献(对应于各自的分布方差)的比值作为观测信号数据沿第1主成分方向分布的线性度，即η= λ2/λ1。对线性度满足选定阈值α(例如取α=0.5)的像素，利用PCA方法估计其主导方向和线性变化模型。在上述示例的图3、图4和图5中，横、纵坐标分别表示复相干系数的实部、虚部，由图可见，与传统的三阶段反演算法和长轴检测方法相比，本文方法能够快速、稳健地对观测信号散布区域的线性变化主导方向进行准确估计，得到与PolInSAR复相干系数直线模型最优的匹配结果。

图2 地形干涉相位估计误差统计直方图

图3 观测信号非均匀分布 对主导方向估计的影响

图4 MSR后PCA(实线)与 LS(虚线)估计结果对比

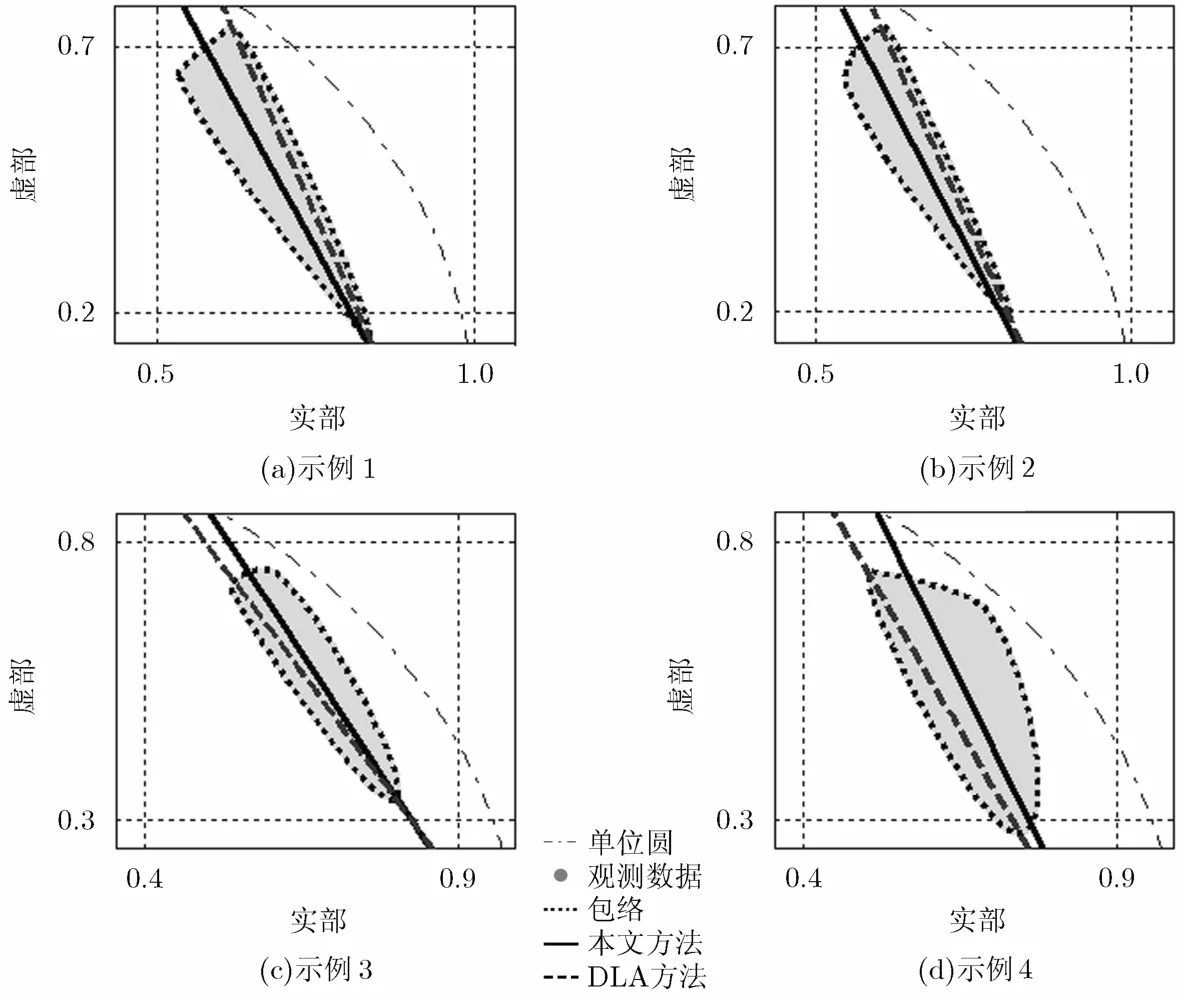
图5 DLA(虚线)与PCA(实线)估计结果对比

3.4 本文算法基本流程

基于MSR处理并利用PCA方法得到与直线模型式(2)最匹配的直线l后，我们可以利用先验信息完成森林植被的参数估计。由式(2)可知，地体散射比μ(ω)越大，则相应的γ(ω)越靠近地表散射中心对应的复相干系数γg，而离γg越远的γ(ω)其μ(ω)也越小。一般认为，HH, HH+VV和HH-VV3个极化通道的地表散射与体散射相比均占主导作用，这3个通道的地体散射幅度比μ(ω)均大于HV通道[2]。因此，这3个极化通道对应的复相干系数应位于γ(ωHV)和γg之间，据此可以确定直线l与复平面单位圆的交点之一作为γg的估计值。然而，由于数据统计误差或噪声的影响，实际计算的结果并非完全满足这一先验信息，如图6所示的实测数据各先验通道相干系数的相对位置关系。针对这一问题，本文分别将这几个极化通道的复相干系数(ωHV),(ωHV),(ωHH+VV)和ωHH-VV)向直线l作投影，并选取其中与(ωHV)投影间距最大的投影点作为近地点(即与(ωHV)相比，更靠近γg)，那么根据(ωHV)的投影和的相对位置关系就可以更为稳健地估计出地形干涉相位项。由于体散射中心复相干系数μ(ω)接近于零，因此本文选取{}中与投影间距最远的投影点作为体散射复相干系数估计值。最后，在去除地形干涉相位影响后，利用LUT方法可直接对植被参数进行准确估计。

综上所述，基于MSR处理的PCA植被参数反演及高精度地形获取算法的基本流程为：

(1)首先利用式(5)对去除平地相位的目标单元极化相干矩阵进行幅度和相位一致性校正，并利用式(6)统计计算各个目标单元的极化相干矩阵, ,。

(2)任意选取散射机理ωn(n=1,2,…,N,∀ωn∈Ω)，根据式(4)计算得到大量的观测信号样本{(ωn)}。

4 实验与结果分析

本节利用欧空局提供的L波段森林植被的PolInSAR仿真数据验证了幅相非平稳校正方法和基于MSR处理的PCA植被参数反演方法的性能。实验中利用欧空局研发的PolSARPro软件获取了均值高度分别为10 m, 16 m, 22 m的3组无地形起伏松树林、一组植被高度为10 m的无地形起伏灌木林和一组方位、距离地形坡度均为2°、高度为10 m的松树林极化干涉数据，主要的仿真参数如表1和表2所示。为了验证本文算法的有效性，本节通过表2中的几组仿真数据分别对各子处理环节依次进行验证。

仿真1 幅度非平稳校正方法性能验证。为了验证本文提出的幅度非平稳校正方法性能，本文采用3.4节中的算法流程，对表2中的第1组极化干涉数据进行处理。在对比试验中，数据处理的差异在于是否对数据进行幅度非平稳校正，图7为对比试验的参数反演结果统计直方图。受全极化干涉数据获取体制的限制，相干矩阵主要由空间统计窗内样本的平均计算得到，而统计窗内所选的样本并不完全满足统计一致性。如果所选样本的幅度非平稳影响没有去除，统计假设也将难以得到满足。因而，相干矩阵的估计误差将会累积到植被参数反演过程，严重降低参数估计精度，甚至引入较大误差。由图7可见，幅度非平稳性对参数估计结果有着显著影响，在数据预处理过程中必须予以去除。

表1 雷达几何仿真参数

表2 森林植被仿真参数

仿真2 相位非平稳校正方法性能验证。为了考察相位非平稳特性对参数估计的影响，本文在表2中第1组仿真数据的基础上引入了坡度为19.3◦的方位地形，相位非平稳特性影响对比试验中仍采用3.4节的算法流程，图8为植被高度参数反演结果统计直方图。由图8可见，植被参数估计结果的精度同样受相位非平稳性的影响，因此在数据预处理过程中也必须消除地形相位的影响。

仿真3 基于MSR处理的PCA方法性能验证。经数据预处理之后，主导方向的稳健提取成为植被参数估计的关键。为了验证本文提出的主导方向提取算法，本次仿真对比了基于MSR处理的PCA主导方向提取算法和经典TLS算法性能。为了有效评估本文算法性能，对比试验均采用3.4节的算法流程，不同之处在于步骤3和步骤4替换为TLS方法作为对比。试验采用表2中的第1组数据，图9所示为参数反演结果统计直方图对比。由图9可见，本文提出的算法能够更为精准有效地获取植被参数信息。

仿真4 算法总体性能验证。为了评估本文算法的整体性能，本节采用表2中的第5组数据与经典三阶段法进行了对比试验，图10为两种方法的参数反演结果统计直方图对比。由图10可见，本文算法在植被参数获取精度方面有明显的改善。为了便于算法性能对比，本节采用两种方法分别对表2中的5组试验数据进行处理，试验结果包括树高均值和均方误差(Mean Square Error, MSE)两个指标，如表3所示。

5 结束语

本文针对植被参数反演主流算法的缺陷，考虑观测样本数据的幅度、相位非平稳特性以及观测信号非均匀分布对其散布区域线性变化主导方向估计的影响，提出了基于幅相一致性校正的稳健PCA植被参数反演方法。该方法首先对原始观测数据统计样本进行幅度、相位非平稳自适应校正，然后通过映射空间均衡化处理消除观测信号非均匀分布对参数估计的影响，再采用主成分分析方法提取信号散布区域的线性变化主导方向，最后结合多通道先验信息利用LUT方法对植被参数进行快速准确的估计。基于幅相一致性校正的稳健PCA植被参数反演方法有效地消除了观测数据统计样本幅相非平稳特性的影响，解决了观测信号非均匀分布导致植被参数估计结果错误的问题。仿真数据处理结果表明，经过幅相一致性校正和映射空间均衡化处理后，植被参数估计的期望均值误差大大降低，能够更为稳健地对不同高度、不同种类的森林植被参数进行准确估计，保证了植被参数的估计精度，效果优于传统的植被参数反演算法。

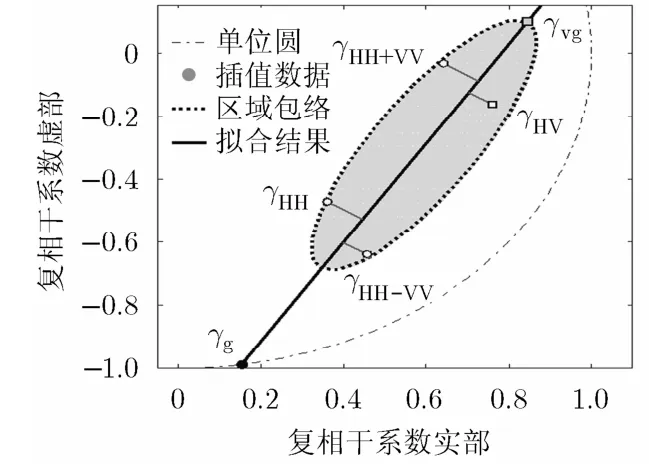
图6 基于MSR的PCA植被参数估计方法示意图

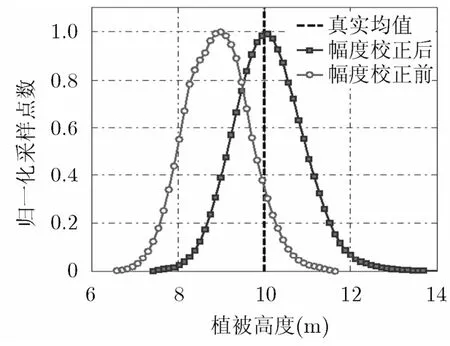
图7 幅度非平稳性对植 被高度参数估计的影响

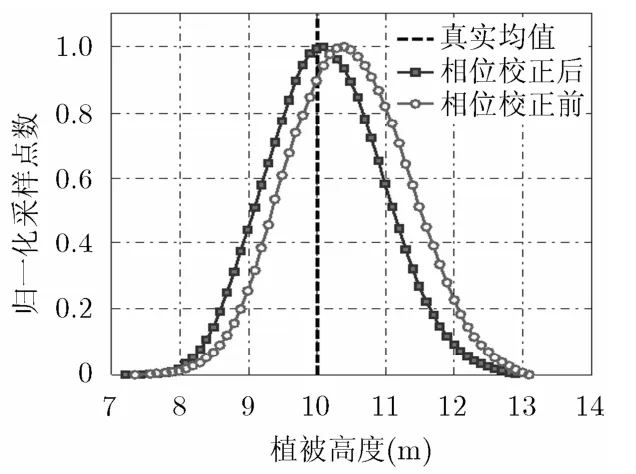
图8 相位非平稳性对植 被高度参数估计的影响

图9 基于MSR处理的PCA方法与常规TLS方法比较

图10 本文算法与经典三阶段法参数估计结果对比

表3 参数反演算法性能比较

[1] 钟雪莲, 向茂生, 郭华东, 等. 机载重轨干涉合成孔径雷达的发展[J]. 雷达学报, 2013, 2(3): 367-381. Zhong Xue-lian, Xiang Mao-sheng, Guo Hua-dong, et al.. Current development in airborne repeat-pass interferometric synthetic aperture radar[J]. Journal of Radars, 2013, 2(3): 367-381.

[2] Cloude S R and Papathanassiou K P. Three-stage inversion process for polarimetric SAR interferometry[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(3): 125-134.

[3] Lopez-Martinez C and Alonso-Gonzalez A. Assessment and estimation of the RVoG model in polarimetric SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, PP(99): 1-16.

[4] Li Zhen and Guo Ming. A new three-stage inversion procedure of forest height with the improved temporal decorrelation RVoG model[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 2012: 5141-5144.

[5] Tabb M, Flynn T, and Carande R. Full maximum likelihood inversion of PolInSAR scattering models[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 2004: 1232-1235.

[6] Nghia P M, Zou Bin, and Cheng Yan. Forest height estimation from PolInSAR image using adaptive decomposition method[C]. IEEE 11th International Conference on Signal Processing (ICSP), Beijing, China, 2012: 1830-1834.

[7] 李廷伟, 黄海风, 梁甸农, 等. 基于Freeman分解的植被参数反演新方法[J]. 电子与信息学报, 2011, 33(4): 781-786. Li Ting-wei, Huang Hai-feng, Liang Dian-nong, et al.. A novel vegetation parameters inversion method based on the Freeman decomposition[J]. Journal of Electronics & Information Technology, 2011, 33(4): 781-786.

[8] López-Martínez C and Papathanassiou K P. Cancellation of scattering mechanisms in PolInSAR: application to underlying topography estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 953-965.

[9] Refregier P, Roueff A, Arnaubec A, et al.. Invariant contrast parameters of PolInSAR homogenous RVoG model[J]. IEEE Geoscience and Remote Sensing Letters, 2014, PP(99): 1-4.

[10] Lu Hong-xi, Suo Zhi-yong, Guo Rui, et al.. S-RVoG model for forest parameters inversion over underlying topography[J]. Electronics Letters, 2013, 49(9): 618-619.

[11] Neumann M, Ferro-Famil L, and Reigber A. PolInSAR coherence set theory and application[C]. EUSAR 2006, Dresden, Germany, 2006: 453-456.

[12] Tabb M, Orrey J, Flynn T, et al.. Phase diversity: a decomposition for vegetation parameter estimation using polarimetric sar interferometry[C]. EUSAR 2002, Cologne, Germany, 2002: 721-724.

[13] Touzi R, Lopes A, Bruniquel J, et al.. Coherence estimation for SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(1): 135-149.

[14] Eineder M. Efficient simulation of SAR interferograms of large areas and of rugged terrain[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(6): 1415-1427.

[15] Papathanassiou K P and Cloude S R. Phase decomposition in polarimetric SAR interferometry[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seattle, WA, USA, 1998: 2184-2186.

[16] Suo Zhi-yong, Li Zhen-fang, and Bao Zheng. A new strategy to estimate local fringe frequencies for InSAR phase noise reduction[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(4): 771-775.

[17] Barber C B, Dobkin D P, and Huhdanpaa H. The quickhull algorithm for convex hulls[J]. ACM Transactions on Mathematical Software, 1996, 22(4): 469-483.

[18] Flynn T, Tabb M, and Carande R. Coherence region shape extraction for vegetation parameter estimation in polarimetric SAR interferometry[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, Canada, 2002: 2596-2598.

[19] 白璐, 曹芳, 洪文, 等. 相干区域长轴的快速估计方法及其应用[J]. 电子与信息学报, 2010, 32(3): 548-553. Bai Lu, Cao Fang, Hong Wen, et al.. Fast approach to estimate the longest axis in coherence region and its applications[J]. Journal of Electronics & Information Technology, 2010, 32(3): 548-553.

卢红喜： 男，1987年生，博士生，研究方向为极化InSAR信号处理、多基线InSAR信号处理、阵列优化设计与极化层析成像技术研究.

宋文青： 男，1988年生，博士生，研究方向为雷达目标识别、统计信号处理、统计机器学习等.

李 飞： 男，1984年生，博士生，研究方向为雷达成像和雷达目标特征提取.

刘宏伟： 男，1971年生，教授，博士生导师，研究方向为雷达系统、雷达信号处理、雷达自动目标识别等.

Forest Parameters Inversion Based on Nonstationarity Compensation and Mapping Space Regularization

Lu Hong-xi①Song Wen-qing①Li Fei①Wang Ying-hua①Liu Hong-wei①Bao Zheng①Huang Hai-feng②

①(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)
②(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 430074, China)

Forest parameters inversion is an important application of Polarimetric Interference Synthetic Aperture Radar (PolInSAR). The traditional inversion method does not take into account the amplitude and phase non-stationary of observation, and its non-uniform distribution effect on the estimation of the principal linear change direction. Aiming at these problems, an amplitude and phase calibration approach is proposed to compensate the polarization coherence matrix nonstationarity, to enhance the performance of complex coherences estimation. Moreover, this paper develops a Mapping Space Regularization (MSR) technology which promises to be able to eliminate the non-uniform distribution effect of sample coherences on the linear variation of complex coherences. Based on MSR, the Principal Component Analysis (PCA) is further introduced to the linear variation model extraction. Processing results of ESA PolSARpro simulated data verify the better robustness and estimation accuracy of the proposal in forest parameters inversion.

Polarimetric Interference SAR (PolInSAR); Forest parameters inversion; Signal nonstationarity compensation; Mapping Space Regularization (MSR); Principal Component Analysis (PCA)

TN957.51

A

1009-5896(2015)02-0283-08

10.11999/JEIT140261

2014-03-04收到，2014-06-20改回

国家自然科学基金(61271024, 61201292, 61201283)，新世纪优秀人才支持计划(NCET-09-0630)，全国优秀博士学位论文作者专项资金(FANEDD-201156)，国家部级基金，中国航天科技集团公司航天科技创新基金和中央高校基本科研业务费专项资助课题

*通信作者：卢红喜 xdkd@163.com