椭圆纳米薄膜的自旋波本征特性研究
2015-07-18张光富张学军邓杨保
张光富,张学军,邓杨保
椭圆纳米薄膜的自旋波本征特性研究
张光富,张学军,邓杨保
(湖南城市学院通信与电子工程学院,湖南益阳413000)
采用微磁学模拟方法研究了椭圆纳米薄膜的自旋波本征特性.获得了其自旋波频率谱和自旋波模式空间分布.由于空间受限,自旋波模式展示量子化和局域化特性.自旋波模式的空间对称性与激发场的对称性有关.磁薄膜的厚度能对自旋波模式特性进行调制.随着厚度的增加,边缘局域化模式和波矢方向沿着磁化方向的BA模式自旋波频率减小,而一致模式和波矢方向垂直于磁化方向的DE模式自旋波频率增大.
自旋波;微磁学;色散关系
磁纳米结构材料的动力学特性是自旋电子学的重要内容,与纳米磁存储器件、传感器件和逻辑器件等新型自旋电子器件的性能息息相关.充分理解磁纳米结构的动力学特性具有十分重要的理论和实际意义.近年来,磁纳米结构的一些动力学特性,如超快反磁化机制,微波发射,磁畴移动等,已得到了广泛研究和理解[1-3].研究显示这些磁动力学特性与纳米结构的本征自旋波模式存在密切的联系.F.Montoncello等人的研究[4-5]展示纳米结构的磁反转过程总是伴随着某种自旋波模式的软化(自旋波的频率为零),且软化的自旋波模式空间分布和对称性决定了磁反转过程中微磁结构的演变路径.另外,通过激发特定的自旋波模式可有效的减小反转场,也可获得希望的磁反转过程[6-7].因此,充分理解纳米磁体的本征自旋波特性对自旋电子器件的研发十分重要.但对于不同的应用对纳米磁体的自旋波本征的动力学特性有不同的要求,如何对纳米结构材料的自旋波本征动力学特性进行调控成为亟待解决的关键问题.
由于纳米磁体内边界受限,自旋波的量子化效应以及局域化效应等一些区别于块体材料的新特性已在多种不同形状和大小的磁体内得到了广泛认识[8-9].纳米磁体的自旋波频率依赖于磁体的内部场场分布和波矢量[10].由于边界受限,即使一致磁化的纳米磁体中的内部场也是强烈不一致.当自旋波在不一致内部场中繁衍时,自旋波波矢将随着内部场的变化而变化.在某一位置,这里的内部场是如此的大,以至于自旋波的波矢量变为虚数,自旋波无法继续向更大内部场位置传播而被反射.因此自旋波将被限制于磁体内自旋波波矢为实数的区域内,这一区域即为所谓的自旋波阱,即产生自旋波的局域化效应.当自旋波能繁衍于整个纳米磁体内时,形成量子化驻自旋波.由于空间受限,在纳米结构磁体内,非一致的退磁相互作用和复杂的边界条件,很难获得其自旋波色散关系的理论解析表达.但基于Landau–Lifshitz–Gilbert方程的微磁学模拟可完整描述受限磁体内磁矩随时间的动态变化过程,通过对时域信息的傅立叶分析可获得其自旋波特性而无需考虑复杂边界的具体表达.利用微磁学模拟方法去研究纳米结构磁体的动力学特性已在学术界得到了广泛认同,结果的正确性也得到实验和理论结果的证实.
边界受限体系的纳米磁体的形状、大小引起的形状各向异性对磁体的微磁结构分布、自旋波本征谱和自旋波模式的空间分布产生较大的影响[11].椭圆纳米膜作为磁纳米结构存储记录元的候选形状,其磁特性倍受学界关注.在本文中,将基于微磁学模拟方法对椭圆纳米点的自旋波本征特性,以及椭圆纳米膜的厚度对自旋波本征特性的调制特性进行系统的研究.
1 微磁学理论及模拟方法
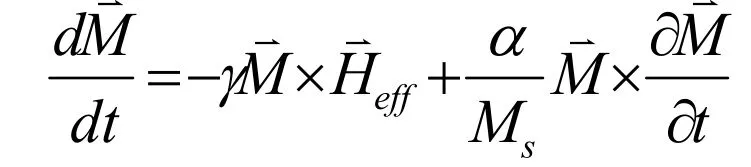
微磁学理论是一个连续介质理论,研究尺度介于磁畴宽度和晶格常数之间,从宏观角度讨论问题,以连续变化的磁化强度描述磁畴、磁矩的变化;是宏观磁性材料与微观局域磁化之间联系的纽带.微磁学理论认为除了在居里温度附近之外,在给定温度下,铁磁体的磁化强度大小保持不变,磁化矢量是时间和位置的连续函数,磁体系稳定的磁矩分布由磁体吉布斯自由能极小值确定,磁矩的动力学变化过程遵循Landau-Lifshitz-Gilbert动态方程[12].其中γ是旋磁比,M为磁体系磁化强度矢量,α为与材料相关的Gilbert阻尼常数.式中的Heff为磁体系的有效场,包括磁晶各向异性场,退磁场,交换场以及外磁场.有效场可表述为体系总自由能Etot的变分椭圆纳米膜的长半轴为200 nm,沿着z轴方向,短半轴为100 nm,沿着y轴方向,厚度t沿着x轴方向,坐标原点位于磁薄膜中心.利用微磁学模拟软件OOMMF[13]来研究厚度分别为1 nm-10 nm的10个椭圆纳米膜的自旋波动力学特性.模拟中网格剖分大小为2 nm×2 nm×t.磁纳米结构材料为磁信息存储中常用的软磁材料坡莫合金NiFe,磁参数为:饱和磁化强度|Ms|=0.86×106A/m;交换作用系数A=1.05 e×10-11 J/m;忽略磁各向异性.磁纳米膜初始平衡态是利用100 mT外磁场作用使磁体沿着z轴方向饱和磁化而获得.平衡态微磁结构展示除纳米点边缘磁矩存在少许偏离外磁场方向外,别的区域磁矩沿着外磁场方向一致排列.微磁学方法模拟计算分两步进行:第一步,磁矩线性进动.基于平衡态微磁结构,利用一外加脉冲激发磁场作用于磁矩,使其偏离平衡位置产生线性进动.脉冲激发磁场垂直于膜面(x轴方向),场强为0.5 mT,持续时间为200 ps,磁矩进动时阻尼因子为0.000 1,通过求解Landau–Lifshitz–Gilbert获得每一格点磁化矢量强度随时间的变化数据.为避免脉冲磁场对自旋波的影响,在脉冲磁场去除后磁体自由进动5 ns才开始记录磁矩随时间的变化.每隔5 ps记录一次数据,以确保可获得0-100 GHz范围内的自旋波,记录时间为20 ns.第二步,自旋波频率谱和自旋波本征模式的空间分布.基于模拟获得的各格点磁矩随时间的变化数据信息进行傅立叶变换,并对所有格点求平均获得自旋波频率谱.自旋波频率谱中的振荡峰对应不同的自旋波模式.利用各格点的傅立叶分析获得实部和虚部进行图像重构得到每一自旋波模式的空间分布.
2 结果与讨论
根据微磁学理论,纳米结构磁体内的磁矩进动依赖于力矩effvv´,因而外加脉冲激发磁场的对称性将对磁矩的进动方向产生影响.为了更全面理解纳米磁体内各种自旋波模式特性,除了采用均匀脉冲(Uniform)外,还利用关于z轴反对称脉冲(Odd z)和y轴反对称(Odd y)脉冲磁场激发自旋波,如图1中插图所示.这三种激发场作用于厚度为4 nm椭圆磁纳米膜时,激发出的自旋波频率谱展示于图1.图中的每一磁振荡峰对应着一种自旋波模式,其空间分布如图2中所示.这些自旋波模式根据文献[11]中分类方法,可以分为(i)边缘局域化模式自旋波(EM),自旋波的磁振荡处于磁体的末端边缘,而中央磁矩磁振荡的振幅为零.根据磁薄膜末端磁矩进动方向不同,存在两末端具有相同进动方向的对称模式(S-EM)和具有相反进动方向的反对称模式(S-EM).这两种模式一般具有简并的频率.(ii)n-BA模式驻自旋波,自旋波具有沿着外磁场方向的波矢,驻自旋波的节点线位于膜面内且垂直于外磁场方向,n为驻自旋波的节点数;类似于无限大磁体系中的BackWard模式自旋波.(iii)m-DE模式驻自旋波,自旋波的波矢垂直于个磁场方向,节点线平行于外磁场方向,m表示驻自旋波的节点数,类似于无限大磁薄膜的Damon-Eshbach模式自旋波,(iv)m-DE´n-BA混合模式驻自旋波,是m-DE模式和n-BA模式的混合模式.(v)F模式自旋波,磁体内磁矩都沿着同一方向进动,类似于椭球体中的铁磁共振Kitte一致振动模式[14].
均匀脉冲激发场作用时,自旋波频谱中最低频率振荡峰对应S-EM模式,由于边缘区域内强烈不一致的内部场分布产生的自旋波阱导致自旋波的局域化.频谱中最强的振荡峰对应的为磁矩一致进动的F模式自旋波.接下来的磁振荡峰对应的自旋波模式为量子数为偶数的BA模式、DE模式、以及混合模式量子化驻自旋波(如2-BA,4-BA, 2-DE,2-DE×2-BA等等).脉冲激发磁场为Odd-y时,由于磁薄膜左右两边磁矩进动方向不同,激发的自旋波模式与均匀激发场有很大不同.最低频率的振荡峰对应的局域化模式为AS-EM,而一致振荡F模式无法被激发,最强振荡峰为频率略小于F模式的1-BA量子化自旋波.频率更大的磁振荡峰所对应的自旋波为节点数为奇数的BA模式量子化自旋波(1-BA,3-BA,5-BA),以及偶节点数-DE×奇节点数-BA的混合模式自旋波(如2-DE ×1-BA,2-DE×3-BA,4-DE×3-BA),而DE模式未能被激发.脉冲激发磁场为Odd-z时,发磁场使磁纳米点面内上半部分和下半部分磁矩关于z轴反对称进动.因而更利于节点数为奇数的DE模式自旋波(如1-DE、3-DE和5-DE)以及奇节点数-DE ×偶节点数-BA的混合模式自旋波(如1-DE× 2-BA,1-DE×4-BA,3-DE×2-BA等)激发,而F模式,BA模式,AS-EM,S-EM模式却很难被激发.由于空间受限,椭圆纳米膜的自旋波模式展示量子化和局域化特性.自旋波模式的空间对称性依赖于激发场的对称性.
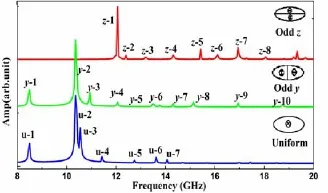
图1 具有不同对称性激发磁场作用下的,椭圆纳米膜的自旋波频率谱(图中的插图为激发磁场的对称性示意图)
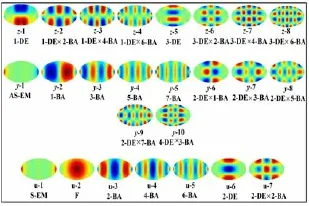
图2 椭圆纳米膜的自旋波模式空间分布
研究均匀脉冲作用下,磁层厚度对椭圆纳米膜自旋波特性的影响.图3展示了不同自旋波模式频率随着厚度的变化曲线,其中实心符号线为模拟计算得到的结果.图中展示了厚度对不同自旋波模式频率具有不同的调制作用.S-EM模式和BA模式自旋波频率随着磁纳米点厚度的增大而减小,而且,厚度对边缘局域化模式的影响明显大于对BA模式的影响.F模式和DE模式自旋波频率却随着厚度的增大而增大,但F模式受到厚度的影响较小,厚度从1 nm变化到10 nm过程中,F模式自旋波的频率变化仅为1.2GHz.2-DEl2-BA混合模式自旋波频率随着厚度的增大也增大.
磁纳米膜厚度的增大,增大了垂直于膜面的退磁场,减小了沿着磁化方向的退磁场.退磁场实质是远程相互作用,是一耦极作用场,其大小依赖于磁矩相对位置.因此厚度的变化,改变了静态退磁场分布同时,磁矩的磁振荡过程导致的动态耦极相互作用也将受到调制.因此,不同的自旋波模式受到磁薄膜厚度的影响也不相同.为了更深入的理解磁纳米膜厚度对自旋波的影响,基于方程(2)所示的均匀磁化矩形纳米薄膜近似色散关系[10]对椭圆纳米膜的本征自旋波特性进行了分析研究.
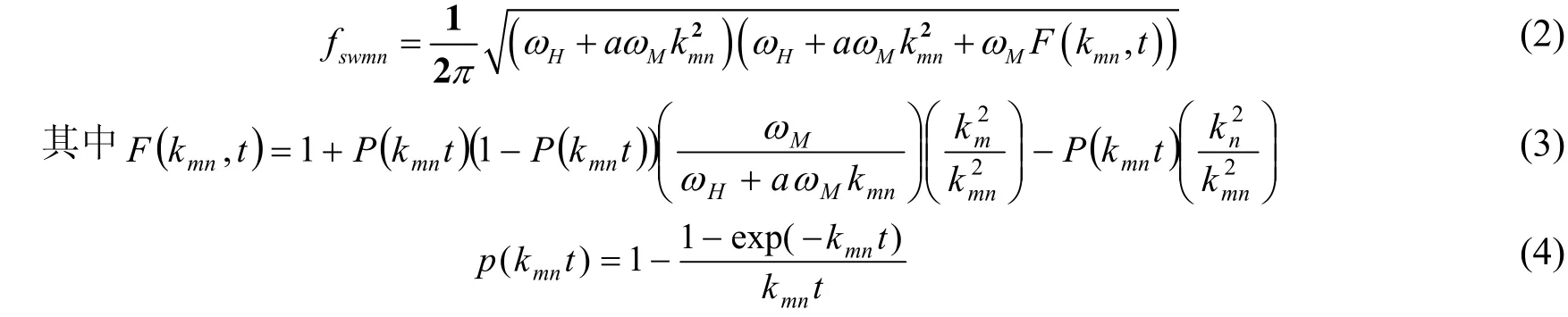
色散方程(2)中wH=gHint描述内部场分布对自旋波频率的影响,Hint为内部场;awMkm2n描述动态交换相互作用,wH=gMs和a=2Aex/(μ 0Ms);F(kmn,t )描述动态耦极相互作用,(3)式为其具体表达式;t为磁性层厚度.由于磁薄膜厚度远小于磁层膜面宽度和长度,可认为磁层厚度方向为一致振荡,kx=0.波矢量k2mn=kmy2+knz2描述膜面内二维波矢,kmy和knz分别为垂直和平行于静态磁矩方向波矢,m、n分别为垂直(平行)磁化方向波矢量的节点数.

图3 自旋波模式频率随着椭圆磁纳米点厚度的变化曲线
图中实心符号实线为模拟计算结果,空心符号虚线为理论分析计算结果,(a)黑色,红色,蓝色曲线分别对应S-EM,2-BA和4-BA模式自旋波,(b)黑色,蓝色和粉红色曲线分别对应F,2-DE和4-DE模式自旋波,(c)红色为2-DEl2-BA混合模式自旋波.
图4(a)中展示了厚度为4 nm椭圆薄膜的内部场分布,垂直于磁化方向(y轴方向)内部场几乎一致,但沿着磁化方向(z轴方向)内部场强烈不一致.在图4(b)中不同厚度纳米薄膜沿着z轴方向内部场分布展示随着磁薄膜厚度的增大内部场减小,内部场强烈不一致的边缘区域向磁体中央扩展.在平行磁化方向,内部场强烈不一致,磁矩必须改变自已的波矢量来获得相同的自旋波振荡频率,因此,沿着z轴方向波矢量随着位置变化.在平行于磁化方向,波矢量knz可近似的表示为kn=(n+1)p/Dln,Dln为自旋波模式的局域化长度.局域化长度Dln可根据文献[15]方法获得.对于垂直于磁化方向波矢量kmy,考虑耦极边界条件[16],km=mπ/wn,其中wn为磁体有效宽度.wn= wd(p)/(d(p)–-2),其中d(p)=2π/p[1+2ln(1/p)];p=t/w,w为磁体的宽度.由于内部场的不一致分布,基于微磁学模拟获得的内部场分布,每一种自旋波模式的内部场可计算自旋波局域区域内的平均内部场来近似表示Hint.因而,将波矢量km和kn以及Hint代入色散方程(2)可计算获得每种自旋波模式的频率.理论计算结果展示于图3中的点-虚张所示,可以看出理论结果与模拟结果符合的很好,利用近似色散关系可较好的解释磁层厚度对自旋波频率的影响.另一方面,理论计算过程中也展示了内部场,动态交换相互作用以及耦极相互作用对不同的自旋波模式的贡献,更利于理解厚度对不同自旋波模式的调制特性.
对于边缘局域化模式,磁振荡处于磁矩非一致分布的磁体边缘窄区域内.随着厚度增大,内部场减小.由于自旋波频率减小,局域化模式的局域区域减小,因此,自旋波的波矢量增大.动态交换相互作用随着磁层厚度的增大而增大,但其对频率的贡献与磁层厚度增大导致频率减小的贡献相当.引起自旋波频率减小的主要因素是由于z方向波矢量引起动态耦极相互作用导致自旋波频率随着厚度的增大而减小.就量子化驻自旋波而言,磁振荡局域于磁体中央磁矩一致分布区域,交换相互作用对自旋波频率的影响较小几乎可以忽略.就2-BA模式自旋波而言,计算展示自旋波的磁振荡区域随着磁场厚度的增大几乎不变.内部场以及沿着z方向的动态耦极相互作用随着厚度的增大而导致自旋波的频率减小.DE模式自旋波,磁振荡区域随着厚度的增大而减小.内部场和沿着z轴方向的动态耦极相互作用导致自旋波频率减小,但相对于y方向的动态耦极相互作用对频率的贡献小的多.y方向的动态耦极相互作用对频率的贡献是导致DE模式自旋波频率随着厚度增大的主要因素.F模式的磁振荡区域随着磁层厚度的增大也几乎不变,自旋波频率随着厚度的变化主要是由于内部场与y方向的动态耦极相互作用竞争的结果.混合模式驻自旋波m-DEln-BA,平均波矢量依赖于量子数m和n,因此对于不同的自旋波模式波矢量有较大的差异.对于2-DEl2-BA混合模式自旋波随着厚度的增大其局域区域减小,类似于DE模式,y方向的动态耦极相互作用对频率的贡献是使自旋波频率增大的主要因素.码.(b)具有不同厚度的磁纳米点内,y=0处内部场Hi(z)在z轴方向的分布曲线.

图4 (a)微磁学模拟获得厚度为4nm椭圆磁纳米点平衡态时内部场分布,图上端插图为标注内部场大小的颜色条
3 结论
基于微磁学模拟方法研究了椭圆纳米结构磁薄膜的自旋波本征模式特性.获得其自旋波频率谱以及自旋波模式空间分布.在磁体边缘,由于内部场强烈不一致形成自旋波阱而产生自旋波局域化;边界受限也导致了磁体形成量子化驻自旋波.磁纳米结构薄膜的厚度可以对自旋波模式频率进行调制,边缘模式和BA模式频率随着厚度的增大而减小,而F模式和DE模式频率随着厚度的增大而增大.基于均匀磁矩形纳米膜的近似色散关系对椭圆纳米膜的自旋波频率进行理论计算,结果与模拟结果符合得较好.并对不同的自旋波模式随磁层厚度变化规律进行了理论解释.
[1]R.Rückriem,T.Schrefl,and M.Albrecht,Ultra-fast magnetic vortex core reversal by a local field pulse[J].Appl.Phys.Lett, 2014,104(5):052414-1-4.
[2]P.Tanmoy,R.Urmimala,T.Maxim,et al.Micromagnetic simulationsofspin-wavenormalmodesandthe spin-transfer-torquedrivenmagnetizationdynamicsofa ferromagnetic cross[J].J.Appl.Phys,2014,115(17):17D123-1-3
[3]Wang X.G,Guo G.H,Nie Y.Z,et al.Microwave-assisted domain-wallmotioninducedbyalternatingspin-polarized current[J],Phys Rev B,2014,89(14):144418-1-6.
[4]F.Montoncello,L.Giovannini,and F.Nizzoli.Soft spin modes and magnetic transitions in trilayered nanodisks in the vortex state[J].J.Appl.Phys,2009,105(07):07E304-1-3.
[5]F.Montoncello,L.Giovannini,et al.Dynamic origin of first and second order phase transitions in magnetization reversal of elliptical nanodots[J].Phys.Rev.B,2008,77(21):214402-1-6.
[6]M.Kammerer,M.Weigand,M.Curcic,et al.Magnetic vortex core reversal by excitation of spin waves[J].Nat Commun,2011, 2:279-1-6.
[7]Seki Takeshi,Utsumiya Kazutoshi,Nozaki Yukio,et al.Spin wave-assisted reduction in switching field of highly coercive iron-platinum magnets[J].Nat Commun,2013,4:1726-1-8.
[8]S.K.Kim,Micromagnetic computer simulations of spin waves in nanometre-scale patterned magnetic elements[J],J.Phys.D:Appl. Phys,2010,43(26):264004-1-26.
[9]G.Gubbiotti,M.Conti,G.Carlotti,et al,Magnetic field dependence of quantized and localized spin wave modes in thin rectangular magnetic dots[J],J.Phys.:Condens.Matter,2004, 16(77):7709-1-13.
[10]C.Bayer,J.Jorzick,B.Hillebrands,et al,Spin-wave excitations in finite rectangular elements of Ni80Fe20[J],Phys.Rev.B,2005, 72(6),064427-1-12.
[11]G.Gubbiotti,G.Carlotti,T.Okuno,et al,Spin dynamics in thin nanometric elliptical Permalloy dots:A Brillouin light scattering investigation as a function of dot eccentricity[J],Phys.Rev.B, 2005,72(18),184419-1-8.
[12]T.L.Gilbert.A Lagrangian Formulation of the Gyromagnetic EquationofMagnetizationField[J].Phys.Rev.1955, 100(3):1243-1246.
[13]M.J.Donahue and D.G.Porter,OOMMF User’s Guide, Version 1.2a3,2002,http://math.nist.gov/oommf/.
[14]C.Herring and C.Kittel,On the Theory of Spin Waves in Ferromagnetic Media[J].Phys.Rev,1951,81(2):869-871.
[15]S.Neusser,B.Botters,andD.Grundler,Localization, confinement,and field-controlled propagation of spin waves in Ni80Fe20antidotlattices[J],Phys.Rev.B,2008,78(5): 054406-1-10.
[16]K.Yu.Guslienko and A.N.Slavin,Boundary conditions for magnetization in magnetic nanoelements[J],Phys.Rev.B,2005, 72(1),014463-1-5.
(责任编校:陈智全)
Study of the Spin-wave Eigenmodes in thin Nanometric Elliptical Magnetic Films
ZHANG Guang-Fu,ZHANG Xue-Jun,DENG Yang-Bao
(College of Communication and Electronic Engineering,Hunan City University,Yiyang 413000,China)
Thespin-wave eigenmodes in thin nanometric elliptical magnetic films are investigated using micromagnetic simulations.The oscillation spectrum and spatial distributions of Spin-wave eigenmodes are obtained.The spin-wave modes reveal quantized and localized features due to the geometrical confinement. The symmetry of the spin-wave modes is determined by the symmetry of the exciting fields.It is found that the properties of spin-wave eigenmodes can be tuned by changing the thickness of the element.For the EM and the BA modes,the frequency decreases with the thickness,while for the F and DE modes,its frequency increase with the increase of thickness.
spin-wave;micromagnetic;dispersion relation
O482.5
A
10.3969/j.issn.1672-7304.2015.01.014
1672–7304(2015)01–0054–05
2014-12-19
湖南省自然科学基金青年资助项目(14JJ6043);益阳市科技计划资助项目(2014JZ54)
张光富(1981-),湖南邵阳人,讲师,主要从事纳米结构材料特性研究.
