模拟填筑层数及水位对坝体变形及稳定性的影响
2015-07-18周爱红何国峰
周爱红,袁 颖,何国峰
(石家庄经济学院 勘查技术与工程学院,石家庄 050031)
模拟填筑层数及水位对坝体变形及稳定性的影响
周爱红,袁 颖,何国峰
(石家庄经济学院 勘查技术与工程学院,石家庄 050031)
坝体的变形及稳定性计算分析中,合理地选择模拟填筑层数并考察水位对坝体变形及稳定性的影响是十分必要的。首先以变形和稳定性系数作为评价指标,利用强度折减法计算坝坡的稳定性系数,基于FLAC3D建立坝体的分层填筑三维数值模型,对施工填筑期的数值模拟填筑层数的选取标准进行了研究。其次,在合理的模拟填筑层条件下,研究了不同蓄水位对坝体的变形和稳定性的影响。结果表明:坝体的变形以沉降为主,模拟计算的坝体沉降与填筑层数关系很大。相对坝体沉降来说,水平位移和稳定性系数对填筑层数的敏感性小,应以满足坝体沉降的精度标准选择模拟填筑层数,建议模拟填筑层数不少于10层,坝越高,选取的模拟填筑层数宜越多;坝体的水平位移对库水位位置较敏感,沉降和稳定性系数对库水位位置敏感性小。这些结果在坝体变形和稳定性研究中对确定合适的填筑层数和考虑库水位的影响具有指导意义。
分层填筑;填筑层数;坝体变形;沉降;稳定性;稳定性系数;数值模拟
1 研究背景
土石坝的数值计算,应按照施工填筑和蓄水过程,模拟坝体分期和加载的条件[1]。土石坝是分层填筑的,每层填筑厚度较小,一般都要小于1 m。在数值模拟中,通常取定填筑层数,把几个实际施工层作为一个填筑层,采用分层逐级加载的方法模拟坝体逐级填筑的施工过程[2-3]。殷宗泽等[4]最先对坝高为57 m的花凉亭黏土心墙砂壳坝进行应力应变分析,坝体模拟填筑层数取用5层。沈珠江等[5]对坝高48.6 m的横山土石坝进行应力应变分析,坝体模拟填筑层数取用12层。杨荣等[6]对坝高186 m的瀑布沟堆石坝进行应力应变分析,坝体模拟填筑层数取用6层。钱亚俊等[7]对坝高为701.6 m的新疆水利枢纽砂砾石黏土心墙坝进行了应力应变分析,坝体模拟填筑层数取用17层。邹波忠[8]对坝高为56 m的任宗海堆石坝的变形及坝坡的稳定性进行了分析,坝体模拟填筑层数取用11层。从这些文献可以看出,对不同坝高的坝体模拟填筑层数的选取,并没有统一的标准。唐岷等[9]以高300 m的土石坝为例,研究了分层模拟的填筑层数对沉降量的影响,得出模拟300 m级的土石坝沉降量,填筑层数应至少达到25~30层。刘喜珠等[10]以高为100 m的堆石坝为例,研究了填筑层数对坝体变形的影响,得出对于百米级高面板堆石坝,建议模拟分层厚度按坝高的0.1选取。谢江红等[11]对坝高为136 m的堆石坝进行了填筑10层和填筑20层的数值模拟,得出模拟的填筑层数对坝体的计算沉降量有重要影响。然而,这些研究着重于模拟填筑层数对坝体变形的影响,但是对坝坡稳定性影响如何,也值得深入研究。本文以变形和稳定性系数作为评价指标,对数值模拟填筑层数的选取标准进行了研究,并在合理的模拟填筑层模型基础上,研究了不同蓄水位对坝体的变形和稳定性的影响。
2 计算模型
本文基于FLAC3D软件[12]编制相应的计算程序对以上2个问题进行研究。以一坝高为10 m的小型黏土坝为例进行模拟填筑层数及水位对坝体变形及稳定性的影响研究。坝顶宽6 m,上下游坝坡为1∶1.2,坝横截面沿坝轴线方向不变。假定土坝坐落在完整性好的坚硬基岩上,坝体分10层施工,变形稳定后再填筑下一层,施工质量好,水库蓄水后很快达到预定水位,可视为坐落在不透水地基上的均质土坝。为了获得合适的模拟填筑层数,文中选取了2种工况。工况1取填筑层数为5层,每层填筑2 m;工况2与实际施工层一致,填筑层数为10层,每层填筑1 m。在工况2的基础上,进一步研究半库水位(水位在坝底以上半坝高位置)和满库水位对坝体的变形和稳定性的影响。
坝体材料的本构模型采用弹塑性本构模型,破坏准则采用摩尔-库仑屈服准则。结合相关规范和工程地质手册,坝体力学参数取为:体积模量7.6 MPa,剪切模量3.0 MPa,黏聚力20 kPa,摩擦角20°,密度1 800 kg/m3。
采用FLAC3D的Brick单元,进行坝宽范围内坝体的剖分,其他范围内坝体采用Uwedge单元进行剖分,建立几何模型,共850个单元,1 122个节点,然后将材料属性和边界条件赋给几何模型,得到物理模型,网格剖分图见图1。

图1 网格剖分
3 施工填筑期坝体的变形及稳定性分析
坝横截面、位移边界条件关于坝轴线对称,坝体成层水平填筑,受力条件也关于坝轴线对称,因此坝体变形和稳定性也关于坝轴线对称,相应计算结果提取坝体的一半进行分析。在施工填筑过程中,通常会对沉降和水平位移进行监测,并对这些资料及时进行分析,判断模拟计算结果的正确性和合理性。因此,文中相应给出了沉降、水平位移等值线图及坝轴线上沉降分布曲线及层面极值沉降分布曲线。
3.1 施工填筑期坝体的变形
工况1和工况2的坝体沉降等值线图见图2,水平位移等值线图见图3,坝轴线上工况1和工况2的沉降分布曲线和层面沉降极值分布曲线见图4。
从图2可以看出:沉降极大值出现在坝轴线上。对于工况1而言,当模拟层厚为2 m时,沉降极大值出现在坝体中上部,且明显地分为2个区域。一个极大值区域中心位于6.1 m左右,另一极大值区域中心位于7.9 m左右。对于工况2而言,当模拟层厚为1 m时,最大沉降值出现在坝体中部靠上5.6 m左

图2 不同工况下坝体沉降等值线

图3 不同工况下坝体水平位移等值线
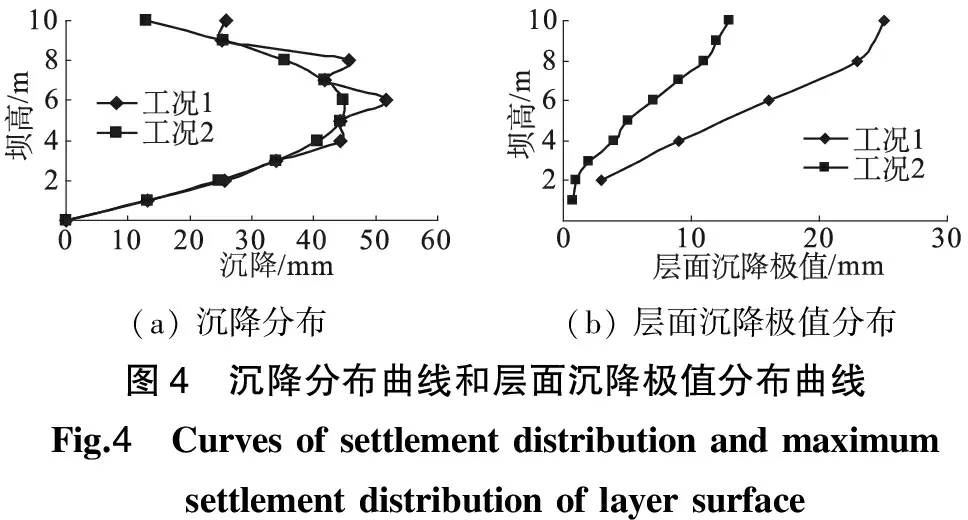
(a)沉降分布(b)层面沉降极值分布图4 沉降分布曲线和层面沉降极值分布曲线Fig.4 Curvesofsettlementdistributionandmaximumsettlementdistributionoflayersurface
右的位置,最大值附近等值线区域比较饱满,沉降量小。
从图3可以看出:工况1和工况2的水平位移分布规律相似,最大值出现位置相近,都出现在坝高的下部,约3.5 m附近,最大值也相近,约为15 mm。说明水平位移对填筑层数的敏感性远远小于沉降对填筑层数的敏感性。
工况2的水平位移最大值,约是相应最大沉降的1/3,可见均质土坝的变形以沉降为主。
从图4(a)可以看出:工况1的沉降分布曲线呈不规则的波浪型,不符合实际施工坝体沉降特点;工况2的沉降分布曲线近似呈关于半坝高对称的光滑曲线(除去1 m高度以下沉降),与实际施工坝体变形特点相符。在1/3坝高以下,工况1和工况2的沉降分布曲线基本重合,而在1/3坝高以上,工况2的沉降分布曲线经过工况1的沉降分布曲线的波谷点,填筑层层面沉降偏大较多,误差较大。
从图4(b)可以看出:2种工况的层面沉降极值分布曲线变化趋势相似,除了后面填筑的1/5坝高之外,前面填筑的各层层面沉降极值分布曲线近似呈线性变化,工况1的层面沉降极值分布曲线近似以0.35%的变化率线性增加,工况2的层面沉降极值分布曲线近似以0.17%的变化率线性增加;工况1的层面沉降极值远大于相应位置工况2的层面沉降极值。
如果模拟计算的沉降计算结果远大于监测的沉降值,则要考虑选取的模拟填筑层数是否太少。若以沉降作为确定模拟填筑层数的指标,对不同坝高的均质土坝,如何选取模拟填筑层数?经过大量分析计算,发现不同坝高的沉降变化规律一致,这里给出20 m土坝模拟填筑层数分别为10,15,20层的沉降分布曲线,见图5。

图5 不同填筑层数坝体沉降分布曲线
和前面一样,仍假设每层填筑1m,填筑层数为20层的情况,与实际施工一样。从图5可以看出:填筑10层和填筑15层的沉降,在1/3坝高以上计算的沉降误差较大,尤其是靠近坝顶附近区域,计算的沉降误差更大,填筑10层的沉降比填筑15层的沉降误差更大。对比图4中a图,可看出同样是填筑10层,但20 m的坝在1/3坝高以上沉降误差要比10 m的坝在1/3坝高以上沉降误差大较多。
综合以上分析,建议对不同坝高的均质土坝,选择模拟填筑层数时,应综合考虑坝的高度、工程精度要求和计算效率,选择合适的模拟填筑层数。可分区域选择填筑层数,从坝底到1/3坝高左右为第1区域,靠近坝顶范围为第3区域,其它为第2区域。第1区域填筑层稀疏,第3区域填筑层密,第2区域填筑层居中,即从坝底到坝顶按照疏-中-密的原则选择填筑层数。一般来说,坝越高,选取的模拟填筑层数宜越多。建议模拟填筑层数不少于10层,根据沉降分布曲线近似呈关于半坝高对称的光滑二次抛物线的特点,进行沉降修正[4,13]。
3.2 坝体的稳定性
滑动面位置和形态,可通过破坏状态的位移等值线图来表征。工况1和工况2的坝体稳定性系数都为1.55,整体上坝体内的应力场受填筑层数的影响较小,使得坝体的稳定性受填筑层数的影响较小。限于篇幅,这里只给出工况2的破坏状态的位移等值线图,见图6。从图6可明显看出均质压实黏土坝的滑动面形状为圆弧形。

图6 工况2的破坏状态的位移等值线
4 水库蓄水后坝体的变形及稳定性研究
在合理模拟填筑层条件下,下文以工况2为例,进一步研究半库水位和满库水位对坝体变形和稳定性的影响。
4.1 水库蓄水后坝体的变形
半库水位和满库水位时沉降等值线图见图7,水平变形等值线图见图8。由图7、图8可见,随着库水位的抬高,沉降最大值出现位置逐渐向迎水面移动,但数值变化很小。水平位移极大值出现位置逐渐抬高,并向迎水面移动,其大小随着水位的抬高而增加,相对沉降来说,水平位移对库水位的位置更敏感。
4.2 水库蓄水后坝体的稳定性

图7 半库及满库水位时坝体的沉降等值线

图8 半库及满库水位时坝体的水平位移等值线
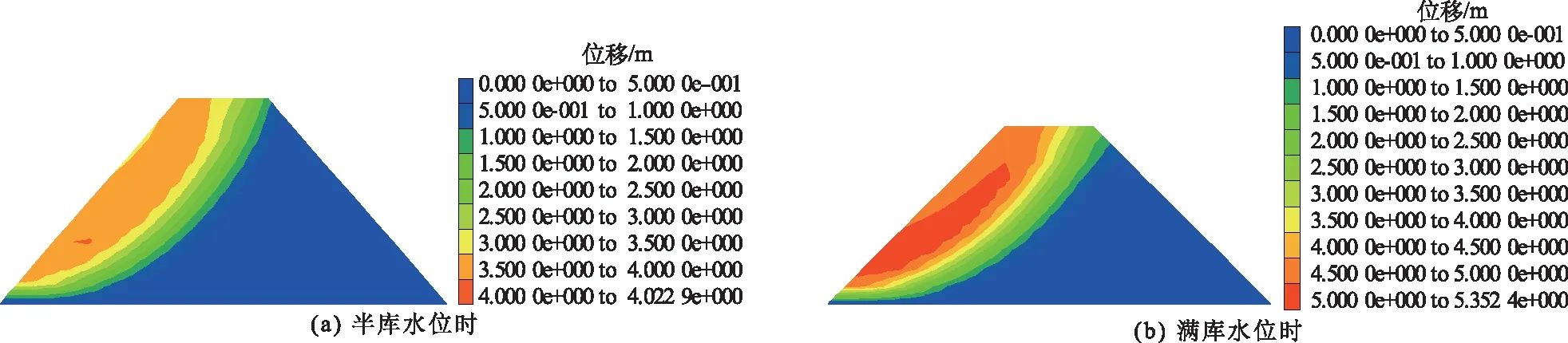
图9 半库及满库水位时破坏状态的位移等值线
半库水位和满库水位时坝坡的稳定性系数相同,都为1.55,破坏状态时的位移等值线图见图9。由图9可见,满库时的滑坡量要比半库时的滑坡量大较多。
5 结 论
通过研究模拟填筑层数及水位对坝体变形及稳定性的影响,得出如下结论:
(1) 模拟填筑层数对水平位移及坝坡的稳定性影响较小,应以满足坝体沉降的精度标准选择模拟填筑层数。坝越高,选择的模拟填筑层数宜越多。建议模拟填筑层数不少于10层,可从坝底到坝顶分3个区域,按照疏—中—密的原则选择填筑层数。
(2) 相较沉降和坝坡稳定性来说,水平位移对水位更敏感。不透水地基上坝体不透水时,水位越高,并不一定坝坡稳定性系数越低,稳定性越差,从另一侧面也反映了坝体的透水性是降低坝坡稳定性的原因。考虑坝体透水性的坝坡变形及稳定性研究将在后续工作中开展。
[1] SL274—2001,碾压式土石坝设计规范[S]. 北京:中国水利水电出版社, 2002. (SL274—2001, Design Code for Rolled Earth-Rock Fill Dams [S]. Beijing: China Water Power Press, 2002. (in Chinese))
[2] NAYLOR D J. Finite Element Methods for Fills and Embankment Dams[M].Advances in Rockfill Structures,Dordrecht:Kluwer Academic, 1991:291-340
[3] ZOMORODIAN SMA, SAHEBZADEH K, HAGHIGHI AT. Effect of Number of Layers on Incremental Construction Analysis of Earth and Rockfill Dam[M]∥Dams and Reservoirs, Societies and Environment in the 21st Century, London: Taylor& Francis, 2006:825-830.
[4] 殷宗泽, 曾益山. 花凉亭土坝应力应变分析[J]. 岩土工程学报, 1982, 4(4): 128-145.(YIN Zong-ze, ZENG Yi-shan. Nonlinear Stress-Strain Analysis for Hualiangting Earth Dam [J]. Chinese Journal of Geotechnical Engineering, 1982, 4(4):128-145. (in Chinese))
[5] 沈珠江, 王剑平. 横山水库土石坝有效应力应变分析[J]. 水利学报, 1990, (4): 59-65.(SHEN Zhu-jiang, WANG Jian-ping. Effective Stress and Strain Analysis in Earth Dam of Hengshan Reservoir [J]. Journal of Hydraulic Engineering, 1990, (4): 59-65.(in Chinese))
[6] 杨 荣. 瀑布沟高土石坝三维非线性分析[J]. 应用基础与工程学学报, 1995, 3(3): 260-267.(YANG Rong. The 3-D Nonlinear Stress-Strain Analysis of Pubugou High Rockfill Dam [J]. Journal of Basic Science and Engineering, 1995, 3(3): 260-267.(in Chinese))
[7] 钱亚俊, 陈生水. 心墙坝应力变形数值模拟结果验证[J]. 水利水运工程学报, 2005,(4): 11-18.(QIAN Ya-jun, CHEN Sheng-shui. Verification of Numerical Simulation Results of Stress and Deformation of Core-Wall Dams [J]. Hydro-science and Engineering, 2005, (4): 11-18.(in Chinese))
[8] 邹波忠. 仁宗海堆石坝在填筑过程中的变形分析与坝坡稳定性研究[D]. 成都: 成都理工大学, 2009. (ZOU Bo-zhong. Analysis of Deformation in Embankment Process and Research on the Stability of Dam-Slope of Renzonghai Rock-Fill Dam [D]. Chengdu: Chengdu University of Technology, 2009. (in Chinese))
[9] 唐 岷, 陈 群. 分层填筑模拟的层数对300 m级高土石坝沉降量的影响[J]. 水电站设计, 2008, 24(4): 15-19. (TANG Min, CHEN Qun. Influence of Simulated Fill Layer Number on Settlement of 300m High Embankment Dams [J]. Design of Hydroelectric Power Station, 2008, 24(4): 15-19. (in Chinese))
[10]刘喜珠, 练继建, 何龙军, 等. 面板堆石坝填筑仿真及堆石料参数影响研究[J]. 水利水电技术, 2010, 41(4): 32-35. (LIU Xi-zhu, LIAN Ji-jian, HE Long-jun,etal. Study on Simulation of Filling Construction and Impact from Parameter of Rockfill Material for Concrete Face Rockfill Dam [J]. Water Resources and Hydropower Engineering, 2010, 41(4): 32-35. (in Chinese))
[11]谢江红.土石坝静力有限元分析[J]. 黑龙江科技信息, 2010, (15): 233. (XIE Jiang-hong. Static Finite Element Analysis of Earth-Rock Dam [J]. Heilongjiang Science and Technology Information, 2010, (15): 233. (in Chinese))
[12]彭文斌. FLAC3D实用教程[M]. 北京: 机械工业出版社, 2007. (PENG Wen-bin. FLAC3DProgramming Techniques and Practical Course[M]. Beijing: China Machine Press, 2007. (in Chinese))
[13]杜 斌, 吴梦喜. 土石坝分层填筑位移场修正的一种新方法[J]. 力学与实践, 2011, 33(4): 23-28. (DU Bin, WU Meng-xi. A New Approach for Modification of Displacement in Incremental Construction Analysis of Earth-Rock Dam[J]. Mechanics and Engineering, 2011, 33(4): 23-28. (in Chinese))
(编辑:陈 敏)
Influence of the Number of Simulated Filling Layerand Water Level on Dam Deformation and Stability
ZHOU Ai-hong, YUAN Ying, HE Guo-feng
(School of Prospecting Technology & Engineering, Shijiazhuang University of Economics, Shijiazhuang 050031, China)
To select the number of filling layer rationally and consider the influence of water level on deformation and stability is necessary in the numerical simulation of dam deformation and stability. Firstly, deformation and stability coefficient are selected as assessment indexes, and strength reduction method is introduced to calculate the stability coefficient of dam slope. Moreover, 3-D numerical model of layered filling is set up based on FLAC3Dto study the criteria of selecting the number of filling layer. Furthermore, on the basis of appropriate number of filling layer, the effect of water level on the deformation and stability of dam body is discussed. Results show that settlement is the predominant deformation and simulated settlements are closely related with the number of filling layer. Compared with settlement, horizontal displacement and safety factor are less sensitive to the number of filling layer which should be chosen according to the requirement of settlement precision; it is advised that the number of filling layer is not less than 10 layers, and the higher the dam, the more the number of filling layer should be. The horizontal displacement is more sensitive than the settlement and stability coefficient to water level of reservoir. These results are of guiding significance to determining the appropriate number of filling layer simulation.
layered filling; number of simulated filling layer; dam deformation; stability; settlement; stability coefficient; numerical siulation
2013-12-10;
2014-03-02
国家自然科学基金项目(41301015);国家大坝安全工程技术研究中心开放基金项目(NDSKFJJ1201);石家庄经济学院国家自然基金预研基金项目(SJY20123)
周爱红(1976-),女,河北唐山人,副教授,博士,主要从事岩土工程、地质灾害防治和设计的教学和科研工作,(电话)13230163159 (电子信箱)zhouaihong@sjzue.edu.cn。
10.3969/j.issn.1001-5485.2015.05.021
2015,32(05):110-114
TV641;TV311
A
1001-5485(2015)05-0110-05
