软土深基坑双排桩支护结构的影响因素分析

丁洪元,昌 钰,陈 斌

(中冶集团武汉勘察研究院有限公司,武汉 430080)

软土深基坑双排桩支护结构的影响因素分析

丁洪元,昌 钰,陈 斌

(中冶集团武汉勘察研究院有限公司,武汉 430080)

基于软土地区的某深基坑双排桩支护工程，采用有限单元法建立了三维仿真计算模型对双排桩的受力和位移特性进行计算，系统分析了双排桩排间距、桩径以及前后排桩长等影响因素对双排桩支护结构受力和位移的影响，得到该软土基坑工程双排桩支护结构的最佳排间距、桩径和桩长。结果表明：当双排桩桩径取0.8～1.0 m、排间距取桩径的3～4倍时，排桩的弯矩分布和桩身的位移比较合理，可以最大化地发挥双排桩的支护作用；相比于后排桩桩长，增加前排桩的桩长对提高支护结构的稳定性更有效。

深基坑；双排桩；支护结构；数值模拟；影响因素

1 研究背景

双排桩作为一种新型的深基坑支护结构，其支护体系的侧向刚度较大，能更加有效地限制围护结构的变形，保证基坑工程施工的安全性，目前已被运用于软土地区深基坑支护加固工程[1]和边坡治理工程[2]。

由于利用传统土压力计算方法估算双排桩支护结构上的土压力存在较大偏差[3]，双排桩尚无简单有效的设计方法[4]，众多学者对双排桩支护体系的受力变形特征进行了大量研究。何颐华等[5]根据双排桩结构体系的特点，认为连梁可以看成没有变形的刚体，只能产生平移而不产生转角，因而推出前后排桩顶的水平位移相等；杜秀忠等[6]利用不同程序和计算方法对支护结构的内力、位移进行对比，分析了某水闸基坑的双排桩结构；孙涛等[7]运用有限元对某双排桩支护基坑进行了排距的优化方案研究；王军等[8]同样运用有限元软件具体分析了排距对桩身内力和变形的影响；钱同辉等[9]采用有限元方法对框架式双排抗滑桩的桩土相互作用影响进行了计算分析；杨保全等[10]利用有限元对基坑开挖过程中双排桩的桩体位移进行了计算分析。史海莹等[11]研究了地基土模量随深度增加的情况下双排桩的受力特性；应宏伟等[12]基于弹性抗力法计算模型，利用有限差分方法的相关理论编制了新的计算程序，经过与实测数据的对比分析提出了较为合理的计算模型；聂庆科等[3，13]考虑到空间效应对深基坑双排桩支护结构计算的影响，提出了一种新的计算模型，并在此基础上分析了冠梁对双排桩支护体系的影响。这些研究从不同方面为双排桩的设计方案优化提供了必要的论证。

由于双排桩支护结构的影响因素众多，目前关于双排桩的研究大都采用数值仿真模拟方法，本文针对软土地区某基坑双排桩支护工程，利用有限元方法系统地分析双排桩的排距、桩径及前后排桩的桩长对双排桩结构的受力和变形影响，旨在为软土地区基坑双排桩结构的设计提供一定的参考和借鉴。

2 基坑双排桩工程概化模型

该深基坑工程位于滨海软土地区，基坑平面为矩形，面积约为80 m×30 m，开挖深度为6 m。基坑竖向支护方案采用双排钻孔灌注桩作为基坑支护结构，采用矩形布置，双排桩纵向间距为6 m。

利用有限元方法对该双排桩进行受力分析时，考虑到基坑工程对称性，建模时基坑内侧取一半宽度(即15 m)为研究对象；考虑到基坑双排桩模型的影响范围[14]，基坑双排桩外侧的影响宽度一般为基坑开挖深度的2～3倍；深度方向的影响范围一般为开挖深度的2～4倍。因此，本文取双排桩外侧的岩土体宽度为18 m，深度取基坑底部往下24 m，桩纵向计算范围取双排桩纵向间距的一半，即3 m；模型四周均按固定支座设置边界条件。基坑开挖深度为6 m，模拟过程分2步进行开挖，每步开挖深度为3 m。本文采用控制变量法分析双排桩的排距、桩径及前后排桩的桩长对双排桩结构的受力和变形影响，每次仅取1个变量作为影响因素，其余参数设为常量，计算工况见表1。

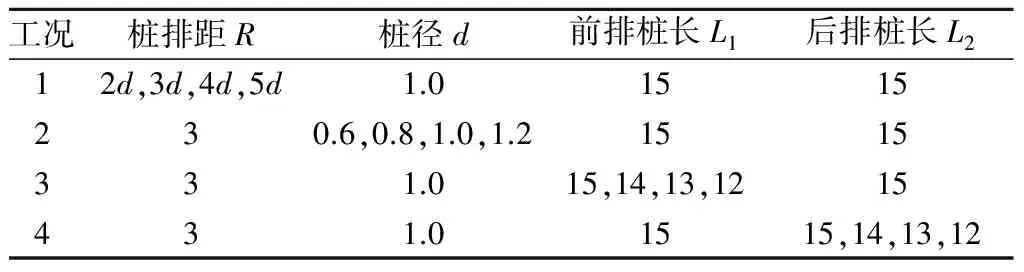
表1 基坑双排桩支护模拟工况

基坑双排桩支护结构的剖面见图1。由于双排桩桩体、桩顶的联系梁均为钢筋混凝土结构，刚度较大，因此选用线弹性本构模型进行模拟，其中混凝土中的钢筋采用刚度等效原理，等效为混凝土，双排桩桩身等混凝土材料的重度γ=25 kN/m3，弹性模量E=3.00×104MPa，泊松比ν=0.167。

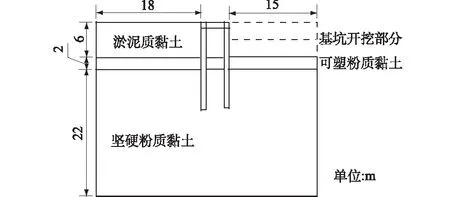
图1 基坑双排桩支护工程剖面示意

岩土体材料在受力过程中应考虑其弹塑性变形特性，为简化计算，岩土体材料选用理想弹塑性的本构模型，其屈服强度采用Drucker-Prager准则。根据工程场区地质钻探资料的岩土试验数据，选取模型岩土层的计算参数如表2。

表2 岩土体材料参数

3 排间距对双排桩的受力影响分析

为讨论前后排桩排距对双排桩受力的影响，本文采用控制变量法，即桩长、桩径均取为常数，仅考虑排距的变化，分别建立有限元模型进行受力分析。

本次分析过程，前后排桩长均取L=15 m，桩径d=1 m，前后排桩距R分别为2d，3d，4d，5d，基坑开挖后前后排桩所受的弯矩和产生的位移分别如图2和图3所示。

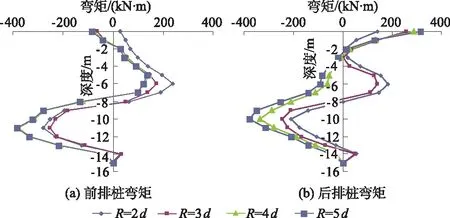
图2 不同排距下双排桩弯矩

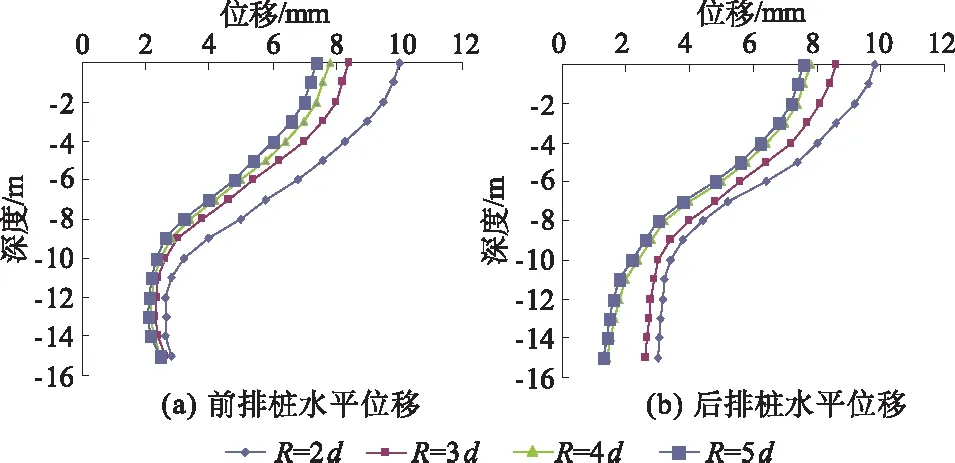
图3 不同排距下双排桩水平位移

由图2可以看出，当排距由2d增大到3d时，前排桩的弯矩值相差较明显，后排桩的弯矩值则变化较小；当排距由3d增加到4d时前后排桩的弯矩变化都比较大；当排距由4d增加到5d时，不论是前排弯矩值还是后排弯矩值差异都很小。

由图3可以看出，随着桩排距的增大，前后排桩的水平位移均逐渐减小。当排距由2d变为3d时，前后排桩位移的减少量比较大，前后排桩桩顶的位移都减少了1.5 mm左右；当排距由4d增大到5d时，前后排桩的位移变化量很小，可以认为超过4d时，增大排距对减少桩身的位移影响不大。

综合分析上述结论，当排距取为桩径的3～4倍时，排桩的弯矩分布和桩身的位移比较合理，可以最大化地发挥排桩的支护作用。

4 桩径对双排桩的受力影响分析

为研究桩径对双排桩体系的受力及位移影响，同样采用控制变量法，取前后排桩距为R=3 m，前后排桩长均取L=15 m，并假设前后排桩径d相同，分别取为0.6，0.8，1.0，1.2 m，建立有限元模型进行受力分析，基坑开挖后不同桩径下前后排桩所受的弯矩和产生的位移分别如图4和图5所示。

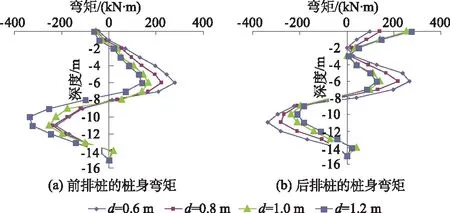
图4 不同桩径下双排桩弯矩

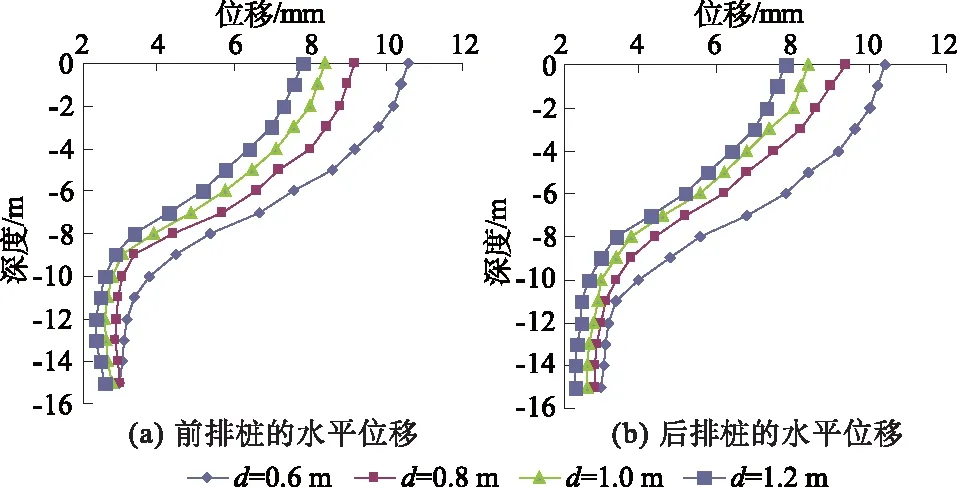
图5 不同桩径下双排桩水平位移

由图4(a)可以看出：在深度-8 m以上的桩身段，桩径越大，前排桩的正弯矩越小，最大正弯矩由d=0.6 m时的273 kN·m减小为d=1.2 m时的140 kN·m；而在深度-8 m以下的桩身段，桩径越大，前排桩身负弯矩绝对值越大，当桩径为0.6，0.8，1.0 m时，负弯矩变化并不大，但当桩径由1.0 m变为1.2 m时负弯矩绝对值有明显的增大。由图4(b)可以看出：桩径越大，后排桩桩身全长的正负弯矩绝对值均减小，说明桩径变大有利于后排桩桩身的整体受力，但也仅在一定范围内有明显效果，当桩径为1.2 m时，较桩径为1.0 m时的桩身弯矩变化并不明显。

由图5可以看出，随着桩径的增加，前后排桩桩体位移都在逐渐减小，说明增加桩径对提高支护结构的稳定性具有一定的作用，但随着桩径的逐渐增大，位移的减少量逐渐减小，表明当桩径增大到一定程度后，桩径对桩土体系稳定性的影响已不再是主要因素。当桩径由0.6 m增大到0.8 m时，位移的减小量最大，前后排桩桩顶的位移都减少了1.4 mm左右；随着桩径的增加，前排桩的桩端位移逐渐趋于稳定，而后排桩的桩端位移仍稍有减少。

因此，本文建议该类软土地区双排桩的桩径取为0.8～1.0 m较为合理。

5 桩长对双排桩的受力影响分析

进行双排桩支护结构设计时，考虑到工程实际的需要，经常会根据前后排桩实际受力和位移分布特点，来确定前后排桩的桩长，这就会导致在工程中出现前后排桩长不相等的情况。为了探究桩长对软土地区深基坑双排桩支护结构受力情况的影响，本节分别对前后排桩取不同的桩长建立有限元模型进行受力特性分析。

5.1 前排桩桩长对双排桩的受力影响

按照控制变量的方法，取前后排桩距R为3 m，前后排桩的桩径d均取1 m，后排桩的桩长L2为15 m，分别取前排桩的桩长L1为15，14，13，12 m进行计算。不同前排桩桩长情况下基坑开挖时，双排桩弯矩和位移计算结果如图6和图7所示。

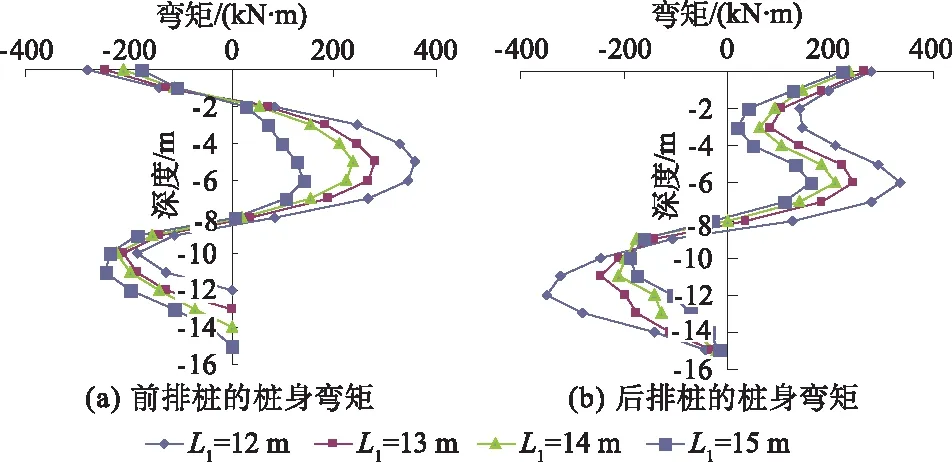
图6 前排桩桩长变化的双排桩弯矩

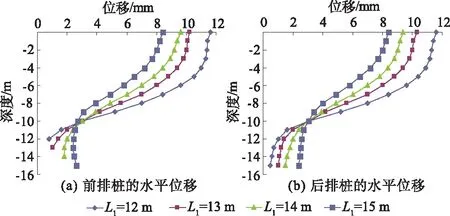
图7 前排桩桩长变化的双排桩水平位移

由图6可以看出，前后排桩的桩身正负弯矩的交接点为-8 m左右，-8 m以上的正弯矩，前后排桩的变化比较一致，前排桩桩长越长，前后排桩正弯矩都越小；-8 m以下的负弯矩，前后排桩变化趋势刚好相反，前排桩的桩长越长，其负弯矩绝对值越大，而后排桩的负弯矩绝对值越小。

由图7可以看出，随着前排桩桩长的变化，前后排桩的桩身位移都表现出了相同的变化趋势。前排桩的桩长越大，桩顶的位移越小，而桩端的位移越大，桩顶和桩端的位移差值越小，使桩身不容易因为上下两端的位移相差太大而导致失稳，越有利于结构的稳定。位移变化的交接点都在-10 m左右，在-10 m以下，前排桩的桩端位移变化较大，而后排桩的桩端位移逐渐趋于稳定。

5.2 后排桩桩长对双排桩的受力影响

同样按照控制变量的方法，前后排桩距R取为3 m，前后排桩的桩径d均取1 m，前排桩的桩长L1为15 m，分别取后排桩的桩长L2为15，14，13，12 m进行计算。不同后排桩桩长情况下基坑开挖时，双排桩弯矩和位移计算结果如图8和图9所示。

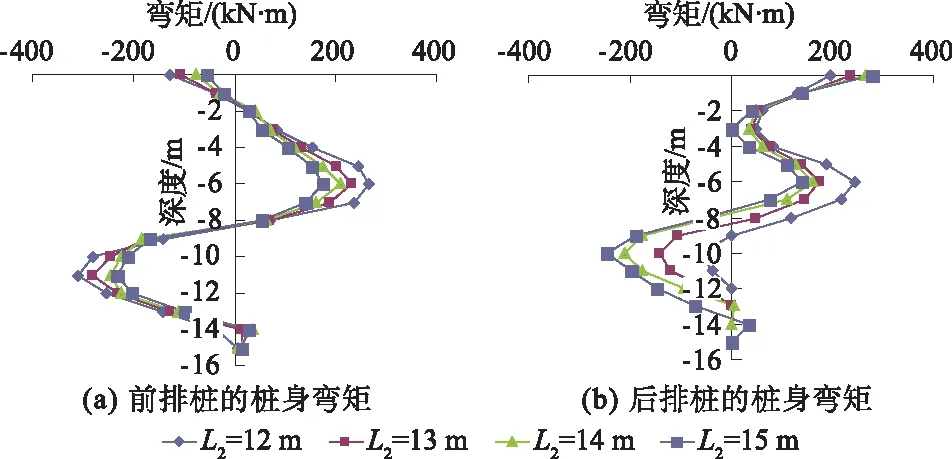
图8 后排桩桩长变化的双排桩弯矩

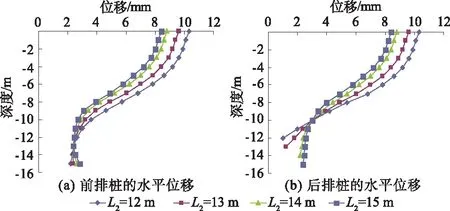
图9 后排桩桩长变化的双排桩水平位移

由图8可以看出，前排桩的桩身正负弯矩交接点为-8 m左右，后排桩桩长越长，正负弯矩绝对值越小；后排桩桩身的正负弯矩则表现出了一些不同，后排桩桩长越长，后排桩的正弯矩越小，而负弯矩绝对值越大。

由图9可以看出，随着后排桩桩长的变化，前后排桩的桩身位移都表现出了相同的变化趋势。与前排桩桩长影响规律一样，后排桩桩长越大，前后排桩的桩顶位移越小，桩端位移越大，使桩身不容易因为上下两端的位移相差过大而失稳，有利于结构的稳定。前排桩位移变化的交接点都在-13 m左右，而后排桩位移变化的交接点与前桩桩长变化时表现一致，都在-10 m左右。

综合考虑前后排桩桩长对整个支护结构弯矩和位移的影响，由于基坑开挖的作用，增加前后排桩的桩长都可以减少支护结构的整体位移，提高其稳定性；增加前排桩的桩长能更大程度地减少桩身的位移，比增加后排桩的桩长对提高支护结构的稳定性效果更好。因此，针对本工程建议前排桩桩长选择15 m，后排桩桩长为12 m。

6 结 论

本文针对软土地区某基坑双排桩支护工程，运用有限元方法，分析了双排桩的排距、桩径以及前后排桩的桩长等因素对双排桩受力变形的影响，主要得出了以下几点结论：

(1) 双排桩支护结构中，前后排桩的间距宜控制在(3～4)d的范围内，可有效的发挥前后排桩的抗滑能力以及控制前后排桩的变形，且排桩弯矩的分布较为合理。

(2) 随着桩径的增大，前排桩的正弯矩在深度-8 m以上的桩身阶段都有明显的减小，而在深度-8 m以下的桩身阶段，弯矩变化并不大；而后排桩桩身全长的正负弯矩均随桩径增大而减小，说明桩径变大有利于后排桩桩身的整体受力。

(3) 增加前后排桩的桩长都可以减少支护结构的整体位移，提高其稳定性；增加前排桩的桩长比增加后排桩的桩长对提高支护结构的稳定性效果更好。

[1] 付文光, 杨志银. 深圳地区基坑工程30年发展综述[J]. 岩土工程学报，2010, 32(增2): 562-565. (FU Wen-guang, YANG Zhi-yin. Summaries of Excavation Pit Engineering in Shenzhen in Recent 30 Years[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(Sup.2): 562-565. (in Chinese))

[2] 董必昌, 邱红胜. 双排桩对边坡稳定影响分析的仿真研究[J]. 武汉理工大学学报(交通科学与工程版)，2007, 31(3): 502-505. (DONG Bi-chang, QIU Hong-sheng. Simulation Study on Stability of Slope with Double-row Piles[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering)，2007, 31(3): 502-505.(in Chinese))

[3] 聂庆科, 胡建敏, 吴 刚. 深基坑双排桩支护结构上的变形和土压力研究[J]. 岩土力学, 2008, 29(11): 3089-3094. (NIE Qing-ke, HU Jian-min, WU Gang. Deformation and Earth Pressure of a Double-row Piles Retaining Structure for Deep Excavation[J]. Rock and Soil Mechanics, 2008, 29(11): 3089-3094. (in Chinese))

[4] 刘泉声, 付建军. 考虑桩土效应的双排桩模型及参数研究[J]. 岩土力学, 2011, 32(2): 481-486. (LIU Quan-sheng, FU Jian-jun. Research on Model and Parameters of Double-row Piles Based on Effect of Pile-soil Contact[J]. Rock and Soil Mechanics, 2011, 32(2): 481-486. (in Chinese))

[5] 何颐华, 杨 斌, 金宝森, 等. 双排护坡桩试验与计算的研究[J]. 建筑结构学报, 1996, 17(2): 58-66. (HE Yi-hua, YANG Bin, JIN Bao-sen,etal. A Study of the Test and Calculation of Double-row Fender Piles[J]. Journal of Building Structures, 1996, 17(2): 58-66. (in Chinese))

[6] 杜秀忠, 杨光华, 孙昌利, 等. 双排桩支护在某水利基坑中的应用[J]. 岩土工程学报, 2012, 34(增1): 490-494. (DU Xiu-zhong, YANG Guang-hua, SUN Chang-li,etal. Application of Retaining Structure with Double-row Piles in a Hydraulic Excavation[J]. Chinese Journal of Geotechnical Engineering，2012, 34(Sup.1): 490-494.(in Chinese))

[7] 孙 涛, 刘俊岩, 刘 燕. 双排桩支护排距的优化研究[J]. 岩土工程学报, 2012, 34 (增1): 616-620. (SUN Tao, LIU Jun-yan, LIU Yan. Optimal Row Distance of Retaining Structure with Double-row Piles[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(Sup.1): 616-620. (in Chinese))

[8] 王 军, 王 磊, 肖昭然. 双排桩支护排距的有限元分析与研究[J]. 地下空间与工程学报, 2005, 1(6): 1096-1099. (WANG Jun, WANG Lei, XIAO Zhao-ran. Analysis of the Interval between Double-row Piles by Finite Element Method[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(6): 1096-1099. (in Chinese))

[9] 钱同辉, 陈 芳, 程周炳, 等. 框架式双排抗滑桩结构性能研究[J]. 长江科学院院报, 2011, 28(11): 91-95. (QIAN Tong-hui, CHEN Fang, CHENG Zhou-bing,etal. Analysis on the Performance of Double-row Anti-Slide Frame-Piles[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(11): 91-95.(in Chinese))

[10]杨保全, 丘 滨, 陈先威. 双排桩结构特性及桩体位移有限元计算分析[J]. 长江科学院院报, 2009, 26(7): 52-55. (YANG Bao-quan, QIU Bin, CHEN Xian-wei. Deformation Analysis of Double Row Piles by Finite Element Method [J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(7): 52-55.(in Chinese))

[11]史海莹, 龚晓南. 深基坑悬臂双排桩支护的受力性状研究[J]. 工业建筑, 2009, 46(10): 67-71.(SHI Hai-ying, GONG Xiao-nan. Study on the Behavior of Cantilever Double-row Plies Supporting Deep Excavation[J]. Industrial Construction, 2009, 46(10): 67-71. (in Chinese))

[12]应宏伟, 初振环, 李冰河, 等. 双排桩支护结构的计算方法研究及工程应用[J]. 岩土力学, 2007, 28(6): 1145-1150. (YING Hong-wei, CHU Zhen-huan, LI Bing-he,etal. Study on Calculation Method of Retaining Structure with Double-row Piles and Its Application[J]. Rock and Soil Mechanics, 2007, 28(6): 1145-1150. (in Chinese))

[13]白 冰, 聂庆科, 吴 刚, 等. 考虑空间效应的深基坑双排桩支护结构计算模型[J]. 建筑结构学报, 2010, 31(8): 118-124. (BAI Bing, NIE Qing-ke, WU Gang,etal. A Calculation Model for Double-row-pile Retaining Structures in Deep Foundation Pit Considering 3D Effects[J]. Journal of Building Structures, 2010, 31(8): 118-124. (in Chinese))

[14]秦四清, 万林海, 汤天鹏, 等. 深基坑工程优化设计[M]. 北京:地震出版社, 1998. (QIN Si-qing, WAN Lin-hai, TANG Tian-peng,etal. Optimizing Design on Deep Excavation[M]. Beijing: Seismological Press， 1998. (in Chinese))

(编辑：黄 玲)

Factors Affecting Double-row Piles in Deep Soft Soil Foundation

DING Hong-yuan, CHANG Yu, CHEN Bin

(Wuhan Surveying-Geotechnical Research Institute Co., Ltd. of MCC, Wuhan 430080, China)

A 3D finite element model was established to calculate the forces and displacements of the double-row pile retaining structure of a foundation pit in soft soil area. The influences of row distance, pile diameter and pile length on the force and displacement of the structure are analysed in order to get the optimal pile row spacing, pile diameter and pile length. Results show that the distribution of bending moment and the displacement of pile are reasonable when the pile diameter is 0.8m-1.0m and the row distance is 3 to 4 times the pile diameter. Increasing the length of front pile is more effective to improving the stability of the retaining structure than increasing the length of back pile.

deep foundation pit; double-row pile; retaining structure; numerical simulation; influencing factor

2014-03-12；

2014-04-19

丁洪元(1969-)，男，四川广安人，高级工程师，主要从事岩土工程设计、施工、勘察等方面工作，(电话)13419604598(电子信箱)dinghongyuan69@163.com。

10.3969/j.issn.1001-5485.2015.05.020

2015,32(05):105-109

TU473

A

1001-5485(2015)05-0105-05