基于马尔科夫链的混流装配线缓冲区配置优化研究*

曹振新，鄂世举，焦卫东，周 武

(浙江师范大学 工学院，浙江 金华 321004)

基于马尔科夫链的混流装配线缓冲区配置优化研究*

曹振新，鄂世举，焦卫东，周 武

(浙江师范大学 工学院，浙江 金华 321004)

为提高混流装配线物流系统的可靠性，在各工位间需设置缓冲区。缓冲区容量是影响生产线性能指标的重要因素，在分析缓冲区功能的基础上，提出了生产线缓冲区的类型和结构，建立了自动导引车和自动化仓库存取系统构成的物流系统工作流程，利用马尔科夫链状态转移方程建立了基于AGV和AS/RS的装配线闭环物流系统数学模型，分析了缓冲区容量参数、AGV数量及生产线性能指标。实例计算表明，该模型方法与物流系统参数的正确性，满足了混流装配线对物流配送系统的要求。

马尔科夫链；混流装配线；缓冲区容量；排队论

客户的多样化需求促使制造型企业从传统的大规模生产方式向多品种、小批量生产方式转化。利用混流装配线(Mixed Model Assembly Line，MMAL)，可实现在同一条生产线上装配多种不同型号、数量，但工艺基本相似的产品，该方法在汽车和家电等行业中得到了广泛应用[1]。流水线的缓冲区配置是生产线设计时应考虑的重要因素。缓冲区不仅可用于存储在制品WIP，还能进行在制品重排，使得生产线具有良好的柔性。缓冲区配置问题(Buffer Allocation Problem，BAP)就是将一定数量的缓冲区分配到生产线的工位间，使得整条生产线顺利运行。物料处理延迟和缓冲区容量大小设置不合理都会影响整个装配线的正常运行。若缓冲区太小会导致工位堵塞，过大又会导致工位空闲和时间延误[2]。无论工位空闲还是工位堵塞，都会使生产线生产能力不平衡，出现各工位作业负荷不均，严重影响生产线的生产效率和可靠性；因此，配置合适的缓冲区是生产线设计中的一个重要而复杂的问题。

国内外学者对混流装配线的研究主要集中在作业平衡与产品排序问题上，并发表了很多学术论文；但对生产线缓冲区的配置与容量优化方面却研究较少。Michael等用排队模型建立多工位有限缓冲区的装配流水线生产率最大化模型，评估了两工位子装配线的生产性能。Fulya等用人工神经网络算法对装配线缓冲区容量进化优化配置和仿真分析[3]。Saeed等研究了有限容量排队网络的多类、多级装配系统交货时间优化问题，假设排队网络工位的装配工序时间互相独立，且服从指数服务概率分布，利用马尔可夫过程概念建立了任何类型产品订单接受时间和成品交货时间的系统微分方程[4]。MacGre等研究了单台服务器基于有限缓冲区的M/G/1/K排队网络性能[5]。国内的谭明等建立了基于有限缓冲区的生产线可靠性模型，并对生产线的转移状态和可靠性进行了分析，得到了生产线不同状态间的状态转移概率的计算方法[6]。华中生建立了考虑随机加工时间的非均匀节拍生产线的缓冲库存容量设计模型，提出了缓冲库存最优设计的一些结构特性[7]。高贵兵建立了基于马尔科夫过程原理的混流装配线可靠性模型，推导出装配线可用度与缓冲区容量之间的关系[8]。孟凡力根据随机原理提出了缓冲区被充满概率和缓冲区容量之间的函数关系，采取递进算法算出整个装配系统各个工位之间的缓冲区容量[9]。

综上所述，目前针对串/并联生产线缓冲区(BUFFER)容量设计方法大多过于理论化。如何使缓冲区有足够的空间存放在制品，同时避免因缓冲区设置不当引起物流中断是非常重要的。排队网络是设计与分析生产线的常用方法，但应用排队网络解决生产线“饥饿”与“阻塞”现象的有限缓冲区配置问题却较少。应用排队网络模型研究装配线的缓冲区配置优化问题，可将该类物料运输系统看作随机服务系统，每个装配工位/站是排队网络的一个节点。自动化存取系统(Automatic Storage and Retrieval System，AS/RS)也叫立体仓库缓冲区，其缓冲区自动化程度高，重新排序工件性能好，易于实现混流生产，本文对该类缓冲区进行建模优化研究。

1 问题描述

由于混流装配线由输送带连接若干个装配作业单元所构成，各工位间会存在各种不确定性和干扰因素，因此需要一定的保护能力来平衡不确定性，使生产具有一定的柔性和鲁棒性。这种保护能力在多数情况下可通过在生产线中加入缓冲区来实现。若缓冲区太小，容易发生堵塞故障；若容量太大，会增加缓冲区的成本、维护费用及在制品的流动时间，造成物流中断[10]。装配生产线上都会有瓶颈工位，在瓶颈工位之前容易出现工位堵塞，在瓶颈工位之后容易出现工位空闲，使生产线系统的可靠性和整条生产线的效率降低。根据TOC理论，在实际装配生产线设计时，选择在生产系统中的几个关键的瓶颈工位之前设置缓冲区。混流装配线简化工艺流程模型如图1所示[11]。

图1 混流装配线简化工艺流程模型

在产品总装的混流装配过程中，各装配工位在装配时刻需要判断工位旁有无相应的零部件。如没有足够相应类型的零部件数量，则停工待料。在瓶颈工位之前设置在制品缓冲区，可提高整条生产线的可靠性。本文主要讨论混流装配流水线相邻关键工位间的基于安全提前期的缓冲区设计问题，不存在损失制和机器故障。

缓冲区按照容量大小来分，可分为无限容量缓冲区、大缓冲区和小缓冲区。无限容量缓冲区假设存储在缓冲区上的工件的数量没有限制，是一种纯理论化的缓冲区；大缓冲区一般指容量较大的有限缓冲区，可实现在制品的重新排序，大多应用在汽车等大型机械装备混流生产线中；小型缓冲区是设置在两装配工位间的有限临时存储区，只需周期性配送补货。自动存取缓冲区采用了立体仓库的结构形式，每个区域由若干运输小车(Automated Guided Vehicle，AGV)完成存取工作。AS/RS运行和处理速度快，并可实现对工件的重新排序，提高了劳动生产率，降低了劳动强度，使企业物流更趋合理化。

2 基于AGV和AS/RS的装配线物流调度系统

AS/RS是采用自动化存取输送设备进行存取仓库的物料作业，是装配生产过程中的物流中心。其主要由存储货架及托盘、自动导引车、堆垛机和自动控制系统所组成。存储货架由1个或多个存储巷道组成，巷道两边是存储货架，每个巷道有1个堆垛机服务。AS/RS具有拾取和放置(pickup-and-deposit)工位的存储系统，该存储系统能够高效和精确地完成存取操作。AGV装备有自动导引装置，能够沿设定路径行驶的物料运输小车在汽车生产线中得到了广泛的应用。将工位缓冲区补充库存的请求当作需要服务的顾客，AGV为这些请求服务，多台AGV可作为一组服务器；各工位缓冲区为各工位服务，将其作为另一组服务器。对于每一个服务器，假设服务请求的到达和离去都是Poisson过程，各节点的服务时间呈指数分布。AGV系统增加了装配系统的柔性，改善了操作人员的作业环境，提高了装配系统的智能和自动化程度。

当1个工位缓冲区的库存小于安全值时，则该工位发出要求补充缓冲区库存消息，相应的缓冲区即成为发出一个需要AGV的信号，该请求进入以AGV为服务器的队列。当AGV完成一个请求后，该请求即成为一个安全的缓冲区。缓冲区队列的服务时间对应于缓冲区相邻2次补充库存的间隔时间。工位缓冲区与AGV之间可简化为具有2组服务器的闭环排队网络模型，AGV调度系统是一个M/M/C系统。具有AGV、AS/RS以及各工位具有缓冲区的装配系统自动化程度高、柔性大，适合大批量定制生产模式。一般AGV-AS/RS系统由多辆AGV和AS/RS构成(见图2)，其物流调度系统流程如下。

1)当工位缓冲区监测到剩余库存量达到安全补料库存时，通过通信设备发出物料补充信号到物流管理中心，形成出库任务。

2)物流调度系统将需要补充的物流种类和数量发送到AS/RS管理系统，形成堆垛机的对应任务排列。

3)AS/RS管理系统根据其出货要求，将请求的AGV信息发送到物料中心调度系统，根据各AGV的状态和需要的完成时间，确定为此请求服务的AGV。

4)AGV按先到先服务的原则装载物料，并送至请求工位的缓冲区AS/RS。物料到达后，AGV将空箱送回到回收站，并回到指定停车点。

5)如果该AGV没有其他任务，则回AGV站。物流调度系统把任务执行情况上报物流管理系统，至此完成一个物料出库的服务周期。

6)物流调度系统根据物料入库申请和库存信息形成入库任务，并由相应的堆垛机完成入库任务，由AGV完成一个物料入库的服务周期。

从上述物流调度系统流程可见，将基于AGV和AS/RS的物流系统视为一个随机排队服务系统，可建立该系统的排队网络模型，并分析AGV数量与系统性能指标之间的关系，如AGV的利用率、平均延迟时间及工位缓冲区的可靠性等之间的关系。假设装配系统总体布局和AS/RS结构参数已经确定，基于AGV和AS/RS的物流系统设计的主要内容是：1)AS/RS缓冲处理能力(出库能力)计算；2)确定AGV的调度规则；3)确定AGV的数量。

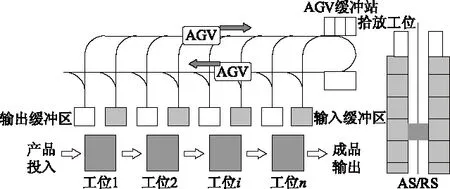
图2 基于AGV和AS/RS构成的物流系统

3 模型构建

闭环排队数学模型的假设条件如下。

1)生产线有m个缓冲站，缓冲站i的物料需求(顾客)是参数为λi的Poisson流。

2)物流排队系统有AGV运输小车n台，服务时间独立，且服从参数u的负指数分布。

3)设λ为到达率，u为服务率，出库物料任务队列按先入先出(FIFO)原则接受空闲AGV小车的运输服务，不存在损失制。

4)在时刻t正在装配的工位在(t,t+Δt)内，缓冲区库存由大于安全值变为等于安全值的概率为：λΔt+o(Δt)。

5)在时刻t正在接受AGV服务的工位缓冲区库存转变为安全值的概率为：μΔt+o(Δt)。

6)各工位的库存状态信息(库存≥安全值)分布相互独立。

自动化立体仓库输送和自动引导车AGV运输系统为随机服务系统。{X(t),t∈T}是一个随机过程，{X(t),t∈T}在t0时刻所处的状态为已知时，与它在时刻t>t0之前所处的状态无关。设马尔可夫链X={X(t),t≥0}，状态空间S={0,1,2,…}。显然，{X(t),t≥0}是一个状态离散、参数连续的有限齐次马尔可夫过程。容易证明，{X(t),t≥0}是一个生灭过程。系统状态转移图如图3所示。

图3 系统状态转移图

用Xt表示该系统在时刻t库存量≤安全值的工位数(已发出补料请求，尚未得到补料的工位)，k=0,1,2,…,m-1。则其状态转移概率矩阵满足：

P(Xt,n+1=kn+1|Xt,1=k1,Xt,2=k2, …,
Xt,n=kn) =P(Xt,n+1=kn+1|Xt,n=kn)

(1)

式1表明该过程接下来的时间状态可以完全由当前的状态决定，而与过去的状态无关，即具有马尔可夫性。容易证明，{X(t),t≥0}是一个生灭过程。由生灭过程的定义有：

则根据生灭过程的相关性质，推导出该物流系统马尔可夫过程{X(t),t≥0}的平稳分布概率为：

(2)

pk=

(3)

请求自动运输小车服务的工位数(平均队长)：

(4)

自动运输小车请求的平均到达率：

(5)

AGV请求的平均等待时间：

(6)

AGV平均延迟时间：

(7)

自动运输小车AGV的利用率：

UAGV=1-p0

(8)

工位缓冲区系统的可靠性：

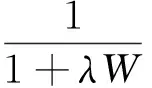
(9)

4 实例计算与分析

设有一个基于AS/RS的混流装配线系统，有4台AGV为40个工位的缓冲区补充零部件。设AGV完成一次请求任务的平均时间为10 min，每个工位平均每小时补充一次物料。根据上述排队网络模型，则该过程的稳态分布p(k) = (0.032 8, 0.109 3, 0.177 5, 0.187 4, 0.144 5, 0.108 3, 0.079 0, 0.056 0, 0.038 5, 0.025 6,0.016 6, 0.010 4, 0.006 3, 0.003 6, 0.002 1, 0.001 1, 0.000 6, 0.000 3, 0.000 1, 0.000 1,0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 1, 0.000 0, 0.000 0,0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 0, 0.000 1, 0.000 0, 0.000 0,0.000 0)。横坐标为工位的数量k，纵坐标为平稳分布值p(k)，如图4所示。

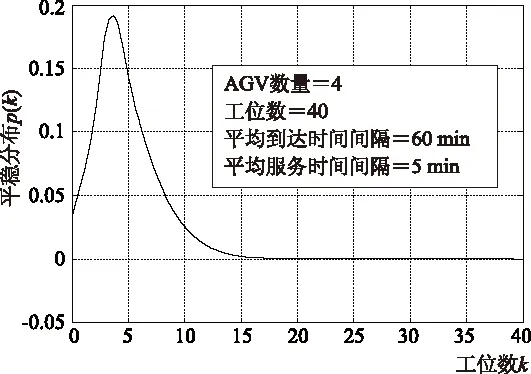
图4 状态的平稳分布图

由式5计算可得到，请求AGV服务的工位数期望(平均队列长度)为4.0；由式6计算可得到，自动小车AGV的请求平均到达率为0.017；由式7计算可得到，请求的平均等待时间为6.70 min；由式8计算可得到，平均延迟1.70 min；由式9计算可得到，AGV的利用率为0.97；由式10计算可得到，工位缓冲区的可靠性为0.90。当AGV的数量变化时，系统性能指标与AGV数量的关系如图5所示。

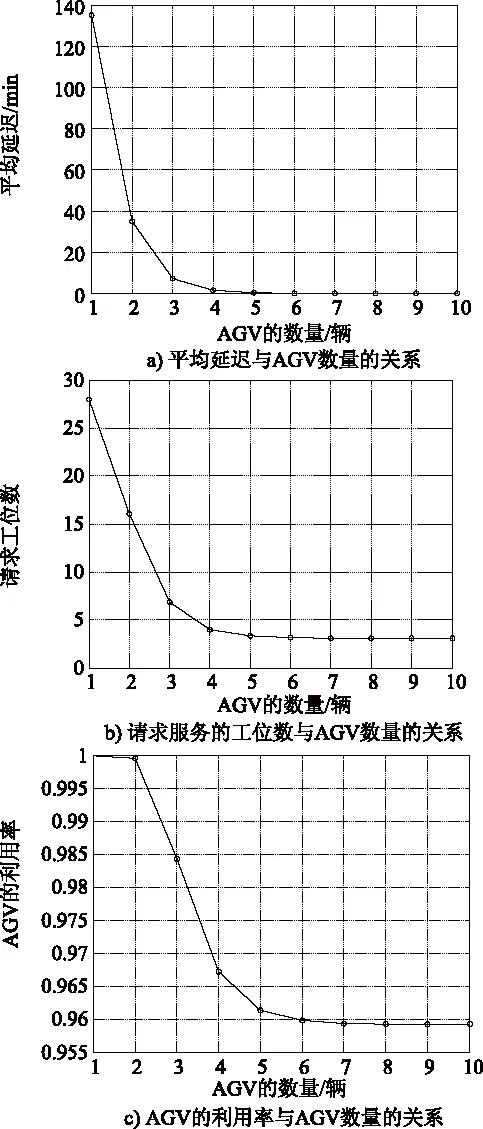
图5 物流系统性能与AGV数量之间的关系

5 结语

多品种混流装配提高了制造系统柔性和企业的精益化生产。缓冲区在复杂的装配系统中起着重要作用，可为系统提供一定的保护能力来平衡各种干扰和不确定性。论文针对混流装配线缓冲区容量优化问题进行研究，根据容量大小和结构形式对缓冲区进行了分类，建立了缓冲区容量和结构设计方法。在阐述AGV和AS/RS组成的自动存取物流系统工作流程的基础上，建立了基于马尔科夫链的物流系统的随机排队网络模型，证明了该模型的可行性和正确性。经计算得到系统稳态的分布及条件排队等待工位数量与等待时间数据，分析了该物流系统的相关性能及概率特性，证明了该方法的可行性。因实际设计生产线缓冲区时要考虑的因素较多，缓冲区容量的多目标优化配置仍需深入研究。

[1] 曹振新.混流汽车总装过程的物料协同配送与管理信息系统研究[J]. 制造业自动化，2008(12): 25-29.

[2] Michael M. Queueing-model based analysis of assembly lines with finite buffers and general service times[J]. Computers & Operations Research, 2008(35):2520-2536.

[3] Fulya A, Berna D. Buffer allocation and performance modeling in asynchronous assembly system operations: An artificial neural network meta-modeling approach[J]. Applied Soft Computing, 2007(7):946-956.

[4] Saeed Y, Siamak N. Lead time control in multi-class multi-stage assembly systems with finite capacity[J]. Computers & Industrial Engineering, 2013(66):808-817.

[5] Smith J M. Properties and performance modeling of finite buffer M/G/1/K networks[J]. Computers & Operations Research, 2011(38):740-754.

[6] 谭民, 疏松桂. CIMS生产线中缓冲区状态及可靠性分析[J]. 自动化学报, 1994, 20(3): 271-277.

[7] 华中生.非均匀节拍生产线缓冲库存设计的结构特性[J]. 运筹与管理, 1994, 3(2): 29-33.

[8] 高贵兵，岳文辉，张道兵，等. 基于马尔科夫过程的混流装配线缓冲区容量研究[J]. 中国机械工程, 2013, 24(18): 2524-2528.

[9] 孟凡力,谈大龙,黄雪梅.装配系统中缓冲区容量的研究[J]. 计算机集成制造系统，2005，11(11)：1609-1616.

[10] 秦永法, 赵明扬.具有AGV和AS/RS的装配线物流系统分析[J]. 机械设计与制造, 2005(6): 166-168.

[11] 李修琳，鲁建厦，柴国钟，等. 基于混合遗传算法的混流混合车间协同调度问题[J]. 中国机械工程, 2012, 23(8): 935-940.

*浙江省自然科学基金资助项目(LY12G01004)国家自然科学基金资助项目(51405450)

责任编辑郑练

P92大口径厚壁无缝钢管再获国家支持

2015年6月1日，在工业和信息化部举行的2014年工业转型升级强基工程合同签约仪式上，中国兵器工业集团公司内蒙古北方重工业集团有限公司董事长、党委书记李建平与工信部规划司司长肖华正式签订国家强基工程《超超临界火电机组P92大口径厚壁无缝钢管工程项目》合同书，北重集团获国家支持资金4980万元。北重集团生产的P92钢管在力学性能、显微组织、无损检测等主要技术指标方面与国外先进产品基本相同，国产钢管的工艺质量水平已经达到国际先进水平，部分指标甚至已经超过国际先进水平，能够满足不同标准体系的技术指标要求，完全可以替代进口P92钢管使用。

——摘自中国兵器工业集团公司网

OptimizationofBufferCapacityforMixedModelAssemblyLinebasedonMarkovChain

CAO Zhenxin, E Shiju, JIAO Weidong, ZHOU Wu

(College of Engineering, Zhejiang Normal University, Jinhua 321004, China)

The buffer is introduced between each station in order to improve the reliability and the productivity of logistics system for the mixed assembly line. Buffer capacity is an important factor affecting the production line performance indicators. The type and structure are elaborated based on analyzing the buffer function. The working procedure of the material handling system with the automatic storage retrieval system and automated guided vehicle is built. The closed-loop queuing network model using is developed using queuing theory based on Markov process. The buffer capacity and the states of work station are analyzed. Examples of calculations show that the model and buffer settings are reasonable which could meet the requirements for the mixed assembly line logistics system.

Markov chain, mixed model assembly line, buffer capacity, queuing theory

TP 29

：A

曹振新(1976-)，男，博士，副教授，硕士生导师，主要从事工业工程与管理和计算机集成制造等方面的研究。

2014-12-09