液力透平进口截面对水力损失及速度矩的影响

史广泰，杨军虎

(兰州理工大学能源与动力工程学院，甘肃 兰州 730050)

·能源与环境·

液力透平进口截面对水力损失及速度矩的影响

史广泰，杨军虎*

(兰州理工大学能源与动力工程学院，甘肃 兰州 730050)

为减小液力透平各过流部件的水力损失，提高液力透平的效率，在不同蜗壳进口截面下将一单级液力透平蜗壳的基圆作为一环线，计算沿该环线的切向速度值，根据基圆半径计算出相应的速度矩，并在环线上分别设置4个监测点，利用ANSYS软件计算监测点处的速度矩随流量的变化规律，最后研究蜗壳进口截面对各过流部件水力损失的影响。结果表明：所选液力透平的蜗壳最佳进口直径为65 mm，改进后液力透平的效率比原设计下的效率提高了1.83%，且在该蜗壳进口下叶轮进口的速度矩波动幅值最小；随着蜗壳进口直径的增加叶轮进口的速度矩逐渐减小，蜗壳收缩管的收缩率逐渐增加，收缩管中的水力损失逐渐减小。

液力透平；蜗壳；水力损失；速度矩

液体流动前后是相互影响的，即前面的流动状态对后面零件内的液体流动有很大影响；因此，液力透平内液体流动状态既依赖于每个过流元件的形状和尺寸，又依赖于过流元件的共同组合。为使液力透平过流部件间相互影响小，就必须保证叶轮内相对运动和透平体内的绝对运动是稳定的；而在非设计工况下，液力透平内流动必然是非定常的，速度场和压力场的随时变化会带来附加的水力损失。液力透平内的水力损失主要包括摩擦损失、冲击损失、分离损失和二次流损失等[1]。

目前，在离心泵中学者们对叶轮几何参数、叶片形状、叶片设计方法以及蜗壳截面形状和几何参数均有研究[2-6]。而在液力透平中主要对叶轮几何参数、叶片形状和叶片设计方法进行了研究[7-12]，较少对蜗壳进行研究。对液力透平而言，流体首先通过蜗壳，之后才流经叶轮，离心泵蜗壳的出口变为液力透平蜗壳的进口，离心泵蜗壳的进口变为液力透平蜗壳的出口，因此蜗壳的形状和几何尺寸对液力透平性能的影响较大。在液力透平中，不同的蜗壳进口截面对应不同的蜗壳进口收缩率，收缩率越大，能量损失越小，因此在液力透平中存在一最佳的蜗壳进口直径，使液力透平具有较好的性能。蜗壳进口截面的重新设计将对提高液力透平的性能具有重要意义。

本文以一单级液力透平为研究对象，利用ANSYS软件，采用数值计算的方法计算出蜗壳基圆上各个点处的速度矩以及液力透平各过流部件的水力损失。

1 计算方法的提出

在离心泵中蜗壳扩散管的作用在于降低速度，转换为压力能，同时减小排出管路中的损失[13]；但当离心泵用作透平时扩散管变为收缩管，这时收缩管的作用将变为降低压力，转换为动能，驱动叶轮旋转[14-15]。

由于收缩管的能量损失小于扩散管的能量损失，随着收缩管收缩率的逐渐增加，收缩管中的能量损失逐渐减小，当直接将离心泵的蜗壳用于液力透平时，所获得的液力透平效率并不是最佳效率；因此，为了能够提高液力透平的效率，也需要对液力透平的蜗壳收缩管进行重新设计。本文将在不同蜗壳进口截面下将单级液力透平蜗壳的基圆作为一环线，计算沿该环线的切向速度值，根据基圆半径计算出相应的速度矩，并在环线上分别设置4个监测点，利用ANSYS软件计算这些监测点处的速度矩随流量的变化规律，最后研究蜗壳进口截面对各过流部件水力损失的影响。由于第八断面是不规则形状，所以从进口过渡到出口，其间的断面应逐渐变化，以保证整个壁面光滑。

2 液力透平的主要参数

本文研究对象为一单级液力透平，其设计参数为：流量123 m3/h,水头147 m，转速2 900 r/min，比转速46，叶轮旋转方向为逆时针。图1为所选模型的主要几何参数。

图1 所选模型的几何参数

由于蜗壳进口截面为圆，所以本文在所选研究对象的基础上通过增大蜗壳进口直径(简称大蜗壳进口)和减小蜗壳进口直径(简称小蜗壳进口)来研究蜗壳进口直径D5分别为50、65、80和100 mm时该液力透平沿环线的速度矩和各过流部件的水力损失。

3 数值计算

本文采用非结构网格进行划分，且进行了网格无关性研究，当网格总数大于100万时，效率的变动范围小于0.5%，因此网格数大于100万时较合适，本文的总网格单元数为102万8 967，节点数为20万504。利用ANSYS-FLUENT软件采用基于压力的求解器，以稳态法求解。透平进口边界设为速度进口，出口设为压力出口，为了研究隔舌处和距离收缩管较近处速度矩的变化，在基圆上分别设置监测点1和2，为了研究不同收缩率对距离收缩管较远处速度矩的影响，在基圆上均匀设置两监测点3和4，如图2所示。计算收敛标准设为10-5，壁面粗糙度设为50 μm，采用SIMPLEC算法进行计算，输送介质为常温清水，湍流模型选用k-ε湍流模型，过流部件动静结合部位设置为interface连接。

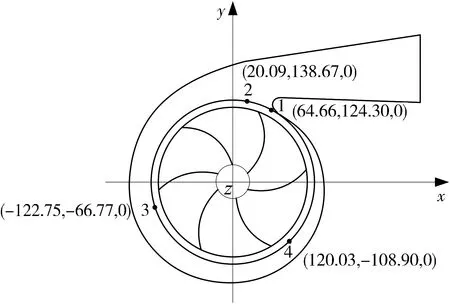
图2 基圆上的监测点

4 结果分析

4.1 蜗壳进口对速度矩的影响

图3为最优工况时不同蜗壳进口直径下液力透平速度矩的变化情况。表1为最优工况下各个蜗壳进口截面下的最大速度矩。由图3可以看出，在D5=65 mm时的最大波动幅值最小，因此在蜗壳进口直径等于65 mm时，该液力透平的叶轮进口速度分布较其他进口截面均匀，在小蜗壳进口下随着蜗壳进口直径的增加叶轮进口的速度矩逐渐减小，这是因为在同一流量下蜗壳进口直径越大，液流速度越小，因此速度矩也越小。由图中可以看出在横坐标数值分别为-120°、-60°、0°、60°和120°时波动幅值最大，这是因为这些位置为叶片的进口位置，所以由于叶片的影响使该处速度矩波动幅值增大。由图3还可以看出原设计工况下基圆上的速度矩最小，即当直接将离心泵的蜗壳用于液力透平中时叶轮进口的速度最小；因此，要减小速度矩的波动除了选择最佳的蜗壳进口截面外，还必须在叶轮进口前添加导叶使液流在蜗壳中均匀、对称地进入下一个过流部件，这样更有利于改善蜗壳出口速度分布的均匀性[16]。

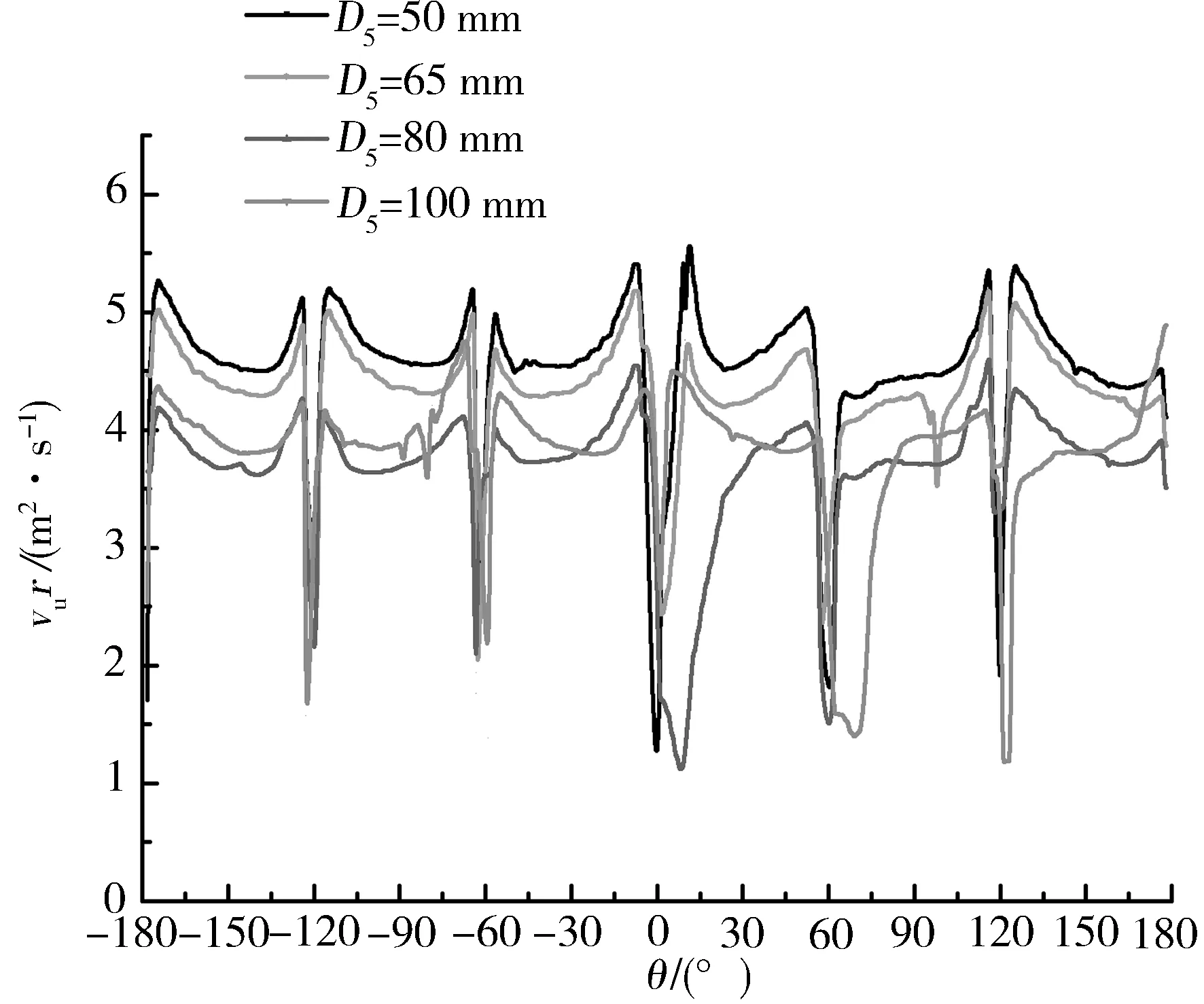
图3 蜗壳进口直径对速度矩的影响

表1 最优工况下的最大速度矩

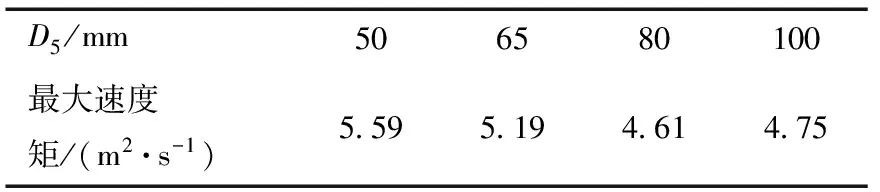
D5/mm506580100最大速度矩/(m2·s-1)5 595 194 614 75

图4为不同流量下横坐标数值分别为-130°、-15°、15°和110°时速度矩的变化曲线，即分别为图2中监测点3、2、1和4处的速度矩随流量的变化规律。由图4可以看出距离蜗壳收缩管较远处监测点的速度矩随流量的增加而增加，距离蜗壳收缩管较近处监测点的速度矩在小流量时随流量的增加而减小，随着流量的继续增加，速度矩反而开始增加。

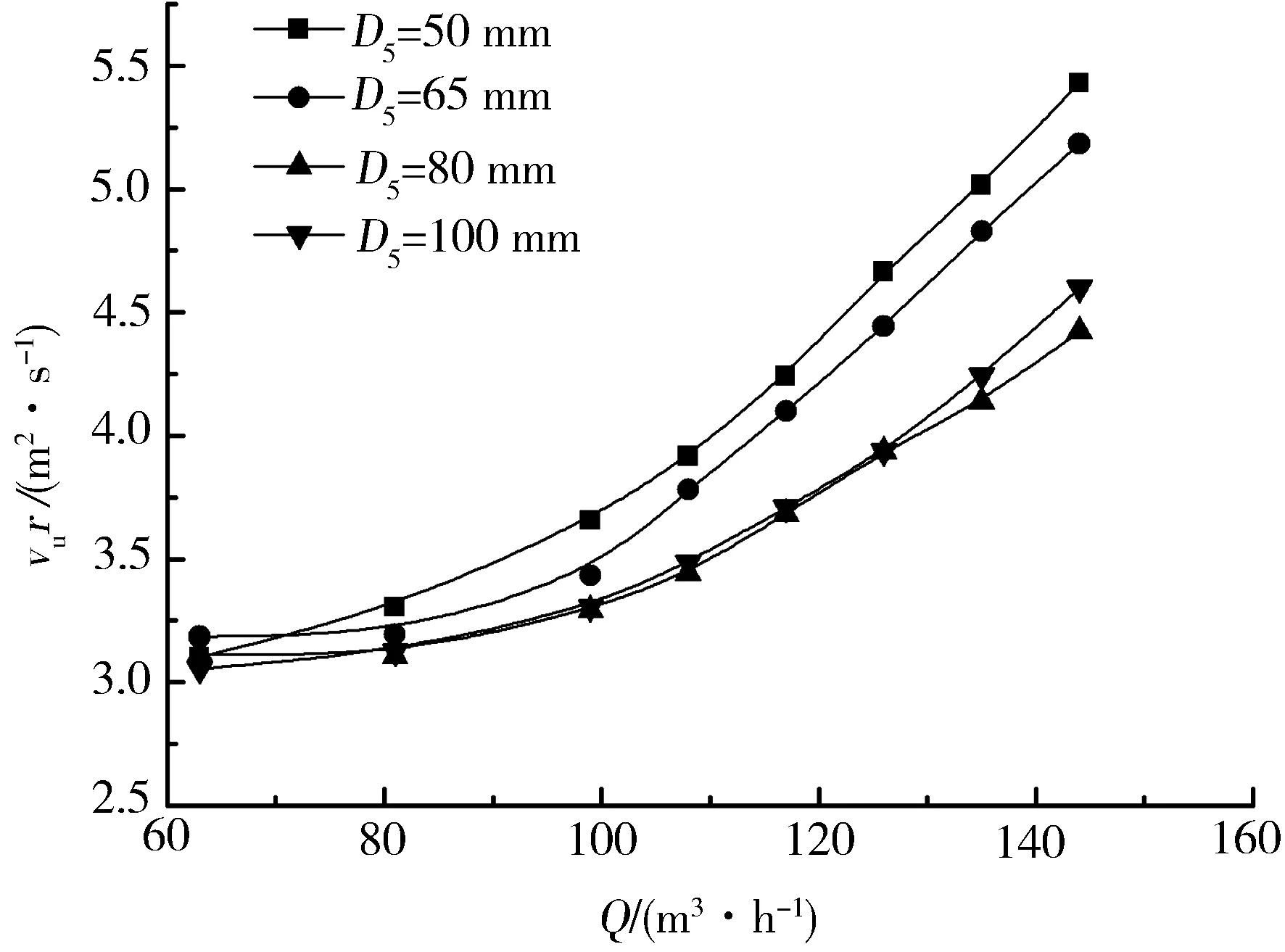
(a)θ=-130°

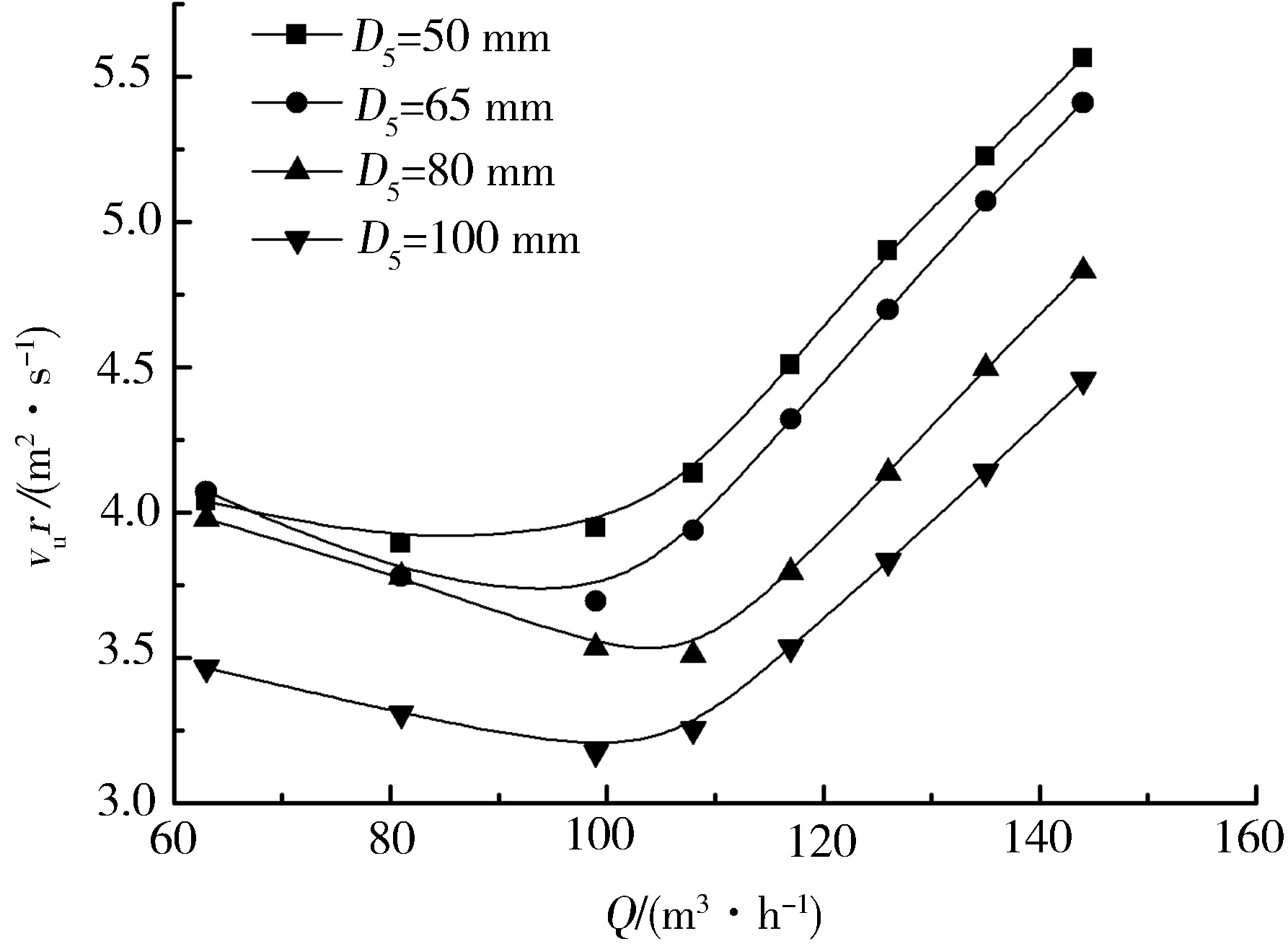
(b)θ=-15°

(c)θ=15°

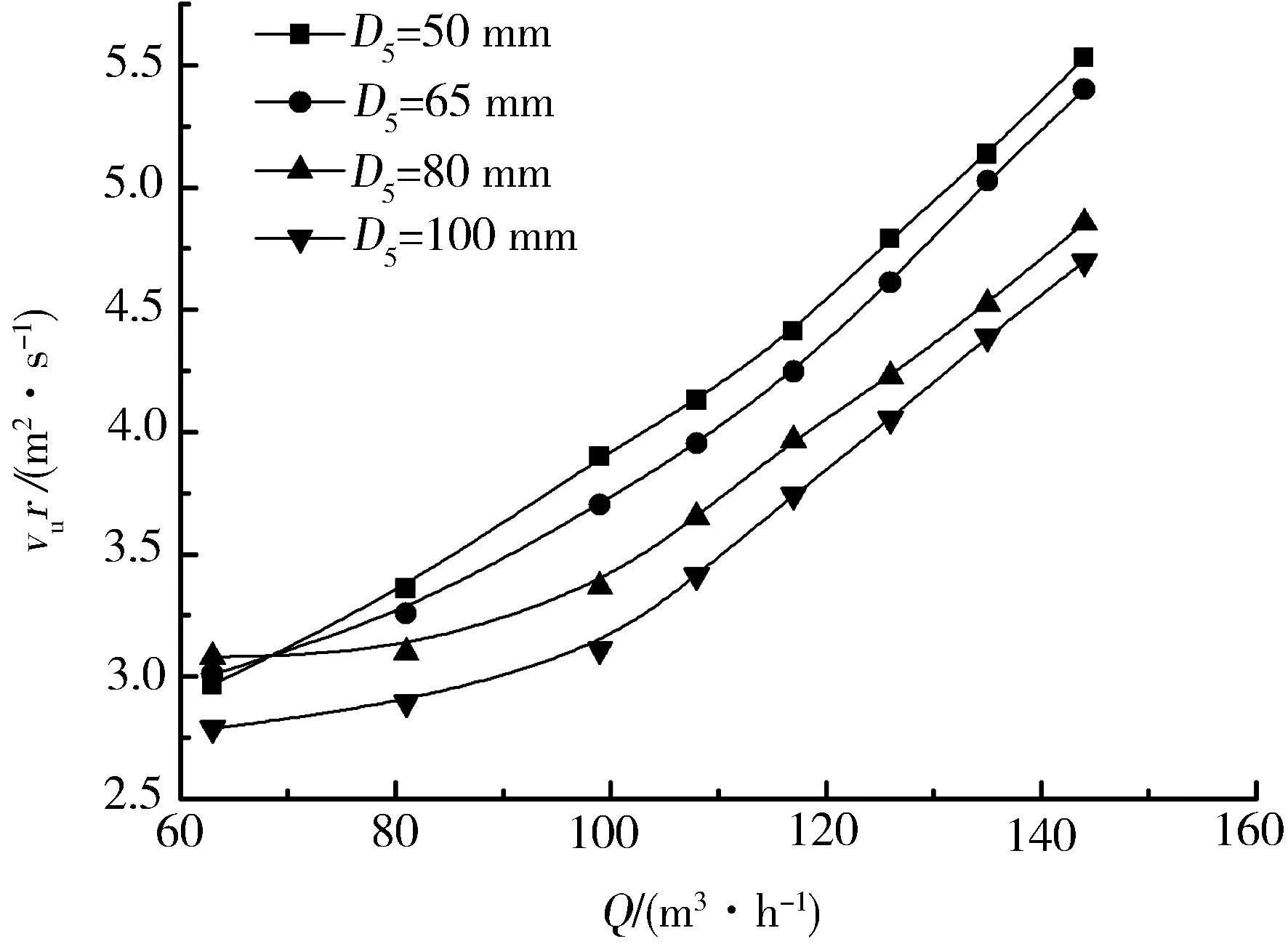
(d)θ=110°

对比图4中各图，可以看出D5=50 mm时的速度矩最大，距离蜗壳收缩管较远处大蜗壳进口下的速度矩相差较小，而距离收缩管最近的监测点2，即θ=-15°处蜗壳进口直径等于100 mm时的速度矩最小，监测点1，即θ=15°处蜗壳进口直径等于80 mm时的速度矩最小。从图4(c)中可以看出蜗壳进口直径等于65 mm时速度矩随流量的变化最小，且由于θ=15°处为隔舌位置；因此，当蜗壳进口直径等于65 mm时隔舌处叶轮进口的速度随流量的变化较小。

4.2 水力损失

水力损失是指由于介质具有黏性而在流动过程中引起的压力损失。图5为各过流部件中的水力损失随流量的变化曲线。

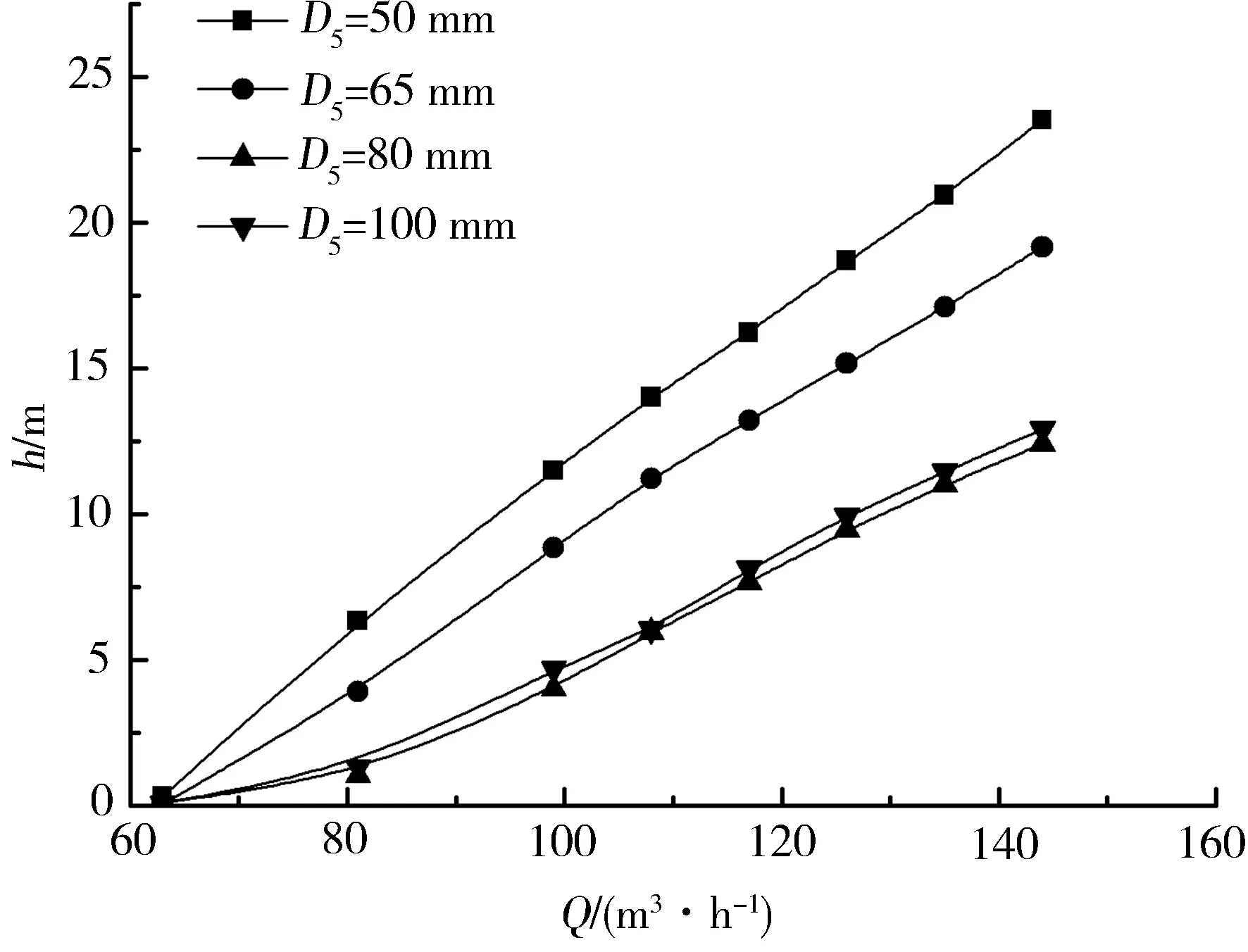
(a)蜗壳中的水力损失

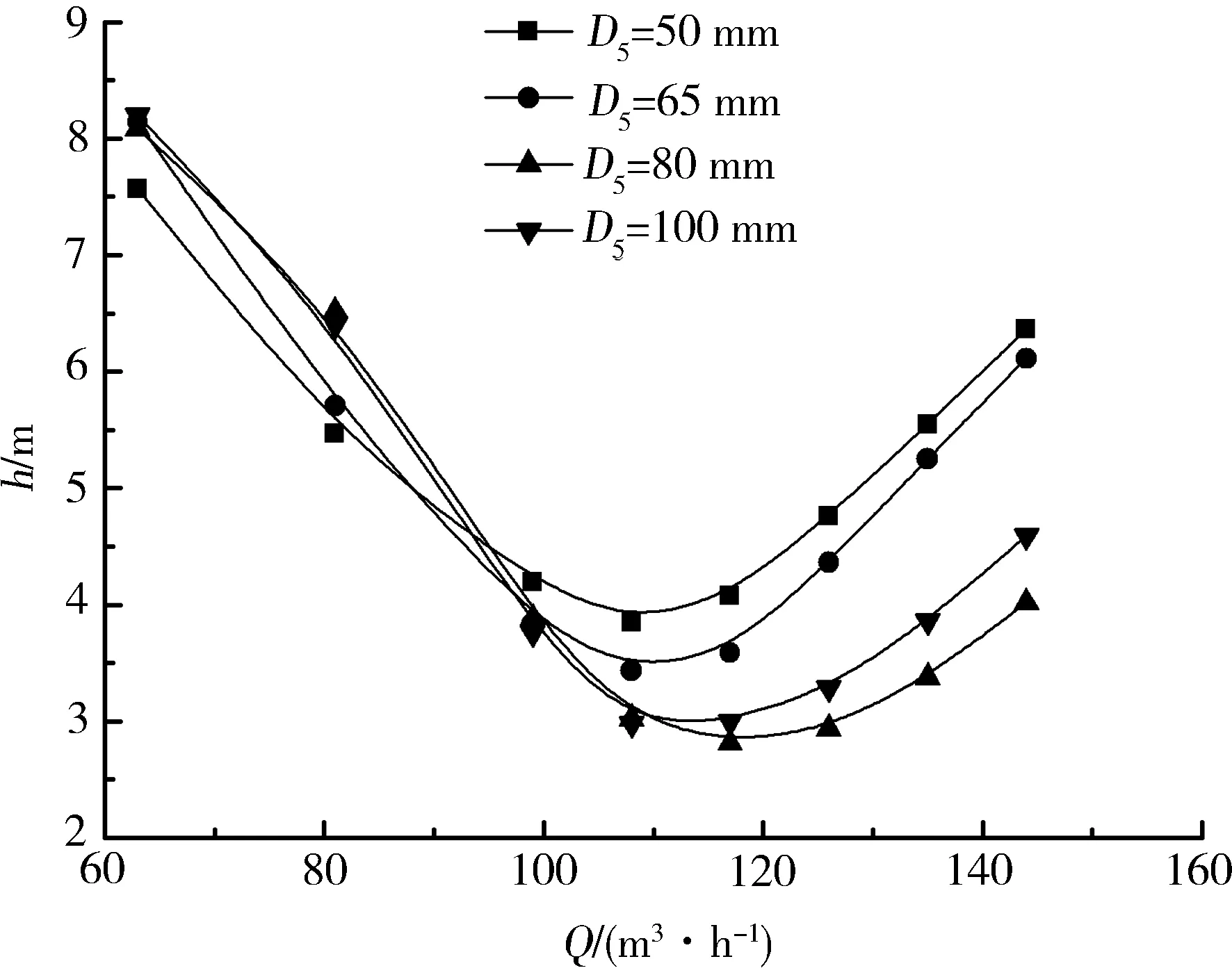
(b)叶轮中的水力损失

(c)尾水管中的水力损失

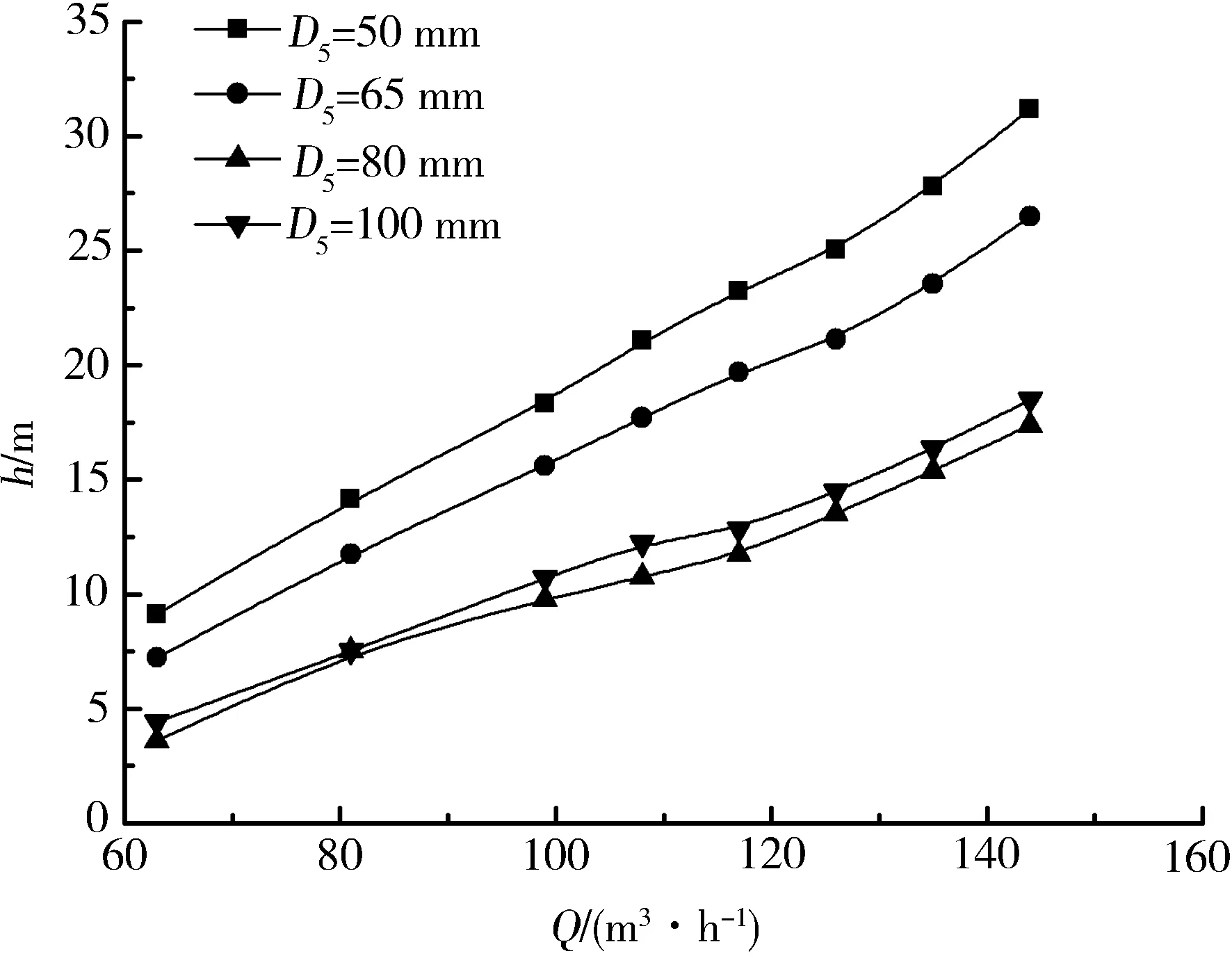
(d)总水力损失

图5 水力损失

从图5可以看出蜗壳中的水力损失和总水力损失随流量的增加而增大，叶轮中的水力损失随流量的增加先减小后增大，在小流量时小蜗壳进口下的水力损失与大蜗壳进口下的水力损失相差较小，在大流量时小蜗壳进口下的水力损失大于大蜗壳进口下的水力损失。这是因为小流量时蜗壳收缩管对流体的约束作用较弱，而在大流量下蜗壳收缩管对流体的约束作用加强，随着收缩率的逐渐增大，收缩管中的水力损失逐渐减小。在叶轮中小流量时的水力损失大于大流量下的水力损失，这是因为在小流量下叶片对流体的约束作用较弱，在叶片工作面有涡产生，且叶片背面产生脱流，导致叶轮内产生滑移；因此，叶轮中小流量时的水力损失大于大流量下的水力损失。在尾水管中除D5=80 mm时水力损失随流量的增加而减小外，其余蜗壳进口截面时尾水管中的水力损失均随流量的增加先增大后减小，且小蜗壳进口下的水力损失大于大蜗壳进口下的水力损失。

在各过流部件中，不同蜗壳进口下的水力损失除叶轮在小流量时相差较小之外其余蜗壳进口下的水力损失在小蜗壳进口下的水力损失均大于大蜗壳进口下的水力损失。表2为最高效率点时透平内部水力损失的分布。从表2可以知道在最优工况下叶轮和尾水管中的水力损失相差较小，而在蜗壳中小蜗壳进口下的水力损失均大于大蜗壳进口下的水力损失。这主要是因为随着蜗壳进口直径的增加，蜗壳收缩管的收缩率逐渐增加，收缩管中的水力损失逐渐减小。

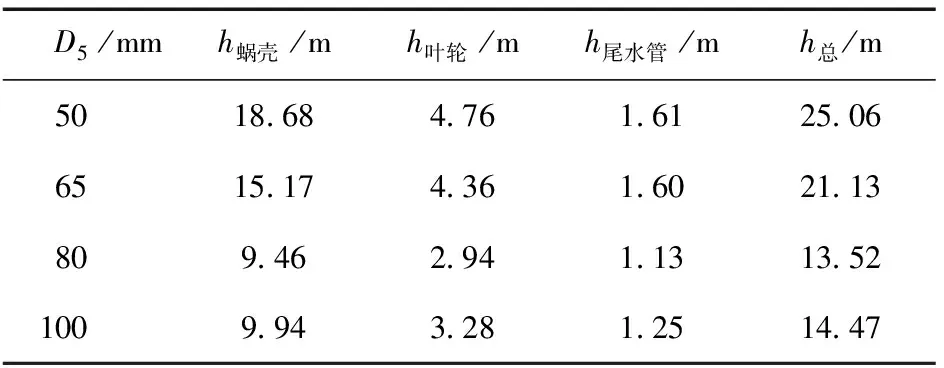
表2 最高效率点时透平内部水力损失

从图5也可以看出，在各过流部件中蜗壳中的水力损失最大，其次为叶轮中的水力损失，尾水管中的水力损失最小。蜗壳和尾水管中的损失主要是由于流体黏性的存在引起流体与壁面的摩擦损失；叶轮中的水力损失除了摩擦损失之外，还有冲击损失、分离损失、二次流损失：因此，要提高液力透平的效率对蜗壳的设计也尤为重要。

4.3 外特性

图6为不同蜗壳进口下的外特性曲线，表3为不同蜗壳进口截面时泵作透平最高效率点对应值。

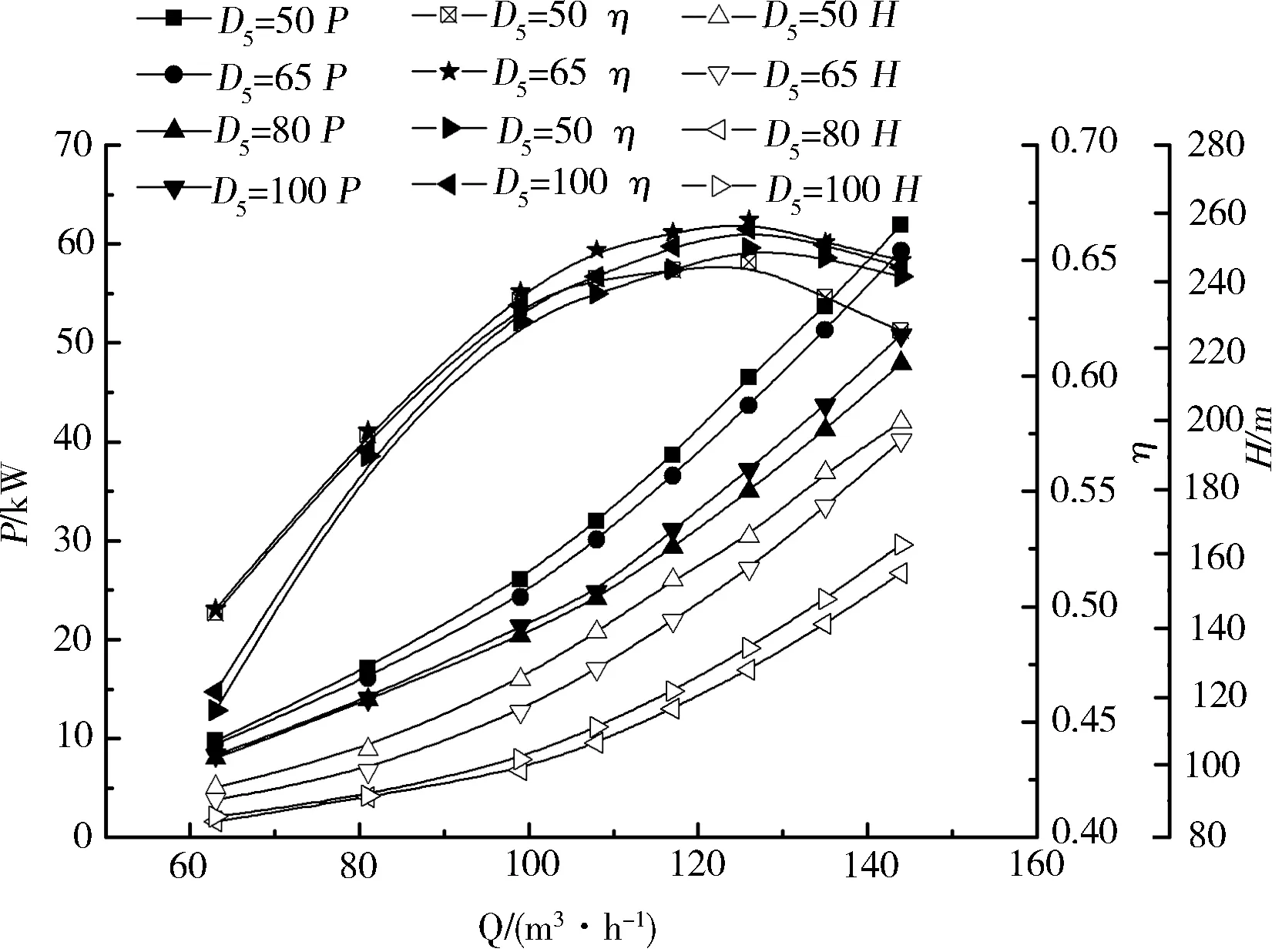
图6 外特性曲线

表3 不同蜗壳进口截面时泵作透平最高效率点对应值

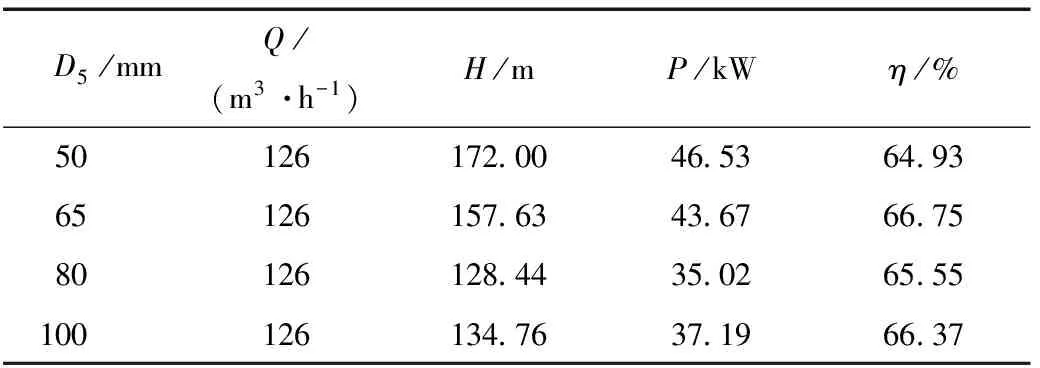
D5/mmQ/(m3·h-1)H/mP/kWη/%50126172 0046 5364 9365126157 6343 6766 7580126128 4435 0265 55100126134 7637 1966 37

从图6可以看出在不同流量下小蜗壳进口下的水头和功率均大于大蜗壳进口下的水头和功率，且在不同流量下当D5=65 mm时液力透平的效率最大。由表3可知当D5=65 mm时液力透平的效率比原设计下的效率提高了1.83%。结合以上研究结果可知，虽然当蜗壳进口直径等于65 mm时蜗壳内的水力损失较大，但在该进口下液力透平的水头却远高于原设计工况下的水头，且在该进口下所选液力透平的效率最高，叶轮进口速度矩波动最小；因此，本文所选液力透平的最佳进口直径等于65 mm。

5 结论

1)本文所选液力透平的蜗壳最佳进口直径为65 mm，比原设计下的效率提高了1.83%，且在该进口下叶轮进口的速度矩波动幅值最小。

2) 随着蜗壳进口直径的增加叶轮进口的速度矩逐渐减小；距离蜗壳收缩管较远处的速度矩随流量的增加而增大，距离蜗壳收缩管较近处的速度矩随流量的增加先减小后增大；在隔舌处，当蜗壳进口直径等于65 mm时叶轮进口的速度随流量的变化最小。

3)随着蜗壳收缩管收缩率的逐渐增大，蜗壳收缩管对流体的约束作用逐渐加强，收缩管中的水力损失逐渐减小。叶轮中小流量时的水力损失大于大流量下的水力损失。在各过流部件中蜗壳中的水力损失最大，尾水管中的水力损失最小。

[1] 张克危. 流体机械原理[M]. 北京：机械工业出版社，2000：76-92.

[2] 杨华, 刘超, 汤方平, 等. 不同叶片包角的离心泵试验与数值模拟[J]. 机械工程学报, 2007, 43(10):166-169.

[3] 何有世, 袁寿其, 郭晓梅, 等. 带分流叶片的离心泵叶轮内三维不可压湍流场的数值模拟[J]. 机械工程学报, 2005, 40(11):153-157.

[4] 郎大鹏, 杨爱玲, 徐洋, 等. 叶片出口角对离心泵流动诱导噪声的影响研究[J]. 工程热物理学报, 2014(1)：15.

[5] 钱忠东, 张凯, 王志远. 双吸式离心泵叶片头部形状对泥沙磨损的影响[J]. 排灌机械工程学报, 2014, 32(2):103-107.

[6] 牟介刚,施瀚星,郑水华,等.蜗壳断面形状对泵径向力平衡影响的研究与探讨[J].水泵技术，2013(3):7-10.

[7] 杨孙圣,孔繁余,薛玲,等.长短叶片对液力透平性能的影响[J].农业机械学报，2012,43(7):104-107.

[8] DERAKHSHAN S, MOHAMMADI B, NOURBAKHSH A. Efficiency improvement of centrifugal reverse pumps[J]. Journal of Fluids Engineering, 2009, 131(2):021103.

[9] YANG S S, KONG F Y, CHEN H, et al. Effects of blade wrap angle influencing a pump as turbine[J]. Journal of Fluids Engineering, 2012, 134(6):061102.

[10] 杨孙圣.离心泵作透平的理论分析数值计算与实验研究[D]. 镇江：江苏大学，2012.

[11] DERAKHSHAN S, NOURBAKHSH A. Theoretical, numerical and experimental investigation of centrifugal pumps in reverse operation[J]. Experimental Thermal and Fluid Science, 2008, 32(8):1620-1627.

[12] 王桃，孔繁余，何玉洋,等.离心泵作透平的研究现状[J].排灌机械工程学报，2013，31(8):674-680.

[13] 关醒凡.现代泵理论与设计[M].北京：中国宇航出版社，2011：303-313.

[14] 王立文, 高殿荣, 吴建伟. 无阀微泵扩散管及收缩管流动特性分析[J]. 机床与液压, 2006 (6):159-162.

[15] 李俊,沈雪明,应济,等.基于MEMS的扩张管/收缩管内流动特性分析[J].机床与液压，2008,36(12):61-63.

[16] 杨军虎，龚朝晖，夏书强，等. 导叶对液力透平性能影响的数值分析[J]. 排灌机械工程学报,2014,32(2):113-118.

(编校：夏书林)

EffectofEntranceSectionofHydraulicTurbineonHydraulicLossandVelocityTorque

SHI Guang-tai,YANG Jun-hu*

(CollegeofEnergyandPowerEngineering,LanzhouUniversityofTech.，Lanzhou730050China)

The diffusion tube of volute outlet becomes the shrinkable tube of hydraulic turbine when centrifugal pump acts as hydraulic turbine. The energy loss between the diffusion tube and shrinkable tube is different, as well as the effect of the shrinkable tube of different shrinkage rate on hydraulic loss and velocity torque of hydraulic turbine. In order to reduce hydraulic loss of each the flow components in hydraulic turbine and improve the efficiency of hydraulic turbine, the base circle of volute of a single stage hydraulic turbine is regarded as a loop line under the different entrance section. The tangential velocity along the loop line is calculated. Correspondingly, the velocity torque is work out with the radius of base circle. Four monitoring points in the loop are set up. At the points, the velocity torque varies with the flow rate. The varieties are analyzed with ANSYS software and effect of the entrance section of volute on hydraulic loss of each the flow components is studied. The results show that the optimum entrance diameter of volute of hydraulic turbine is equal to 65 mm. Compared to the original design, the efficiency of improved hydraulic turbine increases by 1.83%. Fluctuant amplitude of velocity torque of impeller entrance is minimum in the volute entrance. With increasing volute entrance diameter, velocity torque of impeller entrance and the hydraulic loss is gradually decreased. Meanwhile the shrinkage rate of shrinkable tube in volute gradually increases.

hydraulic turbine; volute; hydraulic loss; velocity torque

2014-04-28

国家自然科学基金(51169010)；“十二五”国家科技支撑计划资助项目(2012BAA08B05)；甘肃省教育厅导师基金(0278)。

史广泰(1985—)，男，博士研究生，主要研究方向为流体机械内部流动规律。E-mail:shiguangtai_1985@126.com。

*通信作者：杨军虎(1962—)，男，教授，博士生导师，主要研究方向为流体机械内部流动机制及设计理论。E-mail:lzyangjh@lut.cn。

TH322

：A

：1673-159X(2015)01-0084-06

10.3969/j.issn.1673-159X.2015.01.015