完全图哈密尔顿圈遗传算法的MATLAB模拟实现

刘奕君, 张 立2, 赵 强

(1.徐州医学院医学信息学院，江苏 徐州 221000；2.徐州医学院医学影像学院，江苏 徐州 221000)

· 计算机软件理论、技术与应用·

完全图哈密尔顿圈遗传算法的MATLAB模拟实现

刘奕君1, 张 立2, 赵 强1

(1.徐州医学院医学信息学院，江苏 徐州 221000；2.徐州医学院医学影像学院，江苏 徐州 221000)

求解完全图上的哈密尔顿圈是典型的组合优化问题，遗传算法是解决此类NP问题的一种较理想的方法。对基本的遗传算法进行改进，在选择操作和变异操作中加入贪心优化思想，使算法获得更优的全局最优解。在MATLAB环境下模拟实现了哈密尔顿圈的经典问题——TSP( travelling salesman problem)旅行商问题，从而验证了该算法的可行性和正确性。

哈密尔顿圈；遗传算法；贪心思想；MATLAB；全局最优解

设G(V，E)是一个连通图，若G中一条回路通过G的每个点恰好1次，这样的回路称为哈密尔顿回路，记作H回路。对于H回路问题，传统的穷举搜索法、贪心法、动态规划法等串行算法，都面临着所谓“组合爆炸”问题[1]。对于这类NP(non-deterministic polynomial)问题，可用并行求解法或演化算法等。演化算法[2-3]是用计算机模拟大自然的演化过程，特别是生物进化过程，以求解复杂问题的一类计算模型，其基本思想是Darwin的进化论和Mendel的遗传学说。该类算法可通过逐步的演化过程，使群体进化到包含或接近最优解的状态。遗传算法即典型的演化算法[4]，提供了一种求解复杂系统优化问题的通用框架，不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，所以广泛应用于很多学科[5-8]。

TSP(travelling salesman problem)问题的数学模型便是带权的H回路问题，即对n个城市,要找一条走遍每个城市一次且仅一次的最短闭合路径。其实际模型在路径、网络、分配等优化问题中有着广泛的应用。用于求解 TSP 的现代优化算法主要包括模拟退火算法、人工免疫算法、蚁群算法、禁忌搜索算法、 神经网络算法等[9]。它们存在着全局搜索能力差的弱点，极有可能找到的是局部最优解[10]。本文采用的遗传算法，具有较好的全局搜索性能，是目前解决TSP问题的较为有效的方法。

1 针对哈密尔顿圈问题的遗传算法设计

1.1 算法分析与设计

遗传算法的基本流程如图1所示，包括3个基本操作：选择、交叉和变异。选择(selection)是用来确定重组或交叉个体，以及被选个体将产生多少个子代个体。首先计算适应度，然后按照适应度进行父代个体的选择。基因重组是结合来自父代交配种群的信息产生新的个体。交叉之后子代经历的变异，实际上是子代基因按小概率扰动产生的变化。

图1 遗传算法的基本流程

遗传算法的染色体编码方案，通常有二进制编码和浮点数编码2种，而对于求哈密尔顿圈的问题，浮点数编码更适合。例如，染色体(1，2，3，4，5)即表示该哈密尔顿圈由1点出发，经过点2-5又回到1点。回路长度是度量某个染色体的优良性的标准，长度越小，说明染色体越优秀，应该保留，这也是本算法中适用度函数的考量点。

在初步实现时，发现基本的轮转法和变异算法在获得全局最优解时，性能较差，很难在随机的自然选择中得到和保留最优的种群基因，故本文将贪心的思想加入这2个步骤中。这种贪心思想是最优保存方法的体现。遗传算法的理论已经证明了轮转法选择算子不能收敛到全局最优解，而最优保存方法[11]能收敛到全局最优解。在选择种群时，每次用最好的种群基因将最差的一部分基因替换掉，再用轮转法选择，在变异时，将变异概率增大，使得上一次的优秀基因有更多的变异机会，这样可以在一定程度上解决因贪心选择造成的种群多样性减少的问题。同时，在变异时，同样加入贪心的思想，只有当变异后的基因优于原基因时，才使此次变异成功，否则失败。这样又能使整体算法的收敛速度加快，也更易获得全局最优解。在交叉操作中，选择文献[10]的顺序交叉操作方法，因为这种交叉方法更适合于哈密尔顿圈的特性。

1.2 算法描述

步骤1 编码初始化。设置最大进化代数MaxG，种群规模N，贪心替换算子Pr，变异算子Pm和交叉算子Pc，并生成初始随机种群。

步骤2 个体评价。用适应度函数对每个基因进行评价。

步骤3 选择操作。首先用最优的染色体方案替换占种群规模Pr的最坏个体，再用基本轮转法进行选择。

步骤4 交叉操作。采用顺序交叉操作方法。

步骤5 变异操作。只有当变异后的基因优于原基因时，变异成功。

步骤6 终止条件。当进化代数大于MaxG时，算法结束，否则转向步骤2。

2 MATLAB编码实现

本文的MATLAB仿真并没有采用已有的遗传算法工具包，而是根据设计的算法进行了重新编写，特别是选择和变异操作。选择操作中的贪心思想代码如图2所示，变异操作中的贪心思想代码如图3所示。

图2 选择操作中的贪心思想代码

图3 变异操作中的贪心思想代码

3 算法验证与试验分析

3.1 算法验证

本文采用经典的Oliver 30城市问题[12]进行算法验证。当最大进化代数MaxG取400，种群规模N取600，贪心替换算子Pr取0.25，变异算子Pm取0.12和交叉算子Pc取0.3时，经过数次运行，得到的最优路径，如图4所示。比传统的二叉树描述法的结果428.90和启发式搜索法的结果436.01[13]都有更高的性能，且速度更快。图5示出某次运行得到的最优解随进化代数的趋势。

图6示出的是再随机生成200个城市的坐标(X，Y坐标的范围在[0,800])，经过数次运行后，得到的最优解。

图4 30城市问题求解的最优路径

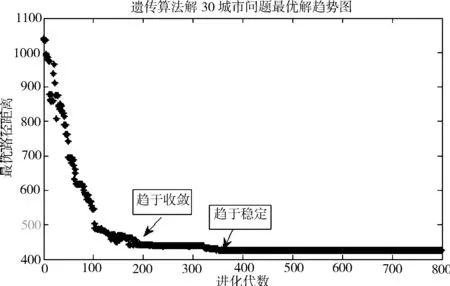
图5 30城市问题求解的最优解随进化代数的趋势图

图6 随机产生的200城市问题求得的最优路径

3.2 实验分析

从图4和图6可以看到，求得的路径均没有产生交叉的线路，表明该算法求解是有效的。另外，从图5可以看到，当进化到第1个做标记的代数时，算法开始趋于收敛，同时又存在很小的波动，且这些波动是趋向于更好的染色体形态，这是在变异时加入了贪心思想的原因。图5的收敛种群代数约为200代，较文献[12]的收敛速度慢，这是因为在选择操作时的贪心替换，使得种群的多样性下降，有更多的进化代数便是这种选择要付出的代价；因此，在交叉和变异算子的选择时，应适当增大相应的取值，以增加种群的个体多样性，从而获得全局最优解。

4 结束语

本文对基本的遗传算法进行了改进，在进行选择操作时，将最优值替换和轮转法相结合，使算法更容易获得全局最优解，同时，在变异操作中采用取优值的贪心方法，以获得更优秀的变异个体。本文的后继工作主要考虑：如何使算法整体的收敛速度得到提升；在交叉操作时，如何提升贪心的效率。

[1]方俊,潘勇.哈密顿回路问题的DNA表面计算模型[J].计算机工程与应用，2006，42(30):62-64.

[2]李悦乔,康立山,李程俊.求解TSP问题的实数编码演化算法[J].计算机工程与设计,2007(19):14-16.

[3]蔡之华,彭锦国,高伟，等.一种改进的求解TSP问题的演化算法[J].计算机学报,2005(5):74-79.

[4]刘勇，刘宝坤，李光泉.基于MATLAB平台的遗传算法工具包[J].天津大学学报：自然科学版,，2001(4):490-494.

[5]Mat Buckland.游戏中的人工智能技术[M]. 吴祖增，沙鹰，译.北京：清华大学出版社， 2006：723-764.

[6]王小平，曹立明.遗传算法：理论、应用与软件实现[M].西安：西安交通大学出版社，2002:300-400.

[7]张文修，梁怡.遗传算法的数学基础[M]. 西安：西安交通大学出版社， 2000：500-560.

[8]周明，孙树栋.遗传算法原理及应用[M]. 北京：国防工业出版社， 1999：120-200.

[9]周康,强小利,同小军，等.求解TSP算法[J].计算机工程与应用,2007, 43(29):43-47.

[10]高友智.基本遗传算法及其改进[J].武汉化工学院学报，2003(2):77-78.

[11]谢胜利，张燕姑，李广.基于遗传算法的旅游商问题求解[J].温州师范学院学报：自然科学版，2002，22(3)7-10.

[12]曲中水，刘淑兰.基本遗传算法的收敛性分析方法[J].哈尔滨理工大学学报，2003(1):45-48.

[13]刘振,胡云安.一种多粒度模式蚁群算法及其在路径规划中的应用[J].中南大学学报：自然科学版,2013(9):150-159.

(编校：饶莉)

TheSimulationofGeneticAlgorithmforHamiltonCircleonCompleteGraphinMATLABEnvironment

LIU Yi-jun1, ZHANG Li2, ZHAO Qiang1

(1.SchoolofMedicineInformation，XuzhouMedicalCollege，Xuzhou221000China;2.SchoolofMedicalImaging，XuzhouMedicalCollege，Xuzhou221000China)

Solving Hamilton-circle on a complete graph is a typical combinatorial optimization problem. Genetic algorithm is a good way to solve such an NP problem. In this paper, the basic genetic algorithm is improved. Particularly, the greedy optimization ideas are applied to the selection and mutation operation in order to obtain global optimal solutions with the algorithm. In the MATLAB environment, the algorithm was simulated to implement classical Hamilton circle- TSP (travelling salesman problem) and the results verify the feasibility and correctness of the algorithm.

Hamilton-circle; genetic algorithm; greedy thoughts; MATLAB; global optimal solutions

2014-03-13

徐州市科技计划项目(XM13B021)；徐州市科技计划项目(XM12B077)。

刘奕君(1983—)，女，讲师，主要研究方向为计算机软件设计、信号处理。

TP311; TP312

：A

：1673-159X(2015)04-0013-04

10.3969/j.issn.1673-159X.2015.04.003