固体火箭发动机试车架中板簧弹阻力有限元计算方法

张龙飞，胡全星

（中国航天科技集团公司第四研究院四○一所，陕西西安710025）

固体火箭发动机试车架中板簧弹阻力有限元计算方法

张龙飞，胡全星

（中国航天科技集团公司第四研究院四○一所，陕西西安710025）

以固体火箭发动机试车架中重要的零部件板簧为研究对象，为了实现对多段板簧弹阻力的分析计算统一处理，编写Matlab-m有限元计算程序对试验过程中板簧的变形产生的弹阻力Q进行分析计算，计算考虑了由轴向力引起的几何刚度矩阵，得到了弹阻力Q与位移Δ的解析关系，进而可以确定板簧的最佳工作点。设计的算法、计算思路和结果为下一步进行板簧设计、结构优化、失稳分析等提供一定的参考作用。

板簧；Matlab；有限元；刚度矩阵

固体火箭发动机试车架是地面点火试验的主要设备，其动架和定架之间靠板簧连接，可使整个结构动态响应好，对测力传感器校定影响小，提供沿发动机轴向运动的小位移自由度，使发动机推力全部作用到推力传感器上。但板簧是弹性体，在推力测量过程中会产生阻力，所以有必要对板簧弹阻力进行计算与估计。对此，王德厚等［1］基于力学的基本理论建立微分方程组计算得到了单工作段板簧弹阻力的理论解；文献［2］建立了双工作段板簧的有限元模型，通过ANSYS分析得到了具体弹阻力值的大小。为了实现对多段板簧进行更精确的结构分析，计算弹阻力的解析表达式至关重要，建立微分方程的方法过于复杂，计算过程容易出错；采用有限元分析软件（如ANSYS等）只能输入具体参数值得到数值结果。

笔者建立了3种结构形式板簧的有限元模型，基于有限元的基本理论，通过在Matlab中编写m文件程序的方法对单段到多段板簧弹阻力的计算实现了统一处理，均可以得到含有板簧几何参数变量的解析表达式［3］。首先应用单段板簧的计算结果和航天标准中的理论解进行对比，用以验证算法的有效性。随后分别给定单段到三段板簧的具体参数进行算例计算，并对3种板簧的弹阻力变化进行对比分析。基于本文的计算结果，通过结构优化可以设计板簧合适的工作点，保证结构稳定的条件下提供最小的弹阻力，在试验中测试到更加精确的推力值。

1 板簧有限元模型

1.1 有限单元法静力分析理论

结构静力分析的平衡方程可以表示为

式中：K为刚度矩阵；δ为位移向量；R为载荷向量。

如果为梁单元，考虑轴向力时，则应包含几何刚度矩阵，即

对于由一系列单元组成的结构，整体刚度矩阵（K+Kg）将总体坐标的结点位移δ和整个结构的总体载荷R联系在一起，总体刚度K、Kg分别是由单元刚度矩阵ke和几何单元刚度矩阵kg经过总装而成［4］。

1.2 板簧结构以及单元划分

板簧作为固体火箭发动机试车架中动架和静架的连接构件，具有重复性好、弹阻力小和结构简单的优点，广泛应用在各种试车架中［5］。板簧的结构形式如图1所示。

在图1中，进行了单元以及几何参数的标记，①～⑤表示单元号。三工作段板簧（或多段）为新提出的板簧形态，相比于单段和双段板簧，具有可修改参数多，在大吨位高精度试车架中，提高侧向刚度的同时，为设计弹阻力值及其变化提供更多的选择范围。

结点单元划分如下：

1）单工作段板簧2个结点1个单元。

2）双工作段板簧4个结点3个单元。

3）三工作段板簧6个结点5个单元。

1.3 板簧几何模型简化

运用Matlab对板簧进行分析计算前，需建立其简化模型［6］。为了保证计算的准确性，建立板簧简化模型采取以下规则：

1）板簧与动架、静架的连接采用刚体焊接结构，分析中认为焊接质量可靠，不考虑焊缝对传力效果的影响，把板簧当作连续体来处理。

2）删除板簧一些微小特征，如螺栓连接的螺孔、螺纹等。其对计算结果产生的影响可以忽略，完全能保证结果精确度。

3）应对板簧受到的载荷进行合理的分配，使其作用在适当的位置。

笔者简化板簧为梁模型，假设为二维梁单元，结点具有3个自由度（轴向位移u，横向位移v，转角θ），根据板簧实际的安装状态，其约束设置为：

下端结点固定（u1=0，v1=0，θ1=0）；上端结点转角约束（θ顶端=0）。

笔者分析所用到的各变量定义如表1所示。

表1 板簧分析中所用到的符号

1.4 板簧受力分析及提出问题

板簧的受力如下图2所示。

当板簧一端相对另一端产生一个位移Δ时，计算引起位移弹阻力Q的大小，分析Q随着板簧的轴向压力P的变化趋势，进而确定板簧合适的工作状态。通过编写程序，实现对单段到多段板簧的统一计算，可得到含有板簧几何参数变量的弹阻力Q的解析表达式。

2 计算结果及其验证

2.1 计算结果

Matlab软件已成为当今工业设计计算的主要工具，主要特点是计算元素为矩阵，在处理参数多、计算量大的问题时快速而精确［7］。程序结构为建立3个函数。

1）主函数：该函数主要负责变量、结点、单元的定义，原始数据的输入、函数的调用、结果的输出。

2）单元刚度矩阵计算子函数：该函数主要负责接收相关变量，返回值为单元刚度矩阵和单元几何刚度矩阵。

3）单元刚度矩阵组装子函数：该函数主要是接收相关变量，返回值为单元刚度矩阵组装的参数值。

几何单元刚度矩阵和单元刚度矩阵［8］分别具有以下组成形式：

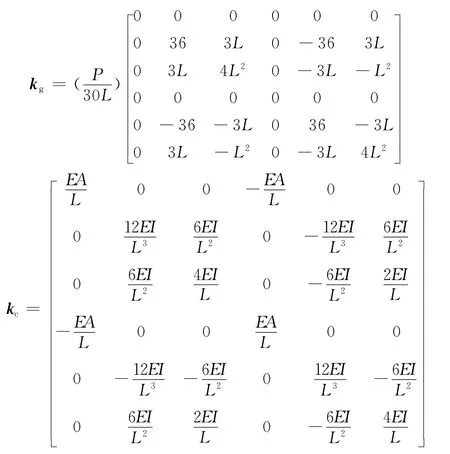
运行程序分别对单段、双段以及三段板簧进行计算，得到含有板簧结构几何尺寸、轴向力、横向力的表达式如下：

式中：P1=25b3E3h16h23；P2=18l3P3r2（3l+2r）+ 10b2E2h13P［3h13r2+h23l（13l+15r）］；P3= 3bEl P2［15h23l2（l+4r）+2h13r2（26l+5r）］；Q1= 3l3P2r2（32l2+39lr+12r2）；Q2=25b2E2h13［h13r3+ 2h23l（4l2+6lr+3r2）］；Q3=10bEl P［h13r2（24l2+ 19lr+3r2）+2h23l2（4l2+18lr+9r2）］

3）三工作段板簧

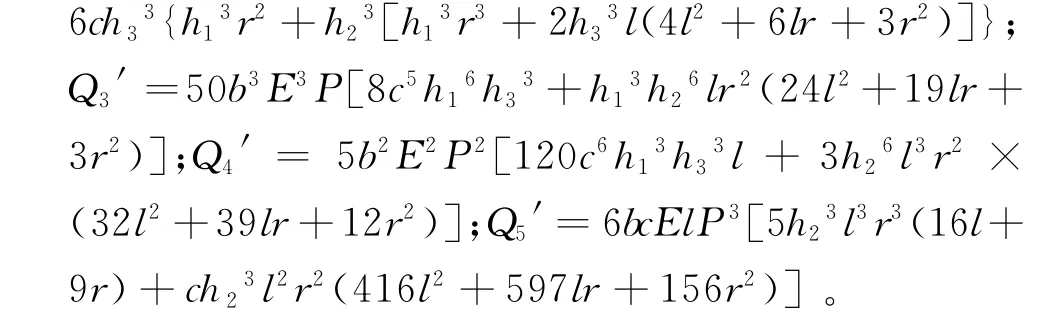
2.2 算法正确性验证

由于程序对多段板簧的计算统一处理，所以只需要对单段进行验证即可。航天标准通过建立板簧的梁模型，基于力学的基本理论得到板簧挠曲线的微分方程，通过计算给出单工作段板簧的弹阻力Q的理论解如下所示：

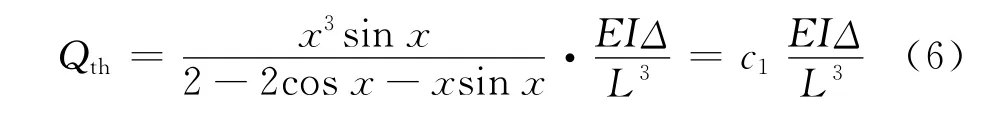
对有限元的计算解式（3）进行变量替换得：

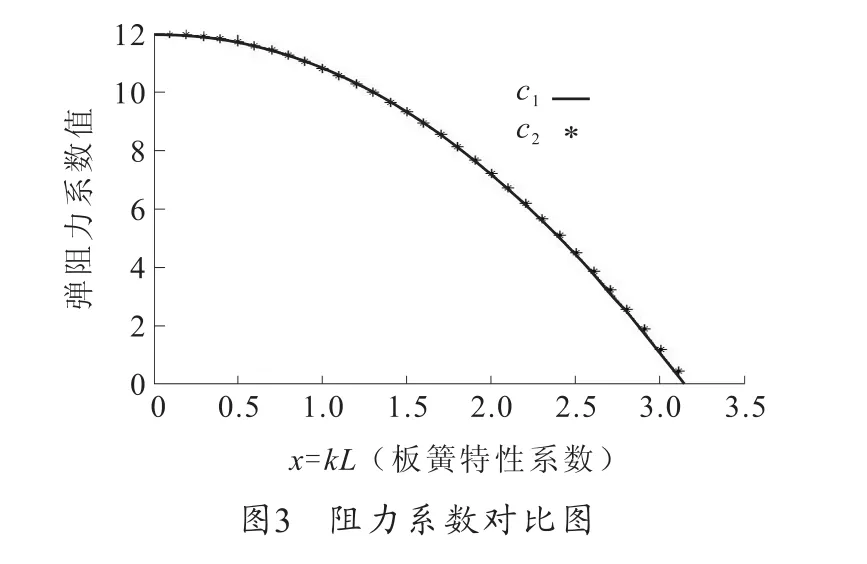
对比式（6）、（7）可以看出，只要两个式子前部分系数c1、c2相等，就可以说明式（3）计算的结果是正确的。

从图3可以看出，两个系数值基本吻合，在多段板簧的计算中，由于程序计算是重复迭代进行的，至此可以验证所编写程序的正确性。

3 算例

板簧的材料选用弹簧钢，弹性模量E= 206 GPa。

1）单工作段板簧

参数取值为：L=240 mm；b=100 mm；h= 4.5 mm。

弹阻力Q的计算结果为

当P=13 800.85 N，Δ≤0.5 mm时，Q≤33.39 N。

2）双工作段板簧

参数取值为：L=240 mm；l=24 mm；r= 192 mm；b=100 mm；h1=2.85 mm；h2=15 mm。

弹阻力Q的计算结果为

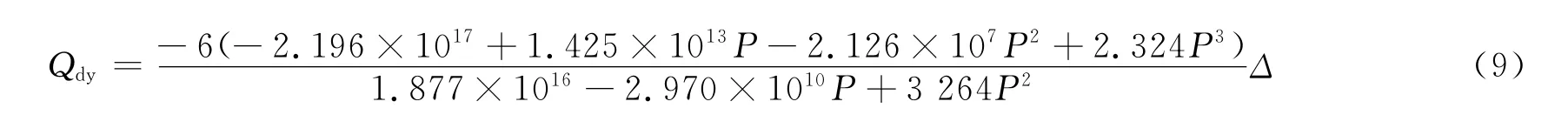
当P=13 800.85 N，Δ≤0.5 mm时，Q≤4.41 N。

3）三工作段板簧

参数取值为：L=240 mm；l=18 mm；c=12 mm；r=180 mm；h1=2.85 mm；h2=5 mm；h3=15 mm；b=100 mm。

弹阻力Q的计算结果为

当P=13 800.85 N，Δ≤0.5 mm时，Q≤10.27 N。

4 结果分析

从弹阻力表达式可以看出，无论是单段、双段还是多段板簧，当轴向压力P固定不变时，弹阻力Q均和位移Δ成比例关系。在试验过程中，为了提高测试精度，有必要进一步分析Q的变化趋势以及确定板簧的最佳工作点，根据Q的表达式，就可以得到当Δ固定不变时弹阻力Q的系数随着P的变化趋势，分别绘制其趋势如图4所示。

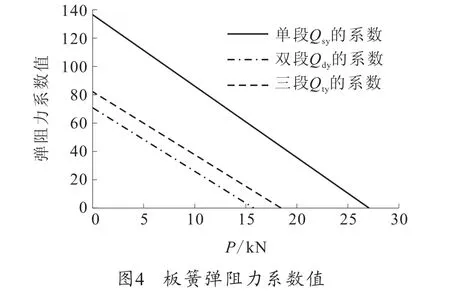
从图4可以看出，无论是单段、双段还是三段板簧，弹阻力的系数值随着压力P是呈直线减小的关系。针对算例中板簧几何参数的取值，计算斜率得ksy=－0.005，kdy=－0.004 44，kty=－0.004 40，即弹阻力随着压力P的衰减率是相当的，对于确定的压力P，Qsy＞Qty＞Qdy。对于目前广泛使用的双段板簧，更改参数l、r（板簧的总长2l+r=240 mm不变），l、r分别取以下3种模型：

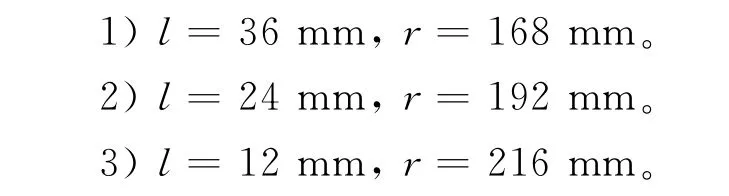
得到弹阻力Q随着压力P变化如图5所示。可以看出，从模型1到3，l长度减小，r长度增加，弹阻力的值呈增大的趋势，并随着压力P的变化，弹阻力的下降速率相当。

从图3可以看出单工作段板簧在kL≤1.0的一段，弹阻力变化平稳，最有利于用在带原位校准装置的试车架中，这时因初始弹阻力已在原位校准中被消除，由弹阻力带来的误差主要是因发动机在工作过程中质量逐渐减小所引起的弹阻力变化量所决定的。工作点选在这一段中，保证了弹阻力变化量和推力测量误差最小。

当板簧受压力时，P达到临界载荷Pcr时，弹阻力Q=0，亦即达到板簧的失稳状态，从Q直线变化的趋势可以得到，在发动机试验过程中，对于特定的发动机质量（压力P），选定或者设计板簧的时候，在保证板簧不被破坏的基础上选接近压板簧Q=0的点为工作点，此时的弹阻力基本上接近于零，用在不带原位校准装置的试车架中可减小推力测量误差。

从算例计算中可以看出，当板簧的位移Δ≤0.5 mm时，弹阻力Q值很小，这样数量级的弹阻力大小相比于发动机的推力值属于可以接受的范围。

5 结论

1）建立了3种结构形式板簧的有限元模型，通过在Matlab中编写m文件程序计算得到弹阻力Q与位移Δ的表达式。对板簧的静力分析、失稳分析等可以提供更精确的数学模型。

2）本设计程序具有通用性，将求解多段板簧的弹阻力与位移的关系统一处理。在将来板簧的设计计算中，对于不同规格的发动机选择的多段板簧，只需要设置初始的输入参数，不用对程序进行更改，就可以方便地进行计算。

3）板簧的弹阻力跟位移成比例关系，随着压力的增大呈减小趋势。对于特定的板簧一般选取接近失稳的点为工作点，此时弹阻力最小。

（Referenees）

［1］王德厚.单板簧的设计计算［R］.西安：航天动力技术研究院，1997.WANG Dehou.The design and calculation of the single plate spring［R］.Xi'an：The Research Institute of Space Power Technology，1997.（in Chinese）

［2］潘娜.固体火箭发动机试车架结构有限元分析［D］.西安：航天动力技术研究院，2008.PAN Na.The finite element analysis of test frame structure in SRM［D］.Xi'an：The Research Institute of Space Power Technology，2008.（in Chinese）

［3］ROQUE C.Symbolic and numerical analysis of plates in bending using Matlab［J］.Joural of Symbolic Computation，2014，61：3- 11.

［4］RAH MAN T，VALDMAN J.Fast MATLAB assembly of FEM matrices in 2D and 3D：nodal elements［J］.Applied Mathematics and Computation，2013，219（13）：7151- 7158.

［5］薛群，徐向东.固体火箭发动机测试与试验技术［M］.北京：中国宇航出版社，1994.XUE Qun，XU Xiangdong.The test technology of solid rocket motor［M］.Beijing：China Aerospace Press，1994.（in Chinese）

［6］李海涛.火箭发动机推力矢量测量理论、方法与自动测试技术研究［D］.长沙：国防科学技术大学，2005.LI Haitao.Research on the theory＆method of trust vector measurement and the automatic test technology in rocket engine ground test［D］.Changsha：National University of Defense Technology，2005.（in Chinese）

［7］ZANDER N，BOG T，ELHADDAD M，et al.A finite cell research toolbox for MATLAB［J］.Advances in Engineering Software，2014，74：49- 63.

［8］LOGAN D.A first course in the finite element method［M］.Beijing：Publishing House of Electronics Industry，2003.

The Finite Element Method for Caleulating Elastie Resistanee of Plate Spring in SRM Test Frame

ZH ANG Longfei，HU Quanxing
（The 401st Institute of the Fourth Institute of CASC，Xi'an 710025，Shaanxi，China）

plate spring；Matlab；finite element；stiffness matrix

V416.1

A

1673-6524（2015）04-0050-05

2015- 01- 13；

2015- 04- 09

张龙飞（1988－），男，硕士研究生，主要从事固体火箭发动机试验测试研究。E-mail：704771327＠qq.com

Abstraet：The important parts（plate spring）in SRM test frame are taken as the research object.For the purpose of achieving a unified treatment in analysis and calculation of elastic resistance of multistage plate spring，the Matlab-m finite element calculation program is to be made for the analysis and calculation of elastic resistance Q produced from the deformation of the plate spring in the process of testing，which takes the geometric stiffness matrix of axial force into account.The analytical relationship of resistance Q and displacementΔis obtained，which makes it possible to pinpoint the optimal working point of plate spring.The designed algorithm，train of thought and results of calculation are preparations for plate spring design，structure optimization，and buckling analysis，etc.