Resource Allocation Algorithm Based on PSO-GA for Multi-User OFDM System

Hao-Ye Zhang, Jin-Ping Mei, and Shi-Bing Zhang

1. Introduction

With the development of communication service, the demanding on the quality of communication becomes growing, which constantly promotes the emerging of advanced communication technologies. Orthogonal frequency division multiplexing (OFDM) is widely used in various communication systems due to the outstanding anti-multipath interference ability and higher spectral efficiency[1].

In the OFDM system, the resource allocation would affect the performance a lot. A reasonable allocation of sub-carriers and bits would effectively reduce transmitted power and bit error rate of a system. The water-filling method is commonly used to optimize the allocation of sub-carriers and bits in the single-user OFDM system[2].But the allocation of sub-carriers and bits in a multi-user OFDM system is more complex.

There are two kinds of the resource allocations in a multi-user system, that is, static allocations and dynamic allocations. The static allocations, such as OFDM with time division multiple access (OFDM-TDMA) and OFDM with frequency division multiple access (OFDM-FDMA), do not take the channel state information (CSI) into consideration.Therefore, some serious faded sub-carriers will be discarded, which results in the reduction of spectral efficiency and decrease of system throughput. In fact, the channel gains of each sub-carrier in OFDM will change with different users. A well sub-carrier to one user may be unsuitable for another; vice versa, a serious faded sub-carrier to one user may be suitable for another user.Therefore, dynamic allocations are more practical to the multi-user OFDM system.

The optimal sub-carrier, bit, and power allocation algorithm was proposed based on Lagrange multipliers in[3]. But this algorithm is too complex and only has the optimal solution in theory. Some suboptimum algorithm,such as greedy algorithm put forward in [4] and [5],balances the complexity and user rate fairness. Zhang proposed an iterative water-filling algorithm to solve problems on the sub-carrier allocation to minimize the total transmitted power of system[6]. The margin adaptive algorithm (MA) and rate adaptive algorithm (RA) were used in down link of the multi-user OFDM system in [7],and the distributed practical resource allocation algorithm was presented in [8] and [9]. Furthermore, genetic algorithm (GA) is also used to minimize the total transmitted power[10]or maximize the total throughout[11].

GA has the advantages of effective nonlinear programming and scheduling search capacity. But it is very sensitive to the selection of initial population, and the convergence is slow[12]. Besides, the particle swarm optimization (PSO)[13]has good robustness of initial population and fast rate of convergence at the initial phase of algorithm. But when the PSO algorithm approaches to the globally optimal solution, it has relatively slow search speed and it is easy to fall into local optimum. The performance of PSO algorithm is inferior to that of GA when there are comparatively more sub-carriers.

In this paper, we address the resource allocation algorithm in the multi-user OFDM system and propose an improved algorithm to minimize the total transmitted power of system. The improved algorithm combines the particle swarm optimization algorithm with genetic algorithm(PSO-GA) and it is used to allocate optimally the sub-carriers and bits of the multi-user OFDM system.

The rest of this paper is organized as follows. In Section 2, the system model is provided. Then the improved PSO-GA algorithm is described in Section 3.Simulation results are shown in Section 4. Finally, some conclusions are drawn in Section 5.

2. System Model

Suppose that there are K sub-carriers and N users in the multi-user OFDM system, and the nth user should transmit Rnbit data. The received power required to transmit rk,nbit data on the kth sub-carrier by the nth user is given by

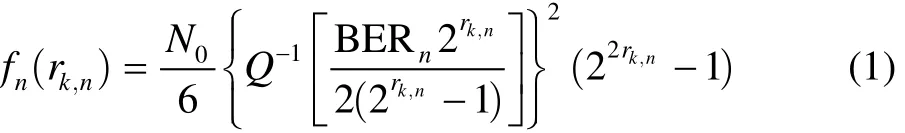
where N0is the additive noise power spectral density of the system, and BERnis the error rate of the nth user. Then, the transmitted power required by the nth user on the kth sub-carrier is equal to

where Gk,nis the channel gain of the nth user on the kth sub-carrier. Therefore, the total transmitted power of multi-user OFDM system is given as

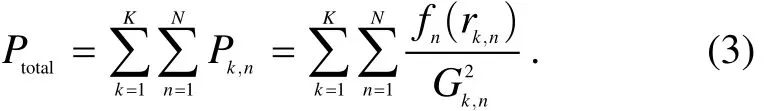
The optimization object is to minimize the total transmitted power subject to the given error rate and transmitted bits, which can be defined as follows

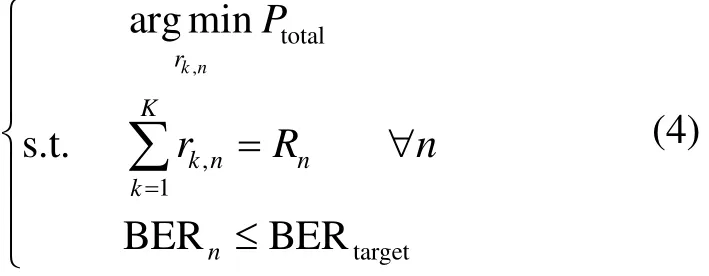
where BERtargetis the upper limit of bit error rate of the system.

3. PSO-GA Algorithm

As we know, GA has the advantages of effective nonlinear programming and scheduling search capacity whereas PSO has good robustness of the initial population and fast convergence. We combine the PSO algorithm with GA algorithm and propose a PSO-GA algorithm. In the improved algorithm, the particle swarm optimizationis used to optimize the system sub-carriers and bits allocation first.When theparticle swarm optimizationis completed, the converged population will be used as the initial population of the genetic algorithm. Then, the genetic algorithm is used to optimize the system sub-carriers and bits allocation.Finally, the optimal solution is obtained.

Let W be the size of particle swarm. Firstly, we generate an array with K elements, which corresponds to the K sub-carriers. The value of array element is set from 1 to N, which corresponds to the N users. That is to say, one sub-carrier is only allocated to one user, and one array is a solution of the optimization problem. We generate randomly W arrays as the initial population. Suppose c1and c2are learning factors, vmaxis the maximum speed of particle, vminis the minimum speed, wstartis the initial inertia weight, and wendis the final inertia weight.

First we use water-filling algorithm to allocate the required transmitted bits to each element (corresponding to each user), and then calculate the total transmitted power of all users for each particle in the population. We define the fitness of particle as follows

The speed and place of particle are renewed as follows

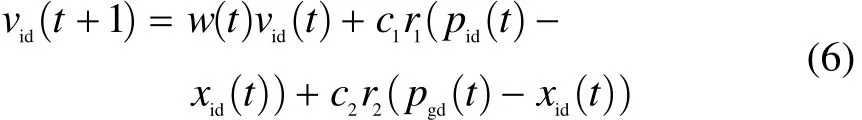
and

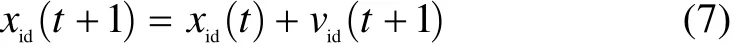
where vid(t+1) is the particle velocity at the iteration of t+1 times, xid(t+1) is the particle position at the iteration of t+1 times, r1and r2are the random values between 0 and 1,pid(t) is the new best fitness value individual (the personal optimal solution place), which is obtained from the comparison of personal fitness value at the iteration of t times with personal best fitness value at the iteration of t-1 times, pgd(t) is the new best individual (the global optimal solution place), which is obtained from the comparison of best fitness value individual in the population at the iteration of t times with the best fitness value individual in the population at the iteration of t-1 times, and w(t) is the inertia weight at the iteration of t times, which is defined as

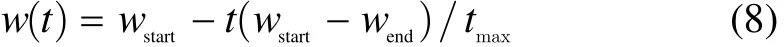
where tmaxis the maximum iteration time, and t is the current number of iterations.

When the updated particle velocity vid(t+1) is higher than the maximum particle velocity vmaxor lower than the minimum particle velocity vmin, a random velocity between vmaxand vminwill be used as the updating particle velocity instead of vmaxor vmin.

Right now, we calculate the total transmitted power of users (renewed particle) according to (3) and the fitness value of the particle according to (5) again. If the best fitness value in the group does not change within the given iteration number or the iteration time is more than the given time, the current population can be taken as the optimal solution. Otherwise, the speed and place of the particle are renewed until the given condition is satisfied.

Now, we take the population got from the termination of iteration of PSO as the initial population of GA.According to the fitness values of all particles in the population, we adopt the optimum maintaining strategy to select the operation, in which the individual with the best fitness will not be involved. There are two operations,crossover operation and mutation operation. In the crossover operation, the PSO-GA algorithm adopts a two-point crossover operation, in which two cross points in two mutual paired individual encoded strings are randomly set and the partial chromosomes between specified two cross points of two individuals are exchanged. In the mutation operation, the PSO-GA algorithm adopts a real value mutation operation, in which each gene locus of individual is specified as the change point according to mutation probability and the genic value is replaced with other allele values.

If the sum of iteration time of the PSO algorithm and GA algorithm is more than the total iteration times of the PSO-GA algorithm Ttotal, the individual with the best fitness in the last time is the optimum allocation plan searched.Otherwise, the selecting operation will be continued until the termination condition is satisfied.

4. Simulation and Analysis

In this section, we present some simulation results of the PSO-GA algorithm proposed in this paper, and compare it with the original PSO algorithm, GA algorithm, and Zhang’s algorithm. The simulating parameters are given in Table 1.

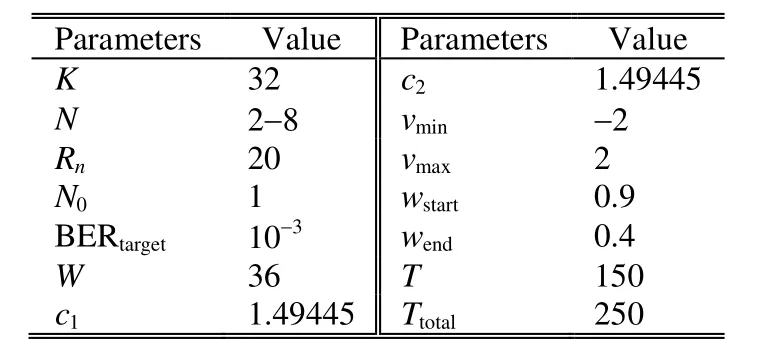
Table 1: Simulation parameters

Fig. 1 describes the total transmitted power of the four algorithms under two users. The total transmitted powers converged by the PSO-GA algorithm, GA algorithm, and Zhang’s algorithm is almost the same, which is better than that of the PSO algorithm. The difference is about 0.5 dB.

Fig. 2 shows the comparison of the transmitted power under four users. The differences between these four algorithms are obvious. The PSO-GA algorithm performs the best, PSO algorithm takes the second place, and Zhang’s algorithm is the worst.

Fig. 3 compares the transmitted power under 6 users. It is observed that the PSO-GA algorithm has 3 dB gain over the PSO algorithm, 4 dB gain over the GA algorithm, and 9 dB gain over the Zhang’s algorithm.

When the user number is 8, the advantage of the PSO-GA algorithm is more visible. It can be observed from Fig. 4 that the PSO-GA algorithm has 3 dB gain over the PSO algorithm, 5 dB gain over the GA algorithm, and 12.5 dB gain over the Zhang’s algorithm, respectively.

From Fig. 1 to Fig. 4, we can conclude that the PSO-GA algorithm requires the least transmitted power among the four algorithms and the performance is the best.As the number of users increases, the gain of PSO-GA algorithm is enhanced.

Fig. 5 shows the advantage of PSO-GA algorithm over the other three algorithms under different number of users.When the user number is larger than 2, the transmitted power of PSO-GA algorithm has 2 dB to 10 dB gain over the other three algorithms.

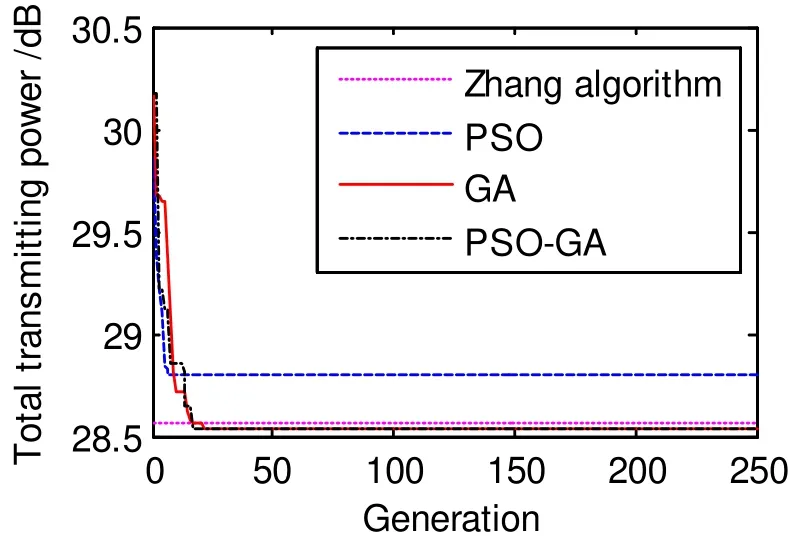
Fig. 1. Comparison of transmitted power under 2 users.

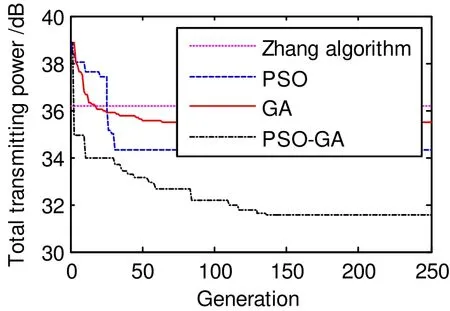
Fig. 2. Comparison of transmitted power under 4 users.

Fig. 3. Comparison of transmitted power under 6 users.

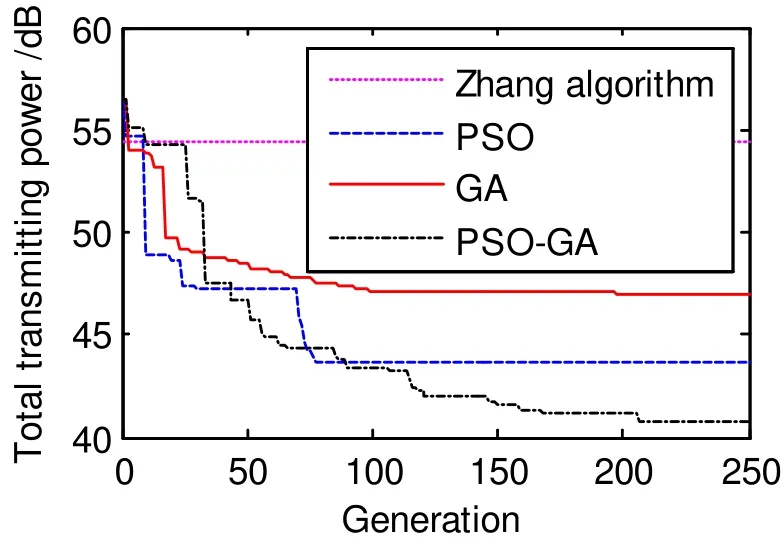
Fig. 4. Comparison of transmitted power under 8 users.

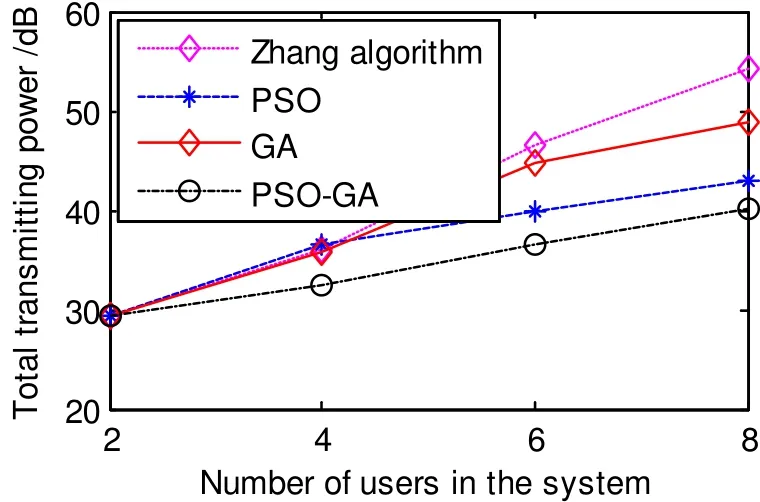
Fig. 5. Comparison of transmitted power under different users.

5. Conclusions

An improved resource allocation algorithm for the multi-user OFDM system is proposed in this paper. We use an improvedPSO algorithm to optimize the system sub-carriers and bits allocation first. When the improved PSO algorithm is converged, the convergence population is used as the initial population of the GA. Then, we use the GA to optimize the system sub-carriers and bits allocation.Simulation results show that the transmitted power of the system by using the proposed algorithm is about 2 dB to 10 dB lower than that of other algorithms.

[1] H. Rohling and R. Gruneid, “Performance comparison of different multiple access schemes for the downlink of an OFDM communication system,” in Proc. of the 47th IEEE Vehicular Technology Conf., Phoenix, 1997, pp.1365–1369.

[2] R. V. Nee and R. Prasad, OFDM for Wireless Multimedia Communications, Boston: Artech House, 1999.

[3] C. Y. Wong, R. S. Cheng, K. B. Letaief, and R. D. Murchet,“Multiuser OFDM with adaptive subcarrier, bit and power allocation,” IEEE Journal on Selected Areas in Communications, vol. 17, no. 10, pp. 1747–1758, 1999.

[4] D. Kivanc and H. Liu, “Subcarrier allocation and power control for OFDMA,” in Proc. of the 11th Asilomar Conf. on Circuits, Systems and Computers, 2000, pp. 147–151.

[5] D. Kivanc, G. Li, and H. Liu, “Computationally efficient bandwidth allocation and power control for OFDMA,”IEEE Trans. on Wireless Communications, vol. 2, no. 6, pp.1150–1158, 2003.

[6] G. Zhang, “Subcarrier and bit allocation for real-time services in multiuser OFDM systems,” in Proc. of 2004 IEEE Int. Conf. on Communications, 2004, pp. 2985–2989.

[7] S. Sadr, A. Anpalagan, and K. Raahemifar, “Radio resource allocation algorithms for the downlink of multiuser OFDM communication systems,” IEEE Commun. Surveys & Tutorials, vol. 11, no. 3, pp. 92–106,2009.

[8] N. Ksairi, P. Bianchi, P. Ciblat, and W. Hachem, “Resource allocation for downlink cellular OFDMA systems—Part I optimal allocation,” IEEE Trans. on Signal Processing, vol.58, no. 2, pp. 720–734, 2010.

[9] N. Ksairi, P. Bianchi, P. Ciblat, and W. Hachem, “Resource allocation for downlink cellular OFDMA systems—Part II:practical algorithms and optimal reuse factor,” IEEE Trans.on Signal Processing, vol. 58, no. 2, pp. 735–749, 2010.

[10] Y. Wang, F. Chen, and G. Wei, “Resource allocation for multi-user OFDM system based on genetic algorithm,”Journal of South China University of Technology, vol. 33,no. 11, pp. 61–65, 2005 (in Chinese).

[11] K. Illanko, K. Raahemifar, and A. Anpalagan, “Sub-channel and power allocation for multiuser OFDM with rate constraints using genetic algorithm,” in Proc. of IEEE Pacific Rim Conf. on Communications, Computers and Signal Processing, 2009, pp. 571–575.

[12] M. Mitchell, An Introduction to Genetic Algorithms.Massachusetts: The MIT Press, 1999, ch. 2.

[13] W. Yang and Q. Li, “A reviews of particle swarm optimization algorithm,” Engineering Sciences, vol. 6, no. 5,pp.7–94, 2004.