有限温度下石墨烯上铁磁超导隧道结中微分电导的研究

潘慧雯,刘 柳,胡亚云,徐金良,李晓薇

(淮阴师范学院 物理与电子电气工程学院,江苏 淮安 223300)

有限温度下石墨烯上铁磁超导隧道结中微分电导的研究

潘慧雯,刘 柳,胡亚云,徐金良,李晓薇

(淮阴师范学院 物理与电子电气工程学院,江苏 淮安 223300)

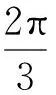
石墨烯; 铁磁体;p-波超导体; 超导隧道结; 微分电导

0 引言

单层石墨片是只有一个原子层厚度的蜂窝状的碳原子晶体,这种理想二维体系显示了不同寻常的奇异特性[1-6],实验上已经发现该体系具有很多新颖的物理性质,例如强磁场下反常的量子霍耳效应[1]、弹道输运[3,4]、Josephson效应[5]、双极性超导特性[6]等.理论上,由于单层石墨片独特的电子结构和无质量费米子的特征,使得人们可以利用低能的凝聚态物理来模拟一些量子场论所预言的相对论量子现象[1,3,4],例如克莱因佯谬[7](Klein paradox).近几年来,有关石墨层上超导隧道结的研究已成为当前凝聚态物理的热点之一.

近来,有很多关于基于石墨层上超导隧道结中准粒子输运性质的研究报道,人们研究了基于石墨层上正常金属/s波和d波超导隧道结、石墨层上铁磁体/s波超导体隧道结中准粒子输运性质[4,9-16],但有限温度下有关基于石墨层上铁磁/p波超导体隧道结中准粒子输运性质的研究还比较少.

本文利用推广的BTK理论讨论有限温度下石墨层上铁磁/p波超导体隧道结中准粒子输运过程,计算结的微分电导.计算结果表明,在有限温度下,微分电导谱的电导峰对应的偏压位置随α的增大从eV=Δ0处向零偏压处移动,磁交换能EhEF时电导随着磁交换能的增强而增大,此时镜面Andreev反射起主导作用.在相同条件下,有限温度下的微分电导随温度T的增大而减少.

1 模型

我们所研究的石墨层上铁磁/p波超导体隧道结的结构如图1所示,x<0处为铁磁态,x>0处为p波超导体.当不考虑准粒子的自旋反转效应时,在石墨层上铁磁/p波超导体隧道结中准粒子的状态可以由DBdG方程描述[8,15]:

(1)

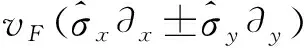
h=EhΘ(-x)

(2)

Δk=Δ±(θ)Θ(x)

(3)

其中Θ(x)是阶跃函数,p波超导体的配对势是各向异性的,电子、空穴的有效配对势是不同的,分别是[19-21]:

Δ±(θ)=±Δ0cos(θ∓α)

(4)

(5)

式中θ为准粒子输运方向相对x轴的夹角,α是p波超导体的a轴与x轴的夹角,由于石墨层上蜂窝状的碳原子晶体结构,α取0和±2π/3[24].式(4)(5)分别是零温和有限温度下的配对势.

考虑电子型准粒子从左边入射的情况,在x<0处的铁磁区域,电子型和空穴型准粒子E>0的本征矢和波矢为:

(6)

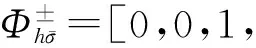
(7)

(8)

EF是铁磁区域的费米能,平行于结方向的粒子的动量是守恒的,满足条件:

(9)

其中θAσ最大值为900,超过900时,Andreev反射是一虚过程虚Andreev反射对电流没有贡献.因此,θσ不能超过:

(10)

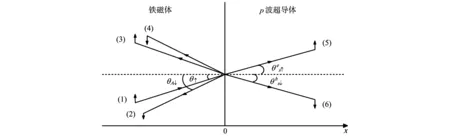
(1) 自旋向上的入射电子空穴 (2) 自旋向下的反向Andreev反射空穴(3) 自旋向上的反射电子 (4) 自旋向下的镜面Andreev反射空穴(5) 自旋向上的透射电子型准粒子 (6) 自旋向下的透射空穴型准粒子

在x>0处的超导体区域,电子型和空穴型准粒子E>0的本征矢和波矢为:

(11)

(13)

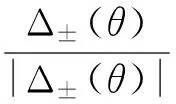
(14)

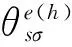
(15)

(16)

(17)

波函数满足的边界条件为[8]:

ψsσ(x=0-)=ψFσ(x=0+)

(18)

(19)

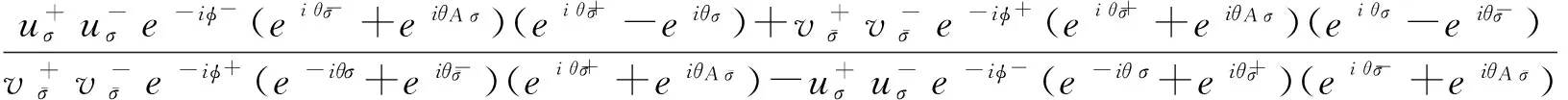
(20)

(21)

(22)

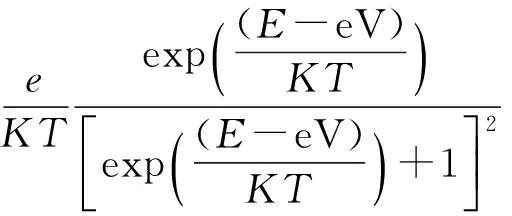
(23)

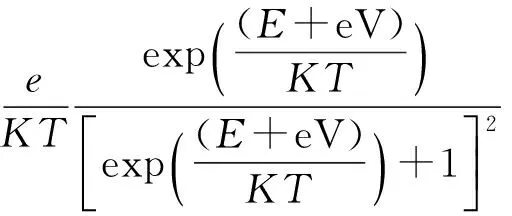
(24)

这里G0是常量,G1G2分别为零温和有限温度下的微分电导.

(25)

Bσ(eV,θ)=|bσ(eV,θ)|2

(26)

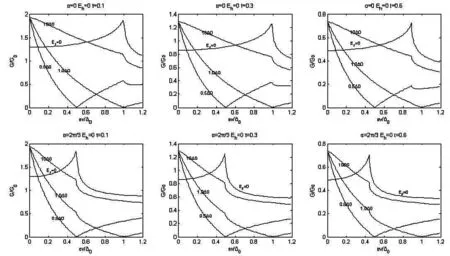
图2 微分电导随偏压V的变化关系曲线

2 计算结果和讨论

3 结论

本文利用推广的BTK理论讨论石墨层上铁磁/p波超导体隧道结中准粒子输运过程,计算了结的微分电导.计算结果表明,在有限温度下,微分电导谱的电导峰对应的偏压位置随α的增大从eV=Δ0处向零偏压处移动,磁交换能EhEF时电导随着磁交换能的增强而增大.微分电导随温度T的增大而减少;EF≠0的零偏压电导值比零温度下的对应值小.

图3 微分电导随偏压V的变化关系曲线

[1]Novoselov K S,Geim A K,Mozorov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306:666-669.

[2]Morozov S V,Novoselov K S,Katsnelson M I,et al.Strong Suppression of Weak Localization in Graphene[J].Phys Rev Lett,2006,97:016801.

[3]Novoselov K S,Geim A K,Mozorov S V.et al Two-dimensional gas of massless Dirac fermions in grapheme[J].Nature,2005,438:197-200.

[4]Zhang Y B,Tan Y W,Stormer Horst L,et al.Experimental Observation of Quantum Hall Effect and Berry’s Phase in Graphene[J].Nature,2005,483:201-204.

[5]Titov M,Beenakker C W J.Josephson effect in ballistic grapheme[J].Phys Rev B,2006,74:041401.

[6]Heersche Hubert B,Jarillo-Herrero Pablo,Ostinga Jeroen B,et al.Bipolar supercurrent in grapheme[J].Nature,2007,446:56-59.

[7]Katsenlson M I,Novoselov K S,Geim A K.Chiral tunnelling and the Klein paradox in graphene[J].Nature Phys,2006,2:620-625.

[8]Beenakker C W J,Specular Andreev Reflection in Graphene[J].Phys Rev Lett,2006,97:067007.

[9]Bhattacharjee S,Sengupta K.Tunneling Conductance of Graphene NIS Junctions[J].Phys Rev Lett,2006,97:217001.

[10]Linder J,Sudbo A.Dirac Fermions and Conductance Oscillations ins-andd-Wave Superconductor-Graphene Juncti-ons[J].Phys Rev Lett,2007,99:147001.

[11]Linder J,Sudbo A.Tunneling conductance in s-and d-wave superconductor-graphene junctions:Extended Blonder-Tinkham-Klapwijk formalism[J].Phys Rev B,2008,77:064507.

[12]Zareyan M,Mohammadpour H,Moghaddam A G.Andreev-Klein reflection in graphene ferromagnet-superconductor junctions[J].Phys Rev B,2008,78:193406.

[13]Asano Y,Yoshida T,Tanaka Y,et al.Electron transport in a ferromagnet-superconductor junction on grapheme[J].Phys Rev B,2008,78:014514.

[14]Zhang Q Y,Fu D Y,Wang B G,et al.Signals for Specular Andreev Reflection[J].Phys Rev Lett,2008,101:047005.

[15]Hsu Y F,Guo G Y.Tunneling conductance of graphene ferromagnet-insulator-superconductor junctions[J].phys Rev B,2010,81:045412.

[16]Bai C X,Yang Y L.Tunneling conductance in graphene-based normal metal-insulator-superconductor junctions[J].Physics Letters A,2010,374:882-885.

[17]Andreev A F.The thermal conductivity of the intermediate state in superconductors[J].Sov Phys JETP,1964,19(5):1228-1231.

[18]Blonder G E,Tinkham M,Klapwijk T M.Transition from metallic to tunneling regimes in superconducting microconstrictions:Excess current charge imbalance and supercurrent conversion[J].Phys Rev B,1982,25:4515.

[19]Hirai T,Tanaka Y,Yoshida N,et al.Temperature dependence of spin-polarized transport in ferromagnet/unconventional superconductor junctions[J].phys Rev B,2003,67:174501.

[20]Tanaka Y,Kashiwaya S.Anomalous charge transport in triplet superconductor junctions[J].phys Rev B,2004,70:12507.

[21]Roy Bitan,Herbut Igor F.Unconventional superconductivity on honeycomb lattice:Theory of Kekule order parame-ter[J].phys Rev B,2010,82:035429.

[责任编辑：蒋海龙]

Tunneling Conductance in Graphene Ferromagnet/pWave Superconductor Junctions at Finite Temperature

PAN Hui-wen,LIU Liu,HU Ya-yun,XU Jin-liang,LI Xiao-wei

(School of physics and electronic electrical engineering,Huaiyin Normal University,Huaian Jiangsu 223300,China)

Using the extended Blonder-Tinkham-Klapwijk formalism,we investigate the conductance spectra of graphene ferromagnet/pwave superconductor junctions at finite temperature.It is found that the conductance spectra at finite temperature are affected by the p wave pairing symmetry.The ferromagnetic exchange energy in the ferromagnet can suppress Andreev retroreflection but enhance the specular Andreev reflection in graphene ferromagnet/pwave superconductor junctions.The conductance decreases at finite temperature with increasing exchange energyEhforEhEF.

graphene; ferromagnet;p-wave superconductor; superconductor junctions; differential conductance

O511

:A

:1671-6876(2015)01-0024-06