蒙古栎天然林单木生长模型研究——Ⅲ.单木枯死模型

马 武,雷相东,徐 光,杨英军,王全军

(1 中国林业科学研究院 资源信息研究所，北京 100091；2 西弗吉尼亚大学，美国Morgantown WV 26505；3 吉林省汪清林业局，吉林 汪清 133200)

蒙古栎天然林单木生长模型研究
——Ⅲ.单木枯死模型

马 武1,2,雷相东1,徐 光3,杨英军3,王全军3

(1 中国林业科学研究院 资源信息研究所，北京 100091；2 西弗吉尼亚大学，美国Morgantown WV 26505；3 吉林省汪清林业局，吉林 汪清 133200)

【目的】 研究蒙古栎天然林的单木枯死模型，为蒙古栎天然林的合理经营提供依据。【方法】 以蒙古栎天然林为研究对象，基于吉林省汪清林业局195块固定样地的2期复测数据，采用二分类的Logistic回归方法建立蒙古栎天然林的单木枯死模型。【结果】 期初胸径、竞争指数、林分密度都是显著影响树木枯死的因子，林木直径是影响林木枯死的重要因子，直径越小，枯死概率越大。χ2检验结果以及ROC(Receiver operating characteristic)曲线显示，使用Logistic回归可以有效预测树木的枯死情况，所建模型较合理。【结论】 建立的单木枯死模型统计可靠，可为吉林省汪清地区蒙古栎天然林的生长预测提供依据。

蒙古栎天然林；Logistic回归方法；单木枯死模型

林木枯死在维持种群动态变化、物种多样性和结构多样性等方面有重要的作用，枯死模型是了解森林演变的重要模型，也是林分生长与收获模型体系中重要的一个组成部分[1]，但至今研究仍较少，其原因主要是由于树木死亡是小概率事件，难以收集到足够的数据进行分析。林木的枯死概率通常因树木大小、活力状况、树种、林分密度、树种组成、立地质量和生长空间等的不同而异。随着计算机技术的飞速发展，径阶或单木枯死概率模型已经是枯死模型研究的重点。根据枯死原因，可将径阶或单木枯死概率模型分为由竞争引起的枯死概率模型和非竞争引起的枯死概率模型。由竞争引起的枯死概率模型主要用于预测由于林分对空间、养分和水分等的竞争产生生长胁迫而导致林木的枯死。非竞争引起的枯死概率模型主要用于预测由各种干扰，如火灾、病虫害、暴风雨等引起的林木死亡[2]。

单木枯死概率模型根据所选自变量的不同，又可分为包含密度指标的枯死概率模型和不包含密度指标的枯死概率模型2类，不包含密度指标的枯死概率模型主要是根据树木的胸径和直径生长量来预测树木的死亡率大小[3]。目前，包含密度指标的枯死概率模型已经是模拟林木枯死概率模型研究的重点。有研究者认为，树冠竞争因子与模拟林木枯死概率之间有密切的关系[4]；也有研究者认为，胸高断面积与林木枯死概率之间关系密切，还有人认为树冠率(冠长与树高的比值)也对枯死概率模拟起到一定的作用[5]。国内外估测林木死亡率的主要技术方法包括利用回归模型和分布函数构成叠加模型估计枯死量[6]、概率密度函数估计枯死量[7]、线性回归或非线性回归分析[8]以及Logistic模型[2,9-13]。其中大多数研究者都使用Logistic模型来拟合林木的枯死概率模型，并取得了很好的模拟精度和适应性。本研究以东北过伐林区的蒙古栎天然林为对象，建立其单木枯死模型，预测其定期枯死情况，以期为蒙古栎合理经营决策的制定和发掘其经营潜力提供依据。

1 研究地区概况

见文献[14]。

2 数据来源与研究方法

2.1 数据来源

建模数据来源见文献[14]。将1997年和2007年的2次测定值作为一个独立的单元看待，共有13 360个单元。随机选取80%的数据用于建模，20%的数据用于模型检验。数据使用SPSS 16.0统计软件进行处理。本研究建模数据的主要统计量见表1。由表1可以看出，林木的平均期初胸径为 12.35 cm，介于5.00～72.00 cm；林分密度介于 533～3 067 株/hm2。用于建模的160个样地的两期数据中共有152个样地发生枯死，这些样地有较好的代表性。由各径阶林木株数和枯死株数分布(图1)可以看出，枯死主要发生于较小径阶的林木。

表1 吉林省汪清林业局蒙古栎林单木枯死模型建模数据自变量的统计量(n=10 698)Table 1 Statistics of independent variables for individual-tree mortality model of Mongolian oak forests in Wangqing Forest Bureau,Jilin province (n=10 698)

注：D.单木期初胸径(cm)；G.林分断面积(m2/hm2)；V.林分蓄积量(m3/hm2)；N.林分密度(株/hm2)；ΔDg.林分断面积平均胸径10年间的生长量(cm)；E.样地海拔(m)。

Note:D.Initial diameter of invidual tree (cm)；G.Basal area per hectare (m2/hm2)；V.Volume per hectare (m3/hm2)；N.Stand density (Trees/hm2)；ΔDg.Increment of average diameter at breast height (DBH) from stand basal area in 10 years (cm)；E.Elevation (m).

2.2 研究方法

本研究采用Logistic回归方法建立蒙古栎天然林的单木枯死模型。Logistic回归模型形式的优点在于：函数值在0～1，可以限制枯死概率预估值的范围；选择适当的变量就可以描述大多数自然发生的枯死类型；非线性估计技术可有效地估计该函数的参数。Logistic模型形式如下：

(1)

式中：Pi为第i株树10年后的枯死概率；x1，x2，…，xn为选择的自变量；a0，a1，…，an为待定参数。

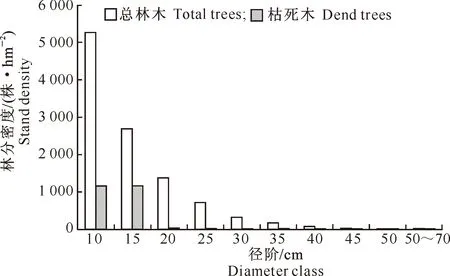
图1 吉林省汪清林业局蒙古栎林各径阶总林木和枯死木的林分密度Fig.1 Distribution of total trees and dead trees by diameter for Mongolian oak forests in Wangqing Forest Bureau,Jilin province

因变量为包含0-枯死和1-存活的二分类变量。从模型来看，函数Pi对x在Pi=0或Pi=1附近的变化反应不敏感，并且具有高度的非线性特性，因此在上述方程的基础上，求出林木枯死不发生的概率，然后得到林木枯死发生概率与不发生概率之比，并取自然对数，使得函数在0或1附近时的变化幅度较大：

(2)

这种转换后的形式使模型成为不受约束的一个线性函数，这种形式称为Logit形式，或对数发生比[2]。

2.3 单木枯死模型自变量的选择及参数估计

树木大小、生命力、林分密度、树种组成、立地质量等因子均能对枯死产生重要影响。Hamilton[15]曾将变量分为4组：单木大小、单木竞争、单木活力和林分密度。由于单木活力不能直接测量，一些文献中使用树木生长或树冠透光度来替代[16-17]。为了考虑环境对树木的长期影响，在模型中一般加入立地因子来体现，因为海拔、坡向、坡度等立地因子的交互作用对林分生产力、树种组成能产生重要影响，基于前人的研究结果[2,10,13]，本研究将自变量分为4部分：单木大小、单木竞争、林分因子和立地条件，可表示为：

b′x′=b0+b1V1+b2V2+b3V3+b4V4。

(3)

式中：b0是常数项，b1、b2、b3、b4是参数，V1为单木大小，V2为单木竞争，V3为林分因子，V4为立地条件。各变量见表2。

表2 单木枯死模型的自变量及说明Table 2 Indenpendent variables and their description in the individual-tree motality model

注：A.坡向值，正北方为0°，正西方为90°，正南方为180°，正东方为27°；S.坡度值。

Note:A.Slope aspect,due north is 0°,due west is 90°,due south is 180°,due east is 270°；S.Slope.

考虑到模型的应用，与大多数文献相同，本研究竞争指数采用与距离无关的指数，并使用多元线性回归对入选自变量进行筛选，用方差膨胀因子(VIF)来判断自变量间的多重共线性。因为一些自变量间存在共线性，会产生较大的参数标准误，使方程的预测变得不可靠，因此只有VIF<5的因子才可进入模型。参数的计算采用基于最大似然估计的向前逐步回归法，所有计算通过SPSS 16.0完成。

2.4 单木枯死选定模型的检验

树木枯死的概率值是通过Logistic 回归模型得到的，因此需要通过一个临界概率值将其转化为二分类变量才能用于预测。临界概率值的确定主要包括以下方法：(1) 0.5法则。一般而言，若无任何先验知识的支撑，对于任意单木，其枯死的概率是0.5，即枯死与存活的概率相等。(2) Kappa极大值法。(3) 最大总结阈值原则(Maximum summary threshold，MST)。(4) Bayes公式。其目的是通过阈值来提高模型预测的精度。单木枯死模型观测值和预测值的列联表见表3。

表3 单木枯死模型观测值和预测值的列联表Table 3 Contingency table of the observed and predicted values by individual-tree mortality model

注：a11.正确预测树木枯死的株数，a12.错误预测树木枯死的株数，a21.错误预测树木存活的株数，a22.正确预测树木存活的株数，A1m.枯死观测株数，A2m.存活观测株数，An1.枯死预测株数，An2.存活预测株数，An m.总株数。

Note:a11.Correctly predicted number of dead trees，a12.Uncorrectly predicted number of dead trees，a21.Uncorrectly predicted number of survived trees，a22.Correctly predicted number of survived trees，A1m.Observed dead trees，A2m.Observed survived trees，An1.Predicted dead trees，An2.Predicted survived trees，An m.Total trees.

使用穷举法计算100个临界概率(0～1，以0.01为间隔)的敏感度、特异度(敏感度=a11/A1m，特异度=a22/A2m)。特异度为正确预测树木存活数与观测存活数的比值，敏感度为正确预测树木枯死数与观测枯死数的比值。由于Kappa极大值法难以预测样本数量较少的情况，而Bayes公式受主观影响较大，在此采用MST原则，即选取敏感度、特异度之和最大时的概率阈值[2]。

模型精度检验分模型拟合效果和拟合优度检验2个方面。模型拟合优度用来检验当前模型是否有统计学意义。对于二分类变量而言，拟合优度的检验通常有Pearson-χ2检验、Deviance检验、似然比检验及拟合优度检验(Hosmer-Lemeshow)等多种方法。在将重要的预测指标分级计算的情况下，最为灵活合适的是Pearson-χ2检验。通过Pearson拟合优度检验计算不同分类的χ2值：

(4)

式中：χ2是自由度为n的统计值，NDobs和NDpred分别为不同分组(树种、期初胸径等)死亡树木数量的观测值和预测值。

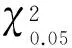
3 结果与分析

3.1 蒙古栎林单木枯死模型的确定

由表4可知，蒙古栎单木枯死模型的所有参数均极显著，方差膨胀因子均小于5。发生比率表示自变量每增加1个单位，枯死发生概率与存活概率的比值是自变量变化前相应比值的倍数，根据其值是否大于1，可以判断发生枯死的可能性，大于1表示枯死发生的可能性会提高，小于1则降低。另外本研究临界概率值的确定采用MST原则，敏感度、特异度之和最大时的概率阈值为0.30。从表4可以看出，单木期初胸径(D)、竞争指数、林分密度(N)都显著进入模型变量，枯死概率与单木期初胸径成反比，即直径越大，枯死概率越小；林分断面积平均胸径10 年间生长量(ΔDg)显示生长快的树木活力强，从而枯死概率小；竞争指数(BAL)与林分因子(BAP)也是影响枯死概率的重要变量，即竞争力强的树木枯死概率小；林分密度(N)与林分断面积(G)是对单木枯死有极显著影响的变量，且其发生比率大于或接近于1，与自然稀疏规律一致。

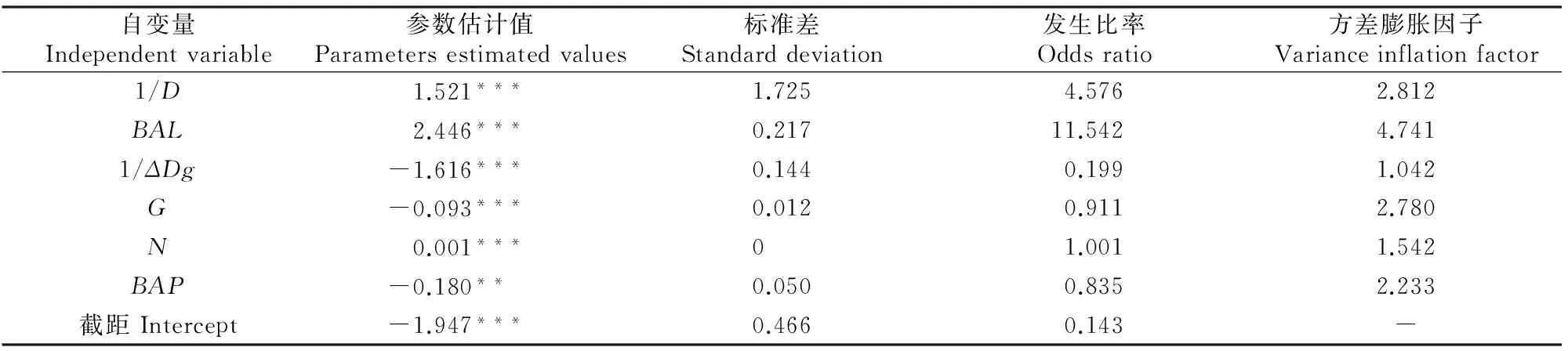
表4 蒙古栎林单木枯死模型的参数估计值Table 4 Estimated parameters of individual-tree mortality model for Mongolian oak forests

注：各自变量含意同表2。*表示P<0.05，**表示P<0.01，***表示P<0.001。

Note:The meanings of variables are the same as in table 2.*meansP<0.05，**meansP<0.01，***meansP<0.001.

3.2 蒙古栎林单木枯死模型的检验

从选定的蒙古栎单木枯死模型的χ2检验结果(表5)来看，实际枯死株数与预测枯死株数间无显著差异，说明建立的蒙古栎单木枯死模型有良好的解释性和预测性。由图2可知，该模型ROC曲线下面积(AUC)为0.753，说明选定的单木枯死模型诊断价值良好。

由图3可以看出，在胸径较小时，蒙古栎枯死模型的预测值与实测值较为接近；但在胸径较大，尤其是大于35 cm时，预测的效果不是很好，其原因是大径阶样本量较少所致。总体而言，本研究所建立的枯死概率模型统计上较合理。

表5 蒙古栎林单木枯死模型建模数据和检验数据预测与观测枯死株数的χ2检验Table 5 χ2 test in predicted and observed dead trees for calibration and validation data of individual-tree mortality model for Mongolian oak forests

注：ns表示不显著。

Note: ns means insignificant.

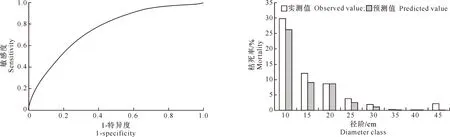
图2 选定的蒙古栎林单木枯死模型的ROC曲线Fig.2 ROC curve of selected individual-tree mortality model for Mongolian oak forests

4 讨论与结论

本研究以蒙古栎天然林为对象，基于吉林省汪清林业局195块固定样地的2期复测数据，采用二分类的Logistic回归方法，考虑自变量间的共线性，从单木大小、单木竞争、林分因子和立地条件4个方面构建了蒙古栎林10年间单木枯死模型。结果表明，枯死概率与单木期初胸径(D)、林分断面积平均胸径10 年间生长量(ΔDg)成反比，即直径大、生长快的树木枯死概率小；竞争指数(BAL)与林分因子(BAP)也是影响枯死的重要变量，竞争力强的树木枯死概率小；林分密度(N)与林分断面积(G)是对单木枯死有显著影响的变量，且其发生比大于或接近于1，与自然稀疏规律一致。说明期初胸径、竞争指数、林分密度都是显著影响树木枯死的因子，其中林木胸径是影响林木枯死最重要的因子，胸径越小，枯死概率越大。上述结果与有关学者的研究结论[2,9,12-13,18]一致。对选定的蒙古栎单木枯死模型进行χ2检验，结果表明实测枯死株数与预测枯死株数无显著差异，说明建立的单木枯死模型有良好的解释性和预测性；模型的ROC曲线显示，使用Logistic回归可以有效地反映树木的枯死情况，所建单木枯死模型合理，可以很好地描述和预测蒙古栎林木的生长，为蒙古栎林的经营决策提供强有力的依据。

相对于人工林，天然林一般由多个树种组成，树种间的相互作用和关系非常复杂，复层现象明显，树木间竞争和生长及周围环境关系随时间变化[19]。这些问题制约着天然林生长模型的建立和使用,尤其是对单木枯死模型的研究。对于树种组成和树冠的问题，由于本研究蒙古栎天然林的树种组成中，蒙古栎占70%以上，部分样地甚至达100%，其他树种的组成均在30%以下，部分样地更低，因此本研究只将蒙古栎归为一类，并没有考虑不同树种之间的竞争对单木枯死的影响。另外，由于大部分蒙古栎天然林处于幼、中龄林阶段，平均期初胸径仅为 12.35 cm，这一时期树冠对枯死的影响并不明显，所以本研究没有考虑树冠对枯死的影响。然而对于与距离无关的林木竞争因子和立地因子，本研究综合考虑各竞争因子的特点和数据情况，对模型的实用性已进行了详细讨论。

此外，像其他森林生长数据一样，本研究采用的蒙古栎林样地生长观测数据具有重复性和相关性等特点，下一步可考虑采用混合效应模型方法对该模型进行更新，以进一步提高模型的估计效果。

[1] 刘 平，马履一，贾黎明，等．油松林木枯损率模型研究 [J].林业资源管理，2008(2)：51-56．

Liu P，Ma L Y，Jia L M，et al．Study on tree mortality model forPinustabulaeformisplantation [J].Forest Resources Management，2008(2)：51-56．(in Chinese)

[2] 向 玮，雷相东，刘 刚，等．近天然落叶松云冷杉林单木枯死模型研究 [J].北京林业大学学报，2008，30(6)：90-98．

Xiang W，Lei X D，Liu G，et al．Individual tree mortality models for semi-natural larch-spruce-fir forests in Jilin Province,Northeastern China [J].Journal of Beijing Forestry University，2008，30(6)：90-98．(in Chinese)

[3] 李凤日．落叶松人工林林分动态模拟系统的研究 [D].北京：北京林业大学，1994．

Li F R．Simulation system research of stand dynamic forLarixgmeliniiplantation [D].Beijing：Beijing Forestry University，1994．(in Chinese)

[4] Thomas N L．Modeling individual tree growth from data with highly irregular measurement intervals [J].Forest Science，2006， 52(2)：198-208．

[5] Quang V C．Prediction of annual diameter growth and survival for individual trees from periodic measurements [J].Forest Science，2000，46(1)：127-134．

[6] 胡晓龙．林分枯死模型的研究 [J].林业科学研究，1996，9(5)：525-529．

Hu X L．Research of stand motality model [J].Forest Research，1996，9(5)：525-529．(in Chinese)

[7] 龚直文．长白山退化云冷杉林演替动态及恢复研究 [D].北京：北京林业大学，2009．

Gong Z W．Dynamics of fprest succession and restoration strategies for degraded spruce-fir forest in Changbai Mountain [D].Beijing：Beijing Forestry University，2009．(in Chinese)

[8] 李生英，喻利华，王秀芬．林分直径枯损模型分析与研究 [J].辽宁林业科技，1999(3)：11-13．

Li S Y，Yu L H，Wang X F．Analysis and research of stand diameter motality model [J].Journal of Liaoning Forestry Science and Technology，1999(3)：11-13．(in Chinese)

[9] Trasobares A，Tome M，Miinac J．Growth and yield model forPinushalepensisMill.in Catalonia,north-east Spain [J].Forest Ecology and Management，2004，203：49-62．

[10] Lexer∅d N L．Growth and yield models for uneven-sized forest stands in Finland [J].Forest Ecology and Management，2005，206：91-108．

[11] Namaalwa J，Eid T，Sankhayan P．A multi-species density-dependent matrix growth model for the dry woodlands of Uganda [J].Forest Ecology and Management，2005，213：312-327．

[12] Bravo-Oviedo A，Sterba H，Bravo F．Competition-induced mo-rtality for Mediterranean Pinus pinaster Ait. andP.sylvestrisL. [J].Forest Ecology and Management，2006，222：88-98．

[13] Pukkala T，Lahde E，Laiho O．Growth and yield models for uneven-sized forest stands in Finland [J].Forest Ecology and Management，2009，258：207-216．[14] 马 武，雷相东，徐 光，等．蒙古栎天然林单木生长模型的研究：Ⅰ．直径生长量模型 [J].西北农林科技大学学报：自然科学版，2015，43(2)：99-105.

Ma W，Lei X D，Xu G，et al．Growth models for naturalQuercusmongolicaforests:Ⅰ.Diameter growth model [J].Journal of Northwest A&F University：Natural Science Edition，2015，43(2)：99-105.(in Chinese)

[15] Hamilton D A．Extending the range of applicability of an individual tree mortality model [J].Canadian Journal of Forest Research，1994，20：1212-1218．

[16] Biging G S，Dobbertin M．A comparison of distance dependent competition measures for height and basal area growth of individual conifer trees [J].Forest Science，1992，38(3)：695-720．

[17] Kramer H．Crown development in conifer stands in Scotland as influenced by initial spacing and subsequent thinning treatment [J].Forestry，1966，39：40-58．

[18] Mehmet M，Nuray M，Hakki Y．Modeling individual tree mortality for crimean pine plantations [J].Journal of Environmental Biology，2007，28(2)：167-172．

[19] 包昱君．汪清林业局云冷杉林单木生长模型的研究 [D].北京：北京林业大学，2013．

Bao Y J．Individual tree modeling for spruce-fir forest in Wangqing [D].Beijing：Beijing Forestry University，2013．(in Chinese)

Growth models for natural Mongolian oak forests ——Ⅲ.Individual-tree mortality model

MA Wu1,2,LEI Xiang-dong1,XU Guang3,YANG Ying-jun3,WANG Quan-jun3

(1InstituteofForestResourceInformationTechniques,ChineseAcademyofForestry,Beijing100091,China; 2WestVirginiaUniversity,Morgantown26505,America;3WangqingForestryBureauinJilinProvince,Wangqing,Jilin133200,China)

【Objective】 Aiming to provide foundation for reasonable management of Mongolian oak natural forests,individual-tree mortality model was researched.【Method】 The data used to develop individual-tree mortality model for predicting Mongolian oak natural forests were collected from 195 re-measured permanent sample plots in Wangqing Forest Bureau,Jilin province.Then,the individual-tree mortality model for Mongolian oak natural forests was developed using binary logistic regression method. 【Result】 The initial diameter at breast height,competition index,and stand density (number of trees per hectare) had significant effects on tree mortality.The mortality probability increased as the decrease of diameter.Chisquare-Test (χ2) and receiver operating characteristic (ROC) curve showed that the binary logistic could effectively predict death of trees.【Conclusion】 The established individual-tree mortality model was reliable to predict the growth of Mongolian oak natural forests in Wangqing region,Jilin province.

natural Mongolian oak forest;logistic regression method;mortality model

2014-06-10

国家“十二五”科技支撑计划项目“长白山过伐林可持续经营技术研究与示范”(2012BAD22B02)

马 武(1986-)，男，湖南湘潭人，在读博士，主要从事森林资源经营与管理研究。E-mail：wuma@mix.wvu.edu

雷相东(1972-)，男，河南洛阳人，研究员，博士生导师，主要从事森林生长模型与模拟研究。E-mail:xdlei@caf.ac.cn

时间:2015-03-12 14:17

10.13207/j.cnki.jnwafu.2015.04.035

S792.186

A

1671-9387(2015)04-0059-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20150312.1417.035.html