直驱式小型风力发电机MPPT控制
2015-07-11巩建英谢蓉
巩建英,谢蓉
(1.长安大学电子与控制学院,陕西西安710064;2.西北工业大学自动化学院,陕西西安710072)
近年来,随着新能源技术的发展,风力发电的成本不断降低,从而使得全球范围内风力发电机(wind turbine,WT)的安装容量剧增[1-2]。其中,新安装的很大一部分为小型风力发电机(small wind turbine,SWT)[3-4]。在我国偏远的哨所、农牧区、气象站和微波站安装SWT,具有很好的经济性和实用性[5]。
目前,机械结构配置较为简单的SWT是由风力涡轮机和永磁同步发电机(PMSG)构成的变转速型风力发电机[6-7]。其中发电机由风力涡轮机直接驱动,由于没有变速箱,其具有机组寿命长、维护方便、效率高和成本低等优点,但缺点是发电机的转速将随着风场风速的变化而变化,实现最大功率点跟踪(MPPT)控制比较困难[6-7]。具体体现为,若使用风速和转速等机械传感器来回馈控制器设计所需的状态参数,将增加SWT的配置和控制成本并降低其可靠性,若不使用机械传感器获得控制器设计所需的转速等状态参数,将会增加控制器设计的难度,甚至会产生较大的MPPT跟踪误差。
为了实现对直驱式SWT的MPPT控制目标,已有的研究成果主要包括以下几类。
1)不使用风速传感器且不知道SWT 的模型参数,采用干扰和观测(P&O)方法实现MPPT 控制[8-9]。这种方法的主要不足是风速变化容易引起发电机输出电压较大的波动,且存在较大的跟踪误差。
2)使用位置传感器而不使用风速传感器,采用基于ω—P曲线的方法实现MPPT控制[10-13]。这种方法具有很好的控制效果,其主要不足是使用了机械传感器,降低了风力发电机组的可靠性,增加了控制成本。
3)不使用任何机械传感器,采用不可控三相整流桥将PMSG 的输出电压整流为直流电压Vdc,然后使用了基于Vdc—P 或Vdc—Idc曲线的方法实现MPPT 控制[7,14-16]。这种方法的不足之处是整流器输出端电压Vdc与风力涡轮机的机械角速度ω之间的对应关系较为复杂,需要分别考虑整流器工作在CCM,DCM 和NCM 等3 种模式下Vdc与ω之间的对应关系,增加了系统建模和控制过程中理论分析和计算的难度。
为了不增加风力发电系统建模和控制过程中理论分析和计算的难度,本文在建立由风力涡轮机和PMSG 组成的风力发电机组的数学模型的基础上,通过理论分析得知PMSG输出端电压的有效值U与其角速度ω之间存在近似的线性关系,提出了利用U—P 曲线代替ω—P曲线进行MPPT控制的方法。
该方法通过对PMSG 输出端电压和电流进行采样,并计算出输出功率Pout=3UI,以获得U 与P 的实时对应关系,然后通过与预定的U—P 曲线进行比较来对SWT 的角速度进行调整,以实现对该风力发电机组的MPPT 控制。最后,用Matlab 仿真验证该模型和控制方法的有效性。
1 问题描述
SWT 的结构原理如图1 所示。其中包括风力发电机组、整流器、卸载箱、蓄电池、逆变器和负载等。
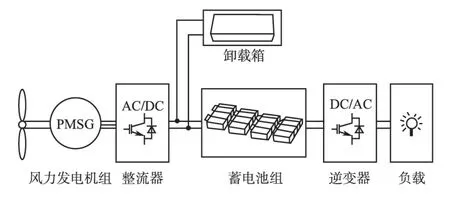
图1 小型风力发电系统结构图Fig.1 The structure of SWT
下面建立SWT中主要模块的数学模型。
1.1 风力涡轮机的模型
一般而言,采用WT捕获风能时,由风能转换成的机械功率为[2]
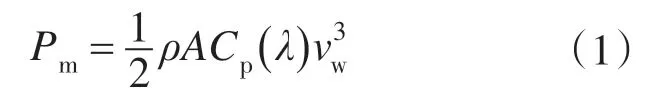
式中:ρ为空气密度;A为桨叶扫过的面积;vw为风速;Cp(λ) 为性能系数;λ为叶尖速比,λ=ωtR/vw,ωt为风力涡轮机的角速度;R为桨叶半径。
SWT的桨距角(β)通常是固定的。当桨距角为常数β0时,Cp(λ) 描述为[2]

1.2 PMSG模型
PMSG在dq坐标系下的数学模型为[17]
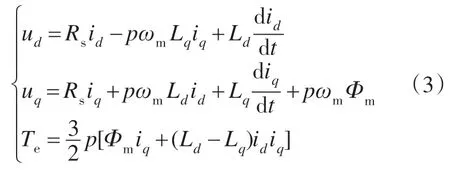
式中:ud,uq分别为d轴和q轴端电压;id,iq分别为d 轴和q 轴电流;Ld,Lq分别为d 轴和q 轴电感;Rs为电枢电阻;ωm为转子角速度;p为极对数;Φm为永磁感应磁通;Te为电磁转矩。
SWT 中的PMSG 通常设计为隐极永磁转子同步发电机,故Ld=Lq。由于PMSG 与风力涡轮机直接轴联,可以认为PMSG的转子角速度ωm与风力涡轮机的角速度ωt相等,即ωm=ωt。下文中将表示风力涡轮机和PMSG 的机械角速度均写为ωm。
SWT的机械运动方程可写为

式中:Tm为SWT 的机械转矩;J为SWT 的惯性转矩;B为负荷黏滞性摩擦因数。
2 控制器设计
对SWT进行MPPT控制的目的是,当实际风速vw低于额定风速vwN时,使得SWT 运行在最大风功率电追踪状态下;当vw大于vwN时,必须减少风力涡轮机风轮捕获的能量,使功率保持在额定值附近,以保护SWT的安全。
2.1 利用ω—P曲线实现MPPT控制
根据式(1),给定风速vw,风力涡轮机的最大输出功率Pm,opt取决于其性能系数Cp(λ)。当Cp(λ)为最大值Cpopt时,风力涡轮机的输出功率为最大值Pm,opt,即
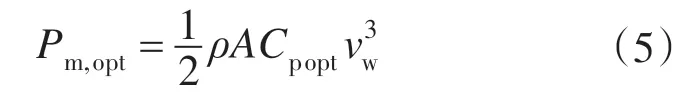
其中,Cpopt对应于最优叶尖速比λopt。
根据λ=ωmR/vw可知,通过调整角速度ωm来适应风速vw的变化,能够使得叶尖速比λ保持在最优值λopt。因此,在风速vw下,存在一个最优的角速度ωm,opt能够使得风力涡轮机的输出功率达到最大值Pm,opt。
根据ωm与Pm,opt之间的对应关系可以获得ω—P曲线,如图2所示。
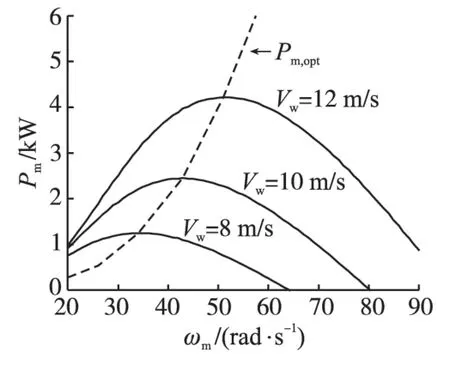
图2 ω—P曲线Fig.2 The curves of ω—P
图2中,实线表示风力涡轮机的输出功率Pm与角速度ωm的关系曲线;虚线表示风力涡轮机的最优输出功率Pm,opt与ωm的关系曲线。
小型风力涡轮机的参数为:额定功率4.2 kW,启动风速3.5 m/s,额定风速12 m/s,最优性能系数0.316,最优叶尖速比8.63,转动惯量5 kg·m2,风轮直径4 m,额定转速600 r·min-1,电枢电阻0.6 Ω,电枢电感4.9 mH,极对数15,永磁感应磁通0.475 Wb。
使用传感器获得ωm的取值,利用ω—P曲线完全可以实现MPPT 控制[4,12]。若不使用传感器获得ωm的取值,利用U—P曲线也能够进行MPPT控制。下面给出其相应的控制原理。
2.2 利用U—P 曲线实现MPPT控制
采用直驱式永磁同步发电机组进行风力发电,由于发电机采用永磁体励磁时,发电机与连接在其输出端的永磁体之间没有无功功率交换,因此发电机在d轴和q轴的反电势分别为
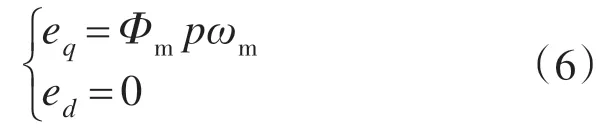
式中:ed,eq分别为PMSG在d轴和q轴的反电势。
由于d 轴电流分量与无功功率相关,因此设d轴电流在稳态时为0,即id=0。通过Park变换,可求得
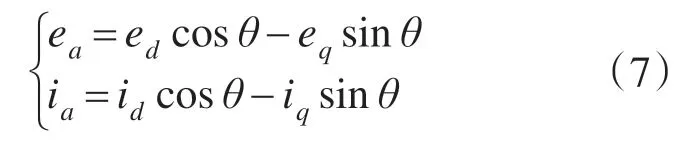
式中:θ=pωmt;ea,ia分别为PMSG 在abc 坐标下a相的反电势和电枢电流。
根据式(7),ea和ia的有效值分别为
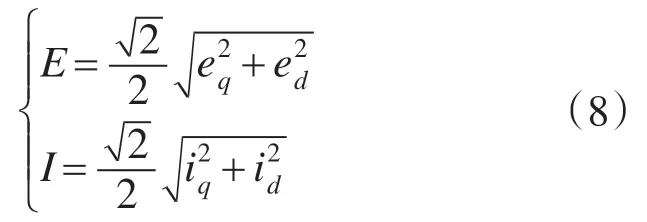
式中:E,I分别为ea和ia的有效值。
PMSG的电磁功率可通过下式求得

PMSG的输出功率为

式中:U为PMSG在abc坐标系下的输出端电压ua的有效值。
将式(6)和id=0代入式(8),可求得
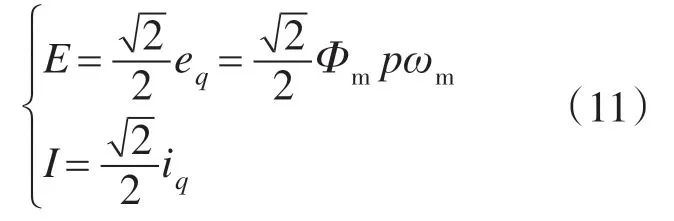
因为永磁感应磁通Φm和极对数p的取值为常数,所以E与ω具有线性关系。然而,在工程中很难直接获得ea的值。不过,工程上很容易获得PMSG 输出端电压ua的有效值U。将式(9)和式(10)带入Pm= Pout/η,可得

将式(12)代入式(11)可求得

假设效率η是一个常量,可知U与ω具有线性关系。在进行MPPT 控制时,可以采用U—P 曲线代替ω—P曲线。这样,在不使用机械传感器的情况下,就可以实现对直驱式风力发电机组的MPPT控制。
根据式(13),将ω—P曲线转换为U—P 曲线。利用U—P 曲线进行MPPT控制的策略可以通过图3来描述。

图3 利用U—P曲线进行MPPT控制的原理图Fig.3 The diagram of MPPT control by using U—P curve
通过对PMSG 的输出端电压和电流进行采样,获得U与I。计算出其输出功率Pout=3UI,然后通过Pm= Pout/η 估算出风力涡轮机的机械功率Pm。
利用U—P 曲线获得Pm,opt。比较Pm,opt和Pm。若Pm,opt>Pm,认为发电机转速过高,则需要减小ωm;反之,需要增大ωm。通过对ωm的调整最终使得Pm,opt≈Pm。因此,根据Pm,opt与Pm的关系来获得ωm的变化量Δωm,将Δωm输入到PMSG 控制器实现对风力发电机组转速的控制[17]。
3 实验结果
3.1 仿真验证
基于小型风力涡轮机的参数构建其Matlab仿真模型。考虑风速随机变化的情况,分别使用U—P 曲线和ω—P 曲线控制策略对SWT 进行MPPT 控制,验证它们的控制效果是否一致。在仿真实验过程中,给定的风速随时间t变化曲线如图4所示。
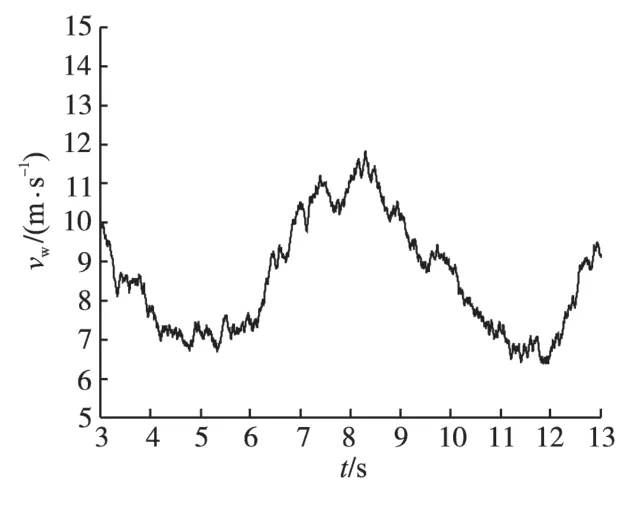
图4 风速变化曲线Fig.4 The curve of wind speed
假设SWT 的效率η = 0.95,所获得的结果分别如图5和图6所示。

图5 PMSG的转子角速度比较.Fig.5 The comparison of the rotor speed of PMSG

图6 PMSG的输出功率比较Fig.6 The comparison of the output power of PMSG
图5中,点划线表示所期望的最优角速度ωopt;虚线表示利用ω—P曲线控制策略进行MPPT控制得到的角速度ωm’ω-P;实线表示利用U—P 曲线控制策略进行MPPT 控制得到的角速度ωm,u-P。图6 中,虚线表示用ω—P曲线控制策略进行MPPT控制得到的PMSG输出功率Pout’ω-P;实线表示利用U—P 曲线控制策略进行MPPT控制得到的PMSG输出功率Pout’u-P。
从图4~图6 可以看出,在随机风速下,分别使用ω—P曲线和U—P 曲线控制策略对SWT 进行MPPT控制,所得到ωm和Pout的结果非常一致。
3.2 实验验证
为了进一步验证本文所提出的控制方法的有效性,构建了采用一个7.5 kW的永磁同步电动机模拟风力涡轮机,来直接驱动一个2 kW的PMSG的实验系统。其中,PMW整流器采用的是IGBT模块CM50TF-12H,控制算法采用TMS320C2812 DSP控制板实现。考虑到模拟风速的随机性比较困难,在试验中测试了一种较为极端的情况,假设风速是阶跃性突变的,对应于驱动电机的转速变化是从200 r/min变化到300 r/min,保持一段时间再恢复到200 r/min。具体实验结果如图7 和图8所示。

图7 PMSG的转子角速度比较Fig.7 The comparison of the rotor speed of PMSG
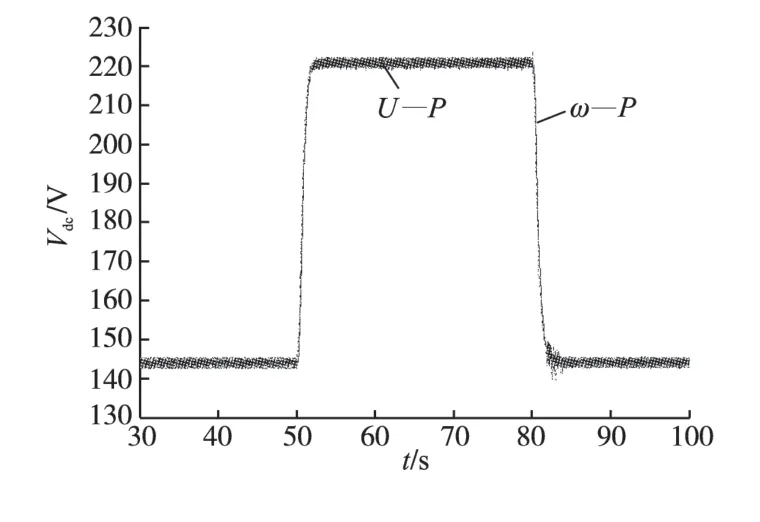
图8 整流器输出电压Vdc比较Fig.8 The comparison of the Vdc
从图7 和图8 可以看出,分别使用ω—P曲线控制策略和U—P 曲线控制策略对SWT 进行MPPT 控制,所得到ωm和Vdc的实验结果非常一致。由于U—P 曲线控制策略不使用机械传感器,所以U—P 曲线控制策略可以简化SWT 控制系统的硬件配置、降低成本和提高系统整体的可靠性。
4 结论
1)本文建立了由风力涡轮机和PMSG组成的SWT的整体数学模型,从理论上分析了采用U—P 曲线控制策略对SWT 进行了MPPT 控制的可行性,并进行了基于U—P 曲线的SWT控制器设计。
2)仿真实验结果说明,使用ω—P曲线控制策略对SWT 进行MPPT 控制可以取得与U—P 曲线控制策略一致的控制效果。
3)通过测量PMSG 输出端电压和电流可以获得U—P 曲线,采用U—P 曲线控制策略不使用任何机械传感器,不仅具有可靠性高和控制成本低的优点,而且具有工程实用性。
[1]Ahmed F Zobaa,Ramesh C Bansal. Handbook of Renewable Energy Technology[M].World Scientific,2011.
[2]Burton T,Jenkins N,Sharpe D,et al. Wind Energy Handbook[M].John Wiley&Sons,2011.
[3]Colak I,Sagiroglu S,Yesilbudak M. Data Mining and Wind Power Prediction:a Literature Review[J].Renewable Energy,2012,46(10):241-247.
[4]Andoni Urtasun*,Pablo Sanchis,Idoia San Martín,et al.Modeling of Small Wind Turbines Based on PMSG with Diode Bridge for Sensorless Maximum Power Tracking[J]. Renewable Energy,2013,55(7):138-149.
[5]祁和生,姚修伟,李德孚,2013 年中小型风能行业发展形势报告[J].中小型风能设备与应用,2014,9(3):15-21.
[6]张小莲,殷明慧,周连俊,等,风电机组最大功率点跟踪控制的影响因素分析[J],电力系统自动化,2013,37(22):15-21.
[7]Rubi Garcia-hernandez,Raul Garduno-ramirez. Modeling a Wind Turbine Synchronous Generator Based on PMSG with Diode Bridge for Sensorless Maximum Power Tracking[J].International Journal of Energy and Power,2013,2(3):64-70.
[8]Kesraoui M,Korichi N,Belkadi A. Maximum Power Point Tracker of Wind Energy Conversion System[J].Renewable Energy 2010,36(10):2655-2662.
[9]Wang H,Nayar C,Su J,et al. Control and Interfacing of a Grid-connected Small-scale Wind Turbine Generator[J].IEEE Transactions on Energy Conversion,2011,26(2):428-434.
[10]Narayana M,Putrus GA,Jovanovic M,et al. Generic Maximum Power Point Tracking Controller for Small-scale Wind Turbines[J].Renewable Energy,2012,44(8):72-79.
[11]张建忠,程明.基于非线性控制的永磁风力发电机最大风能跟踪[J].电网技术,2010,34(6):181-185.
[12]姚骏,廖勇,瞿兴鸿,等.直驱永磁同步风力发电机的最佳风能跟踪控制[J].电网技术,2008,32(10):11-15.
[13]刘向向,李新宇.变结构控制策略在直驱永磁同步风力发电机中的应用[J].电网技术,2013,37(2):520-525.
[14]Serban I,Marinescu C.A Sensorless Control Method for Variable Speed Small Wind Turbines[J].Renewable Energy,2012,43(7):256-266.
[15]殷明慧,张小莲,叶星,等.一种基于收缩跟踪区间的改进最大功率点跟踪控制[J].中国电机工程学报,2012,32(27):24-31.
[16]Dehghan SM,Mohamadian M,Varjani AY. A New Variable-Speed Wind Energy Conversion System Using Permanentmagnet Synchronous Generator and Z-source Inverter[J].IEEE Transactions on Energy Conversion,2009,24(3):714-724.
[17]尹明,李庚银,张建成,等.直驱式永磁同步风力发电机组建模及其控制策略[J].电网技术,2007,31(15):61-65.
