三电平NPC整流器新型直接功率控制策略

李宁，王跃，王兆安，张辉

（1.西安理工大学自动化与信息工程学院，陕西西安710048；2.西安交通大学电气工程学院，陕西西安710049）

电压型三电平中点钳位（NPC）整流器是目前最常用的多电平整流器［1］，相比于传统的两电平整流器，三电平整流器具有输出功率大、输出波形THD 小、器件电压应力和系统EMI 低等多方面的优点，因而被广泛地应用于各种中高压大功率场合［2-3］。

高性能控制策略是三电平NPC整流器的研究热点。目前，最常用的控制策略是电压定向控制（VOC）策略。1991年，Ohnishi T教授提出了直接功率控制策略（DPC）［4-10］。与VOC策略相比，DPC策略直接选择合适的矢量实现对瞬时功率的控制，因而具有算法简单、动态响应更好等优点［11-17］。然而，由于三电平NPC整流器的特殊性及矢量复杂性，DPC策略的应用远不如VOC策略广泛。

本文分析了三电平NPC 整流器DPC 策略的基本原理，推导了其数学模型，提出了一种无需交流电压传感器的三电平DPC策略，该策略通过系统其他参数估计瞬时功率，节省了硬件成本。在三电平NPC整流器中，直流电容电压波动也是一个亟待解决的问题，本文通过合理选择矢量选择表中各矢量对应的开关状态解决了三电平NPC整流器存在直流电容电压不平衡问题。最后，通过仿真和实验对本文的理论分析进行了验证。

1 三电平NPC整流器数学模型

图1 所示为三电平NPC 整流器等效电路图。图1 中，每相桥臂的电路结构可以简化为一个与直流侧电容相通的单刀三掷开关。在图1中，N 为其参考点；Rs，Ls分别为线路等效电阻和网侧电感；ux（x=a，b，c）为电网相电压，ix为三相电流；Sx为开关函数，Sx=Sxy（y=p，o，n）时x相输出y电平；C1，C2为直流电容（C1=C2=C），uc1和uc2为两电容上电压；ip和in分别为流入p点和n点的电流，ic1和ic2为流过直流电容的电流；LL和RL为负载侧等效电感和电阻，iL为负载电流。

图1 三电平NPC整流器主电路拓扑等效图Fig.1 Equivalent circuit of three-level NPC rectifier

将图1 中各量变换到两相同步旋转坐标系中，可得整流器的数学模型为

式中：ud，uq，id，iq分别为三相电压ux和ix（x=a，b，c）在同步旋转坐标系中的对应值；Sdy，Sqy分别为开关函数Sxy（x=a，b，c，y=p，n）在d，q轴上的对应值。

根据瞬时无功功率理论［4-6］，三相电路瞬时功率为

式中：ud，uq为电网电压的d，q轴分量。

当d轴始终与参考电压矢量重合时，ud=0，此时瞬时功率的表达式为

由式（1），系统电压电流满足如下约束：

式中：ω为同步旋转坐标系的角速度；θ 为旋转坐标系转过的角度，θ=ωt。

将上式的左右两边同乘以ud，并结合式（3）有：

定义参考电压矢量在z轴上的投影urd和urq如下：

实际应用中一般忽略Rs项的影响，且考虑ud幅值与相电压有效值U的关系有：

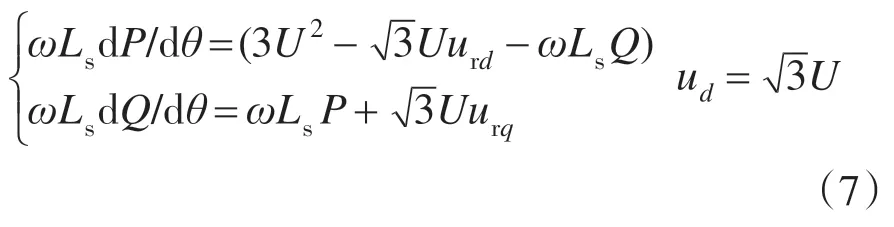
实际中为了简化分析难度，往往忽略式（7）中的耦合项［9-10，17］，则有：

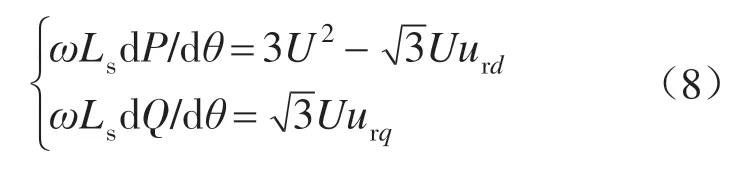
2 新型三电平DPC策略

图2 为三电平NPC 整流器新型DPC 系统控制框图。其中，瞬时功率估算、开关状态选择表及直流电容电压均衡策略是核心部分。

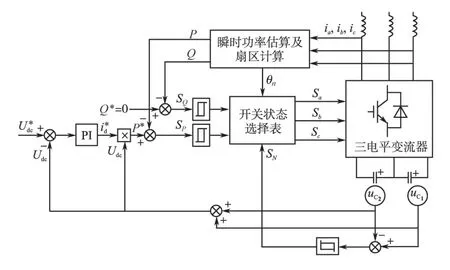
图2 三电平NPC整流器DPC系统结构图Fig.2 Block scheme of three-level NPC DPC system

2.1 新型三电平DPC策略瞬时功率的估算

根据图2和基尔霍夫定律，可得到如下等式：

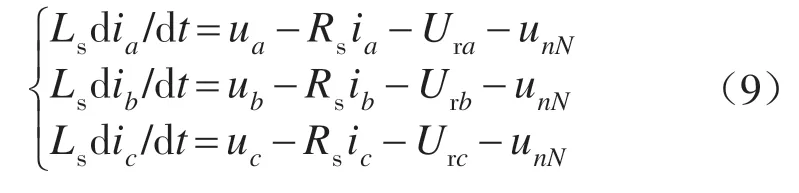
式中：Ura，Urb，Urc分别为三相整流器输入侧相对于直流侧n点的电压。

根据三相整流器的控制规律，有：

式中：Sx为x相的开关状态；Udc为直流总电压。

设unN为直流侧n 点相对于交流侧N 点的电压。根据式（8）和ia+ib+ic=0，则有：

若三相电压对称，则有：

将式（10）带入式（9）整理有：

根据式（11），可用等式的右边的值来计算左边的值，进而得到DPC 策略瞬时功率估算公式：

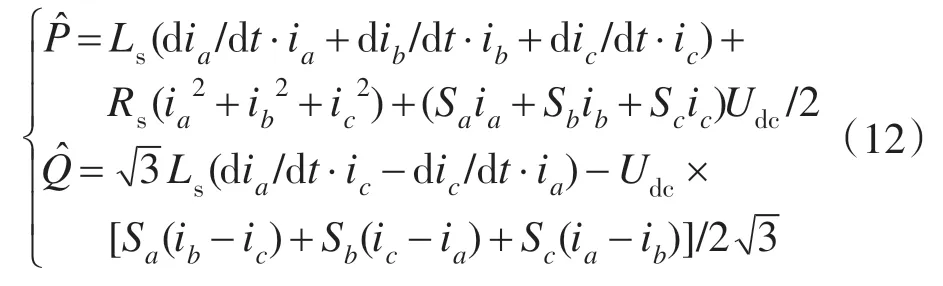
2.2 新型三电平DPC策略的开关状态选择表

图3a 所示为NPC 型三电平整流器空间电压矢量分布图。为了分析各矢量对瞬时功率的影响，将整个空间矢量图分为12个扇区（θ1～θ12），具体如图3b 所示，本文中将编号为奇数的扇区称为奇数扇区，编号为偶数的扇区称为偶数扇区。

图3 三电平NPC整流器电压矢量及DPC策略扇区划分Fig.3 Vectors and sector division of three-level DPC system

在DPC 策略的矢量选择中本文做如下的设定：为了减小系统的损耗，降低du/dt，优先选择参考电压矢量所在大扇区（相邻大矢量围成三角形）中距参考矢量最近的合适矢量。如当参考电压矢量落在第1，2 扇区时，先考虑由V01，VL1，VL2构成三角形中合适矢量。根据图3中各矢量的长度及式（8），结合本文的设定，可得如表1 所示三电平DPC策略矢量选择表。

表1 三电平NPC整流器DPC策略矢量选择表Tab.1 Vector selection table of DPC strategy

表1中，VS（j+1）/（j-5）表示当j+1≤6时选VS（j+1），否则选VS（j-5），其它矢量同理。SP，SQ表示给定功率与实际瞬时功率比较后得到开关信号；SP，SQ的计算公式如下式所示：

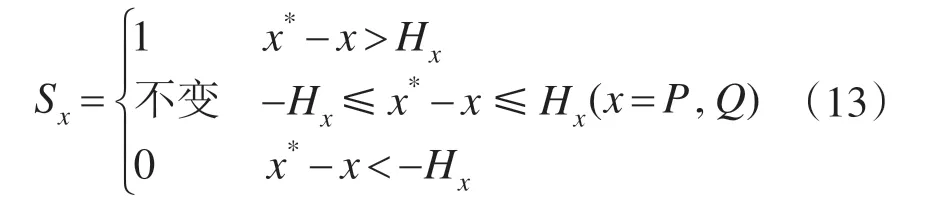
式中：Hx为瞬时功率滞环宽度。

2.3 三电平NPC整流器DPC策略中直流电容电压的平衡控制

两电容器之间的电压均衡问题是NPC 型拓扑的固有问题。在NPC 型三电平整流器DPC 策略中，系统矢量选择表（表1）给出的是满足功率变化需要的矢量，而不是直接选择开关状态，在图3b中，小矢量和中矢量会对中点电压的平衡产生影响，而每个小矢量对应2个开关状态，这2个开关状态会产生反方向的中点电流，故可以通过合理选择小矢量的开关状态来平衡中点电压。

由图1可以得到中点电流io的表达式如下：

据此，可以定义：

根据式（15）和表1，当选择表1 中的小矢量时，根据电流方向合理的选择小矢量对应的开关状态，就可以实现中点电压的平衡控制，小矢量开关状态选择如表2所示，其中I表征与小矢量对应的相电流，其具体表达式如下：

表2 电容电压平衡的三电平DPC系统开关状态选择表Tab.2 Switching states selection of three-level DPC system

3 仿真和实验验证

为验证本文的分析，搭建了三电平NPC整流器仿真和实验平台对其进行验证。系统主电路如图1所示，控制框图如图2所示，平台系统主要参数为：交流侧线电压有效值170 V，直流母线电压Udc=300 V，Ls=6 mH，C1=C2=1 000µF，额定功率2.5 kW，瞬时功率滞环宽度HP=HQ=25 W（var），直流电容电压滞环宽度Hu=5 V。

如图4 所示为采用本文提出的新型三电平DPC 策略的仿真结果。初始时刻给定有功功率为1 250 W，无功功率为0 W，在0.1 s 末有功功率跳变为2 500 W。三电平NPC 整流器瞬时功率P 和Q、直流电容电压Uc1和Uc2、输出电压脉冲Uab和Uc及网侧电压ua和电流ia的波形在图4中给出。由图4 可知，本文提出的新型三电平DPC 策略在不采用交流侧电压传感器的前提下具有动态性能好，对系统瞬时功率的控制效果较好的特点。

图4 三电平NPC整流器DPC策略仿真结果Fig.4 Simulation results of three-level NPC DPC system

如图5 所示为采用本文提出的新型三电平DPC策略的实验结果，设定系统输出有功功率为2 500 W，无功功率为0 var。图5中给出了三电平NPC整流器瞬时有功功率变化量ΔP和瞬时无功功率变化量ΔQ，直流总电压Udc和电容电压Uc1，变流器输出线电压脉冲Ubc和Ua，网侧线电压ubc电流ia的波形。实际系统受采样精度、器件散热工艺、驱动电路功率等多方面因素的影响，其器件平均开关频率较低，因而实验结果与仿真结果在定量比较方面有一定差异。对比图4和图5可以发现，仿真结果和实验结果从性质上完全相符。通过理论分析、仿真和实验表明本文提出的新型三电平DPC策略确实具有较好的控制效果。

图5 三电平NPC整流器DPC策略实验结果Fig.5 Experiment results of DPC system

4 结论

本文分析了三电平DPC 策略原理，推导了其数学模型，在此基础上提出了一类新颖的无交流电压传感器的三电平NPC 整流器DPC 策略。该策略实现简单，可以充分节约系统硬件和软件成本，同时可以消除直流电容电压不平衡这一NPC 拓扑的固有问题，这些都将大大增加NPC型变流器的应用前景与市场竞争力。当然，本文提出的DPC 策略也存在一定的不足之处，比如系统开关频率不固定，这为硬件电路的设计增大了难度。

［1］Nabae A，Takahashi I，Akagi H. A New Neutral Point Clamped PWM Inverter［J］.IEEE Transaction on Industry Applications，1981，17（5）：518-523.

［2］张兴.PWM 整流器及其控制策略的研究［D］.合肥：合肥工业大学，2003：5-20.

［3］Franquelo L G，Rodriguez J，Leon J I，et al.The Age of Multilevel Converters Arrives［J］. IEEE Transactions on Industrial Electronics，2008，2（2）：28-39.

［4］Akagi H，Kanazawa Y，Nabae A.Instantaneous Reactive Power Compensators Comprising Switching Devices Without Energy Storage Components［J］. IEEE Trans. on Industry Application，1984，20（3）：625-630.

［5］Peng F Z，Lai J S. Generalized Instantaneous Reactive Power Theory for Three-phase Power Systems［J］.IEEE Transactions on Instrumentation and Measurement，1996，45（1）：293-297.

［6］刘进军，王兆安. 瞬时无功功率与传统功率理论的统一数学描述及物理意义［J］. 电工技术学报，1998，13（6）：6-12.

［7］Takahashi I，Noguchi T. A New Quick-response and Highef fciency Control Strategy of an Induction Motor［J］.IEEE Transactions on Industry Applications，1986，22（5）：820-827.

［8］Depenbrock M. Direct Self-control（DSC）of Inverter-fed Induction Machine［J］. IEEE Transactions on Power Electronics，1988，3（4）：420-429.

［9］Ohnishi T. Three Phase PWM Converter/inverter by Means of Instantaneous Active and Reactive Power control［C］//International Conference on Industrial Electrlnics，Control and Instrumentation，1991：819-824.

［10］Noguchi T，Tomiki H，Kondo S，et al．Direct Power Control of PWM Converter Without Power-source Voltage Sensors［J］. IEEE Transactions on Industry Applications，1998，34（3）：473-479.

［11］杨达亮，卢子广，杭乃善，等.三相电压型PWM整流器准定频直接功率控制［J］.中国电机工程学报，2011，31（27）：66-73.

［12］李爽，王志新，王国强.海上风电柔性直流输电变流器P-DPC 控制研究［J］. 电工技术学报，2013，28（2）：264-269.

［13］韩愚拙，林明耀，郝立，等.电压型PWM整流器三状态直接功率控制策略［J］.电工技术学报，2013，28（5）：208-211.

［14］张永昌，谢伟，李正熙.PWM 整流器功率脉动最小化方法的研究［J］.中国电机工程学报，2013，33（18）：57-64.

［15］张颖超，赵争鸣，鲁挺，等.固定开关频率三电平PWM 整流器直接功率控制［J］.电工技术学报，2008，23（6）：72-77.

［16］鲁挺，赵争鸣，张颖超，等.采样延迟和误差对三电平PWM整流直接功率控制性能的影响及其抑制方法［J］.电工技术学报，2010，25（3）：66-72

［17］张颖超，赵争鸣，袁立强，等.三电平PWM整流器直接功率控制［J］.电工技术学报，2008，23（5）：62-68.