单位功率因数与重复预测在APF中的应用

王梦琼，许春雨

（太原理工大学电气与动力工程学院，山西太原030024）

1 引言

随着电力电子装置的广泛应用，电网中的谐波问题日益严重。如何准确、实时地检测及补偿电网畸变电流谐波分量是决定有源电力滤波器（APF）性能的重要环节［1］。

本文研究三相并联型有源电力滤波器，谐波检测采用单位功率因数（UPF）检测法，APF 补偿后，电源侧电流与电网电压同频同相。该方法算法简单、精度高，单相系统、三相三线制系统、三相4线制系统均适用。

电流跟踪控制采用电压空间矢量PWM（SVPWM）控制方法，其本身存在一拍滞后，因此在SVPWM 中加入电流预测来实现无差拍控制效果。

2 单位功率因数检测法

UPF谐波电流检测法采用等效原理，将非线性负载和APF整体视为电阻性负载，这样补偿后电源电流与电网电压波形相同，功率因数为1（单位功率因数）。

公用电网中，通常电压波形的畸变很小，而电流波形畸变可能很大，所以一般不考虑电压畸变，研究电压波形为正弦波、电流波形为非正弦波的情况有很大的实际意义［2］。因此假设电网电压三相平衡无畸变，其傅里叶展开式为

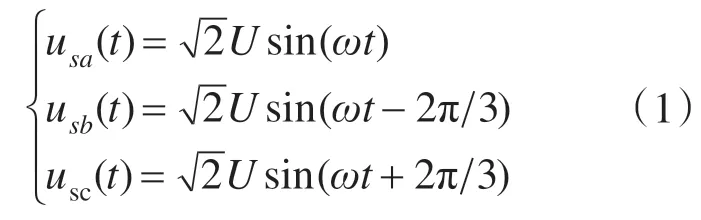
根据UPF检测法，补偿后电源电流可表示为

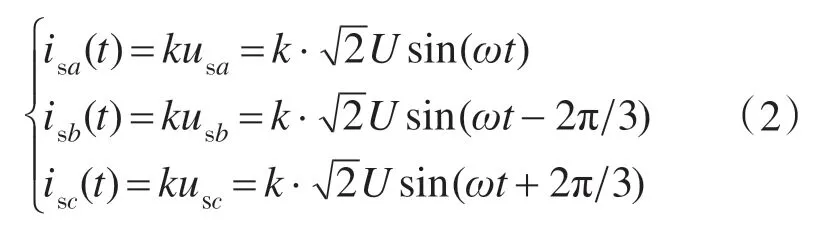
式中：usa，usb，usc为三相电源电压；isa，isb，isc为三相电源电流；k为非线性负载和APF 并联的等效复合负载电导。

负载电流傅里叶展开式为

式中：iL(t)为负载电流，即补偿前电源电流；is(t)为补偿后电源电流；iq(t)为谐波及无功电流和。

由于功率因数为1，iq(t)不产生有功功率，所以有：

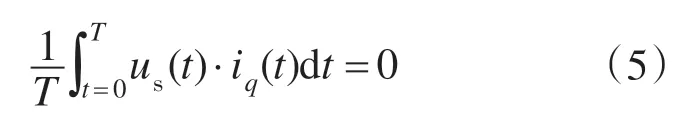
把式（4）代入上式，可得：

对于三相系统，可知：

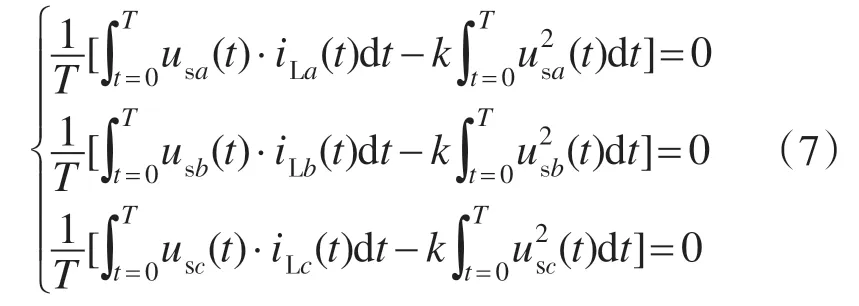
式（7）中3式左右相加化简，得：

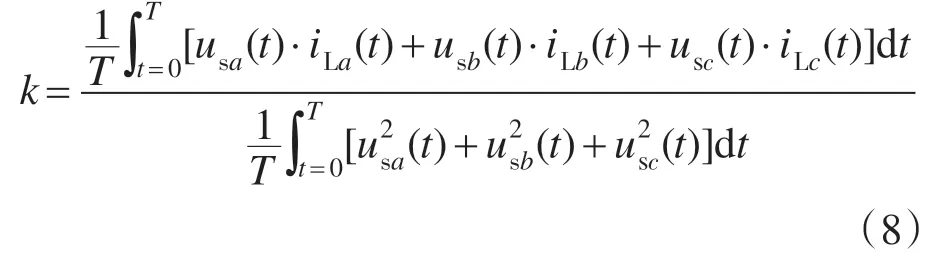
usiiLi和在一个周期内的积分值分别为其直流分量与积分周期的乘积，所以有：

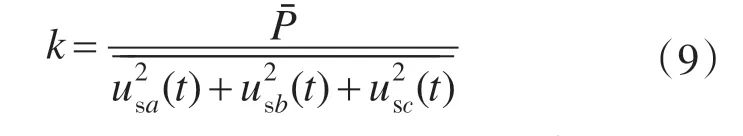
通过低通滤波器可提取到三相功率之和与电压平方和的直流分量［3-5］。根据式（9）确定等效复合负载电导k，由式（4）可得谐波及无功电流和，即补偿电流：

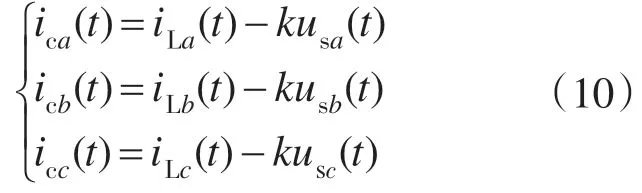
由式（10）可知，若电网电压us发生畸变，则检测出的补偿电流ic会随之产生畸变，降低APF 补偿效果。因此引入锁相环PLL，由锁相倍频电路检测A 相电压过零点并复位查正弦表，提取电网电压的基波分量，这样kus就为负载电流的基波分量，检测出的谐波及无功电流不会受电网电压畸变的影响。

图1 为加入锁相环的UPF 谐波检测框图。

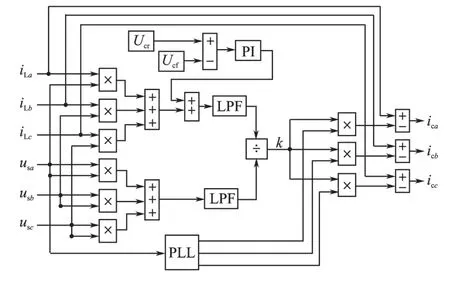
图1 加入锁相环的UPF谐波检测框图Fig.1 Block diagram of UPF detection with PLL

3 电流预测

SVPWM 基于交流电机磁场理论，依靠开关器件通断的控制，使其输出电压逼近期望输出电压。该方法在k时刻涉及k+1 时刻的补偿电流ic（k+1），一般可用指令电流代替，但这样就存在一拍滞后。本文采用的基于SVPWM 的无差拍控制方法，在k时刻预测下一时刻的指令电流值用以代替ic（k+1），消除滞后影响，实现实时控制。是否能实时、准确地预测出k+1 时刻补偿电流是实现无差拍控制效果的关键［6-8］。

常用预测方法有：线性预测、抛物线预测、重复预测、神经元预测和自适应预测等。后两种方法计算复杂，运算量大，实时性不好。

线性预测可表示为

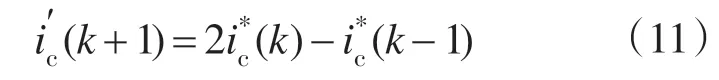
抛物线预测可表示为

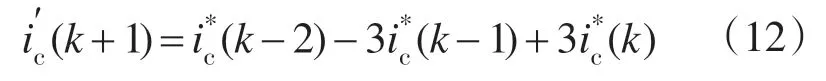
文中采用重复预测观测器进行指令电流的预测。利用当前时刻指令电流与实际指令电流的预测误差，与比例系数相乘作为补偿量，叠加到指令电流实际采样值。k时刻的误差计算公式为

采样次数为N，每个采样点均设置相应误差存储单元e（k），k∈［1，N］。

在负载稳定的情况下，前一基波周期的预测误差e（k）与k2的乘积，加上k时刻得到指令电流采样值即图2中A取，就可得到k+1时刻的指令电流预测值，其表达式为

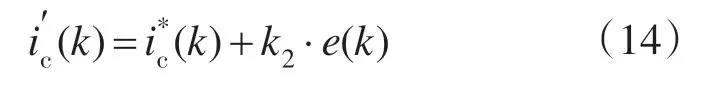
当系统负载突变时，谐波电流随负载突变，为提高这种暂态情况下的滤波精度及动态性能，可以进一步采用拉格朗日插值法来逼近实际值。即此时可取：

或

重复预测结构框图如图2所示。

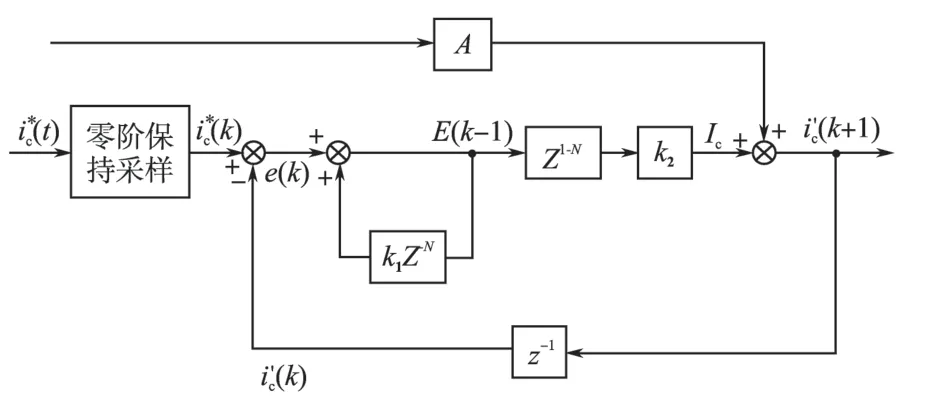
图2 重复预测结构框图Fig.2 Block diagram of repetitive predictor

得

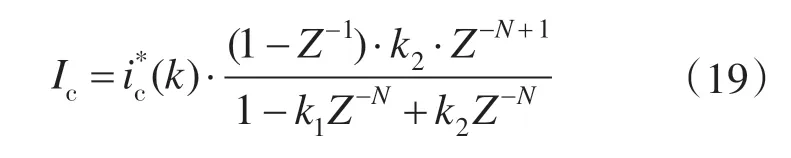
因此可以得出重复预测型电流误差的传递函数为

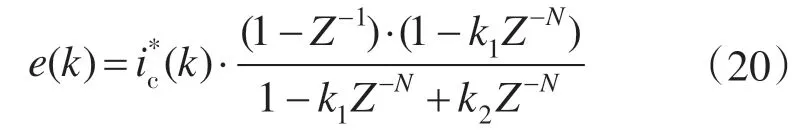
等效为误差输出的形式如图3所示。

图3 误差输出等效模型Fig.3 Equivalent model of error output

有源滤波器的稳定工作需保证重复预测能够准确预测指令电流值，即预测误差要收敛于0。由小增益定理可知，系统稳定的条件是系统的闭环极点在单位圆内，即反馈回路开环传递函数增益恒小于1。对（k2-k1）Z-N，进行z=ejωTs代换，可以得到重复预测观测器稳定的充分条件为

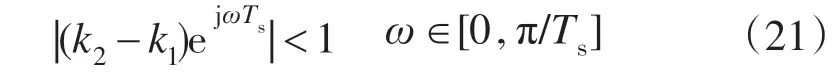
由式（21）可知，只要令|（k2-k1）|＜1，重复预测观测器就能稳定。但在实际系统中，由于各种因素的影响，即使在稳态情况下，谐波电流也不可能与上一周期的波形完全一致，总会出现或大或小的变化。为此周期积分环节系数k1设置为0.95，削弱积分作用，避免因不能完全消除预测误差而导致补偿量无限制增加。比例系数k2适当取小也可减少补偿量，使校正作用更平缓，所以k2取0.98［10］。

4 Matlab仿真分析

图4所示为Matlab/Simulink环境下搭建的三相并联型APF仿真模型。

图4 三相并联型APF仿真模型Fig.4 Simulation model of three-phase shunt APF

APF仿真参数为：三相对称电源220 V，50 Hz；三相二极管整流桥带电阻负载，进线电感1 mH；直流侧电容1 100 μF，参考电压1 000 V，初始电压1 000 V；交流侧电感8 mH。

1）负载稳定。电阻恒为30 Ω。

图5所示为A相电流波形及其FFT分析。由图5 可知，A 相负载电流谐波总畸变率高达27.62%，不加重复预测时补偿后电源电流谐波总畸变率为6.24%，采用重复预测观测器进行APF补偿后A相电源电流中绝大部分谐波和无功成分被消除，其谐波总畸变率降为1.98%，且动态响应时间小于1个周期。

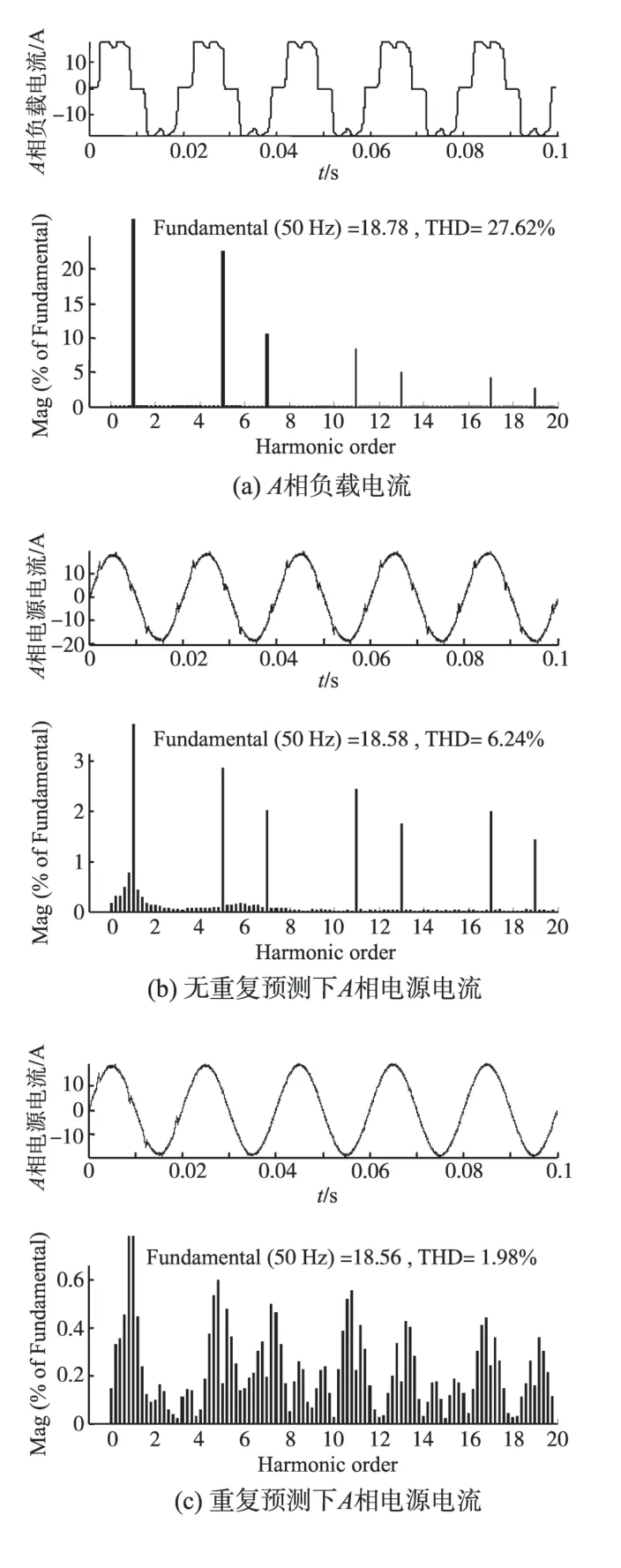
图5 负载稳定时A相电流波形及其FFT分析Fig.5 Waveforms and FFT analysis of A-phase current under the stable load

2）负载突变情况。0.06 s 时并入1 个30 Ω电阻，使负载电阻突减。A 相电流波形及其FFT 分析如图6所示。

由图6 可知，在0.06 s 负载突变后，经过一个周期谐波电流即可得到跟踪补偿。可见采用基于SVPWM 的无差拍控制方法能有效地控制APF补偿电流。

图6 负载突变时A相电流波形及其FFT分析Fig.6 Waveforms and FFT analysis of A-phase current under the load changing suddenly

5 实验验证

实验装置系统结构如图7所示。三相负载为带电阻负载的三相不可控整流桥。整流桥采用东芝公司的30Q6P42 模块，示波器采用安捷伦54621D。

图7 APF实验装置系统结构Fig.7 APF experimental device system structure

实验参数为：线电压40 V，整流桥负载电阻30 Ω，交流侧电感8 mH，直流侧电容电压给定值90 V，直流侧电容2 200 μF。

图8 所示为实验波形，图8 中可以看出补偿后电源电流接近正弦波，谐波得到了有效抑制。

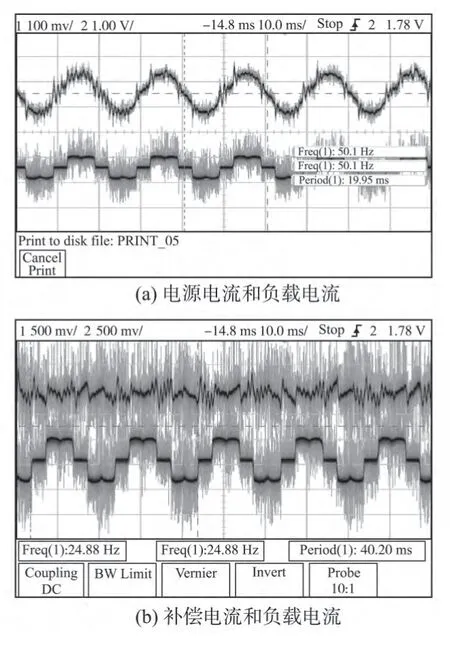
图8 补偿后实验波形Fig.8 Experiment waveform after compensation

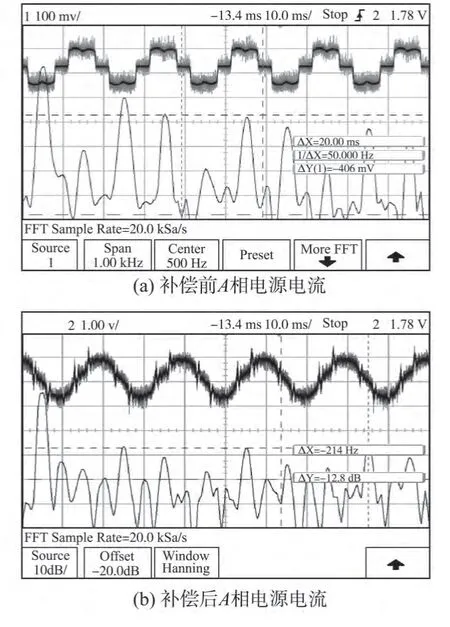
图9 补偿前后A相电源电流波形及其FFT分析Fig.9 A-phase supply current and FFT analysis before and after compensation

图9所示为补偿前后电源电流波形及其FFT分析。由负载电流和电源电流的基波分量及各次谐波分量有效测量值，可根据下式计算得到补偿前后各次谐波电流含有率：

其主要次（6k±1）谐波百分含量分析见表1。

实验结果可以看出，20次以内的谐波都得到了抑制，其中5次和7次谐波的抑制效果最明显，17 次和19 次效果较差。因此该有源电力滤波器能够补偿电网主要次谐波，单位功率因数谐波检测法与空间电压矢量跟踪控制方式在APF 中应用的可行性得到了验证。

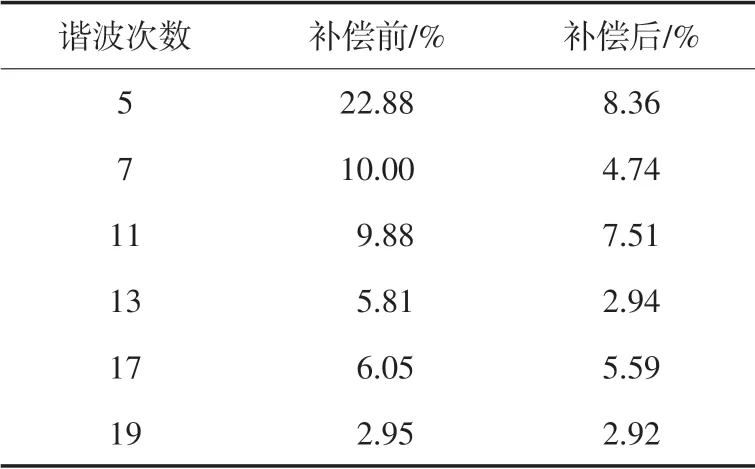
表1 补偿前后各次谐波电流含量Tab.1 The harmonic content before and after compensation

6 结论

本文介绍了单位功率因数电流检测算法，以及基于重复预测的空间矢量脉冲调制无差拍控制策略。分别分析了其基本思路，并在仿真环境和低压实验条件下进行实验验证。结果表明本文所采用的方法具有可行性和有效性。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.北京：机械工业出版，1998.

［2］王兆安，刘进军.电力电子技术［M］.北京：机械工业出版，2009.

［3］张红莲，袁兆强.基于单位功率因数的谐波和无功电流实时检测方法［J］.电力自动化设备，2006，26（2）：37-39.

［4］赵怀军，庞亚飞，邱宗明，等.改进的单位功率因数谐波电流实时检测方法［J］.电网技术，2007，31（9）：38-42.

［5］María Isabel Milanés Montero. Comparison of Control Strategies for Shunt Active Power Filters in Three-phase Four-wire Systems［J］.IEEE Trans. on Power Electronics，2007，22（1）：229-236.

［6］管恩振，王志和，张晓新.空间矢量控制方法在并联型有源电力滤波器中的应用研究［J］.内蒙古工业大学学报，2005，24（2）：86-90.

［7］杜永，任贤贤，高思远.供电系统中的谐波和无功补偿技术［J］.煤炭工程，2013，45（10）：83-85.

［8］王妍，杜军红，陶伟宜，等.基于DSP 的空间电压矢量法PWM的研究［J］.电机与控制学报，2000，4（2）：98-101，105.

［9］唐健，王翔，何英杰，等.三相四线制有源滤波器的新型无差拍控制［J］.电力系统自动化，2007，31（19）：59-63.

［10］张国荣，邵竹星，陈林.基于改进重复预测原理的并联有源电力滤波器无差拍控制策略［J］.农业工程学报，2012，28（13）：172-178.