异步电机电感参数的离线辨识

候春辉，单亚飞，李峰，王曦冉

（天津大学电气与自动化工程学院，天津300072）

1 引言

在工业控制中，对交流调速系统的性能需求越来越高，这使得矢量控制、直接转矩控制等一些高性能的调速理论广泛地应用于实际调速系统之中［1-2］。但矢量控制、直接转矩控制调速性能的优劣都与电机参数有密切的关系，因此，获得精确的电机参数是实现电机矢量控制、直接转矩控制及无速度传感器控制的关键。传统获得电机参数的方法主要是对电机做堵转试验和空载试验［2］，但是这种手动操作的电机测试方法存在着测量时间不同步、人为因素影响大、工作效率低等缺点［3］。因此，人们提出了各种离线辨识的方法来检测电机参数，现有辨识方法，主要是基于注入信号的方法来获得电机相应的响应。本文在已有的异步电机调速平台上，通过DSP控制逆变器产生特定的PWM电压作为激励加在电机上，对电机进行脉冲实验和单相交流试验，在这些特殊信号的激励下，电机的等效电路可以得到简化，通过检测电机定子电流，再经过基于DSP运算处理单元的软件运算，便可以实现对电机电感参数的辨识。

2 异步电机的等效电路

电机学中常用的异步电机等效电路为T型等效电路，如图1所示，其特点是忽略铁耗。图1中Rs，Lsl分别为定子电阻和漏感；Rr，Lrl分别为折合到定子侧的转子电阻和漏感；Lm为互感。

图1 异步电机T型等效电路Fig.1 T-form equivalent circuit of asynchronous motor

但是T型等效电路并不是异步电机唯一的等效电路，在理论上，定子侧输入阻抗相同的等效电路应该有无数个。因此通过计算可以把T型等效电路变换成图2 所示的不对称等效电路，该等效电路的特点是励磁电流Im与转子电流Ir正交，称为反Г型等效电路［4］。

图2 异步电机反Г型等效电路Fig.2 Inverse Г-form circuit of asynchronous motor

图2中参数与T型等效电路参数关系如下：

式中：Ls，Lr分别为定子电感和转子电感。

同时Gastli分析了在单相信号激励下T型等效电路和反Г型等效电路在电机参数辨识中的优劣，并得出了后者在相同的激励信号下稳定性优于前者的结论［5］。因此本文采用反Г型等效电路对电动机进行分析。以异步电机A相定子绕组为例，根据反Г型等效电路可以得出电路的矢量表达式。

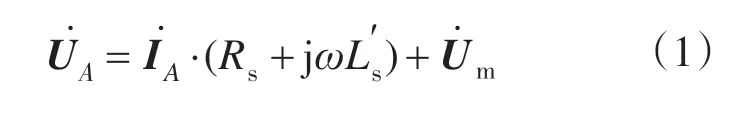
将上式用向量图表示，如图3所示。

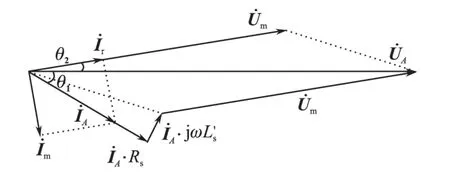
图3 异步电动机反Г型等效电路向量图Fig.3 Vector diagram of inverse Г-form equivalent circuit of asynchronous motor

3 辨识原理

图4是逆变电路驱动异步电机的拓扑图。本文采用的是电压型逆变器，通过控制功率管的通断，可产生需要的电压激励信号。为了使DSP数据处理起来比较简单，本文一直保持B，C相绕组等电势，即B，C 相绕组是短接在一起的，例如在向A 相绕组施加某个电压UA时，B，C 相绕组相应的加-UA/2的电压，根据3/2 变换，这样能保证三相合成的矢量电压始终为3UA/2。且若以此方式向定子三相绕组施加电压，则有Ia=-Ib/2=-Ic/2，只需测量A相电流即可推算出另外两相的电流。

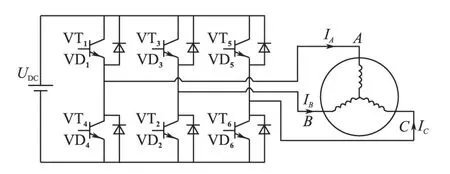
图4 逆变电路驱动异步电机拓扑图Fig.4 Topology of asynchronous motor driven by inverter

定子电阻Rs的辨识一般都是通直流电压根据伏安法利用电压和电流的比值算出来，只是在电压测量时应该考虑逆变器非线性的影响。本文对Rs的辨识不再详述，在认为已经得到Rs的前提下，只考虑对定转子总漏感和互感的辨识。

3.1 定转子总漏感辨识

对图2电路加高频电压时，由式（1）～式（3）可以得出当电压角频率ω足够大时，

将式（2）、式（4）代入式（1）得：

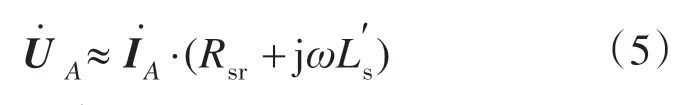
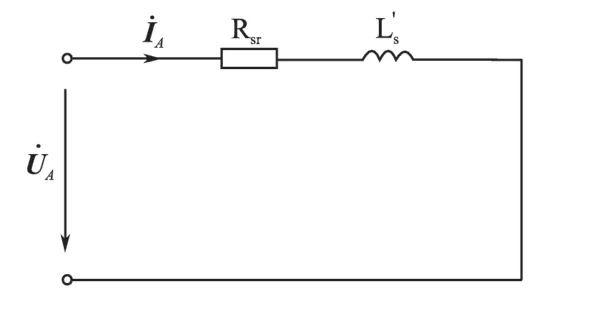
图5 高频下反Г型等效电路的简化电路Fig.5 Simplify circuit of inverse Г-form equivalent circuit under the high frequency

本文中的具体方法是：在电机电流稳定时通高频成分比较重的脉冲电压，此时，励磁电流Im可以忽略，理想情况下，若所加脉冲幅值足够大，

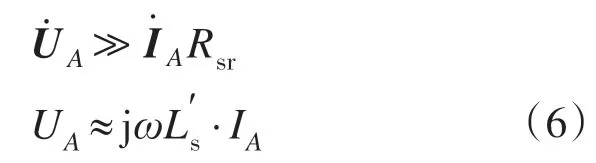
在电流建立的初期，定子电流短暂的上升过程可以认为是线性变化的。如图6所示。

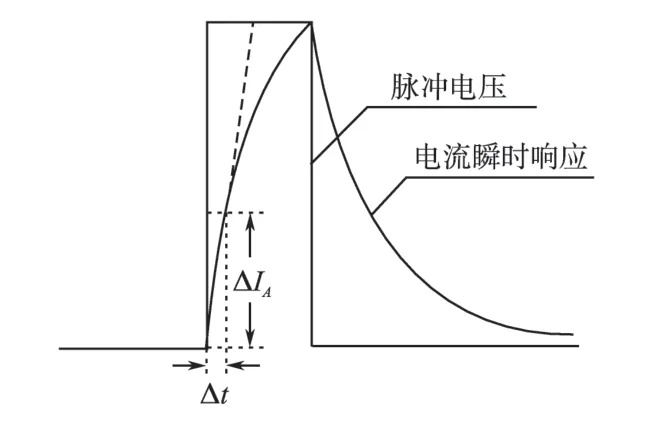
图6 电流脉冲响应示意图Fig.6 Impulse response of current

根据式（6）得：

3.2 互感辨识

在互感辨识时，对异步电机施加单相正弦电压，由于单相电不能使电机产生磁场转矩，电机处于静止状态。采用SPWM调制法，通过脉冲调制，从而在电机的A 相和B，C 两相之间产生正弦电压。根据图3 异步电动机反Г型等效电路向量图，假设，

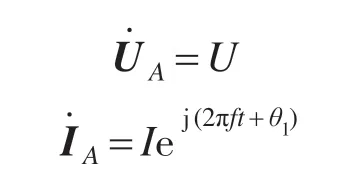
将上面2 个式子代入式（1），由于Rs已知，L′s在前面已经算出，可以求得

假设：

可以计算出：

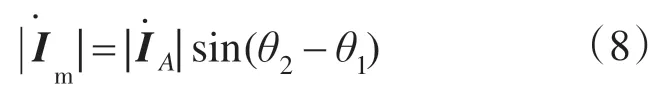
式中：θ1，θ2分别为的相位角，且θ1为负值。

根据式（2）可以算出，

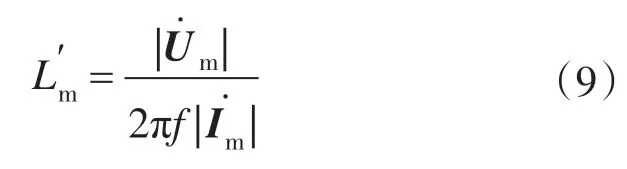
根据异步电机反Г型等效电路也可计算出定子电感：

4 辨识过程中的问题

在实施具体辨识的过程中，还要考虑几个问题：首先是辨识中死区效应对逆变器实际输出电压的影响，如果电压检测不准确，这会直接影响到电机参数辨识结果的精度；其次是所加电压激励信号的幅值频率对辨识结果的影响。

4.1 定子电压补偿

计算时所采用的电压往往采用的是指令参考电压，即利用直流侧电压和PWM 占空比来重构定子电压［6］。

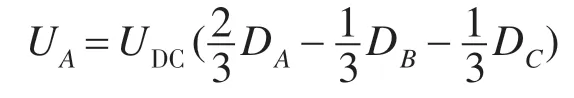
式中：UA为A 相电压；UDC为直流母线电压；DA，DB，DC分别为A，B，C三相理想占空比。

而在实际系统中，考虑到逆变器死区非线性的影响，计算得到的电压与实际逆变器输出的电压会有一定的误差，所以在计算指令参考电压时要考虑死区时间对系统的影响。死区分析波形图如图7所示。

下面是对死区误差电压的分析［7］和补偿方法的介绍。

当ia＞0时，图7a 为上下桥臂理想的通断波形；图7b 为带死区的PWM 波；图7c 为理想输出电压；图7d为考虑死区和功率器件导通关断延时的实际输出电压。同理可分析ia＜0的情况。由图7c、图7d分析可知误差电压，

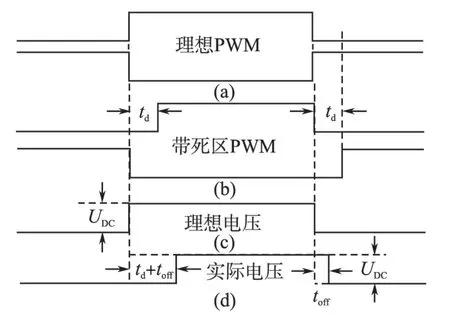
图7 死区分析波形图Fig.7 Analysis waveform of dead zone

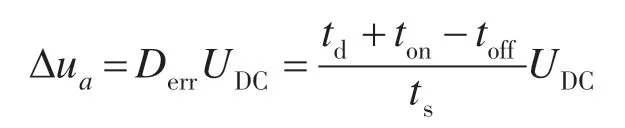
式中：td，ton，toff，ts分别为死区时间，功率管开通、关断时间和一个功率管开关周期。

实际设计中，根据电流的极性确定补偿电压的极性。在指令电压上补偿一个误差电压，便可以抵消误差电压的影响，保证重构电压和实际电压基本一致。

4.2 激励信号的选取

在施加具体的电压激励信号时，需要考虑信号的幅值频率对辨识结果的影响。在对电机施加脉冲信号时，需要考虑脉冲宽度和脉冲幅值。如果脉冲强度太小，电流响应的幅度不够，用此辨识得到的参数会有较大误差，如果脉冲强度太大，则可能会影响电机寿命，甚至会损坏电机。设计中，我们所施加的脉冲激励信号为5个PWM周期，脉冲所激起的最大电流保证在电机额定电流范围之内。对于所施加的单相正弦电流应达到电机额定电流的80%。而正弦电压的频率选取要考虑Im，Ir幅值的关系，设计中选定0.5Ir≤Im≤2Ir，这样能保证Im和IA有足够大的相角，使互感的辨识有足够的测量精度。

5 实验与结果

上述辨识方法在以TI 公司DSP 器件TMS320LF2407A为核心控制器的运动控制平台上得到了验证，实验中PWM 开关频率为2 kHz。异步电机铭牌参数为：额定功率0.37 kW，额定电压400 V，额定电流0.95 A，额定频率50 Hz，额定转速2 800 r/min。由传统的堵转实验、空载实验得到的异步电机参数为：总漏感116.3 mH，互感1.312 H。

5.1 死区补偿结果

由于正弦实验是在低频下进行，实验根据3.1提到的算法只分别测试了A相正弦电压在频率ƒ为0.2 Hz，1 Hz，5 Hz下的死区补偿效果对比实验，图8为上述电压补偿方法补偿前后A相电流波形图。

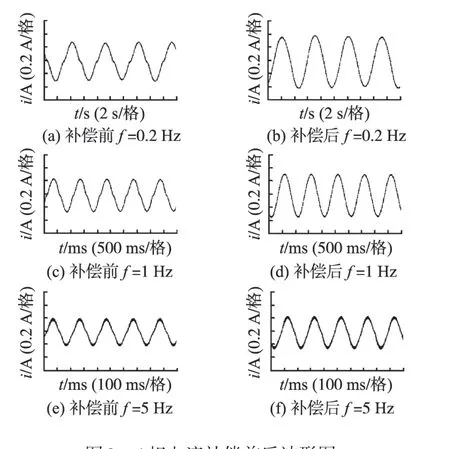
图8 A相电流补偿前后波形图Fig.8 A phase current waveform before and after compensation

所加死区时间为4.8 μs，由图9可以看出补偿基本消除零电流钳位现象。

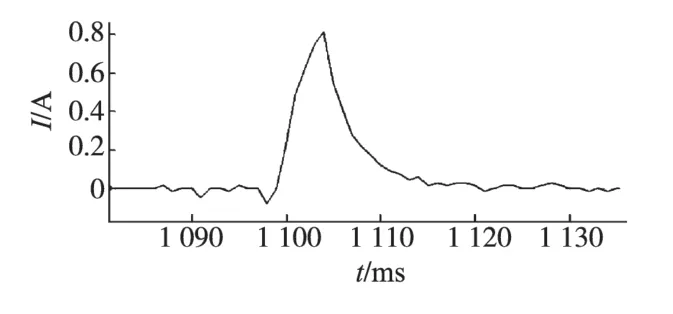
图9 采样电流脉冲响应波形图Fig.9 Impulse response waveform of sampling current

5.2 漏感辨识实验

实验中在电机电流稳定在零时在A相定子绕组施加脉冲电压，经脉冲幅值调整模块调整后脉冲幅值为54 V，脉冲持续5个PWM周期即2.5 ms，脉冲电流最大值约0.8 A。图9为上位机监测到的电流脉冲响应波形；图10为电流脉冲实际响应波形图。图10中下面波形为上面波形的放大图，重复做10 次实验，根据3.1 节算法选取波形的第1个和第3个电流值进行运算，计算得到10个漏感值，然后求取平均值。漏感的辨识结果见表1。

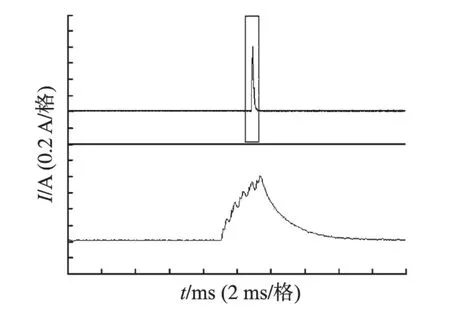
图10 电流脉冲响应图Fig.10 Impulse response of current

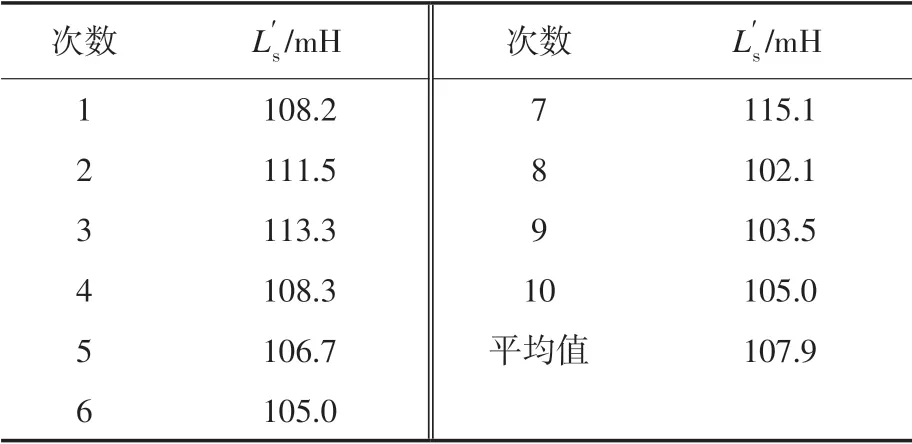
表1 总漏感辨识结果Tab.1 Identification results of total leakage inductance

5.3 互感辨识结果

互感的辨识是在A 相通单相交流电流，经正弦幅值频率调整模块调整后，正弦电流幅值为0.8 A，正弦的频率为1.265 Hz，Im，Ir幅值比值为1.716。图11 实线为上位机检测到的电流波形，虚线为经傅里叶变换的电流基波幅值计算波形。图12为傅里叶变换电流基波相位计算波形，由图可知傅里叶变换在一个正弦周期后达到稳态。图13为互感辨识的电流实际波形图。

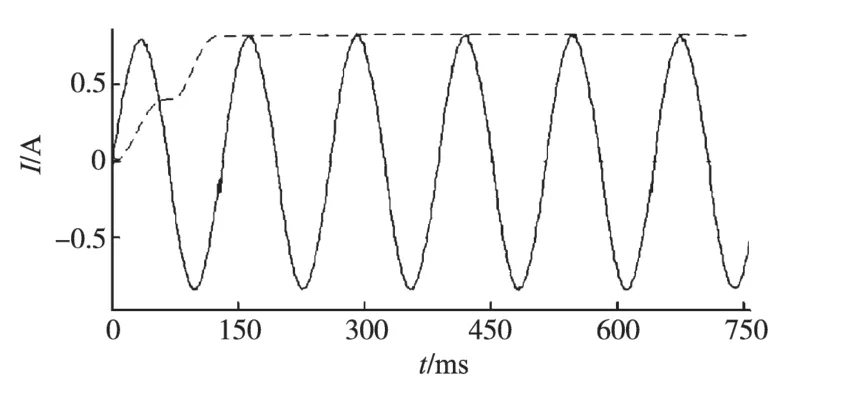
图11 采样电流及其基波幅值Fig.11 Sampling current and its fundamental amplitude

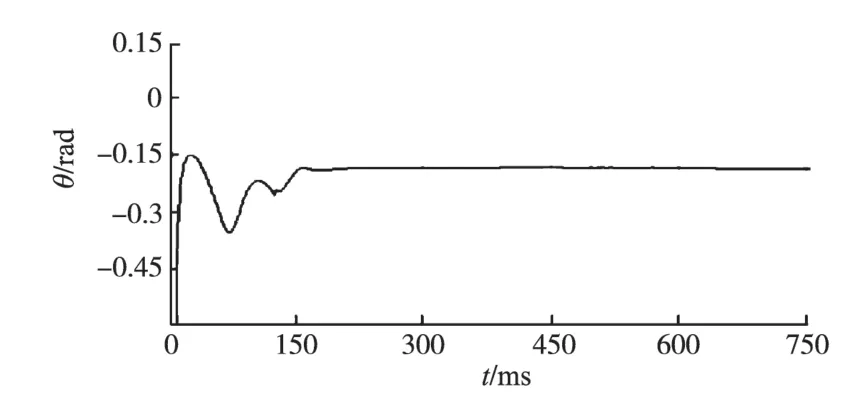
图12 采样电流基波相角Fig.12 Fundamental phase angle of sampling current

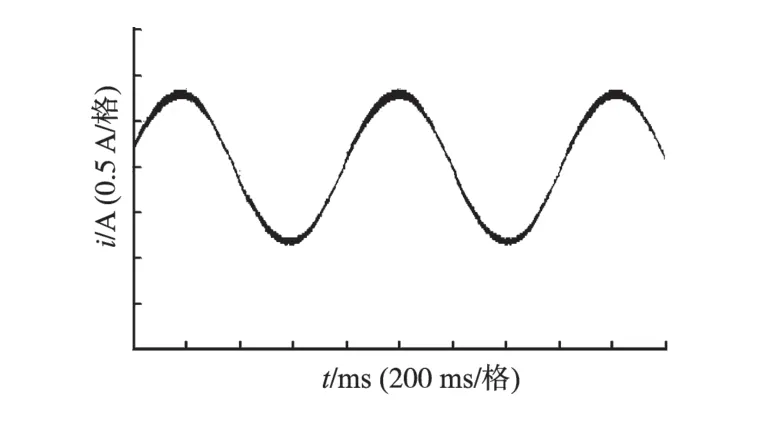
图13 单相正弦电流实测波形图Fig.13 Actual measured value of singlephase sinusoidal current

比较图11、图13，可以看出检测电流与实际电流相差不大。实验得到10组结果，然后取平均值，得最终辨识结果。表2 为互感辨识结果。

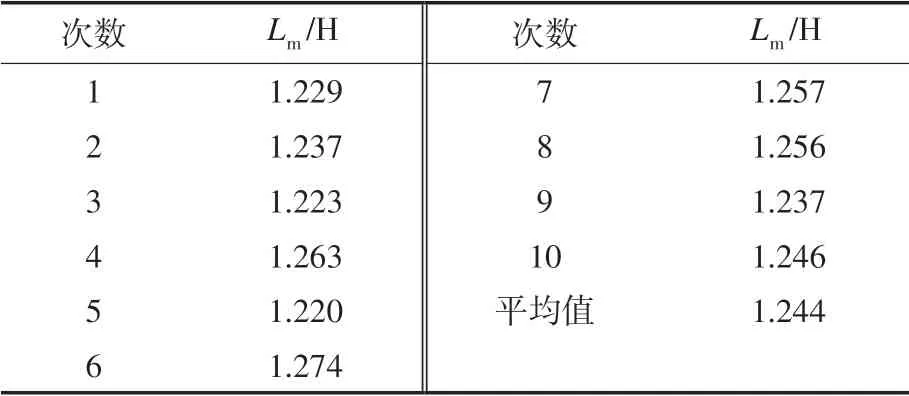
表2 互感辨识结果Tab.2 Identification results of mutual inductance

6 结论

本文在异步电机反Г型等效电路的基础上提出了一种辨识定转子总漏感与互感的方法，并对激励信号的产生以及数据采样和处理的方法做了简单描述。从实验结果来看，辨识得到的漏感及互感与传统手动试验的结果较为接近，且辨识结果具有较强的重复性，可以保证辨识的精度。辨识过程中的每个实验都由系统自动完成，辨识方法简单易行，无需人工连线，无需机械堵转，应用方便。

［1］陈伯时.电力拖动自动控制系统［M］.北京：机械工业出版社，2008.

［2］李发海，王岩.电机拖动基础［M］.北京：清华大学出版社，2005.

［3］姚立海，姚立敏，黄进．基于DAQ 的电机测试系统［J］.电机电器技术，2002（3）：47-49.

［4］韩泰安，刘峙飞，黄海.DSP 控制原理及其在运动控制系统中的应用［M］.北京：清华大学出版社，2003.

［5］Gastli A，Matsui N.Stator Flux Controlled V/f PWM Inverter with Identification of IM Parameter［J］.Industrial Electronics，IEEE Transactions，1992（34）：334-340.

［6］李正熙，杨立永.交直流调速系统［M］.北京：电子工业出版社，2013.

［7］陈伟，于泳，徐殿国，等.基于自适应补偿的异步电机静止参数辨识方法［J］.中国电机工程学报，2012，32（6）：156-162.

［8］Song Seung-Ho，Choi Jong-Woo，Su1 Seung-Ki.Current Measurements in Digitally Controlled AC Drives［J］.IEEE Industry Application Magazine，2000，6（4）：51-62.

［9］吴静，金海彬.高精确度的相位差测量方法［J］.中国电机工程学报，2010，30（13）：41-45.