ANSYS/PDS在连杆可靠性设计中的应用
2015-07-11孙志娟戴京涛
孙志娟,戴京涛
(1.国家开放大学 理工教学部,北京 100039;2.海军航空工程学院青岛校区 航空机械系,青岛 266041)
0 引言
采用有限元方法在进行结构设计时,将结构尺寸、载荷、材料性能参数等均视为固定值,所得设计结果也是确定的。设计结果通过安全系数来保证结构的安全性,但安全系数法无法反映出结构的安全程度[1,2]。机械可靠性设计方法考虑了结构各设计参数的分散性,结合概率与数理统计理论及强度理论,从而得到结构的安全性评价结果。
连杆是活塞压缩机中运动和动力传递的重要零件,它在运转过程中承受周期性变化的拉力、压力及惯性力等外载荷,受力状态较复杂,是主要受力构件之一[3~5]。统计资料显示,在活塞压缩机故障中,连杆故障是最常见现象之一。因此,连杆结构的高可靠性是压缩机正常工作的重要保证。文中采用确定性有限元方法和可靠性设计方法对连杆在工作载荷下的可靠性进行分析,分析结果对连杆结构的进一步优化设计提供理论依据。
1 可靠性设计的基本原理
在机械结构可靠性设计中,主要任务就是探究应力与零件强度的分布规律,建立应力与强度之间的数学模型[6],控制失效概率,以满足设计要求。控制结构材料的强度极限值大于结构的工作应力值以确保结构的安全性,当应力小于强度时,结构处于安全状态,否则认为结构失效。失效准则可表示为:

式中,σmax为零部件最大应力值;
σs为零件材料强度极限。
考虑零部件的结构尺寸、载荷等因素的不确定性,考查结构的应力和强度之间的关系,将结构的极限状态通过功能函数(或极限状态函数)Z(X)来定义:
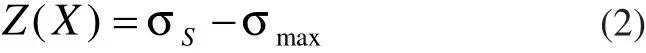
其中X为随机输入变量向量,当Z(X)<0时,结构为失效状态,Z(X)<0的概率即为结构的不可靠度;当Z(X)=0时,结构处于临界状态;当Z(X)>0时,结构安全,Z(X)>0的概率即为结构的可靠度。
2 基本方法
蒙特卡罗法是一种用数值模拟来解决复杂结构可靠性的方法之一[7]。蒙特卡罗法又称为统计试验法,该方法依据统计抽样理论,利用计算机研究随机变量的数值计算方法。用蒙特卡罗法表示结构的失效概率如下:

式中,Pf为结构失效概率;
N为抽样模拟次数;
Z(Xi)为功能函数;
Xi为随机变量抽样值。
蒙特卡罗法适用面广,分析精度与抽样次数有密切的关系。当抽样次数足够多时,在系统模型准确的前提下,分析结果就可认为是可信的。蒙特卡罗模拟是目前可靠度分析结果正确性验证的唯一手段。
3 活塞压缩机连杆的有限元分析
3.1 连杆工作载荷分析
连杆在工作过程中,作用于其上的力主要有活塞组的往复惯性气体压力、活塞组的往复惯性力和连杆的惯性力[8,9]。气体压力作用于活塞上,气体压力大小随活塞运动周期性变化;活塞组的往复惯性力由活塞组的往复直线运动引起;连杆的运动是随活塞往复运动和绕活塞销摆动的复合运动,这两种运动都是变速运动,由此产生连杆的惯性力。
建立曲轴连杆系统的动力学仿真模型,施加气体作用力和相关约束,忽略两端的曲柄销孔和活塞销孔所受的摩擦力,得到连杆的受力情况如图1所示。
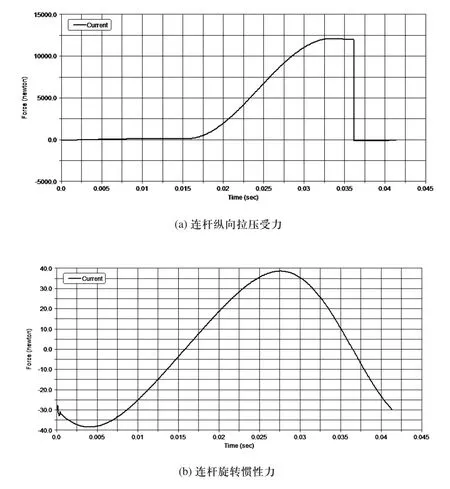
图1 连杆受力图
由图1可知,连杆旋转惯性力值远小于连杆纵向拉压受力值。因此,在连杆可靠性分析中,重点研究纵向拉压载荷对连杆可靠性的影响。
3.2 连杆参数化有限元模型的建立
APDL是有限元软件ANSYS提供的是一种解释性语言[10],其命令流不受软件版本和系统平台的限制,适用于复杂模型以及需要多次重复分析模型的建立,从而可以有效地提高分析速度和设计效率。
连杆的实际结构比较复杂,利用参数化建模思想,根据连杆的几何结构抽象出描述连杆模型的特征参数,并对结构中的一些微小结构(如小圆角、小倒角等)在不影响分析精度的情况下做适当简化。并利用APDL语言将抽象出的特征参数代替连杆建模过程中的结构参数,构成可变参数的连杆结构模型。连杆结构尺寸参数如表1所示。

表1 连杆结构尺寸参数 (单位:m)
采用参数化建模方法完成的连杆结构如图2所示。

图2 连杆三维模型
设置连杆材料常数E=70×109Pa,泊松比为0.3。采用20节点等参单元对连杆进行网格划分,连杆有限元模型如图3所示。
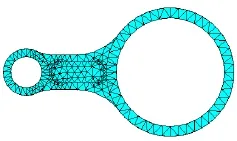
图3 连杆有限元模型
3.3 连杆应力求解
在对连杆进行强度分析时,为降低计算的难度,一般会简化其受力情况,将最大工作载荷以静载荷的方式集中施加。但这种计算方法的结果不够精确,会使后续的连杆可靠度计算产生误差。文中模拟连杆的受力状态时,参考现有较成功的处理方法,将连杆最大工作载荷以分布载荷的形式进行分析,将载荷作用在小头孔内表面上下120°范围内,沿轴线方向按二次抛物线分布,沿圆周方向呈余弦分布。在连杆大头约束连杆的刚性位移,得到连杆在最大工作载荷作用下的应力分布如图4所示。
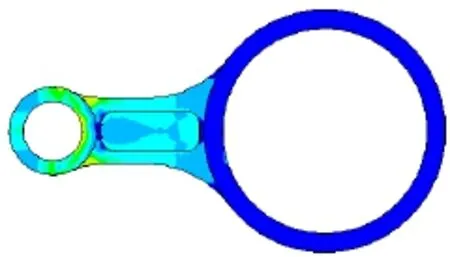
图4 连杆应力云图
如图4所示,在连杆小头内表面应力值最大,最大应力值为116MPa,小于连杆材料抗拉强度值204MPa,连杆静强度满足要求。
4 活塞压缩机连杆的可靠性分析
连杆的工作载荷、结构尺寸等参数的分散性对连杆的应力分布产生影响,进而影响连杆结构的可靠度。定义各随机输入变量分布情况如表2所示。
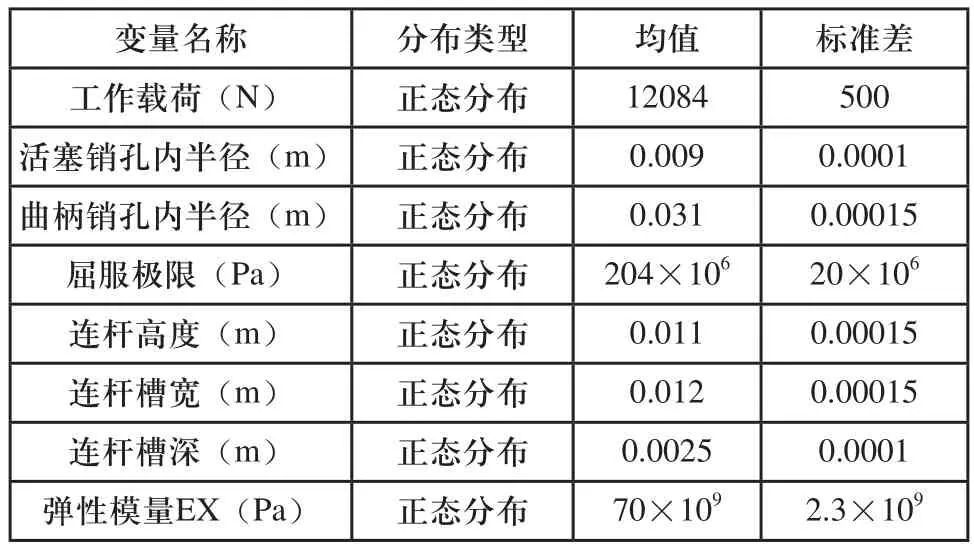
表2 随机变量及分布
根据连杆应力分析结果,提取节点最大应力值,定义极限状态方程,并生成概率分析文件。进入ANSYS软件概率设计模块,定义各输入输出变量,选择蒙特卡罗方法来进行连杆可靠性分析,设置模拟样本数为400,得到图5所示的输出变量均值趋势图。检查蒙特卡洛法循环次数是否足够的最有效方法是查看输出变量均值的历史,当模拟次数足够多的时候,输出变量的均值是逐渐收敛的,曲线趋向水平。从图5中可看出输出变量均值曲线趋向相对平稳,说明样本数目已经足够。

图5 Z抽样过程显示
输出变量在置信度95%下的累积分布函数如图6所示。由图中可知,在Z(X)<0,置信度为95%时的概率为0.403%,即连杆可靠度为99.597%。因此,连杆设计结果已经能够满足结构安全性要求。
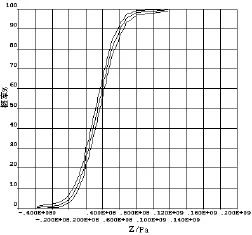
图6 Z在置信度95%下的累积函数分布图
5 结论
1)文中提出了活塞压缩机连杆的可靠性设计方法,对连杆结构采用参数化建模,同时考虑了有关设计变量离散性的影响,使得设计结果更具有工程应用价值。
2)采用ANSYS/PDS方法进行连杆结构可靠性设计,避免了大量的试验,缩短了产品开发周期。上述方法可为相关复杂结构可靠性分析提供参考,并为连杆结构的进一步优化提供指导。
[1] 莫文辉.机械可靠性设计与与随机有限元[M].昆明:云南科技出版社,2010.
[2] 赵知辛,王方成,荆浩旗.基于有限元的发动机连杆可靠性分析[J].组合机床与自动化加工技术,2014(9):35-38.
[3] 戎志祥,林少芬.基于随机有限元法的连杆可靠性分析[J].舰船科学技术,2011(9):68-70.
[4] 黄天成,张炎,王宏丽,等.基于ANSYS/PDS的抽油机支架可靠性分析[J].制造业自动化,2011,33(7):119-121.
[5] 林国庆,王茂廷,林猛.汽车发动机连杆在拉压工况下的可靠性分析[J].辽宁石油化工大学学报,2011(3):50-53.
[6] 刘惟信.机械可靠性设计[M].北京:清华大学出版社,1996.
[7] 余伟炜,高炳军.ANSYS在机械与化工装备中的应用[M].北京:中国水利水电出版社,2007:341-346.
[8] 庹奎,胡启国,谢国宾.基于ANSYS的连杆结构强度混合可靠性分析[J].组合机床与自动化加工技术,2014(6):113-117.
[9] 李太福,王栓虎,秦为前,等.基于ANSYS的高速冲床连杆疲劳可靠性分析[J].机床与液压,2014(6):189-192.
[10] 李浩月,周田朋,刘相新.ANSYS工程计算应用教程[M].北京:中国铁道出版社,2003.
