高速主轴系统热特性分析与实验

马 驰，杨 军，赵 亮，梅雪松，施 虎，王新孟

（西安交通大学 机械制造系统工程国家重点实验室，陕西 西安710049）

高速与高精度加工是现代制造业的发展方向，而高速主轴的应用对实现高速与高精度加工至关重要.但是，为了改善传动性能，高速主轴引入内置电机与高速轴承，导致主轴受内部与外部多种热源的影响，加之主轴部件材料性能各异，且结构复杂，导致热源位置、强度、膨胀系数及主轴结构的相互耦合产生了复杂的热特性，导致主轴温度场分布不均匀引起了热误差，并具有时变非线性非稳态特性；大量研究表明，热误差是导致机床精度降低的主要因素之一，其中热误差约占机床总误差的70%［1-2］，且机床越精密，热误差占机床总误差的比重越大，可见，热误差是引起数控机床精度降低的主要误差源.因此，研究高速主轴系统热特性能够有效避免实际加工中由于温度场分布不均导致机床加工精度降低的问题.

提高机床加工精度是学者们的毕生追求，热误差建模与补偿对提高机床加工精度至关重要，通过模糊聚类分析，杨建国等［3］应用回归分析方法建立了主轴热变形与温度场间的线性函数映射关系，YANG 等［4］利用神经网络建立主轴热误差与温度间的非线性函数映射关系.杨军等［5］利用时间序列模型的预测精度高、计算速度快等特点建立了热误差建模.进给系统热特性研究也是提高机床加工精度的一个研究方向，杨军等［6］利用激光干涉仪，红外热像仪及温度位移测量系统，研究了不同进给速度下的机床热特性.近年来，利用有限差分（FDM）与有限元（FEM）理论分析机床温度场分布规律及热变形变化的方法成为研究热点，Bossmann等［7］使用有限差分法研究了主轴系统生热机理与散热机制，Zhao等［8］建立了主轴热特性分析模型，并研究了主轴温度场分布及热变形变化规律，Creighton等

［9］及Kyung等［10］研究了主轴-轴承系统在高速运转时的动态与热态特性，Holkup等［11］与Kolar等

［12］建立了预测主轴温度场分布、热伸长、轴承刚度、动态特性与接触载荷的热力学模型.上述模型都将热载荷与对流换热系数等作为重要的边界条件，但没有意识到结合面与连续体传热间的区别，因此，忽略了接触热导对温度场与热变形等仿真结果的影响，有些学者将各种不同结合面间接触热导设置为经验常数，导致热特性仿真精度较低.事实上，结合面间接触热导与接触材料的表面粗糙形貌、接触压力、微凸体变形形式、材料属性及温度等因素是非线性函数关系，因此，在进行热特性仿真时，忽略结合面间接触热导或将设置为经验常数是不合理的.另一方面，主轴系统中有大量的结合面，如轴承与轴、轴承与轴承座、主轴箱与端盖等，当两粗糙表面接触时，由于表面粗糙度的存在产生了非完美接触，即使结合面间压力很大，两粗糙表面的非完美接触也会使得热量传递在结合面处受阻，而产生明显的温度降，尤其是靠近热源处的接触热导对主轴热特性仿真结果影响很大.

本文以高速主轴为研究对象，建立了三维有限元模型进行高速主轴的瞬态热-结构耦合分析.建立基于几何-力学-热分析的综合接触热导预测模型以考虑结合面间接触热导对主轴温度场与热变形仿真结果的影响，基于分形理论建立了通用的接触热导预测模型，考虑了粗糙表面形貌与微凸体3种接触变形对接触热导的影响，有效避免了基于传统统计学理论与实验测量法的精度不足及通用性弱等缺点；运用拟静力学分析方法求解角接触球轴承生热功率；应用数值传热学基本理论求解主轴部件的对流换热系数，将上述边界条件施加到主轴热-结构分析模型中以提高仿真结果的精度，并进行热特性实验验证该有限元模型的正确性，为高速主轴热平衡设计提供有益帮助.

1 主轴系统

本文的建模对象为高速电主轴，实体模型如图1所示.主轴最高转速nmax＝30 000r／min，主轴两端安装有一对型号为FAG B7205-C-T-P4S的角接触球轴承，其安装方式为背对背，使用预紧螺母对轴承进行压紧，预紧力为600N，主轴冷却系统的工作机理为通过感应出水口温度控制系统温度变化，当出水口温度高于零界温度时，冷却系统开始工作，2个配重盘安装在主轴两端以调节主轴回转误差，4个温度传感器安装在主轴系统内部以测量前轴承、后轴承、电机定子与冷却水套的温度.

图1 高速主轴实体模型Fig.1 Solid model of high-speed spindle

2 主轴热特性分析模型

为了得到温度场与热变形的准确数值解，应对实体模型进行合理简化，且对实体模型进行恰当的网格划分，仿真结果的可信度依赖于边界条件如接触热导、热载荷及对流换热系数等设置是否合理.对该有限元模型做如下假设：1）忽略主轴系统与环境间的相互热辐射；2）假设冷却水套内流体流速足够大，且恒定，流体的速度波动可以忽略；3）假设环境温度恒定为15 ℃.

2.1 有限元模型

对螺栓孔、键槽与内外倒角等对主轴温度场与热变形仿真结果影响很小的结构进行合理简化，考虑到轴承转速很高，可将轴承简化为一空心圆柱体.使用具有20节点的正六面体网格对实体模型进行剖分，为了保证仿真结果的可信度，并保证在整个热平衡过程中主轴温度场分布和热变形的变化与主轴转速严格同步，对温度梯度较大的区域网格划分较细，如轴承与电机处，该有限元模型共有298 147个实体单元与1165 521个节点，如图2所示.

在没有热量传递或者热量传递不明显的位置，接触热导对结合面间热量传递的阻碍作用并不明显，而靠近热源处的接触热导对结合面间传热影响很大，如轴承内圈与轴，轴承外圈与轴承座处的接触热导，这些位置处的接触热导直接影响由轴承传递进入轴与轴承座热量的多少，而由轴承传递进入轴与轴承座的热量对主轴的温度场分布与热变形变化影响很大，在高速主轴系统中，轴承是主要热源，由于轴承内圈与轴，轴承外圈与轴承座处的接触热导靠近热源，其余位置如主轴箱与端盖处的接触热导远离热源，因此，除轴承处的接触热导外，其余位置处的接触热导对主轴系统的热特性的影响可以忽略.主轴系统部件的材料如表1 所示.表中，ρ 与c分别表示主轴部件材料的密度与比热容，E 为弹性模量，ν 为泊松比，α 为热伸长系数，λ 为热导率.瞬态热分析的控制方程可表示为

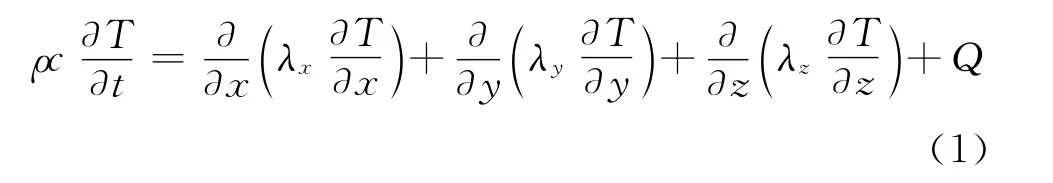
式中：T 为热力学温度，T ＝T（x，y，z，t）为随时间与位置分布的温度场，λx、λy与λz分别表示x，y 与z方向的热导率，Q 为内部热源.

图2 有限元模型Fig.2 Finite element model

表1 主轴系统材料Tab.1 Materials of spindle system

基于胡克定律计算热变形，如方程（2）所示

式中：ε为应变，ΔT 为温升.

2.2 接触热导模型

由于没有意识到连续体与结合面间传热的区别，因此，传统主轴热特性分析模型［7-12］都忽略了接触热导对温度场与热变形仿真结果的影响，一些学者将接触热导设置为经验常数，导致了温度场与热变形的仿真精度较低；另一方面，从微观角度看任何表面都是粗糙的，即粗糙表面是由大量不同尺度的微凸体组成，因此，两粗糙表面间的接触发生在有限离散点上，当热流通过非完美接触表面时，热流会在这些离散点处发生收缩，即当热量从一个物体传递到另一个物体时，在结合面处受到阻碍，接触热导的存在导致了热量不能顺利通过结合面，这样在结合面两侧会产生明显的温度降.现有文献中关于接触热导的研究方法大多是基于统计学理论［13-14］与实验测量法［14-15］.然而，基于统计学理论的研究方法［13-14］对采样长度与测量仪器的分辨率很敏感，而实验直接法［14-15］也有其缺点，如通用性不强，适应性差，并且实验结果具有一定的不确定度，且当材料、表面粗糙度、加工方法与表面接触压力等任一因素改变时，就要重新设计实验；并且，结合面间接触热导的预测是一个跨学科问题，包括，即几何、力学与热3个子问题，且接触热导分析的核心是几何及力学问题，因此，在进行主轴热特性分析中，提出基于几何-力学-热分析综合的接触热导模型以考虑其对主轴热特性仿真结果的影响.

2.2.1 分形表面表征 分形几何学中的Weierstrass-Mandelbrot函数［16］（W-M）被用来表征具有无序、非静态随机与自仿射等特性的粗糙表面形貌，本文利用WM 函数对轴承内外圈粗糙形貌进行表征：

式中：x 与z（x）分别为粗糙表面的测量位置与轮廓高度函数，D 与G 分别为粗糙表面轮廓分形维数及尺度常数，常数γ 为大于1 的非整正数，n1与粗糙表面的最低截断频率有关.

Majumdar与Tien［17］给出了W-M 函数的功率谱函数：

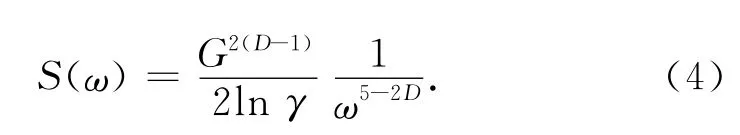
式中：w 为频率.

W-M 函数也满足如下关系

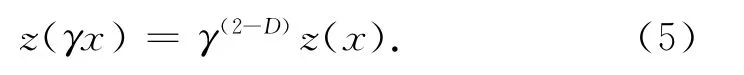
可从方程（4-5）看出W-M 函数是自相似函数，因此，其对采样长度与测量仪器的分辨率不敏感，且分形参数G 与D 是尺度独立的参数.对方程（4）两端取对数，可得

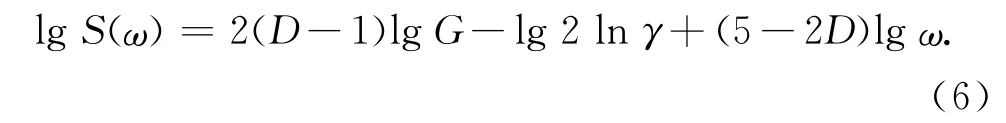
由方程（6）可看出，在双对数lg（ω）-lgS（ω）坐标系中，W-M 函数的功率谱函数近似为一条直线，该直线斜率为（5-2D），其在纵坐标轴上的截距为2（D-1）lg G-lg 2lnγ.如图3所示为D＝1.6、G＝9.46×-6m、L＝1μm 且γ ＝1.5 时，利用W-M函数仿真的三维分形粗糙表面形貌及其等高面.

2.2.2 微凸体变形特性 为了确定结合面间的接触参数，有必要对微凸体的3种变形形式：弹性、弹塑性与塑性变形进行研究.Mikic［18］提出了结合面间接触热导的预测模型，该模型假设所有微凸体均发生弹性变形，Yovanovich［19］提出了假设所有微凸体均发生塑性变形的接触热导的预测模型.事实上，在载荷的作用下，微凸体会发生弹性、塑性与弹塑性3种变形.因此，Mikic［18］与Yovanovich［19］提出的模型所做的假设并不合理.

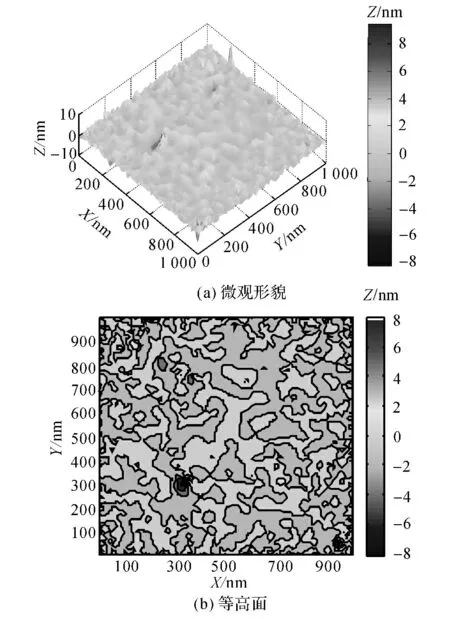
图3 三维分形表面形貌Fig.3 Three-dimensional fractal surface morphology

当微凸体所受最大赫兹接触压力达0.6 H 时，微凸体开始发生塑性变形，与微凸体发生塑性变形开始时刻对应的零界接触面积ac1［20］可表示为

式中：H 为两接触材料中较小的微观硬度，1／E ＝（1-ν）／E1＋（1-ν22）／E2，其中E1，E2，ν1，ν2分别表示两接触材料的弹性模量与泊松比.

当微凸体所受最大接触压力达到H 时，微凸体发生完全塑性变形，与微凸体发生完全塑性变形时刻对应的零界接触面积ac2可表示为

接触面积处于a 与a＋da 间的微凸体数量n（a）［17］可表示为

式中：aL为微凸体最大接触面积.

所有微凸体的总接触面积Ar可表示为

当D ≠1.5时，整个接触面上的载荷F 可表示为

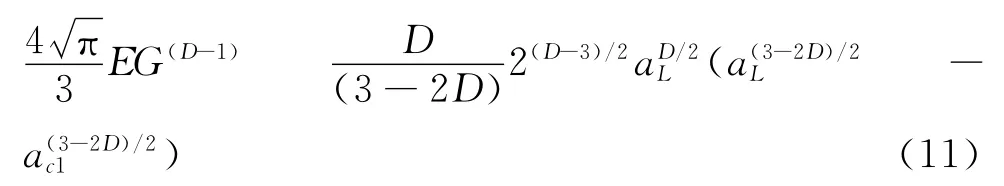
当D＝1.5时，整个接触面上的载荷F 可表示为

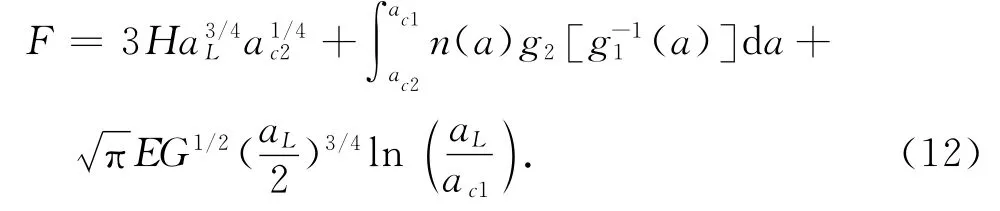
2.2.3 接触热导模型 处于接触状态的微凸体会发生3种变形形式：弹性、弹塑性与塑性变形，处于3种变形形式的单个微凸体形成的接触热导hce、hcep与hcp可分别表示为

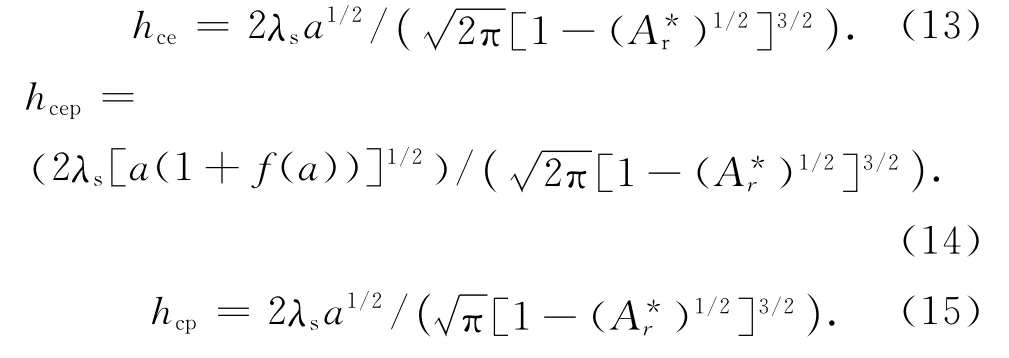
结合面间总接触热导Hc可表示为

当D ≠1.5时，结合面间总接触热导Hc可表示为

当D ＝1.5时，结合面间总接触热导Hc可表示为

［18］与Yovanovich［19］的统计学模型的预测精度高，因此，基于几何-力学-热分析的综合接触热导模型更加合理.

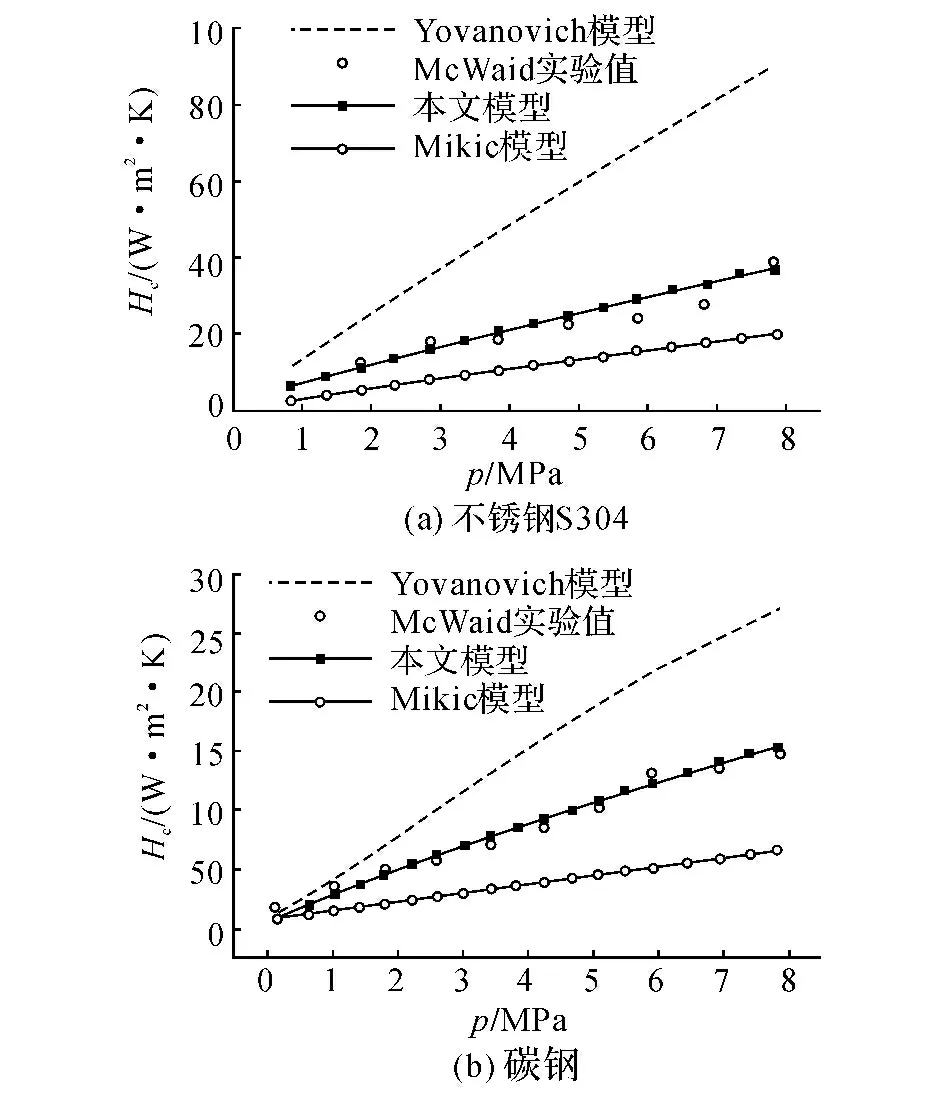
图4 接触热导预测值与现存模型及实验数据的比较Fig.4 Comparison of predictions by present model with existing models and experimental data

2.3 热源生热功率

2.3.1 电机生热功率 精确计算电机铜损、铁损及其他附加损耗非常困难，因此，本文采用效率分析法求解电机生热功率.电机风损为

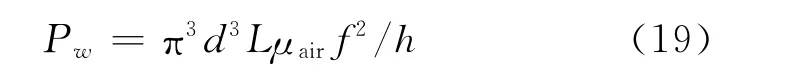
式中：d 与L 分别为转子外径及长度，h 为定转子间的间隙厚度，μair为空气的动力黏度，f 为转子转动频率.

电机效率［21］为

式中：Pbearing为轴承功率损耗，其计算方法将在2.3.2部分详细讨论，Pout为输出机械能，当主轴无负载运行时，Pout＝0，Pin为电机输入功率.

电机生热功率Pmotor可由方程（19）与（20）得到

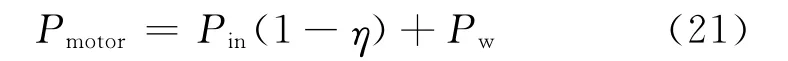
电机生热功率在定子与转子间的分配由电机转差率fslip与同步频率fsync共同决定［22］

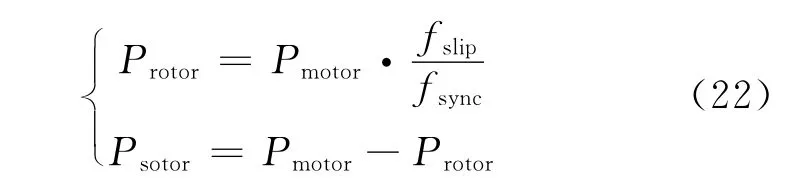
式中：Protor与Pstator分别为转子与定子生热功率.

2.3.2 轴承生热功率 Harris［23］给出了角接触球轴承生热功率P 的表达式

式中：n与M 分别表示轴承转速与其摩擦力矩.轴承摩擦力矩M 由负荷项Ml与速度项Mv组成

1）轴承外载荷引起的摩擦力矩Ml

外载荷引起的摩擦力矩Ml［23］可表示为

式中：f1为与轴承结构有关的系数，dm为轴承中径，Fβ由 轴 承 受 力 状 态 决 定，且 Fβ＝max…（0.9Fa／tanα-0.1Fr，Fr），Fa与Fr分别为轴承轴向与径向载荷，α为轴承受载后的接触角.

2）润滑剂黏性摩擦引起的摩擦力矩Mv

由润滑剂黏性摩擦引起的摩擦力矩Mv［24］可表示为

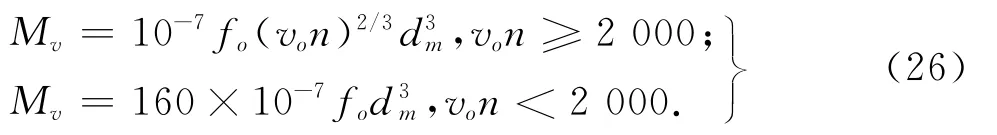
式中：vo为润滑剂的运动黏度，fo与轴承类型及润滑方式相关.

2.4 对流换热

对流换热系数αh

［25］可表示为

式中：hgap为水力半径，λf为流体导热系数，Nu 为努塞尔数.努塞尔数可根据不同的对流换热模型进行计算，如表2所示.

表2 努塞尔数的计算Tab.2 Calculation of Nusselt number

表中：Pr 为普朗特数，Re为雷诺数，lt为冷却水道长度，w 为水流平均速度，η为流体动力黏度，dk为回路直径，ds为主轴箱直径，g 为重力加速度，ξ为摩擦因数，ξ＝1／［0.79ln（Re）-1.64］2.

3 实验系统和测量原理

3.1 热特性实验

实验系统如图5所示，主轴系统最高转速nmax＝30 000r／min，冷却方式为智能温度控制，系统内部温度控制在0～70 ℃，以防止其温度过高而突然失效，最大热伸长40μm，X 与Z 方向最大径向热变形分别为50与20μm.测量设备及功能如下：温度位移测量系统是基于美国NI-SCXI1600架构的，利用精密磁吸式温度传感器PT100测量主轴系统温度，其安装位置如下：前轴承（T1），后轴承（T2），电机（T3），冷却水套（T4），环境（T5），主轴壳体（T6）.应用高精密电涡流传感器测量主轴热漂移，其安装位置如图5与6所示，且温度位移测量为同步测量.

3.2 分形参数辨识

利用OLYMPUS LEXT OLS4000型激光共聚焦显微镜对轴承部件粗糙形貌进行测量，如图7所示.

图5 热特性测试实验现场Fig.5 Thermal characteristic experiment

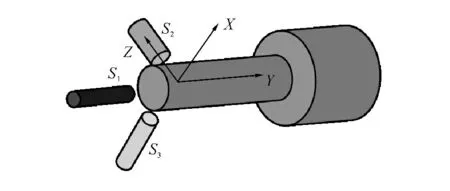
图6 位移传感器安装方式Fig.6 Spindle three-spot installation diagram

如图8所示为轴承外圈表面三维粗糙形貌，外圈表面沿X 方向轮廓高度如图9所示，其中R 表示为粗糙表面轮廓高度，其值作为分形参数的辨识数据源，S 为采样长度.

图7 OLYMPUS LEXT OLS4000型激光共聚焦显微镜Fig.7 Olympus LEXT OLS4000laser microscope

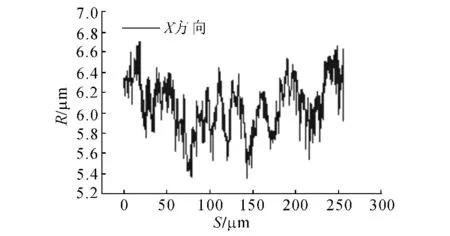
图9 轴承外圈X 方向轮廓高度Fig.9 Profile Height of Xdirection

利用如图9所示轴承外圈表面沿X 方向轮廓的数据，并结合方程（4）求得粗糙表面轮廓的功率谱函数，如图10所示，并应用最小二乘法对粗糙表面轮廓的功率谱函数进行拟合，可得外圈的分形参数为G＝1.66，D＝7.8×10-14m，同理，可计算轴承内圈表面的分形参数.

4 仿真结果及实验对比分析

4.1 温度场分析

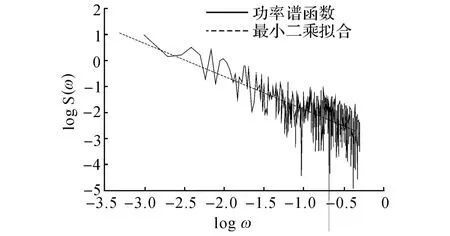
图10 轴承滚道功率谱与其最小二乘拟合曲线Fig.10 Power spectrum and least-squares fitting curves of Xdirection morphology

图11 主轴转速分布图Fig.11 Spindle speed distribution

图12 主轴系统温度场云图Fig.12 Nephogram of temperature field distribution when thermal equilibrium

为了模拟主轴实际加工状态，设计主轴转速分布如图11所示，达到热平衡状态时，主轴系统的温度场分布如图12所示.主轴系统内部温度场不均匀且梯度明显，最高温度θ＝55.37 ℃（转子），t为时间，电机定子生热功率（1 635 W）是主轴系统所有部件中最大的，但其温度却不是最高的，这是因为定子与冷却系统间对流换热明显，显著降低了定子的温度.冷却水套带走了定子大部分热量，因此，冷却水套温度升高了，但是，冷却水套与主轴箱接触，有相当一部分热量由冷却水套传递进入主轴箱，主轴箱温度也相应升高.

前轴承温度最高可达41.2℃，且前轴承较后轴承更加靠近电机转子，因此，由转子经轴进入前轴承的热量多于进入后轴承的热量，因此，前轴承温度高于后轴承.轴承与轴承座，轴承与轴间温度梯度明显，这是因为这些位置处存在接触热导使得轴承热量扩散到轴承座与轴更加困难，但是，在主轴运转过程中，轴承仍在不断产生热量，因此，由于接触热导的阻力作用使得轴承产生的热量在其自身上发生了累积，导致其局部温度过高.将前轴承、后轴承、电机定子与冷却水套温度的仿真值与实验值进行比较，如图13所示，可以看出，考虑结合面间接触热导的有限元模型能准确预测测点温度，且测点温度在初期迅速上升，然后逐渐饱和到最终温度.

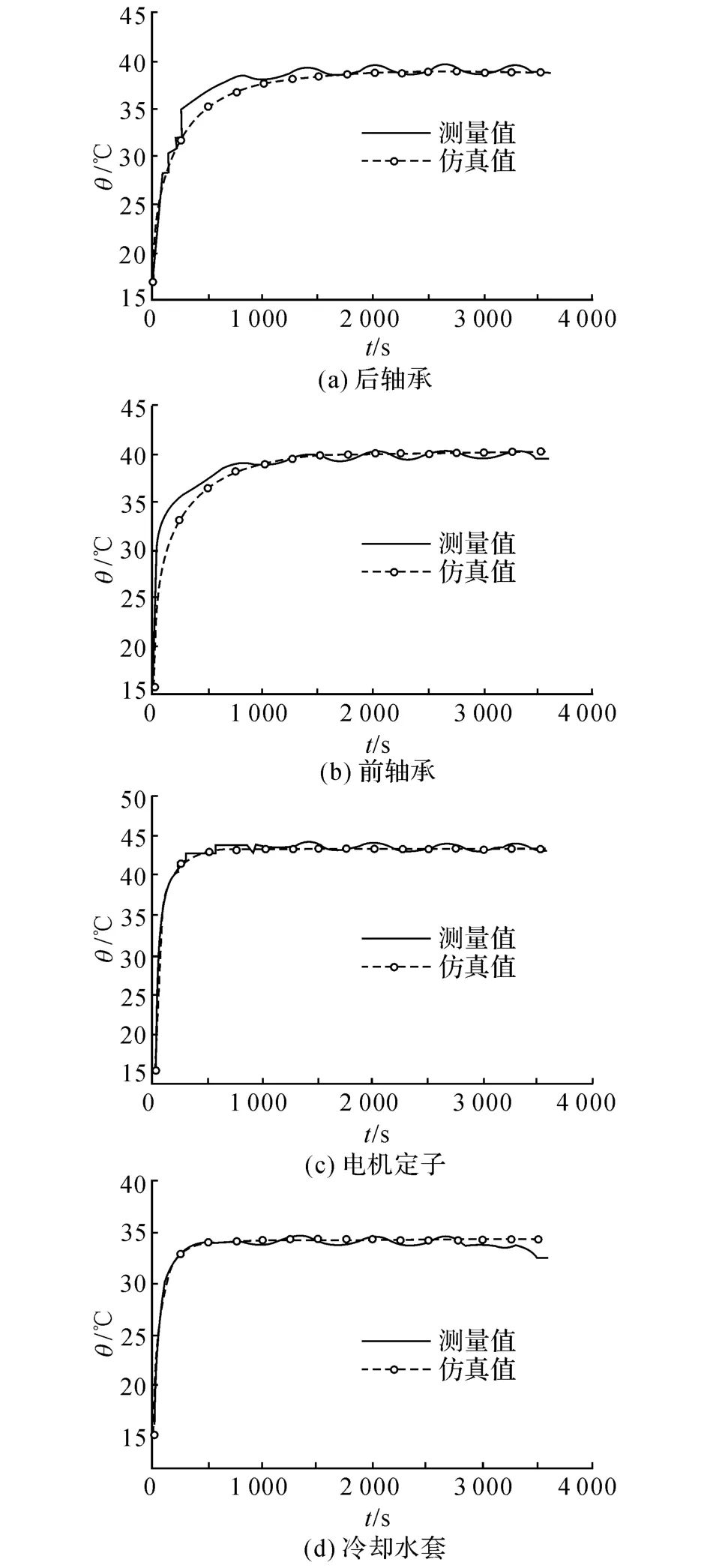
图13 温度测量值与仿真值比较Fig.13 Comparison of the temperature histories，simulated，experimental

为了验证结合面间接触热导对仿真结果的影响，对忽略接触热导的有限元模型进行仿真，并将前轴承与后轴承温度分别与测量值和考虑接触热导的有限元模型进行比较，如图14所示，可以看出，考虑接触热导的有限元模型的仿真精度远高于不考虑接触热导的有限元模型.且考虑接触热导时，前后轴承温度分别高于不考虑接触热导时的前后轴承的温度.原因如下：结合面间接触热导的存在使得由一个物体向另一个物体的传热受到阻碍，即考虑接触热导时，由于轴承内圈与轴，轴承外圈与轴承座间接触热导的存在，使得轴承（热源）产生的热量传递到轴与轴承座变得更加困难，即轴承结合面间接触热导的阻碍作用限制了热量从轴承传向轴与轴承座，但是，在主轴持续运转过程中，轴承（热源）仍然在不断的产生热量，因此，热量在轴承上产生了积累，使得轴承局部温度过高，故当考虑接触热导时，轴承温度比不考虑接触热导时的轴承温度高，如图14所示；而对于轴与轴承座，考虑接触热导时，由于接触热导对结合面间传热的阻碍作用，使得由轴承传递到轴与轴承座上的热量比不考虑接触热导时的热量少，因此，当考虑接触热导时，轴与轴承座温度比不考虑接触热导时的温度低.并且结合面间的接触热导越小，结合面两侧温差越大.

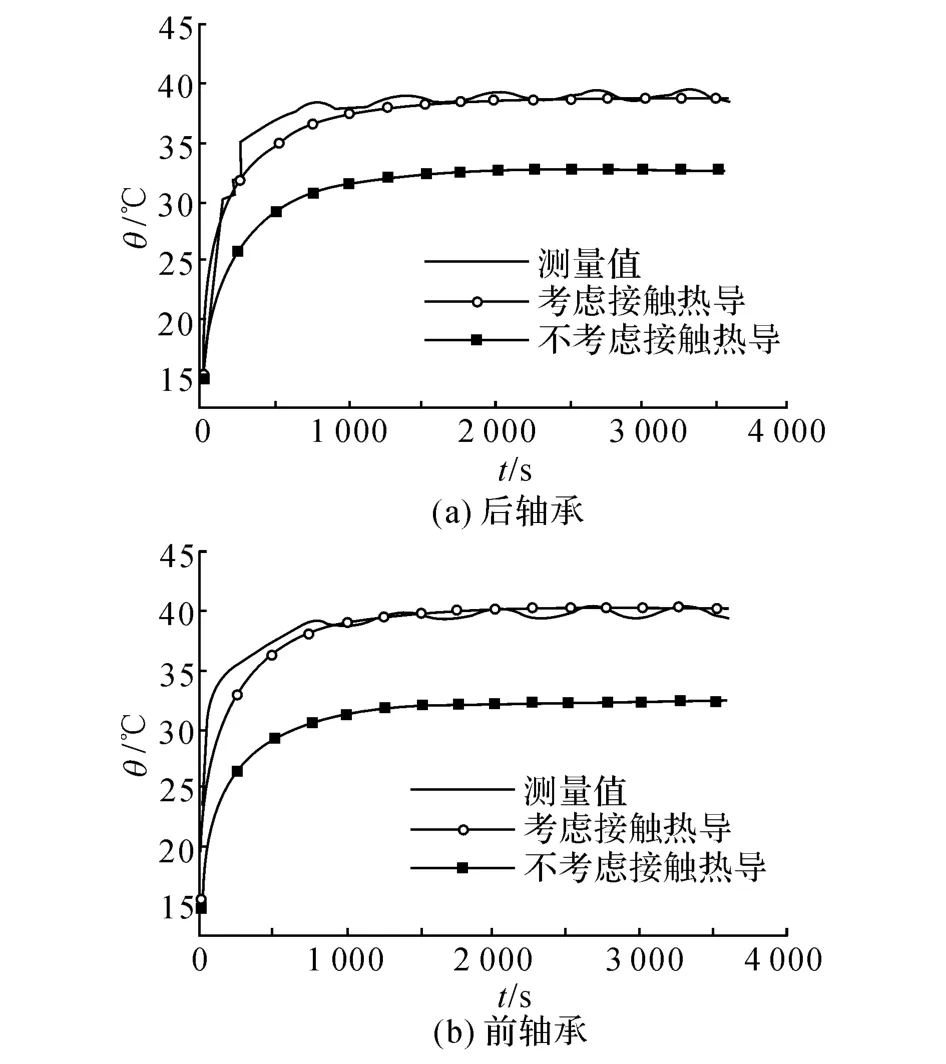
图14 温度测量值与仿真值比较Fig.14 Comparison of temperature experimental data with the simulation results

4.2 热变形分析

如图15所示为主轴系统热平衡时的热变形云图（放大250倍），可以看出，主轴系统最大变形量为60.8μm（Y＋端），主轴X、Y 与Z 方向的最大变形量分别为58.0、10.5与8.0μm，前轴承温度高于后轴承导致主轴左侧热变形较主轴右侧对应位置的热变形大.

图15 主轴系统热变形场云图Fig.15 Nephogram of thermal deformation of spindle system

为了研究主轴系统热变形对加工精度的影响，对3个方向的热变形仿真值与测量值进行比较，如图16所示，可以看出X 方向热变形最明显，其对加工精度有明显影响，Y 方向热变形也较大，即主轴会沿轴向伸长，对加工精度也有很大影响.

热变形测量值、考虑结合面间接触热导与不考虑结合面间接触热导的有限元模型的热变形的比较如图17所示，可看出，考虑结合面间接触热导的热变形的精度比不考虑结合面间接触热导的热变形精度较高，并且考虑结合面接触热导的有限元模型X，Y 与Z3个方向热变形均大于不考虑接触热导3个方向对应的热变形.原因如下：当考虑接触热导时，由轴承传递到轴的热量比不考虑接触热导时的热量少，因此，对于轴而言，其热变形也会相应减小，如图17所示.

图16 主轴X，Y 与Z 方向热变形测量值与仿真值比较Fig.16 Comparison between thermal errors of measurement data with simulation results of X，Yand Z directions

图17 主轴热变形测量值与仿真值比较Fig.17 Comparison of thermal deformations of measurement data with the simulation results with and without TCC

因此，在考虑接触热导情况下，轴承产生的热量在其自身产生了积累，且由轴承进入主轴与轴承座的热量少于不考虑接触热导时的热量，因此，考虑接触热导情况下轴承温升的仿真值大于考虑接触热导的情况，不考虑接触热导情况下其热变形值大于考虑接触热导的情况.

5 结 语

本文提出了高速主轴热特性分析的系统化建模方法.建立了基于几何-力学-热的综合接触热导预测模型，该模型考虑到粗糙表面形貌与微凸体接触变形对结合面间接触热导的影响，且有效避免了统计学方法的不准确性与实验测量法通用性不强的缺陷，分析了电机与轴承生热功率求解方法，给出了主轴部件与流体间的对流换热系数的计算方法，进行热平衡实验验证建模方法的有效性，分析了主轴温度分布规律与热变形变化，结果表明，本文建立的主轴热特性分析模型能够准确预测主轴温度场与热变形，且仿真精度远高于忽略接触热导的有限元模型.虽然本文模型是针对高速主轴建立的，但模型不失一般性，其分析方法可为机床整机或进给系统热特性仿真提供参考.结合面间接触热导模型适用于所有固定结合面间传热分析.

（

）：

［1］MAYR J，JEDRZEJEWSKI J，UHLMANN E，et al.Thermal issues in machine tools［J］.CIRP Annals-Manufacturing Technology，2012，61（2）：771-791.

［2］ABELE E，ALTINTAS Y，BRECHER C.Machine tool spindle units［J］.CIRP Annals-Manufacturing Technology，2010，59（2）：781-802.

［3］杨军，梅雪松，赵亮，等.基于模糊聚类测点优化与向量机的坐标镗床热误差建模［J］.上海交通大学学报，2014，8：1175-1182.YANG Jun，MEI Xue-song，ZHAO Liang，et al.Thermal error modeling of jig-borer based on fuzzy clustering and support vector machine［J］.Journal of Shanghai Jiaotong University，2014，8：1175-182.

［4］YANG J，SHI H，FENG B，et al.Applying neural network based on fuzzy cluster pre-processing to thermal error modeling for coordinate boring machine［J］.Procedia CIRP，2014，17：698-703.

［5］杨军，梅雪松，冯斌，等.时序分析在电主轴热误差建模中的应用［J］.计算机集成制造系统，2014（1）：10-18.YANG Jun，MEI Xue-song，FENG Bin，et al.Application of time series in the thermal error modeling of highspeed spindle system［J］.Computer integrated manufac-turing system，2014（1）：10-18.

［6］杨军，施虎，梅雪松，等.双驱伺服进给系统热误差的试验测量与预测模型构建［J］.西安交通大学学报，2013，47（11）：53-59.YANG Jun，SHI Hu，MEI Xue-song，et al.Prediction model construction and experimental measurement of the thermal error of dual servo feed drive system［J］.Journal of Xi'an Jiaotong University，2013，47（11）：53-59.

［7］BOSSMANNS B，TU J F A thermal model for high speed motorized spindles［J］.International Journal of Machine Tools and Manufacture，1999，39（9）：1345-1366.

［8］ZHAO H，YANG J，Shen J.Simulation of thermal behavior of a CNC machine tool spindle［J］.International Journal of Machine Tools and Manufacture，2007，47（6）：1003-1010.

［9］CREIGHTON E，HONEGGER A，TULSIAN A，et al.Analysis of thermal errors in a high-speed micromilling spindle［J］.International Journal of Machine Tools and Manufacture，2010，50（4）：386-393.

［10］KYUNG CHOI J，GIL LEE D.Thermal characteristics of the spindle bearing system with a gear located on the bearing span［J］.International Journal of Machine Tools and Manufacture，1998，38（9）：1017-1030.

［11］HOLKUP T，CAO H，KOLÁR P，et al.Thermo-mechanical model of spindles［J］.CIRP Annals-Manufacturing Technology，2010，59（1）：365-368.

［12］KOLAR P，HOLKUP T.Prediction of machine tool spindle's dynamics based on a thermo-mechanical model［J］.MM Science Journal，2010：166-171.

［13］GREENWOOD J A，WILLIAMSON J B P.Contact of nominally flat surfaces［J］.Proceedings of the Royal Society of London.Series A.Mathematical and Physical Sciences，1966，295（1442）：300-319.

［14］COOPER M G，MIKIC B B，YOVANOVICH M M.Thermal contact conductance［J］.International Journal of heat and mass transfer，1969，12（3）：279-300.

［15］MCWAID T H，MARSCHALL E.A comparison of elastic and plastic contact models for the prediction of thermal contact conductance ［J］. Wärme-und Stoffübertragung，1993，28（8）：441-448.

［16］BERRY M V，LEWIS Z V.On the Weierstrass-Mandelbrot fractal function［J］.Proceedings of the Royal Society of London.A.Mathematical and Physical Sciences，1980，370（1743）：459-484.

［17］MAJUMDAR A，TIEN C L.Fractal network model for contact conductance［J］.Journal of Heat Transfer，1991，113（3）：516-525.

［18］MIKIC B B.Thermal contact conductance；theoretical considerations［J］.International Journal of Heat and Mass Transfer，1974，17（2）：205-214.

［19］YOVANOVICH M M.Thermal contact correlations［J］.AIAA Paper，1982，81：83-95.

［20］MAJUMDAR A，BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces［J］.Journal of Tribology，1991，113（1）：1-11.

［21］KYLANDER G.Thermal modelling of small cage induction motors［M］.Goteborg：Chalmers University of Technology，1995：1-113.

［22］AVALLONE E A，BAUMEISTER T，SADEGH A.Marks'Standard Handbook For Mechanical Engineers：Standard Handbook for Mechanical Engineers ［M］.New York：Mcgraw-Hill Professional，2006：1-386.

［23］HARRIS T A.Rolling bearing analysis［M］.New York：Wiley，1984：1-1013.

［24］JONES A B.A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions［J］.Journal of Fluids Engineering，1960，82（2）：309-320.

［25］XU M，JIANG S，CAI Y.An improved thermal model for machine tool bearings［J］.International Journal of Machine Tools and Manufacture，2007，47（1）：53-62.