一种基于图结构分解的图近似查询方法研究*

杨书新,谭 伟,魏朝奇

(江西理工大学信息工程学院，江西 赣州 341000)

1 引言

图作为一种通用的数据结构，能够表示复杂的数据类型。近些年已经在诸多领域得到了广泛的应用，包括生物领域(蛋白质基因交互网络)、化学领域(化合物)、社会网络社区、交通网络等许多数据都利用图来进行建模。通过研究者的努力与研究，在图数据管理及分析方面，已经在一些基本问题上取得了一定的成果。例如，关于图数据库中频繁模式挖掘算法的研究在近五年时间内已经出现至少10种新的算法。而今，越来越多的学者开始关注于图数据的查询领域。图数据查询大体分为两类：精确查询和近似查询。

在图数据查询领域虽有不少研究，但是大部分的研究工作都集中在图的精确匹配查询，其算法有子图查询和超图查询两大类。子图查询中Shasha D和Wang J T L在2002 年首先提出了基于路径查询的GraphGrep算法[1]，2004年在基于路径查询的基础上Yan X等人[2]提出了利用频繁子图挖掘建立索引的gindex思想。Zou L等人[3]在2008年提出了基于树结构建立索引的 GCoding算法，其他算法还有GDIndex[4]、GString[5]等。超图查询中Chen等人在2007年提出cIndex[6]算法，利用contrast index得到不被q包含的索引模式。2009年Zhang S等人则从另一个角度出发，根据特征子图的最优排序提出了GPTree[7]算法，降低了查询的时间复杂度。

精确匹配查询虽然能够准确地找出目标图，但是由于真实数据库的数据结构复杂，图数据库具有信息不完整、含噪音等情形，精确查询过程存在节点(边)不匹配、节点错位、查询条件苛刻等问题，往往无法得到我们实际想要的结果。然而，近似查询有很好的容错性，对于节点的不匹配甚至图结构差异较大的情况，都能够得到与查询图相近似的结果集。因此，近年来近似查询开始越来越多地受到研究者们的关注。近似查询可分为k-NN查询和范围查询。k-NN查询返回与查询图q最相似的k个结果，而范围查询则返回用户定义的某个范围内的全部结果。目前研究者们对近似查询的研究主要集中在以下三个问题：(1)如何有效存储图数据；(2)如何定义图之间的相似度；(3)如何创建高效索引加速图的匹配和查询。

本文从索引构建的角度出发，提出一种基于图结构分解的索引方法，对DAG图(Directed Acyclic Graph)[8]建立索引，由查询图q的最小生成树集进行满足条件θ的生成树扩展，通过索引得到近似结果集，减少近似查询过程的子图同构验证次数，降低计算的复杂度，提高近似查询的效率。

2 图分解近似查询算法

本文中的图G可以采用一个五元组[8,9]来表示，G=(V,E,∑V,∑E,L)，其中V代表图中节点的集合，E=V×V代表图中边的集合，∑V代表图中所有节点标号的集合，∑E代表图中所有边标号的集合，L是标号与节点或标号与边之间映射关系的函数，实现标号向边和节点的映射，即L：V→∑V,E→∑E。

在图数据库GD中，给定查询图q，图近似查询可以得到所有的满足图编辑距离[4]在θ内的与q同构的图gi。存在特例θ=0，近似查询问题也即是精确查询。文献[10]中提出了一种基于闭图的图近似匹配方法C-Tree，其定义了基于编辑距离的图近似度，并且采用了启发式图匹配方法，提出了邻接子树和邻接子图方法在近似查询中的应用。但是，该算法仅仅能查询到k个最近的近似结果。对于当前信息数据的复杂化，其查询结果及效率并不理想。因此，本文提出一种基于图分解的近似查询算法，提高查询效率以及查询结果集的完整性。本文算法通过对查询图q和图数据G作DAG分解，利用分解后得到的DAG图的哈希编码构建索引，通过q的最小生成树集，枚举生成满足条件θ的生成树，将其与DAG图进行快速验证，降低同构测试次数，得到近似结果集，提高算法的查询效率。

2.1 建立DAG索引

定义1(DAG图) 将给定的图g进行图分解，得到具有如下特点的结构图：

(1)任一节点P都是图g的子图；

(2)对节点P和Q而言，若P⊂Q，存在P指向Q的有向关系，则该分解称为(图的分解)DAG图。

图1给出了一个完全连通图进行分解后的DAG图。DAG图中有且只有一个节点ABBC代表图G，有且只有一个节点表示空图。图的分解DAG通过路径反映出节点的尺寸大小和层次关系。如AB、AC、BB、BC具有相同的尺寸，即同一层上的节点具有相同的顶点数，而不同层之间则具有包含和被包含的关系。

Figure 1 Decomposition of graph in DAG图1 图分解DAG

本文对给定的查询图q和图数据集G进行DAG图分解，得到的DAG图将按照图的标准代码[11]进行编码，采用哈希表完成索引的存储与构建。具体构造DAG过程如下：

(1)选定一个空节点作为DAG起始的根节点。

(2)记特征图中不重复的任意一个节点为根节点的下一级节点，在分解过程的每条路径上，下一层总是比上一层多出一个节点。

(3)连接节点间有边的节点，每次只增加一个节点，扩展DAG。对于相连的两个节点P和Q，如果P⊂Q，那么不存在P′使得P⊂P′⊂Q。所以，当连接节点中包含图节点的总数就是这个节点的大小。

(4)直至所有节点都包含在DAG中。

其算法步骤如下：

算法1DAG索引的建立DAGindex(G)

输入：G∥输入图数据G

输出：DAG图、Ht/*输出DAG图，编码后的Hash表Ht*/

1:DAG=∅,Ht=∅;

2: for eachgi∈G

3: ifgi∉DAG

4:DAG=DAG∪gi;

5:Ht⟸Hash(gi);/*将gi哈希码加入Hash表Ht中*/

6:Decom(gi,DAG,Hash);

7: end if

8: end for

9:return (DAG,Ht);

Decom(gi,DAG,Ht)∥图的分解函数

1: for eachvingi∥gi中的每个节点

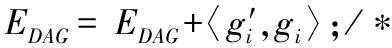
8: end if

9: end for

2.2 最小生成树集

如图2所示，查询图q为图2a，对于q的三个子图图2b～图2d都存在两条边的缺失。因此，对子图2b～图2d而言，它们都利用了同一个公共最小生成树[12]，如图中加粗黑边所示。通过图2可知，对于任何与图2b～图2d三个子图精确匹配的目标图也必定和该最小生成树匹配。由此可知，对于查询图q，得到其最小生成树集并对最小生成树进行满足条件θ的扩展，容易得到查询图q的子图。

Figure 2 Minimum common spanning tree图2 公共最小生成树

对于一个给定查询图q的图数据集G，首先从查询图q中得到其最小生成树集qt；其次，对qt进行扩展，使其能够覆盖最小生成树并且与q的编辑距离不超过θ条边，即对q的所有连通子图而言，任意一个q′都是qt的超图。

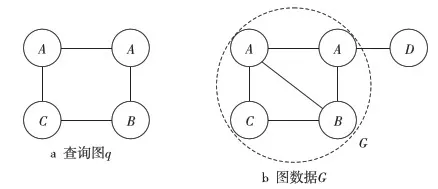
Figure 3 Query graph q & graph data G图3 查询图q与图数据G

如图4所示，图4a为图3中q的精确匹配图，同样也可认为是查询图q中满足θ≤1的近似图。通过该精确匹配，可以得到生成子图图4b～图4e。由于其均为图4a的连通子图，并且都缺少一边，因此可认为是满足θ=1时q的近似子图。

Figure 4 Similary graph of query graph q (θ=1)图4 q的近似子图(θ=1)

本文采用Kruskal算法得到最小生成树集qt。

首先，利用Kruskal得到一棵最小生成树，将其边权相同的边置入一个边组。根据同一个图的不同最小生成树之间度数相同的性质[7]：

(1)每个边组中所需的边的个数一样；

(2)对完成Kruskal运算后的边组所形成的联通分量相同。Kruskal运算对于同样具有i(i=1,…,n,n为正整数)条边的边组，其所形成的联通分量具有相同数目。

其次，利用DFS枚举所有可能的相同边组，然后依次相乘。

最后，输出全部最小生成树，形成最小生成树集。

在最小生成树集的基础上，通过对其进行满足θ条件的子图扩展，得到子图集合。生成扩展子图算法如下：

算法2生成扩展子图Gensub(qt,θ)

输入：qt∥最小生成树集

θ∥近似图编辑距离;

输出：SUBset。

1:for eachqtiinqt

2:sub=qti;

3: for eachviinqti

4: if |E(sub)|-|E(qti)|<θ

5: ifviandvjnot connected/*vi、vj为sub中的节点*/

6:E(sub)=E(sub)+(vi,vj);

7: end if

8:SUBset=SUBset∪sub;

9: end if

10: end for

11:returnSUBset;∥返回扩展子图集合

2.3 DAG近似查询

对查询图q近似查询之前，同样需要将生成的扩展子图进行DAG分解，这样方便通过图编码找到查询图与目标图之间的公共子图作为起点，逐步找到满足条件θ的近似结果集。

如图5所示，DAG图中有且只有一个节点ABBC代表图gi，有且有一个节点表示空图。图的分解DAG通过路径反映出节点的尺寸大小和层次关系。如AB、AC、BB、BC具有相同的尺寸，即同一层上的节点具有相同的顶点数，而不同层之间则具有包含和被包含的关系。

Figure 5 Decomposition of graph in DAG图5 图分解DAG

因此，若q的扩展子图sub的节点为BC，则通过图编码是否相同进行子图同构判断，可以迅速通过索引定位到DAG中，得到近似图ABC、BBC、ABBC。

生成候选集算法如下所示，通过枚举得到满足阈值θ的候选集，此时只需将候选集中出现的重复项过滤即可得到近似结果集。

算法3生成候选集CandidateSearch(DAG,SUBset,θ)

输入：DAG∥查询图q和图数据G的图分解

SUBset∥扩展子树

θ∥近似图编辑距离;

输出：近似结果集。

1:candidate=∅;

2:for eachsubinSUBset

3: ifsubexist inDAG

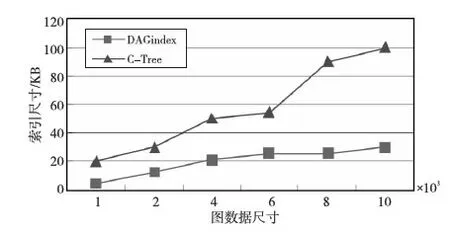
4: iflevel

5:candidate=candidate∪sub’schildren;/*从DAG中得到当前节点的孩子节点*/

6: nextlevel;

7: end if

8: end if

9:end for

10:returncandidate;

3 实验结果及性能分析

3.1 实验环境

本文提出方法的实验环境是Intel CPU Pentium T4500，主频为2.3 GHz，内存DDR3 2 GB，硬盘320 GB，操作系统为Windows XP professional sp3；所有算法均用C++在VC 6.0环境下实现。

3.2 实验数据

实验数据采用真实数据和模拟数据。真实数据来自于DTP(Developmental Therapeutics Program)提供的化合物数据集合[13]。该数据集合包含10 000个图，每个图平均有5.6个顶点，其中顶点表示一个化合物分子，边表示两个分子之间的连接。模拟数据集使用GraphGen生成，可生成类似“D10kT20i10V5E5”的文件名来记录的数据，它表示生成图的总数为10 000个，图的平均尺寸为20条边，生成图的平均尺寸为10条边，图节点的标号个数是5个，图边的标号个数是5个。

3.3 实验结果及性能分析

C-Tree利用启发式图映射方法来判断编辑距离，进而得到近似图。但是，该算法仅仅能查询到k个最近的近似结果。对于当前信息数据的复杂化，其查询结果及效率并不理想；而DAGindex算法属于范围查询则返回用户定义的某个范围内的全部结果。时间复杂度对比来看，C-Tree的复杂度为O(2n·2n)，而DAGindex复杂度为O(nlogn·2n)，查询效率有一定的提高。实验分别从索引构建性能和实验结果集的查准率进行比较，比较结果如下所述：

(1)索引构建比较：将DAGindex算法与C-Tree的索引构建用真实数据集进行比较分析，分别取真实数据集为1 KB、2 KB、4 KB、6 KB、8 KB和10 KB进行测试。图6中X轴表示图数据库的大小尺寸，Y轴表示生成的索引尺寸大小，单位为KB。而在图7中Y轴用来表示生成索引的时间，单位为ms。从图6和图7中的数据曲线比较可知，两种算法的索引大小以及构建索引的时间均和图数据中的顶点数成线性增长关系。但是，随着图尺寸逐渐增大，本文算法中的索引构建尺寸及时间均保持在一个较平稳的增长，说明其对大图数据也能生成质量较高的索引。同时，由图6和图7可知，本文算法的曲线图线条比C-Tree要低，说明在本文算法构建索引性能上效率更高。

Figure 6 Comparison of index size图6 索引尺寸的比较

Figure 7 Comparison of index construct time图7 索引构建时间的比较

(2)结果集比较：本文采用真实数据集进行，取查询图q的尺寸分别划分为5、10、15、20、25，采用尺寸为10 000的图数据进行实验。阈值θ决定查询的近似程度，当θ=0时，近似查询的实质就是精确查询。因此，此处用DAGindex与gindex进行测试对比，用实验测试文章算法的查准率。如图8所示，X轴表示查询图q的尺寸大小(图q的顶点数)，Y轴表示查询结果集的尺寸大小(图个数)。由图8可知，DAGindex曲线随着q尺寸的增大，其候选集尺寸也随之减小。与gindex的候选结果集基本接近，表明了算法的有效性。

Figure 8 Comparison of result size图8 结果集尺寸比较

4 结束语

图近似查询具有广泛的应用背景，已成为图数据领域中的热点。本文讨论了近似查询中存在的信息不全等问题，提出了一种基于图分解的近似查询方法。实验表明，利用该方法可以有效减少查询时间，降低了计算复杂度，能够得到准确的候选集，从而提高查询效率。随着图数据信息量的急剧膨胀，大图数据中的近似查询方法研究将成为今后研究中的重点。

[1] Shasha D，Wang J T L，Giugno R．Algorithmics and applications of tree and graph searching[C]∥Proc of the 21st ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, 2002:39-52.

[2] Yan X，Yu P S，Han J. Graph indexing：A frequent structure-based approach[C]∥Proc of the 2004 ACM SIGMOD International Conference on Management of Data, 2004:335-346.

[3] Zou L, Chen L, Yu J X, et al. A novel spectral coding in a large graph database[C]∥Proc of the 11th International Conference on Extending Database Technology (EDBT), 2008:181-192.

[4] Williams D W, Huan J, Wang W. Graph database indexing using structured graph decomposition[C]∥Proc of IEEE 23rd International Conference on Data Engineering, 2007:976-985.

[5] Jiang H, Wang H, Yu P S, et al. GString：A novel approach for efficient search in graph databases [C]∥Proc of IEEE 23rd International Conference on Data Engineering, 2007:566-575.

[6] Chen C, Yan X, Yu P S, et al. Towards graph containment search and indexing[C]∥Proc of the 33rd International Conference on Very Large Data Bases, 2007:926-937.

[7] Zhang S, Li J, Gao H,et al. A novel approach for efficient supergraph query processing on graph databases[C]∥Proc of the 12th International Conference on Extending Database Technology, 2009:204-215.

[8] Wang Fang, Jin R, Agrawal G, et al. Graph and Topological Structure Mining on Scientific Articles[C]∥ Proc of the 7th BIBE, 2007:1318-1322.

[9] Zou Xiao-hong,Chen Xiao,Guo Jing-feng,et al. An improved algorithm for mining closegraph[J]. ICIC Express Letters,2010,4(4):1135-1140.

[10] He Hua-hai,Singh A K.Closure-tree:An index structure for graph queries[C]∥ Proc of the 22nd ICDE, 2006:38.

[11] Huan Jun, Bandyopadhyay D, Wang Wei, et al. Comparing graph representations of protein structure for mining family-specific residue-based packing motifs[J]. Journal of Computational Biology, 2005, 12(6):657-671.

[12] Zhu Gao-ping, Lin Xue-min, Zhu Ke, et al. TreeSpan:Efficiently computing similarity all-matching[C]∥Proc of 2012 SIGMOD, 2012:529-540.

[13] DTP chemical data [EB/OL]. [2012-11-15]. http:∥dtp.nci.nih.gov/docs/aids/aids_data.html.