一种新的基于直觉模糊Petri网的模糊推理算法*

申蔓蔓，乐晓波，周恺卿

(1.长沙理工大学计算机与通信工程学院，湖南 长沙 410114；2.马来西亚理工大学计算学院，马来西亚UTM士古来 柔佛洲 80310)

1 引言

传统Petri网PN(Petri Nets)理论不能处理非确定信息，使得Petri网在建模、处理和分析不确定系统时缺乏柔性。为了克服这一问题，Lipp L L在1984年提出模糊Petri网的概念。作为Petri网理论与模糊集合理论的有机结合的一种高级拓扑结构，模糊Petri网在不确定知识的表示和推理领域得到了广泛的应用。近年来学者于不同研究背景提出了不同的模糊Petri网模型和相应的模糊推理算法[1～6]。文献[1]给出了带标识的模糊Petri网进行模糊推理，该方法采用了一种改进的相似度，因此计算出推理结果的意义更加明晰。文献[2]提出了基于区间值的直觉模糊Petri网IFPN(Intuitionistic Fuzzy Petri Nets)模型，使直觉模糊推理在理论上得以实现。文献[3]基于直觉模糊Petri网理论，建立了空战战术决策模型，引入非隶属度函数，在处理不确定信息时具有更强的表现能力。文献[4]提出的基于直觉模糊Petri网的意图识别方法,在推理过程中充分发挥Petri网的动态并行推理能力,使得推理更加高效。文献[5]提出了一种基于模糊故障树的模糊Petri网模型，更适合对事故现场进行诊断。文献[6]基于模糊Petri网的电动机轮子故障诊断，表明模糊Petri网有一个简单的结构、良好的表达断层和模糊推理的能力。

但是，随着对实际问题认识和研究的不断深入，传统模糊集合理论不能完整表达所研究问题的所有信息这一缺陷在实际应用过程中越来越突出[7]。因此，在以模糊Petri网为工具进行知识表示和模糊推理的过程中，由于难以获得足够的信息导致不能获得满意的推理结果。为了克服这一问题，本文试图将具有较强的表达能力、处理不确定的信息能力的直觉模糊集合引入模糊Petri网理论，给出直觉模糊Petri网(IFPN)的形式化定义[8]，并在基于该模型的推理过程中引入库所重排策略，提出一种新的基于IFPN模型的库所重排策略的推理算法，有效简化模糊推理过程。最后，通过实例检验此算法的可行性和有效性。

2 基本定义

2.1 算法所涉及的相关定义

直觉模糊集是保加利亚学者Tanassov K A[9]在模糊集基础上提出的新概念，增加了一个新的属性参数—非隶属度函数，以一个区域值代替了隶属度，具有更强的模糊描述能力。直觉模糊Petri网是在Petri网的基础上扩展而来的，它应用的出发点是基于其知识表达和逻辑推理功能。直觉模糊理论在原有Zadeh模糊集理论的基础上引入直觉模糊集定义，进而可以描述“非此非彼”的“模糊概念”[10]。

定义1(直觉模糊集合) 设X为论域，则X上的一个直觉模糊集合A为：

A={〈x,μA(x),νA(x)〉|x∈X}

其中,μA(x):X→[0,1]，νA(x):X→X[0,1]，且0≤μA+νA≤1,∀x∈X,μA(x)表示x对A的隶属程度，νA(x)表示x对A的非隶属程度。

定义2(直觉模糊关系) 设X和Y是普通、有限非空集合的论域。定义在直积空间X×Y上的直觉模糊子集称为从X到Y之间的二元直觉模糊关系。记为：

R={〈(x,y),μR(x,y),νR(x,y)〉|x∈X,y∈Y}

其中,μR:X×Y→[0,1]和νR:X×Y→[0,1]满足条件0≤μR(x,y)+νR(x,y)≤1,∀(x,y)∈X×Y。

定义3(1)乘法算子⊙：

C=A⊙B⟺C=(μA(x)·μB(x),

νA(y)+νB(y)-νA(y)·νB(y))

(2)加法算子⊕：

C=A⊕B⟺Cij[max(μA(x),μB(x)),

min(νA(y),νB(y))]

文献[11]对乘法算子⊙与加法算子⊕做了较详细的讨论。

2.2 IFPN的形式定义及相关规则

为使直觉模糊推理更加方便，本小节在直觉模糊集合的基础上给出直觉模糊Petri网的定义及其形式化表示。

定义4直觉模糊Petri网可以用一个六元组来表示：

IFPN=(P,T,I,O,M,τ)

其中:

(1)P=PU∪PQ∪PD为IFPN中有限库所集合，每一个库所对应着一个命题。为使直觉模糊推理更高效，本文给出了库所的重排：

P=PU∪PQ∪PD

其中,PU={p1,p2,…,pm1}代表初始库所，PQ={q1,q2,…,qm2}代表中间库所，PD={d1,d2,…,dm3}代表结论库所，m=m1+m2+m3为总库所数。

(2)T={t1,t2,…,tm}为IFPN中变迁的集合，每个变迁对应一个规则。

(3)In×m={aij|pi∈P,tj∈T}，i=1,2,…,n;j=1,2,…,m,其中aij∈[0,1]表示库所pi到变迁tj的输入权重。

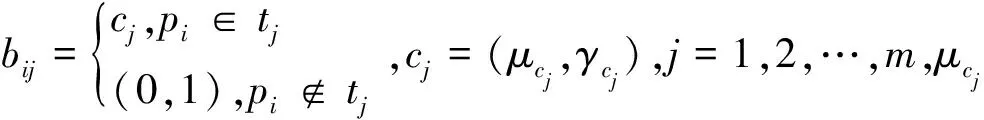
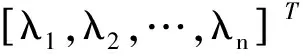
(6)S:P→[0,1]为库所P的一个关联函数，表示库所P对应的命题的模糊标识值，初始标识S0=[S0(p1),S0(p2),…,S0(pn)]T，其中S0(pi)为直觉模糊数(u0i,y0i)。

用直觉模糊Petri网的变迁来表示直觉模糊产生式规则，变迁的输入表示规则的前提，变迁的输出库所表示规则的结论，通过阈值来控制变迁的发生，并用变迁的置信度表示模糊规则的可信度。与普通模糊Petri网产生式规则不同的是，直觉模糊Petri网产生式中的这些量都是用直觉模糊集表示的，具体模型有以下三种类型[11]：

类型1简单直觉模糊产生式规则。

IFaTHENb (CF=c)

其中，a是前提命题，b是结果命题，p1为变迁t的输入库所，p2为变迁t的输出库所，c为规则的可行度，M1表示输入库所中的标识，M2表示输出库所中的标识。该类型直觉模糊Petri网表示如图1所示。

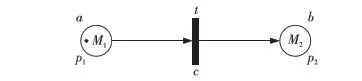
Figure 1 Corresponding IFPN model of simple IFPR图1 简单IFPR的IFPN表示

类型2合取直觉模糊产生式规则。

IFa1ANDa2AND…ANDanTHENak( CF=c, τ)

其中前提命题a1，a2，…，an分别由库所p1，p2，…，pn代替，结果命题由ak代替，该类型的直觉模糊Petri网表示如图2所示。

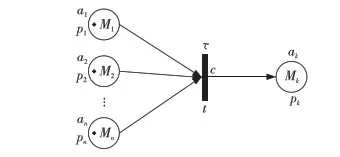
Figure 2 Corresponding IFPN model of ‘and’ IFPR图2 合取式IFPR的IFPN表示

类型3析取直觉模糊产生式规则。

IFa1ORa2OR…ORanTHENak(CF=c1, CF=c2,…, CF=cn)

该类型的直觉模糊Petri网表示如图3所示。

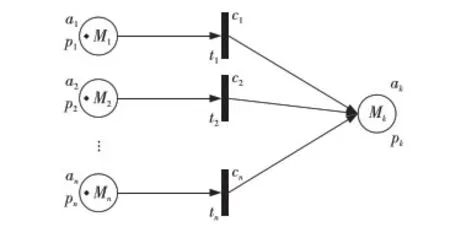
Figure 3 Corresponding IFPN model of ‘or’ IFPR图3 析取式IFPR的IFPN表示

3 基于IFPN模型的推理算法

直觉模糊Petri网(IFPN)将直觉模糊集合引入模糊Petri网理论，在基于该模型的推理过程中引入库所重排策略，并利用可激活变迁判断计算公式对推理的每一步进行可激活变迁判断，提出一种新的基于IFPN模型的库所重排策略的模糊推理算法，有效简化了模糊推理过程，提高了算法的时间效率。其算法处理过程如下。

在IFPN模型中，每一步推理过程的模型的有关数据描述：

输入：输入矩阵Ii×j、变迁阈值τj、初始标识向量S0：

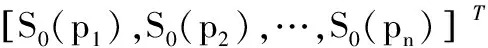
输出：输出矩阵Oi×j、库所的标识向量S：

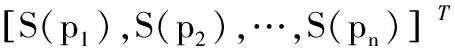
步骤1初始化，令K=0，I=(0,1)，此处(0,1)为每个元素均为直觉模糊数(0,1)的矩阵。

步骤2判断重排后的库所对应的变迁(初始库所PU对应变迁和中间库所PQ对应的变迁)能否发生。判断变迁是否可激活的计算公式如下：

如果

(1)

则变迁tj可激活。

判断有无可激活变迁，若无变迁可激活，则第K步推理结束，跳过步骤3和步骤4，进入步骤5；否则，激活可激活变迁tj，继续执行步骤3。

步骤3计算变迁tj激活后各个库所的可信度:

合取：

(2)

析取：

(3)

步骤4更新所有库所可信度:

SK+1(pn)=SK(pn)⊕SK+1(pn)

(4)

步骤5判断推理过程是否还有第K+1步，若是，则令K=K+1，返回步骤2；否则推理结束。

上述算法在采用库所重排策略的过程中，步骤2对第K步系统中可激活的变迁进行有效判断，每一步只对可激活变迁进行计算处理，从而避免了对系统中全部变迁进行计算，简化了推理过程，节省了推理时间。

上述算法的框图描述如图4所示。

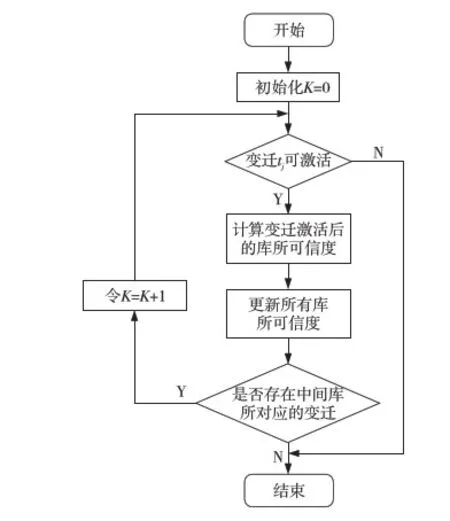
Figure 4 Flowchart of the proposed reasoning algorithm using IFPN图4 基于IFPN模型的推理算法框图描述

4 实例分析

这里采用文献[8]中汽车发动机故障诊断的实例以验证本文所提出的算法的可行性和有效性，为编程方便，本文将原实例中库所p5和p6的位置交换，使编程中的参数取值能连续。

关于汽车发动机故障诊断的推理规则如下：

R1：IFV1(0.7)ANDV2(0.2)ANDV3(0.3)THEN(τ1=(0.4，0.55)) V6(CF=(0.8，0.18))

R2：IFV1(0.7)ANDV4(0.3)THEN(τ2=(0.4，0.58)) V7(CF=(0.8，0.15))

R3：IFV5(1.0)THEN(τ3=(0.3，0.66)) V8(CF=(0.9，0.1))

R4：IFV6(0.7)THEN(τ4=(0.3，0.67)) V8(CF=(1.0，0.0))

其中，V1表示蓄电池电压过低，V2表示点火时间过晚，V3表示进气系统漏气，V4表示节气门不能关闭，V5表示发动机回火，V6表示发动机转数不良，V7表示发动机加速不良，V8表示发动机不能启动。

该组规则的IFPN推理模型如图5所示。

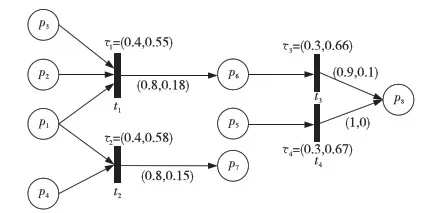
Figure 5 IFPN model of the case study图5 IFPN推理模型

推理过程如下：

首先，令K=0，I=(0，1)，根据IFPN模糊推理算法输入输入矩阵Ii×j，输出矩阵Oi×j、初始标识S0以及变迁阈值τ：

输出矩阵Oi×j=

初始标识S0=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0,1) (0,1) (0,1) ]T

变迁阈值τ= [(0.4,0.55) (0.4,0.58) (0.3,0.66) (0.3,0.67)]T

(1)利用式(1)判断变迁t1、t2可激活，利用式(2)～式(4)计算得：

S1=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0.504,0.478) (0.752,0.2) (0,1)]T

(2)利用式(1)判断变迁t3可激活，利用式(2)～式(4)计算得：

S2=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0.504,0.478) (0.752,0.2) (0.454,0.53)]T

(3)利用式(1)判断无变迁可激发，因此推理结束，此时，IFPN输出的库所标识向量为：

S2=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0.504,0.478) (0.752,0.2) (0.454,0.53)]T

从推理结果可以看出，隶属度最大并且非隶属度最小的库所的标识为p7=(0.752,0.2)，这个结果与表1所示文献[8]中采用的推理算法计算的结果一样，但其计算过程明显简洁。文献[8]中步骤3为判断各个变迁的状态转移函数值是否大于之前的最大状态转移函数值，即每次计算变迁转移函数值后，都要重新判断各个变迁的状态函数值是否大于之前的状态函数值；而本文提出的算法因采用了库所重排策略有效地避免对未激发变迁的判断，从而大大节省了推理时间，提高了计算效率。

Table 1 Simulation results of reference[8]

5 结束语

本文提出了一种基于直觉模糊Petri网的库所重排策略及其相关的模糊推理算法，有效地提高了推理速度和推理效率。从表1可以看出，与文献[8]的推理算法比较，本文所设计的推理算法可得到同样精确的结果，本文的推理过程只有五步而文献[8]有八步，且文献[8]每次计算一个变迁转移函数值后都要重新考虑所有变迁是否发生，而本文只需判断此时还未产生的变迁是否能被激活，从而有效地简化了推理过程，节省了推理时间，降低了算法的时间复杂度。由此可见，本文所提出的基于IFPN模型的推理算法为模糊推理的研究提供了一个新的途径，此算法的可行性与正确性已在VisualC++6.0环境下得到了验证。

[1]SunXiao-ling,WangNing,LiangYan,etal.FuzzyreasoningbyusingmarkedfuzzyPetrinets[J].ComputerEngineering&Science, 2012, 34(3):152-157.(inChinese)

[2]HanGuang-chen,SunShu-dong,SiShu-bin,etal.ResearchonfaultdiagnosissimulationbasedonfuzzyprobabilityPetrinetssystem[J].ComputerIntegratedManufacturingSystems, 2006, 12(4):520-525.(inChinese)

[3]ZhangYing,YangRen-nong,WuMeng,etal.Aircombattacticsdecision-makingbasedonintuitionisticfuzzyPetrinet[J].ComputerEngineeringandApplications, 2012, 48(30):224-228.(inChinese)

[4]ZhouChuang-ming,ShenXiao-yong,LeiYing-jie.ResearchoffoeintentionrecognitionmethodbasedonintuitionisticfuzzyPetrinet[J].ComputerApplication, 2009, 29(9):2464-2467.(inChinese)

[5]LuQ,HuangG,ZhuH.FuzzyanalysisofaccidentsdiagnosisbasedonfuzzyPetrinet[J].InternationalJournalofSystemsControl, 2007, 2(3):228-236.

[6]TianxuJ,GeZ.AmethodforfaultdiagnosisintestsystemofelectricmotorwheelsbasedonFuzzyPetrinet[C]∥Procofthe31stControlConference(CCC), 2012:5240-5244.

[7]QiaoF,WuQ,LiL,etal.AfuzzyPetrinet-basedreasoningmethodforrescheduling[J].TransactionsoftheInstituteofMeasurementandControl,2011,33(3-4):435-455.

[8]SunXiao-ling,WangNing.WeightedintuitionisticfuzzyreasoningbasedonintuitionisticfuzzyPetrinets[J].ComputerEngineeringandApplications, 2013, 49(4):50-53.(inChinese)

[9]ShenX,LeiY,LiC.IntuitionisticfuzzyPetrinetsmodelandreasoningalgorithm[C]∥Procofthe6thInternationalConferenceonFuzzySystemsandKnowledgeDiscovery, 2009:119-122.

[10]LiaoWei-zhi,GuTian-long,LiWen-jing,etal.ModelingandschedulingforfuzzyflexiblemanufacturingsystembasedonhybridPetrinets[J].ComputerIntegratedManufacturingSystems, 2008, 14(11):2134-2141.(inChinese)

[11]VardevaI,GochevV.Calculationofestimationsofmessagesbygeneralizednetsandintuitionisticfuzzytruthvalues[C]∥Procofthe6thIEEEInternationalConferenceonIntelligentSystems, 2012:242-245.

附中文参考文献：

[1] 孙晓玲,王宁,梁艳,等.应用带标识的模糊Petri网的模糊推理[J].计算机工程与科学,2012,34(3):152-157.

[2] 韩光臣,孙树栋,司书宾,等.基于模糊概率Petri网系统的故障诊断仿真研究[J].计算机集成制造系统,2006,12(4):520-525.

[3] 张滢,杨任农,邬蒙,等.直觉模糊Petri网的空战战术决策[J].计算机工程与应用,2012,48(30):224-228.

[4] 周创明,申晓勇,雷英杰.基于直觉模糊Petri网的敌意图识别方法研究[J].计算机应用,2009,29(9):2464-2467.

[8] 孙晓玲,王宁.基于直觉模糊Petri网的加权直觉模糊推理[J].计算机工程与应用,2013,49(4):50-53.

[10] 廖伟志,古天龙,李文敬,等.模糊柔性制造系统的混杂Petri网建模与调度[J].计算机集成制造系统,2008,14(11):2134-2141.