三相电压型PWM整流器最优H∞鲁棒控制研究

杜运超，邵天章，谷志锋

（军械工程学院车辆与电气工程系，河北石家庄050003）

三相电压型PWM整流器最优H∞鲁棒控制研究

杜运超，邵天章，谷志锋

（军械工程学院车辆与电气工程系，河北石家庄050003）

基于现有三相电压型PWM整流器双环PI控制的不足，采用非线性控制理论，对电流内环进行改进，提出了一种反馈线性化最优H∞鲁棒控制策略。首先对三相电压型PWM整流器的dq模型进行分析，选取状态变量、输出变量，建立仿射非线性系统模型，然后对模型进行状态反馈精确线性化，得到解耦的精确线性化系统，通过解Riccati不等式，最终得到最优控制规律。仿真结果表明：该控制方法能使系统在固定范围内强干扰和参数摄动的状态下实现功率因数整流，并且保持稳定的输出直流电压，可以为战场条件下移动电站应急供电提供有效技术支持。

三相电压型PWM整流器；反馈线性化；双环控制；最优H∞鲁棒控制

PWM整流器是实现武器装备全电化、船舶综合电力系统等直流组网的关键环节，并对于提高供电性能和有效利用有限空间具有重要的意义；在野战条件下，当单个军用电站受到攻击或出现故障而不能正常供电时，如何实现多种电压、频率制式的军用电站快速组网，并构建直流输电网，对于实现用电装备的逆变应急供电同样具有重要军事意义。近年来，许多学者在PWM整流器的控制算法改进等多个方面进行了有效的研究［1］。

文献［2-3］对电流环采用前馈解耦控制策略后，基于PI的控制理论，设计了双闭环的控制系统。文献［4-5］分别从预测控制和神经网络控制2个方面建立了三相电压型PWM整流器的智能控制系统，取得了较好的实验结果。然而以上控制方式中，部分采用PI控制方式，忽略了系统本身的非线性特性，不能保证系统的快速响应和在大范围扰动的情况下保持稳定；部分采用智能控制和其他控制方式相结合的方法，导致控制算法过于复杂，不能较好地应用于工程实践。

本文基于三相电压型PWM整流器的非线性数学模型，对传统双环PI控制系统的电流内环进行改进，采用状态反馈线性化的方式使电流内环实现线性解耦，保证了控制系统的本质非线性特性。为降低诸如输入电压波动、负载突变等外部干扰和输入控制器的参数误差、测量误差等内干扰对输出的不利影响，对解耦后的系统采用非线性鲁棒控制的设计方法，建立了相应的控制规律，使系统的动态响应速度和鲁棒性得到较好提升。最后通过仿真验证了控制系统的优越性，该整流器能够为战场条件下的武器装备提供有效的应急电力支持。

1 三相电压型PWM整流器的数学模型

三相电压型PWM整流的拓扑结构如图1所示。

图1 三相电压型PWM整流器主电路拓扑结构Fig.1Main circuit topology structure of the three⁃phase PWM rectifier

图1中，ea,eb,ec为交流侧相电压；ia,ib,ic,为交流侧各相电流；udc代表直流侧电压；ua,ub, uc为整流器交流侧输入电压；iL为负载电流。

在dq坐标系下三相电压型PWM整流器模型［6］为

2 非线性鲁棒控制

2.1 电流内环控制系统模型

首先，对式（1）前2行进行变换，选取状态变量和输入变量分别为

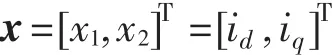
同时设定输出变量为

式中：idref，iqref分别为交流电网侧的三相电流经dq变换后在d轴和q轴的分量。

由于电路中电容、电感参数和理想设定值在运行的过程中不能保持绝对一致，且输入电压存在小范围波动，不能维持稳定的数值，为将所有的干扰和不确定的因数归结为一项［8-9］：取干扰项

由此建立如下仿射非线性系统模型：

其中

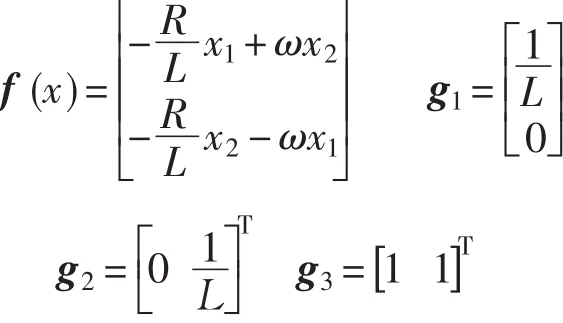
2.2 基于反馈精确线性化的电流内环控制

为了得到线性解耦的控制系统，首先验证式（2）的非线性系统是否满足精确反馈线性化条件：

通过将式（3）的值带入判定矩阵中，可知矩阵[g1(x)g2(x)adfg1(x)adfg2(x)]的秩为2，和系统的维数n相等。

当系统维数n=2时，可知向量场集合D= { } g1(x)g2(x)adfg1(x)adfg2(x)是对合的，由此系统可实现精确线性化。在系统满足状态反馈精确化的条件下，对给定输出通过Lie导数计算系统的相对阶：

由式（4）知矩阵的奇异值不等于0，因此系统的关系度集合为r={r1,r2}={1,1}，并且关系度总数与系统的维数相等r=n。根据反馈精确线性化理论选择坐标映射为

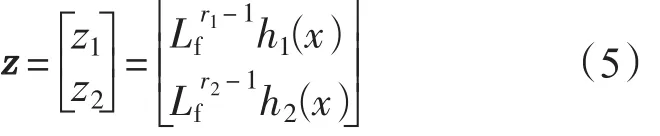
选择相应的控制向量为

相应的干扰项经过坐标映射后变为

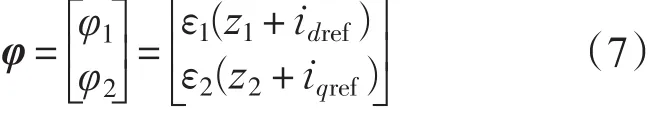
φ1和φ2为干扰项经过坐标映射式（5）变换后得到的表达式，并且干扰项由于只和参数相关，因此通过坐标映射后也实现了相应的线性解耦，由此系统的所有量经过坐标映射后，得出了非线性解耦后的表达式，结合式（2）、式（5）、式（6）、式（7）得到如下线性解耦系统：

由于式（8）中不显含状态变量z，对其进行变换后得到如下标准化系统：

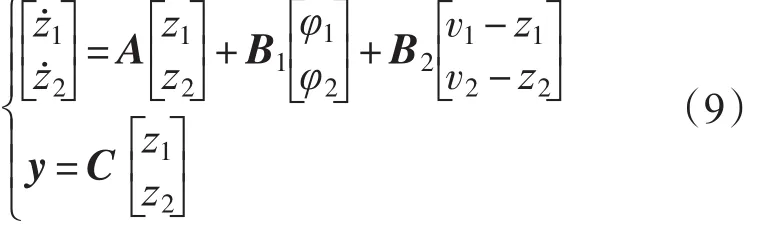
其中

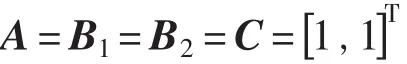
式（9）中的v1和v2由控制系统所要达到的控制效果决定，为保证式（9）的线性解耦系统在干扰输入到输出的L2增益最小的前提下，在平衡点z0=[0,0]T上稳定，求解如下所示Riccati不等式：

存在非负解P*，则此时最优的控制策略v*为

相应的最坏可能干扰为

经计算并最终选择P*的最优解为

结合式（6）、式（12）、式（13）可知原非线性系统的最优控制率为

式中：K=9×105L。

取式（14）中的第1项进行变换可得：

当相电压出现突变或者电路参数R,L与设定值存在误差时，K(id-idref)也会出现突变，并且变化的数量级比其他项都要大，从而使干扰对系统产生的不利影响得到抑制，同理式（14）中第2项也实现了干扰的抑制，由此本文提出的控制规律实现了系统的鲁棒控制。

其控制模型如图2所示。

3 仿真和试验研究

为验证本文所建立的控制系统的可行性和有效性，在Matlab/Simulink环境下对三相电压型PWM整流器进行仿真实验。仿真参数为：相电压有效值Us=110 V，交流侧等效电阻R= 0.1 Ω，交流侧电感L=10 mH，直流侧稳压电容C= 5 000 μF，直流母线设定电压U*dc=500 V，整流器开关频率为f=2 000 Hz，初始负载R=100 Ω。为了直观反映改进后的控制规律的优越性，下面分为以下3个方面对现有双环PI控制和外环PI控制与内环非线性鲁棒控制相结合的控制效果相比较。

采用双环PI控制时，电压外环和电流内环的参数分别为：Kup=3，Kui=15和Kip=15，Kii=30；采用改进后的控制系统时，电压外环控制器的PI参数为：Kp=1，Ki=80，电流内环采用非线性鲁棒控制，其控制方式为

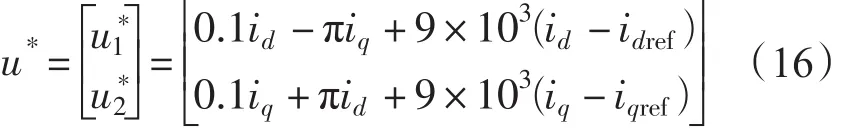
为了方便比较交流侧相电压与相电流的关系，将0.1倍交流侧相电压测量瞬时值与相电流瞬时值相比较，并反映到仿真图像中。

3.1 PWM整流器启动动态响应

额定负载条件下PWM整流器启动后，双环PI控制系统和非线性鲁棒控制系统下直流响应、交流侧相电压与相电流的关系分别如图3、图4所示。

图3 PI控制方式下的启动响应Fig.3The starting response in the PI control method

图4 非线性鲁棒控制方式下的启动响应Fig.4The starting response in the robust control

比较图3、图4可知：改进后的控制系统能使输出电压较快实现在500 V处稳定，并且稳定后可实现精确单位因数整流。

3.2 交流侧电压突变时，系统的动态响应

为验证系统在交流侧电压出现大范围扰动时，系统依然能保持稳定。额定负载条件下交流侧相电压在0.6 s时由110 V突变为55 V，维持0.2 s后，在0.8 s时由55 V突变为220 V，两种控制方式下系统的直流侧电压响应、状态变量id如图5、图6所示。

图5 电压突变时PI控制方式下的状态变化曲线Fig.5The state change curves in the PI control method on the condition of voltage sudden change

图6 电压突变时非线性鲁棒控制方式下的状态变化曲线Fig.6The state change curves in the robust control on the condition of voltage sudden change

比较图5、图6可知，不论交流侧电压在一定范围内如何突变，改进后的控制系统都能使直流侧电压更快更好地实现稳定，并且在运行过程中状态变量的震荡较小，使系统更易于保持稳定。

3.3 电感参数摄动时，系统的动态响应

启动三相电压型PWM系统时，输入电感由系统设定的L=10 mH变为L=40 mH后，比较两种控制方式下直流侧电压响应、状态变量id,iq的变化曲线如图7、图8所示。

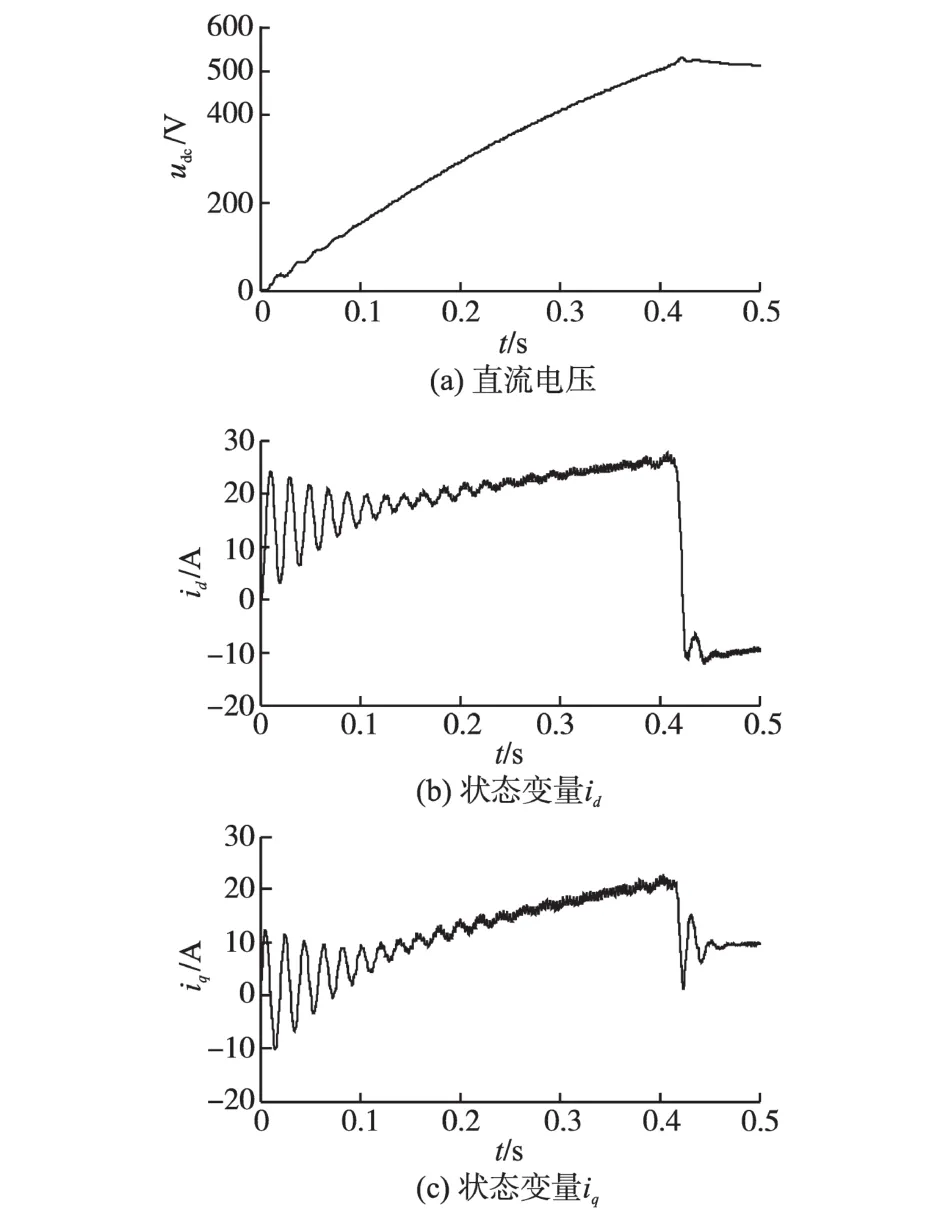
图7 电感参数摄动时PI控制方式下的状态变化曲线Fig.7The state change curves in the PI control method on the condition of inductance change

图8 电感参数摄动时非线性鲁棒控制方式下的状态变化曲线Fig.8The state change curves in the robust control on the condition of inductance change

比较图7、图8可知，改进后的控制系统能使直流电压在超调后快速实现稳定，并且状态变量id在系统稳定后就实现了在设定值处稳定，iq也实现了摄动最小化。

4 结论

针对三相电压型PWM整流器的模型，基于现有双环PI控制的基础上，对电流内环进行改进，提出了反馈线性化最优H∞鲁棒控制策略，对系统在固定范围内外部干扰和内部扰动的情况下进行了深入分析。通过理论分析和仿真验证得到：提出的控制系统在保证系统稳态启动的情况下，能实现直流电压的快速稳定；保证在交流侧电压存在剧烈震荡、电路参数出现一定范围内摄动时，依然能保持系统的稳定和功率因数整流。该控制方法适合作为系统存在强干扰，交流端电压变化大的三相电压型PWM整流的应用场合。

［1］程启明，程尹曼，薛阳，等.三相电压型电压源型PWM整流器控制方法的发展综述［J］.电力系统保护与控制，2012，40（3）：145-154.

［2］Ye Y，Kazerani M.A Novel Modeling and Control Method for Three⁃phase PWM Converters［C］//PESC.2001 IEEE 32th An⁃nual.2001，1：102-107.

［3］李龙，牛聪，贪洪奇，等.三相电压型PWM整流器的自适应PI控制研究［J］.电力电子技术，2013，47（4）：93-95.

［4］Bouafia A，Krim F，Gaubert J P.Fuzzy⁃logic⁃based Switching State Selection for Direct Power Control of Three⁃phase PWM Rectifier［J］.IEEE Transactions on Industrial Electronics，2009，56（6）：1984-1992.

［5］Cheng K W E，Wang H Y，Sutanto D.Adaptive Directive Neural Network Control for Three⁃phase AC/DC PWM Con⁃verter［J］.IEE Proceedings⁃electric Power Applications，2001，148（5）：425-430.

［6］汪万伟，尹华杰，管霖.双闭环矢量控制的电压型PWM整流器参数整定［J］.电工技术学报，2010，25（2）：67-72.

［7］张敏，刘京湘.一类参数不确定系统的鲁棒镇定［J］.控制理论与应用，2004，21（5）：830-834.

［8］张平化，杨贵杰，李铁才.三相电压型PWM整流器的反馈线性化直接电压控制［J］.中国电机工程学报，2010，30（18）：39-46.

［9］乐江源，谢运祥，张志，等.三相电压型有源电力滤波器精确反馈线性化空间矢量PWM复合控制［J］.中国电机工程学报，2010，30（15）：32-39.

Research on OptimalH∞Robust Control of the Three-phase PWM Rectifier

DU Yun⁃chao，SHAO Tian⁃zhang，GU Zhi⁃feng
（Vehicles and Electrical Department of Ordance Engineering College，Shijiazhuang 050003，Hebei，China）

Based on the disadvantages of existing classical three⁃phase PWM rectifier double⁃loop PI control strategies including current inner loop and voltage outer loop，made the improvement of current inner loop，and proposed the optimalH∞robust control based on exact feedback linearization.By analysing the dq model of three⁃phase PWM rectifier，the affine nonlinear model was built on the selected state variables and output variables.Then realized decoupled control of three phase PWM rectifier through the state feedback exact linearization，and obtained the optimal control law by the solution of Riccati inequality.The simulation results show that the proposed control method can achieve the DC output voltage to be stable and unity power factor control in a fixed range of strong disturbance and parameter perturbation.It can provide effective technical support for the emergency power supply of mobile power station.

three⁃phase PWM rectifier；exact feedback linearization；double⁃loop control；optimalH∞robust control

TM461

A

2014-12-17

修改稿日期：2015-07-07

杜运超（1992-），男，硕士研究生，Email：1203466877@qq.com