两自由度磁悬浮控制系统的稳定性与Hopf分岔分析
2015-07-07忽伟李欣业霍倩李银山
忽伟,李欣业,霍倩,李银山
(1.河北工业大学机械工程学院,天津 300130;2.河北农业大学机电工程学院,河北保定 071001)
两自由度磁悬浮控制系统的稳定性与Hopf分岔分析
忽伟1,李欣业1,霍倩2,李银山1
(1.河北工业大学机械工程学院,天津 300130;2.河北农业大学机电工程学院,河北保定 071001)
建立了基于刚性轨道的两自由度磁悬浮控制系统的非线性动力学模型,利用Hopf分岔的Hurwitz判据,推导了PD控制下平衡点稳定以及失稳产生周期振动时控制参数应满足的条件.通过数值模拟得到的磁悬浮系统产生自激振动的临界条件很好地验证了理论分析的结果.通过比较还发现间隙反馈与速度反馈相比具有更强的控制效果,这一结论为反馈控制模式的选取提供了有效的理论依据.
磁悬浮列车系统;Hurwitz判据;PD控制;Hopf分岔
0 引言
不同于传统的轮-轨车辆系统,磁悬浮系统以非接触的电磁力实现车辆的支撑和导向,因此磁悬浮控制系统是一个多体、多场耦合、强非线性的高维复杂动力学系统.有源支撑导致的振动是磁悬浮列车系统的难题之一.磁浮列车系统发生振动的原因来自多方面,如车辆结构、轨道梁结构、车辆的动态运行等.由于电磁力和悬浮间隙的平方成反比,使得磁悬浮系统本身存在固有的不稳定性.要实现稳定的悬浮,系统必须具有适当的反馈控制.
文献[1]在分析EMS列车系统结构特性的基础上,仿真分析了弹性轨道阻尼、加速度反馈增益等对静态悬浮稳定性和动态特性的影响.文献[2]提出了串级控制的思想,即控制系统由内环和外环两部分组对磁悬浮列车系统的运动稳定性进行控制.文献[3]中利用神经网络来实现PID参数的自调整与优化,达到了比较理想的控制效果.施晓红等[4-5]通过分析基于PID控制器的非线性磁悬浮系统的Hopf分岔现象,从控制参数与系统周期解稳定性角度阐述了磁浮系统产生振动的原因.洪华杰[6]从控制系统稳定性、系统的动态响应和高频激励响应讨论了在磁浮系统中用弹簧阻尼器替代控制器对系统的影响.文献[7]根据单铁模型,研究车桥耦合振动,通过改进最优控制器的参数,使控制系统在确定性输入和不确定性输入(轨面不平顺)情况下都能达到良好的性能.文献[8]对磁悬浮系统采用非线性鲁棒控制,使得系统取得了很好的鲁棒性.SinhaPK[9-10]采用模型参考自适应控制来抑制电磁悬浮的非线性影响,以磁悬浮系统的非线性模型作为可调系统,以某个线性化模型作为参考模型,并以该参考模型的状态和输出作为希望的性能指标.文献[11-12]在反馈线性化模型的基础上设计磁悬浮控制器,磁悬浮系统模型采用完全非线性化状态方程来描述,故通过反馈线性化得到的模型在很大范围内不受平衡点的影响,结果表明与在平衡点处线性化相比,直接反馈线性化方法不但简化了控制器的设计,而且可以保证控制器的全局稳定.Lin L C和Gao T B等[13]将模糊控制应用于磁悬浮控制,取得了响应速度快、超调量小,鲁棒性强的控制效果.文献[14]提出了一种基于滑模控制理论的鲁棒控制器对磁悬浮系统的位置响应进行追踪,结果表明在滑模变结构控制的作用下,磁悬浮控制系统具有很强的鲁棒性,对模型误差甚至载荷变化都有较好的适应性.此外,还出现了基因算法与神经网络在磁悬浮控制系统中应用的研究文献[15-16].周晓兵等[17]设计滑模变结构控制器并实现了磁悬浮系统的稳定悬浮,且获得了较好的控制效果.李云钢和常文森[18]对磁悬浮列车的模糊反馈控制进行了研究.刘恒坤和常文森[19]设计了实时跟踪系统参数改变的自适应控制系统,随着系统结构参数的改变相应地改变控制参数,使得系统的性能始终保持最优或者近似最优.此外,国内也有人将鲁棒控制器应用到磁悬浮控制系统[20-22].
本文基于刚性轨道、两级悬浮模型讨论反馈增益对非线性磁悬浮系统稳定性的影响,最后通过数值模拟验证理论分析的正确性.
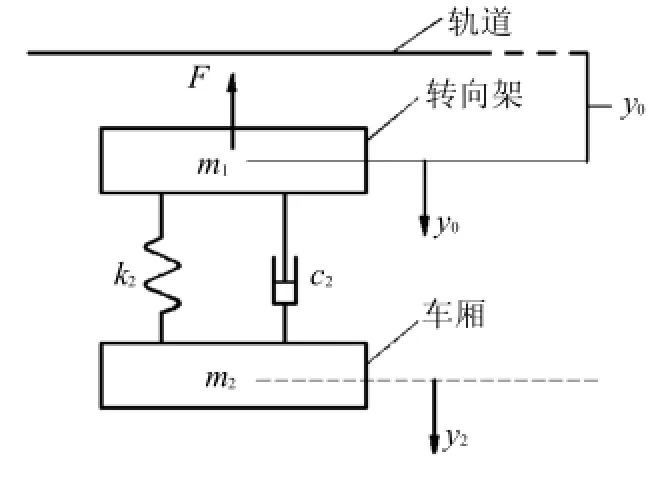
图1 悬浮控制系统模型Fig.1The schematic of maglev system
1 动力学分析模型
在图1所示的模型中,转向架构成一级悬浮体,车厢构成二级悬浮体,两级悬浮体之间由空气弹簧连接.两级悬浮体的质量分别为m1、m2;k2、c2分别表示弹簧的刚度系数和阻尼器的阻尼系数;y1、y2分别为两级悬浮体的纵向位移,y0为系统处于平衡位置时的悬浮间隙;悬浮力由电磁反馈力F提供.由于本文以悬浮控制系统为主要分析对象,所以没考虑轨道弹性变形的影响.
以m1和m2各自的平衡位置为坐标原点,正方向如图1所示.可得系统的动力学方程如下

式中:R为控制电路中的电阻;I为控制电流,它由系统平衡位置时的偏置控制电流I0和扰动电流i组成,即I=I0+i;u为控制电压,它由系统位于平衡位置时的偏置控制电压u0和变化电压uc组成,u=u0+uc,且偏置控制电流I0与偏置控制电压u0间有关系u0=I0R.电磁铁线圈中的电感为

2 Hopf分岔分析


再结合式(20),得反馈控制下平衡点稳定时,控制参数的稳定区间如图2所示(S代表稳定区域,U代表不稳定区域).
3 数值仿真
为验证以上理论分析的结果,本部分进行数值仿真时,控制参数分别取在平衡点的稳定区域、不稳定区域以及两者之间的边界上.下面给出几组kd不变,kp变化时对应的1级和2级悬浮体位移响应的时间历程和相轨迹.相图中的小红点代表初始点.kd=5,20,40时的各3组仿真结果分别如图4~图6所示.
当kp=0.243,kd分别取5、20、40即控制参数位于稳定区间的下边界时,相应的图4a)、图5a)、图6a)表明,系统在新的平衡位置稳定,没有到达所期望的控制目标,系统在原平衡位置不稳定.当kd固定kp为分岔参数时,系统在稳定区间的上边界发生了Hopf分岔,如图4b)、图5b)、图6b).当控制参数在稳定区间上取值时,系统在平衡位置渐进稳定,如图4c)、图5c)、图6c).当控制参数在不稳定区间上取值时,系统的运动是发散的,如图4d)、图5d)、图6d).根据以上数值仿真的结果,可得表1中当kd不变,系统发生Hopf分岔时所对应的临界值kp0.类似地可得当kp不变,系统发生Hopf分岔时所对应的临界值kp0.根据表1可知,当控制参数kp和kd取值相等时,所对应的临界值kd0<kp0,这表明间隙反馈比速度反馈具有更强的控制效果.
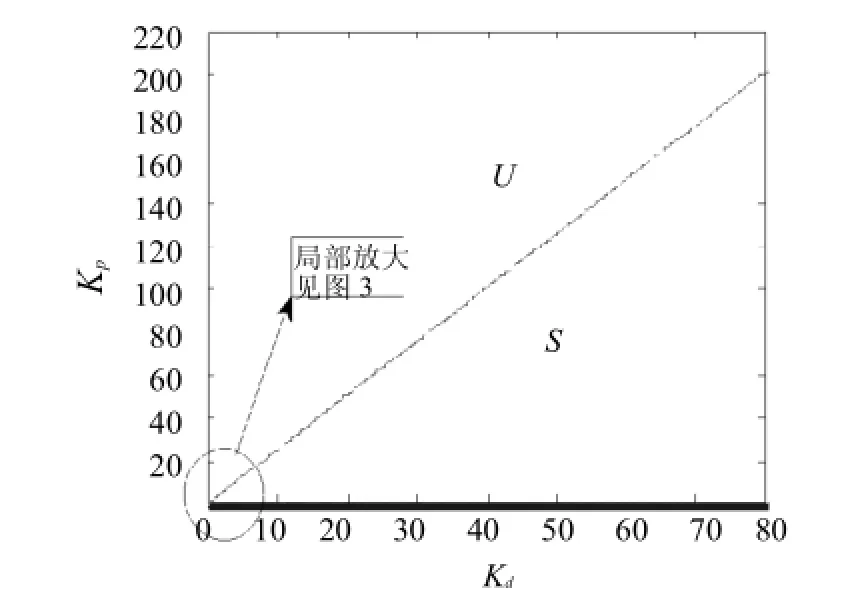
图2 平衡点的稳定边界Fig.2Stable boundaries of the equilibrium point
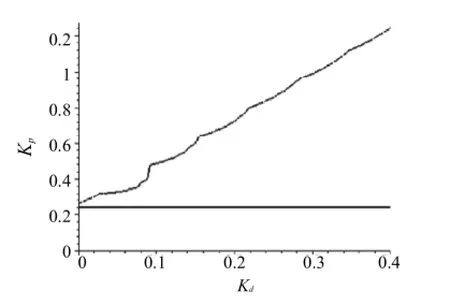
图3 图2的局部放大Fig.3The partial amplification of Fig.2

图5 kd=20时的一组时间历程和相图Fig.5A group of time histories and phase portraits when kd=20
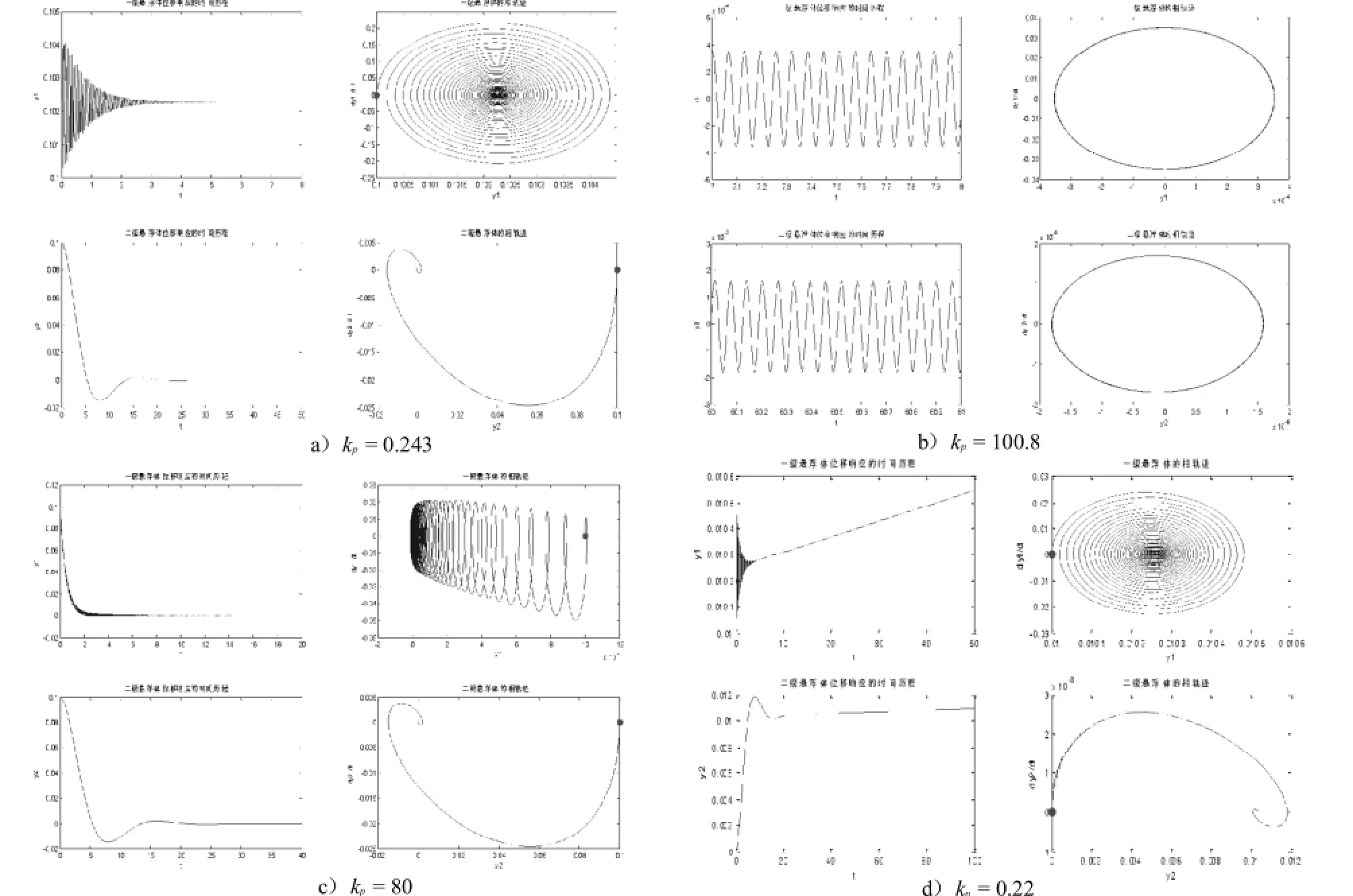
图6 kd=40时的一组时间历程和相图Fig.6A group of time histories and phase portraits when kd=40

表1 一组临界反馈增益Tab.1A set of critical feedback gains
4 结论
本文利用理论和数值方法讨论了基于PD控制和二级悬浮模型的磁悬浮系统平衡点的稳定性以及发生Hopf分岔的条件,所得结论如下
1)利用Hopf分岔的Hurwitz判据给出了在反馈增益kp-kd平面内平衡点的稳定区间以及发生Hopf分岔和鞍-节分岔的边界.
2)数值计算发现磁悬浮系统的失稳有3种形式即产生Hopf周期解、到达新的平衡位置和发散.
3)当控制参数kd和kp的取值相等时,系统出现Hopf分岔而产生周期振动所对应的临界值kd0<kp0,这说明间隙反馈比速度反馈具有更强的控制效果.
4)数值解很好地验证了基于Hurwitz判据所作的理论预测.
[1]谢云德,常文森.电磁型(EMS)磁悬浮列车系统铅垂方向的建模与仿真[J].铁道学报,1996,18(4):47-54.
[2]李云钢,常文森.磁浮列车悬浮系统的串级控制[J].自动化学报,1999,25(2):247-251.
[3]Sinha P K,Hadjiiski L M,Zhou F B,et al.Electromagnetic suspention:new results using neutral network.IEEE Transaction on Magnetics[J].1993,29(6):2971-2973.
[4]施晓红,佘龙华.非线性磁悬浮控制系统的周期运动稳定性研究[J].动力学与控制学报,2005,3(3):52-55.
[5]施晓红,佘龙华,常文森.EMS磁浮列车车轨耦合系统的分岔现象研究[J].力学学报,2004,36(5):634-640.
[6]洪华杰,李杰.磁浮系统模型中用弹簧阻尼替代控制器的等效性分析[J].国防科技大学学报,2005,27(4):101-105.
[7]Macleod C,Goodall R M.Frequency shaping LQ control of maglev suspention system for optimal performance with deterministic and stochastic inputs[J].IEEE Proceedings of control theory applications,1996,143(1):25-30.
[8]Kaloust J,HamC,SieghlingJ,et al.Nonlinear robustcontrol designforlevitationandpropulsionofmaglevsystem[J].IEEE,2004,151(4):460-461.
[9]Sinha P K.Electromagnetic suspension dynamic and control[M].Peter Peregrinus,1987.
[10]SinhaPK,PeehevAN.Modereferenceadaptivecontrol ofamaglevsystemwithmaximumdesent criterion[J].Automatica,1999,35(8):1475-1465.
[11]YangZ J,MinashimaM.Robustnonlinearcontrol ofafeedbacklinearizablevoltage-controlledmagneticlevitationsystem[J].TransIEEE Japan,2011,121(7):1203-1211.
[12]刘恒坤,常文森.磁悬浮系统的两种线性化控制方法[J].自动化技术与应用,2005,24(1):14-17.
[13]LinL C,GaoTB.Feedbacklinearizationandfuzzycontrol ofcontrolofconventionalmagneticbearing[J].IEEETransControlSystemTechnology,1997,(5):913-920.
[14]MahdiJalili-Kharaajoo,ManimesgarpourTousi,HassanBaghezadch,et al.Slidingmodecontrol ofvoltage-controlledmagneticlevitationsystems [J].IEEE,2003:83-86.
[15]Schroder P,Green B,Grum N,et al.Online genetic auto-tuning of mixed H2/H∞optimal magnetic bearing controllers[J].IEE Conference Publication,1998,455(2):1123-1128.
[16]许洁,刘春生.基于神经网络的磁悬浮球自适应控制器[J].机电工程,2007,24(3):22-24.
[17]周晓兵,龙志强,李云钢,等.磁悬浮列车滑模控制变结构控制器设计及实现[J].国防科技大学学报,1997,19(4):87-93.
[18]李云钢,常文森.磁浮列车的模糊反馈控制[J].模糊系统与数学,1998,12(1):54-59.
[19]刘恒坤,常文森.磁悬浮系统的简单自适应控制[J].电光与控制,2005,12(2):68-73.
[20]范素香,段吉安.鲁棒控制理论在磁悬浮球系统中的应用[J].现代机械,2005(4):1-2.
[21]刘峰,龙志强,尹力明.磁悬浮列车系统的鲁棒控制分析[J].机车电传动,1996(5):23-26.
[22]孙玉坤,张昆仑.磁悬浮列车的非线性鲁棒控制.机车电传动[J],2005(6):26-28.
[23]吴海超,方海容.基于Huriwitz判据的悬浮控制系统稳定性分析[J].铁道学报,2012,34(12):41-45.
[24]武建军,沈飞,史筱红.磁悬浮控制系统的稳定性及Hopf分岔的研究[J].振动与冲击,2010,29(3):194-196.
[25]沈飞.磁悬浮控制系统的动力稳定性研究[D].兰州:兰州大学,2009.
[26]王浩,邹东升,佘龙华.利用Hurwitz代数判据研究磁悬浮系统Hopf分岔现象[J].电力机车与城轨车辆,2009,32(1):21-24.
[责任编辑 田丰夏红梅]
Stability and Hopf bifurcation of maglev vehicles with two degrees of freedom
HU Wei1,LI Xinye1,HUO Qian2,LI Yinshan1
(1.School of Mechanical Engineering,Hebei UniversityofTechnology,Tianjin300130,China;2.CollegeofMechanicalandElectrical Engineering,Agricultural University of Hebei,Hebei Baoding 071001,China)
Based on the rigid guideways,the nonlinear dynamic model of maglev vehicles with two suspensions is presented.By the Hurwitz criterion,the domain where the equilibrium is stable under PD control is deduced and illustrated in the plane of the control parameters.The two boundaries of the stable domain of the equilibrium are corresponding to the conditions of Hopf and saddle-node bifurcations.According to the numerical simulations which are consistent with theoretical analysis,it is found that the response may be divergent corresponding to parameter domain where the equilibrium is unstable,periodic corresponding to the boundary where Hopf bifurcation occurs,or a new equilibrium corresponding to the boundary where saddle-node bifurcation occurs.By comparison,it is shown that displacement feedback has better and stronger control performance than velocity feedback.
maglev vehicles;hurwitz criterion;PD control;hopf bifurcation
TG501
A
1007-2373(2015)05-0038-07
10.14081/j.cnki.hgdxb.2015.05.008
2014-12-02
河北省高层次人才资助项目(C201400309);国家自然科学基金(10872063)
忽伟(1989-),男(汉族),硕士生.通讯作者:李欣业(1966-),男(汉族),教授,博士生导师.
数字出版日期:2015-10-19数字出版网址:http://www.cnki.net/kcms/detail/13.1208.T.20151019.0953.002.html
