固定通信台站装备保障人员需求预测研究

栗志荣， 高 崎， 刘慎洋， 陈为元

(1.太原卫星发射中心，山西 岢岚 036301; 2.军械工程学院 装备指挥与管理系，河北 石家庄 050003)



固定通信台站装备保障人员需求预测研究

栗志荣1,2， 高 崎2， 刘慎洋2， 陈为元2

(1.太原卫星发射中心，山西 岢岚 036301; 2.军械工程学院 装备指挥与管理系，河北 石家庄 050003)

固定通信台站维修保障人员是装备保障的主体。将固定通信台站保障任务分为通信值勤、预防性维修保障及修复性维修保障任务三类，分析三类保障任务特点，确定保障人员需求预测方法。分析值勤人员动态特点，计算值勤人员需求期望向量；分析预防性维修任务量和维修时间，建立预防性维修人员需求量的周期模型；通过积分法分析修复性保障任务的任务量，估计修复性维修人员的需求量。

人力资源管理； 人员需求预测； 任务量分析； 通信值勤； 预防性维修； 修复性维修

0 引言

固定通信台站是根据军事任务、作战部署和指挥要求，由固定的通信设施和相应的机构、人员组成的通信组织整体[1]。保障人员作为装备保障的主体，是保障过程的执行者，直接影响着台站装备保障效能的发挥。维修保障人员数量过多，会造成冗余浪费；人员数量过少，则难以满足维修保障的需求。因此，研究如何做好保障人员需求预测，为台站分配数量合理的保障人员，是当前需要解决的重要问题。

目前，在装备保障人员预测方面存在许多方法，例如灰色预测法[2]、排队论方法[3]、基于工作量分配的方法[4]等，在考虑人员动态时，保障人员预测及配置方面的研究还主要有：刘广宇将马尔科夫和灰色理论相结合，对部队装备技术保障人员预测进行了相关的研究[5]；Guerry在人力资源不均衡性的前提下，建立了马尔科夫状态转移模型[6]；Khan和Chattopadhyay在人员与岗位需求匹配的基础上建立了相应的人员流动预测函数[7]；饶建伟、胡伟文运用动态规划模型对基层部队人力资源进行优化配置[8]。本文在现有研究成果的基础上，结合固定通信台站装备保障特点，进行保障人员需求预测研究。

1 保障人员需求预测分析

图1 固定通信台站装备保障任务结构图

固定通信台站装备保障人员需求数量与装备保障任务量直接相关。固定通信台站装备保障需要完成的任务可分为三类：通信值勤、预防性维修和修复性维修，其中预防性维修与修复性维修又可统称为维修保障(如图1所示)，它们是进行维修管理决策的重要依据。考虑到固定通信台站实际，各岗位所属装备类型、型号、使用时间的不同，造成装备(部件)的维修保障数量不能体现所有保障活动特点，因此本文使用装备保障活动次数来反映任务量，最终通过任务量来反映并预计保障人员数量。其中，保障活动次数体现在通信值勤中为装备操作使用及维护次数、体现在预防性或修复性维修保障活动中为维修活动实施次数。

通信值勤是人员为确保通信联络迅速、准确、保密、不间断，依据一定的标准和规则，对台站及运行中的通信装备所进行的操作、使用、维护等管理活动[9]，是通信台站的中心工作。根据条令条例及规章制度的要求，固定通信台站各岗位需要配备通信值勤人员，实施不间断的通信值勤。各岗位依据实际情况确定值勤时间段，并合理安排人员完成值勤期间的各项保障活动。假设固定通信台站岗位数为l，由于值勤常态化，第i(i=1,2,…,l)岗位平均每天值勤任务量SZi变化幅度较小，通信值勤人员需求量可表示为值勤任务量的函数：

(1)

其中，NZ表示通信值勤人员需求量；NZi表示第i岗位值勤人员需求量，i=1,2,…l。

图2 保障任务量变化示意图

预防性维修和修复性维修一般统称为维修保障活动，即维修保障人员利用一定的手段来维持或恢复通信设备和设施的性能，以保证其正常运行的活动[10]。固定通信台站各岗位装备预防性维修具有周期规律，依据预防性维修任务量SWYi(t)的周期特点(如图2所示)，人员需求NWY(t)也具有周期性；修复性维修所针对的保障任务种类较多，部分简单故障由修复性维修人员修复时所需人员数量较少，在维修任务量SWXi(t)增大时，保障人员需求量也随之增加，所以参与修复性维修保障活动的人员需求量为一个动态变量:

(2)

其中，NWX(t)表示固定通信台站修复性维修人员需求量；NWXi(t)表示第i岗位修复性维修人员需求量，i=1,2,…l。

假设固定通信台站所有保障人员均可完成通信值勤和维修保障任务，由图2可知，在某个时刻t，依据任务量来确定的装备保障人员需求量可表示为:

N(t)=max[NZ,NWY(t),NWX(t)]

(3)

其中，NZ、NWY(t)、NWX(t)分别表示值勤人员、预防性维修人员和修复性维修人员需求量。

2 保障人员需求预测模型

2.1 通信值勤活动人员需求预测模型

机关决策者决定固定通信台站参与通信值勤活动的保障人员的多少，主要是基于不同岗位任务量的考虑，可以简单认为是一种线性关系。即：

NZi=f(SZi)=β1β2…βaSZi

(4)

其中，wi(t)为第i岗位在一个时间段[t-1,t)内人员退出的概率，人员退出包括人员非自然退出和值勤期满自然轮换。由于值勤人员的退出，在时刻t会有一定的人员空缺。定义向量V(t)=[v1(t)，v2(t)，…，vl(t)〗，vi(t)表示第i岗位在一个时间段[t-1,t)内值勤人员的空缺数量，空缺数量(向量)可由下式方法计算：

(5)

如果出现人员空缺，可通过岗位调整，将数量较多的岗位人员进行调整来补充空缺。定义概率矩阵:

其中pij(t)表示从岗位j补充到岗位i的概率，其前提是不能造成岗位j的人员空缺。一般情况下，岗位间调整无法满足岗位空缺量，因此需要额外调入人员来参与通信值勤任务。假设，R(t)表示时刻t补充至台站的值勤人员的数量；向量r(t)=[r1(t)，r2(t)，…，rl(t)]表示时刻t人员补充至各岗位的比例，则：

R(t)r(t)=V(t)-N*(t)P(t)

(6)

结合式(5)及式(6)，时刻t各岗位可满足需求的值勤人员数量的期望向量为：

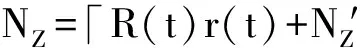
(7)

其中，符号“「⎤”表示向上取整。

2.2 预防性维修保障活动人员需求预测模型

预防性维修是在故障发生之前采取维护行动的维护方式，具有周期性的特点，固定通信台站预防性维修有多个阶段，如周、月、季度、年等。本节通过预防性维修任务量确定总时间，并结合单个保障人员平均工时来计算所需保障人员数量。

(1)维修任务量计算

预防性维修的任务量由预防性维修保障活动次数来反映。假设预防性维修活动的阶段表示为j(j=1，2，3，4分别表示周、月、季度和年)，易知，第j阶段预防性维修保障活动发生次数SWYj与通信装备运行时间和此阶段保障活动周期有关。

第i岗位装备在第j阶段预防性维修保障活动下的运行时间Tij计算公式为：

Tij=TRijniηWiqi

(8)

其中，TRij——第i岗位单装在第j阶段预防性维修保障活动下的运行时间=工作天数×每天工作小时数；ni——第i岗位装备数量；ηWi——第i岗位装备运行比例；qi——第i岗位装备运行强度系数，表示某装备一天中开机运行的次数。

由于第j阶段预防性维修周期包含了低一阶段的预防性维修周期，因此，第j阶段预防性维修周期以该阶段最小周期记。于是可以得出第j阶段预防性维修活动次数[12]的计算公式为：

(9)

其中：TWYij——第i岗位装备在第j阶段中预防性维修的周期。

(2)保障人员数量预测

预防性维修保障活动人员数量由维修总时间和单个保障人员平均工作时间共同决定。

首先，需要确定预防性维修保障活动总时间。为了建立一个准确的时间函数，可以从修理方式出发：固定通信台站预防性维修方式包括停机修理和不停机修理，假设X=(x1,x2,…,xj,…,xn)为n阶段预防性维修的停机修理比率，表示为：

(10)

其中，Shj为第j阶段预防性维修活动停机修理次数。易知，xj=1表示全部采取停机修理，xj=0则表示全部不停机修理。所以，固定通信台站装备第j阶段预防性维修总时间可表示为停机修理比率xj的函数TWY(xj)，即：

(11)

其中，Tj1、Tj2为第j阶段预防性维修的停机修理时间和不停机修理时间；pi为第i岗位参加预防性维修的装备比率。

固定通信台站预防性维修活动中，首要目标是精简维修方式，减少停机时间，使得对通信装备运行影响最小。因此，我们需要针对停机修理时间进行优化，最优化模型为：

(12)

第j阶段预防性维修活动中，单个保障人员平均工作时间可以依据下式计算：

(13)

其中，Thj表示单人每次在第j阶段预防性维修活动中有效工作时间；γ为出勤率。

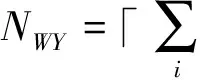
(14)

[例] 某固定通信台站有专业岗位6类，假设各岗位装备从某时刻开始运行，在时刻T正好经历50天。各岗位装备运行基本数据如表1所示。

表1 各岗位装备运行基本数据表

假设各岗位装备预防性维修周期相同，那么截止时刻T最小预防性维修阶段为j=1，即维修周期长为7×24=168h，依据式(9)可计算出各岗位预防性维修次数，如表2所示。然后统计各岗位装备每次停机和不停机维护的时间，依据式(11)得出预防性维修时间，表示为停机修理次数的函数。如果假设每岗位装备每停机修理一次消耗备件量为1，不停机修理不消耗，且备件限量为装备数量，那么结合式(12)可求解出各岗位装备预防性维修时间。依据式(13)计算人员平均工时并代入式(14)最终可得人员需求量结果如表2所示。

表2 预防性维修活动分析数据表

可知，在时刻T，固定台站各岗位预防性维修人员需求量为NWY=[3,2,2,1,2,1]，结果基本符合实际情况。

另外，由于预防性维修保障活动任务量具有周期性(如图2)，如果第j阶段预防性维修保障活动第一次开始时间为T0，则其周期性可表示为函数：

(15)

所以，结合式(14)及式(15)，可以将第j阶段预防性维修保障活动所需求人员NWY(t)表示为一个阶段时间函数：

NWY(t)=NWYy(t)

(16)

2.3 修复性维修保障活动人员需求预测模型

修复性维修是及时恢复装备良好技术状态的主要措施，是装备技术保障的核心任务。通过通信值勤人员的装备保养和定期的预防性维修，修复性维修任务量会有一定程度上的降低，但是，由于人员失误的存在和装备故障增加的不可逆性，修复性维修任务量在长期看来是一直存在的，因此本节对修复性维修任务量的研究不考虑装备保养和预防性维修的影响。固定通信台站各岗位所属装备在平时使用过程中，决定装备修复性维修任务量的主要因素有：装备故障率、装备运行时间以及装备运行数量等。如果可以确定第i岗位装备的故障次数，那么固定通信台站装备修复性维修次数就可以确定。

图3 装备故障率示意图

本文不讨论固定通信台站装备故障率特点，我们在此处假设装备故障率为一随时间增加而增加的函数λik(t)，表示第i岗位的第k装备的故障率。如图3。

假设装备运行的一个起止时间段为[T1,T2]，由于部分装备运行的不连续性，我们将该时间段分为n个区间：[t0,t1]，(t1,t2]，…，(tn-1,tn]，其中，t0=T1,tn=T2，各时间段均匀且足够小，使得装备在各时间段内为连续运行。假设第i岗位的第k装备在各时间段运行时间分别为Δtk1，Δtk2，…，Δtkn，在每个时间区间取一点tkj，可将第i岗位的第k装备在各时间段的故障率表示为λikj(t)。那么由于各时间段足够小，可以近似认为在[T1,T2]内第i岗位第k装备故障次数为：

(17)

依据定积分概念，如果定义α=max{Δtk1，Δtk2，…，Δtkn}，那么在时间段[T1,T2]内，第i岗位第k装备故障发生总次数为下式所示：

(18)

我们在考虑装备故障次数时，不仅仅需要有式(18)计算的装备自身故障次数，在维修保障活动中由于人员操作失误造成的装备故障(下称人为故障)次数也需要包括在内。人为故障次数可由下式计算：

(19)

其中，Drki——第i岗位第k装备人为故障次数；Mki——第i岗位第k装备需执行的保障任务数；μwki——第i岗位第k装备人员在执行保障任务w时的失误率，主要是为了区分由于保障任务的难度差异造成的人为故障概率的不同；pwki——第i岗位第k装备执行保障任务w的频数比。

修复性维修在装备故障后进行，那么固定通信台站装备修复性维修次数可以依据下式确定：

(20)

其中，ni表示第i岗位装备数量；Dki(t)表示第i岗位第k装备故障发生次数，依据式(18)可表示为Dki(t)=∫λik(t)dtk

由于固定通信台站涉及的维修属于基层级维修，因此需要先考虑故障是否可进行现场修复，再决定人员需求量。①如果可现场修复，需要考虑人员平均技术水平、修复率等因素进而计算平均修理时间Tx；②如果不能现场修复，则修复性维修只包括换件操作，需要统计换件修理的平均时间Ty。显然，两种情况不会同时发生，那么综合考虑下，单次修复时间为Tm=max(Tx,Ty)。所以，固定通信台站装备修复性维修人员需求量可按下式计算[14]：

(21)

其中TN表示单个保障人员单次维修活动的最大工作时数；ε表示修理停工率。

于是，将式(7)、式(16)和式(21)代入式(3)可以最终确定固定通信台站装备保障人员需求量。

3 总结

本文将保障任务分为通信值勤、预防性维修保障及修复性维修保障任务三类，通过分析固定通信台站三类保障任务的特点，确定保障人员需求预测方法。利用动态特点，计算并优化值勤人员需求量；通过分析预防性维修任务量和优化维修时间，建立预防性维修人员需求量的周期模型；通过分析修复性保障任务的任务量，估计修复性维修人员的需求量。需要说明的是，在预测出固定通信台站所需装备保障人员数量之后，还应将分析结果与固定通信台站实际编制及各岗位容量进行对比，做出相应的调整，并通过装备保障过程中的人员使用情况加以修正。

[1] 黄廷忠.军以下部队固定通信组织与管理[M].武汉：通信指挥学院,1997.

[2] 宋雪静.基于灰色理论的船舶工程技术人才需求分析[J].山东轻工业学院学报, 2007,2(29):116-120.

[3] 杨光辉，宋建社，屈晓荣.基于排队论的装备维修人员数量需求模型[J].指挥控制与仿真,2007,29(2):116-120.

[4] 耿斌.复杂武器装备的维修人力需求预测研究[D].军械工程学院硕士学位论文,2006.

[5] 刘广宇.装备技术保障人力资源的优化配置研究[D].军械工程学院硕士学位论文,2002.

[6] Marie-Anne Guerry. Hidden heterogeneity in manpower systems: a markov-switching model approach[J]. European Journal of Operational Research, 2011, (210): 106-113.

[7] Khan S, Chattopadhyay A K. Predictive analysis of occupational mobility based on number of job offers[J]. Journal of Applied Statistical Science, 2003, 12(1): 11-22.

[8] 饶建伟，胡伟文.基层部队人力资源优化配置的动态规划模型研究[J].运筹与管理,2009,18(5):116-120.

[9] 翟拴领.固定通信台站值勤与训练[M].西安：西安通信学院.2007.

[10] 刘建国，毕进南.通信装备保障概论[M].北京：军事科学出版社,2006.

[11] Marie-Anne Guerry, Tim De Feyter. An extended and tractable approach on the convergence problem of the mixed push-pull manpower model[J]. Applied Mathematics and Computation, 2011, (217): 9062-9071.

[12] 邱燕琳，王治宇，章文晋.基于保障活动流程的装备保障使用与维修人力资源需求预测模型[J].装备指挥技术学院学报，2011,22(6):61- 66．

[13] 周赤非.新编军事运筹学[M].北京：军事科学出版社,2010.

[14] 郝杰忠，杨建军，杨若鹏.装备技术保障运筹分析[M].北京：国防工业出版社,2006.

Research on Forecasting Equipment Support Personnel Requirement in Immobile Communication Station

LI Zhi-rong1,2, GAO Qi2, LIU Shen-yang2, CHEN Wei-yuan2

(1.TaiyuanSatelliteLaunchCenter,Kelan036301,China; 2.DepartmentofEquipmentCommandandManagement,OrdnanceEngineeringCollege,Shijiazhuang050003,China)

The materiel support personnel of immobile communication station are the key to equipment support. Working quantity in an immobile communication station can be divided into three categories: the communication duty, preventive maintenance, and corrective maintenance. Making use of the dynamic factor, requirement of communication duty personnel is calculated and optimized; preventive maintenance personnel requirement model is established based on the analysis of the task size and working time; and the number of corrective maintenance personnel is estimated, through analyzing of peculiarity of the task size by integral method.

human resource management; personnel requirement forecast; task size analysis; communication duty; preventive maintenance; corrective maintenance

2013- 04- 01

栗志荣(1985-)，男，硕士研究生，主要研究方向：装备保障理论与应用。

C939,E92

A

1007-3221(2015)01- 0179- 06