三维欧氏Steiner最小树的Delaunay四面体网格混合智能算法

王家桢， 马 良， 张惠珍

(上海理工大学 管理学院，上海 200093)



三维欧氏Steiner最小树的Delaunay四面体网格混合智能算法

王家桢， 马 良， 张惠珍

(上海理工大学 管理学院，上海 200093)

Steiner最小树问题是组合优化中经典的NP难题，在许多实际问题中有着广泛的应用，而三维欧氏Steiner最小树问题是对二维欧氏Steiner最小树问题的推广。由于三维欧氏Steiner树问题的求解非常困难，至今为止的相关成果较为少见。本文针对该问题，利用Delaunay四面体网格剖分技术，提出了一种混合型智能求解方法，不仅可以尽量避免拓扑结构陷入局部最优，且对较大规模的问题求解亦有良好的效果。算法在Matlab环境下编程实现，经实例测试，获得了满意的效果。

三维欧氏Steiner最小树；Delaunay四面体网格；凸多面体剖分；智能算法

0 引言

Steiner树问题是指连接给定点的最小树长问题，其最优解称为Steiner最小树(Steiner Minimum Tree，SMT)[1]。根据点和连线的空间属性，Steiner树问题可进一步细分为欧氏Steiner树(Euclidean Steiner Tree，EST)问题和绝对值距离Steiner树(Rectilinear Steiner Tree，RST)问题(连线只有水平和垂直两种形式)。

三维欧氏Steiner树问题是对二维欧氏Steiner树问题的推广，其计算的复杂性和求解的难度超过了二维欧氏Steiner树问题[2]。国内外对此问题的相关研究成果也较少，以致对该问题的求解方法极为欠缺。

本文基于计算几何中Delaunay四面体网格的相关理论，利用智能算法，设计了一种混合型智能求解方法，其特点在于从几何的角度入手，同时结合了智能算法的特点，为该问题的实际求解提供了有效方法。

1 欧氏Steiner最小树问题

1.1 定义

给定原点集X(也称正则点集)，欧氏Steiner树是指连接点集X中所有点的最短树。由于允许增加辅助点集S(s-点集)，因此，欧氏Steiner最小树问题的本质就是寻求点集S，使得连接X∪S的生成树最小。

1.2 性质

对于欧氏Steiner最小树问题，若能设法求出s-点的数目与位置，就可用最小生成树算法对其进行求解，因此，问题的关键在于 s-点的选取。

下面，先列出几条关于二维欧氏Steiner最小树的基本性质[1]：

性质1 SMT上任何两条邻接边的夹角不小于120度。

性质2 SMT上任何一个顶点的关联边不多于三条。

性质3 SMT上与s-点相关联的边必定为三条，且这三条边中任意两边夹角为120度。

性质4 设SMT的原点为n个，则s-点的数目≤n-2。

性质5 假设由n个原点所围成的区域为凸壳，则所有s-点都必定包含在凸壳内。

性质6 SMT中每个叶子都是原点。

在文献[2]和[3]中已说明，上述6条性质可推广到三维欧氏Steiner最小树。

1.3 拓扑结构

令X={A1,…,An}为n个原点所成之集。令G为一将此n个点连接起来的最小网络，若过G上的每个s-点皆有三条边通过，它们两两交成120度的角，且任何两条边不相交，又若过其中每个原点只有一条边通过，则称G具有满拓扑[1]。

下面的所有讨论都假定欧氏Steiner最小树是满拓扑的。

(1)二维的情况

当n=3,4,5时，有关的Steiner树只出现一种满拓扑结构,如图1所示。

当n≥6时，则不止一种。

例如，对于n=6时，则有如图2所示的三种满拓扑结构。

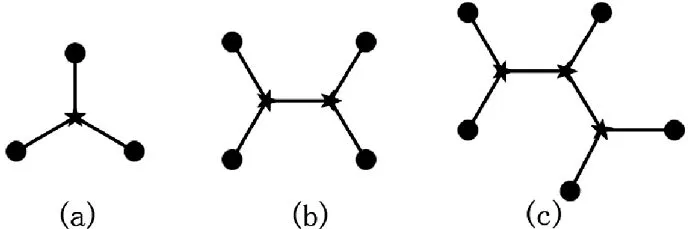
图1 二维欧氏Steiner树的满拓扑结构示意(1)

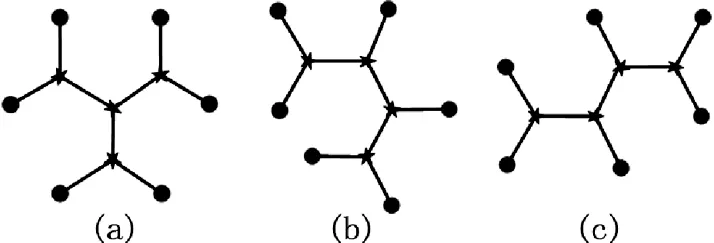
图2 二维欧氏Steiner树的满拓扑结构示意(2)

(2)三维的情况

当n=4,5时，有关的Steiner树同二维的情况一样，只出现一种满拓扑结构。值得注意的现象是，三维的情况相对于二维的情况来说，只是在空间上以一个s-点和另一个s-点的连线作为轴，将两侧的分支进行了旋转。如：图1(b)对应图3(a)，图1(c)对应图3(b)。

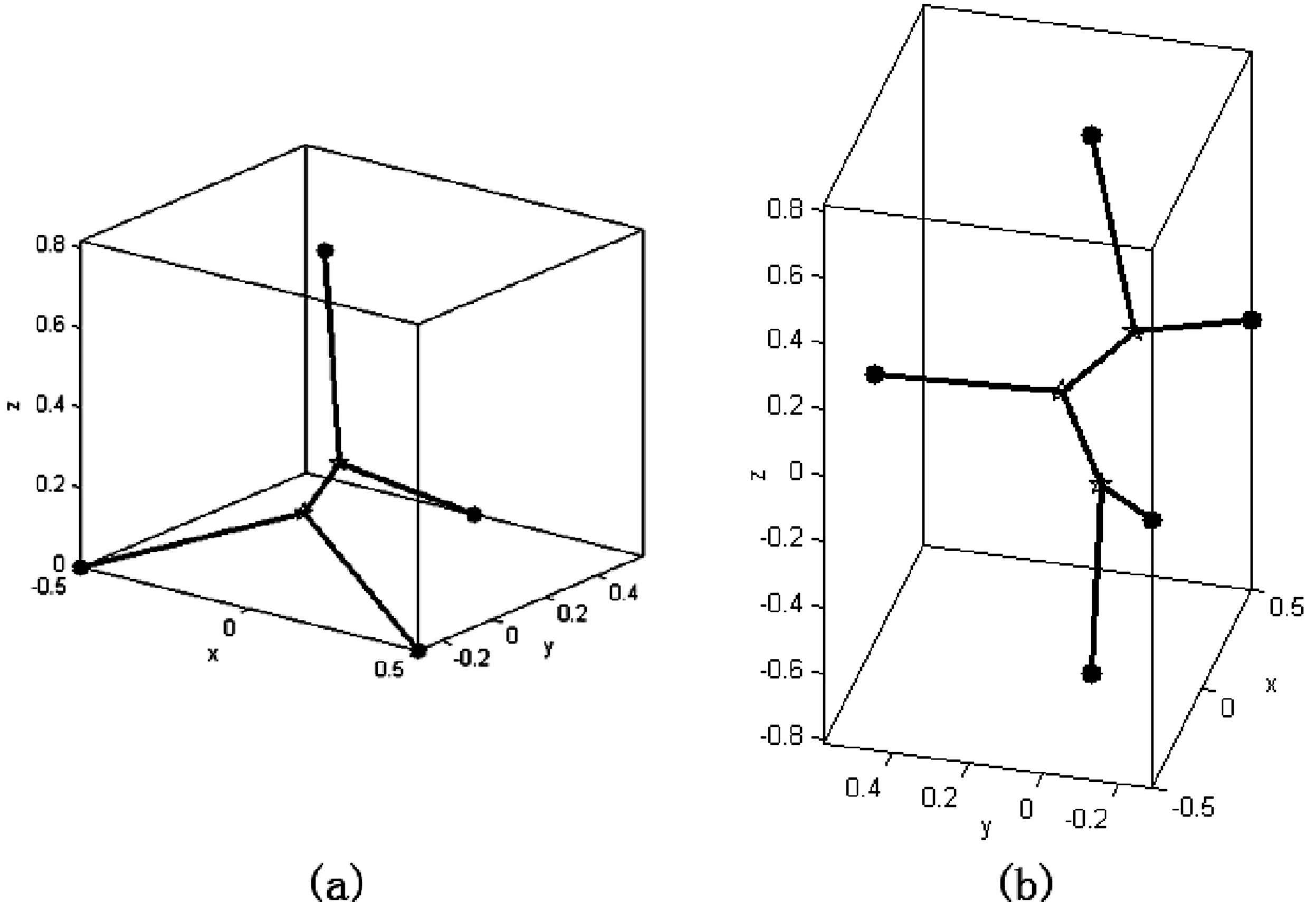
图3 三维欧氏Steiner树的满拓扑结构示意(1)

当n=6时，三维的情况则有所不同。图4中的3张图看似是对图2中二维的3种拓扑结构的推广，但是实际上图4中(b)和(c)这两张图是同一个三维图像的不同观察角度，因此三维拓扑结构的分类变成了一件棘手的事情。

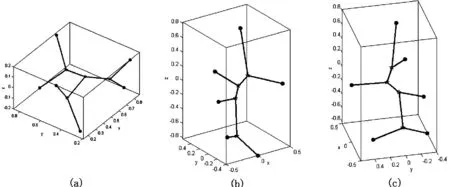
图4 三维欧氏Steiner树的满拓扑结构示意(2)

本文中将用s-点之间的连接方式来对不同的三维满拓扑结构进行归类。

当s-点的个数为2和3时，显然只有一种连接方式。

当s-点的个数为4时，有两种连接方式。图4(a)对应图5(b)，图4(b)(c)都对应图5(a)。

同理，当s-点的个数为5时，有三种连接方式，如图6。

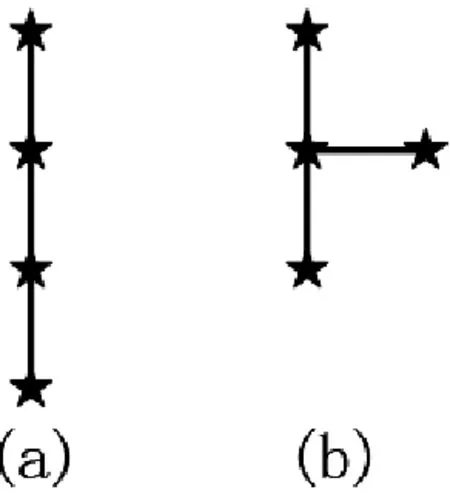
图5 三维欧氏Steiner树的满拓扑结构示意(3)

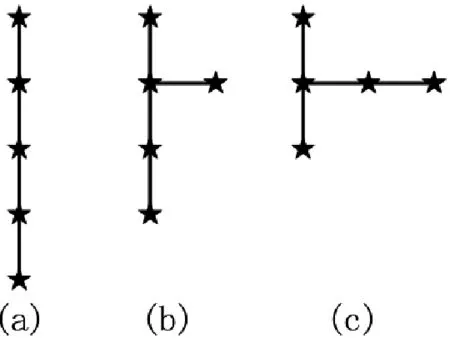
图6 三维欧氏Steiner树的满拓扑结构示意(4)

当s-点的个数为6时，有五种连接方式，如图7。

当s-点的个数为7时，有九种连接方式，如图8。

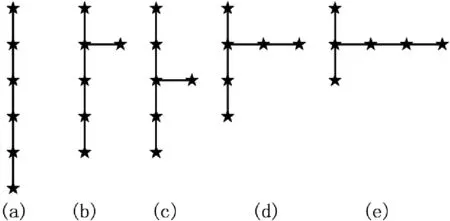
图7 三维欧氏Steiner树的满拓扑结构示意(5)

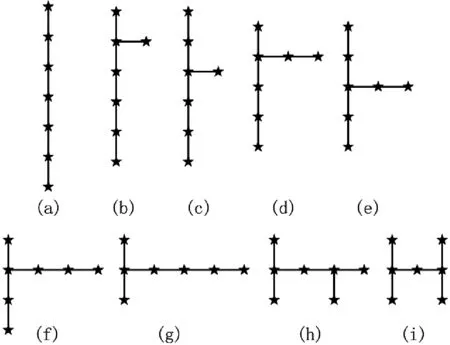
图8 三维欧氏Steiner树的满拓扑结构示意(6)

显然，按照如上的归类方法，连接方式的种数随着s-点的个数增加而增加。

在文献[3]中，讨论了关于3-Sausage结构(即图5、6、7、8中(a)的结构)的三维欧氏Steiner最小树的一些性质，该文献指出，即使已知是3-Sausage结构的Steiner最小树，也只能求得正则点数在15个点以内的精确解。

而在文献[1]中，讨论了二维欧氏Steiner最小树的正则点个数n和二维中相应归类方法得到的归类数目，当n=6时，其归类数为5625，当n=8时则为2643795。如此庞大的数目只能依靠高速计算机来处理。当n稍大，例如大于10时，问题已不可能用枚举法来求解。

又文献[2]中提到，三维欧氏Steiner最小树问题显然比二维欧氏Steiner最小树问题来得更为复杂。

因此，综合以上几点，对于空间任意点要想求解其三维欧氏Steiner最小树，如果不知道其确切的拓扑结构，即使规模很小(在10以内)，都几乎难以使用精确算法进行求解，所以，本文将介绍一种新型的混合智能求解算法来求解较大规模的该问题。

2 空间点集Delaunay四面体网格的基本概念[4,5]

(1)Delaunay规则:空间四面体外接球面的内部不包含空间点集中的点作为四面体生成的一个约束条件, 称之为Delaunay规则。在平面上，相应的约束条件为三角形的外接圆的内部不包含点集中的点。

(2)Delaunay三角形:符合Delaunay规则的三角形称为Delaunay三角形。

(3)最大空圆凸多边形:以某个Delaunay三角形的外接圆上的所有点集中的点为顶点构成的凸多边形称为最大空圆凸多边形。

(4)Delaunay 四面体:符合Delaunay规则的四面体称为Delaunay四面体。

(5)最大空球凸多面体:以某个Delaunay四面体的外接球面上的所有点集中的点为顶点构成的凸多面体称为最大空球凸多面体。

(6)凸壳:包含平面上一个点集在其所围闭区域内的最小凸多边形称为这个平面点集的凸壳。包含空间一个点集在其所围闭区域内的最小凸多面体称为这个空间点集的凸壳。

3 算法描述及示例

第一步 对给定的正则点集构建Delaunay四面体网格。具体算法此处不赘述，操作相对简单，只需在Matlab中调用函数Delaunay3即可。

第二步 对第一步中所形成的凸多面体进行剖分。剖分遵循如下规则：

(1)剖分必须沿着Delaunay四面体网格中四面体的面；

(2)找出每个四面体面积最大的面，如果该最大面为两个四面体的公共面，则将两个四面体拼接在一起。

图9 Delaunay四面体网格示意(1)

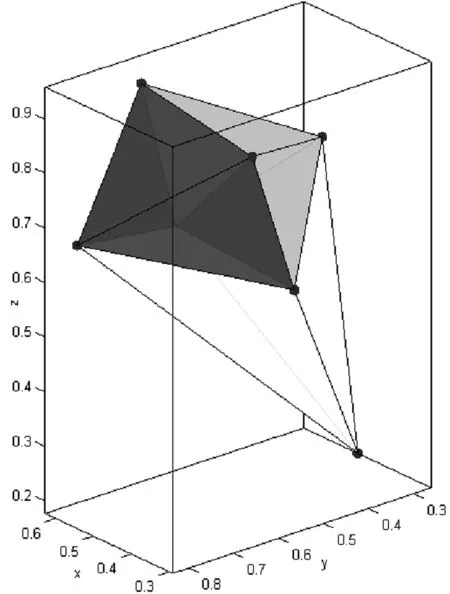
图10 Delaunay四面体网格示意(2)

第三步 利用智能算法对剖分后每一块区域的正则点进行Steiner点求解。

本环节所用智能算法的核心为遗传算法，其基本原理是借鉴自生物进化思想的随机优化算法，通过选择、交叉、变异等操作产生下一代的解，并逐步淘汰掉适应度值较低的解，获得适应度值较高的解，经过多次这样的操作得出适应度最高的解。

(1)染色体的产生。本文求解三维欧氏Steiner最小树的遗传算法中，染色体的产生尤为关键。

在1.2节中对于欧氏Steiner最小树的性质有这样的描述：假设由n个原点所围成的区域为凸壳，则所有s-点都必定包含在凸壳内。对于三维欧氏Steiner最小树来说，凸壳即为包含所有原点的最小凸多面体。

要想在凸多面体中生成一个随机点，这是一个棘手的问题。本文利用了Delaunay四面体网格的剖分算法，对原点进行了四面体网格剖分，且剖分后的四面体的集合刚好是原点的凸多面体。

经上述剖分处理后，产生染色体的方法为设置染色体的长度为(n-2)×3，每3个数代表一个s-点的x、y、z坐标。随机选择一个四面体，在该四面体中均匀分布的产生一个随机点，如此循环生成n-2个随机点，即生成一条染色体。

(2)染色体的适应度。目标是生成树的长度最小化，因此适应度为该染色体中的Steiner点和正则点求得的最小生成树长度的倒数。

(3) 染色体的选择。利用随机遍历抽样法(Stochastic Universal Sampling，简记SUS)，此方法与轮盘赌选择法基本相似，是对轮盘赌选择法的一种改进，特点是只要进行一次轮盘旋转。其采用均匀分布且个数等于种群规模的旋转指针，等距离选择个体，其中第一个指针位置由[0,1/M]区间的均匀随机数决定，提供了零偏差和最小个体扩展。

(4)染色体的交叉。采用2-opt法进行交叉。需要注意的是，染色体断开的位置必须为3的倍数位置，目的是不把一个点的x、y、z坐标割裂开来。

(5)染色体的变异。随机删除染色体中的一个点的坐标，重新随机选择一个四面体，在其中生成一个随机点加入染色体中。

最终经过若干次的进化迭代，得到适应度最佳的染色体，然后把染色体中度不为3的Steiner点去掉即可。

第三步的结果如图11所示。

图11 示例各部分拓扑结构

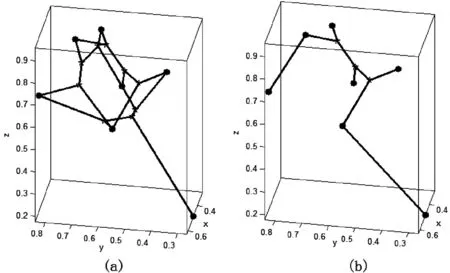
图12 示例结果

第四步 选择适当的满拓扑结构，构成最终解。

第三步中求得的所有满拓扑结构，有些结构共用相同的原点，如图12(a)，所以并不能同时存在于最终解中，因此要选择适当的满拓扑结构来构成最终的解。

在满拓扑结构数量较小的情况下(如10以内的规模)，可使用经典算法，诸如分支定界法或回溯法等，精确地求得应选择哪些拓扑结构。但是在满拓扑结构数量较大的情况下，解空间的大小为2n，其时间复杂度为O(2n)，用经典算法将在计算时间上达到难以容忍的程度，因此，这一步骤依然采用遗传算法进行求解。其中，染色体的长度为满拓扑结构的个数，变量均为布尔型变量，0代表不选择该满拓扑结构，1代表选择该满拓扑结构。

4 实例测试

上述算法在问题规模较小的情况下，如正则点数在10个以内，可省略第一、二、四步，即直接使用遗传算法进行求解，但在问题规模较大时，直接使用遗传算法极易使拓扑结构陷入局部最优，因此，下述实例测试中，分别直接使用遗传算法和本文上述算法进行求解并比较相应结果。

表1 正则点个数为15的实例数据

表2 直接使用遗传算法求得的结果

表3 使用本文算法求得的结果

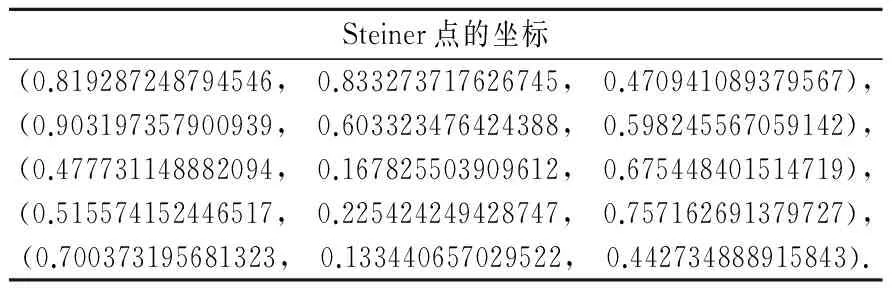
Steiner点的坐标(0.819287248794546, 0.833273717626745, 0.470941089379567),(0.903197357900939, 0.603323476424388, 0.598245567059142),(0.477731148882094, 0.167825503909612, 0.675448401514719),(0.515574152446517, 0.225424249428747, 0.757162691379727),(0.700373195681323, 0.133440657029522, 0.442734888915843).

正则点的最小生成树长度=4.2240，直接使用遗传算法求得Steiner树长=4.1947，使用本文上述算法求得Steiner树长=4.1363

如图13所示，(a)为直接使用遗传算法，仅求得了2个Steiner点，且均为正则点个数为3的满拓扑结构；(b)为使用本文上述算法，求得了5个Steiner点，分别形成了正则点个数为4和5的两个满拓扑结构。

表4 正则点个数为30的实例数据

表5 直接使用遗传算法求得的结果

表6 使用本文算法求得的结果

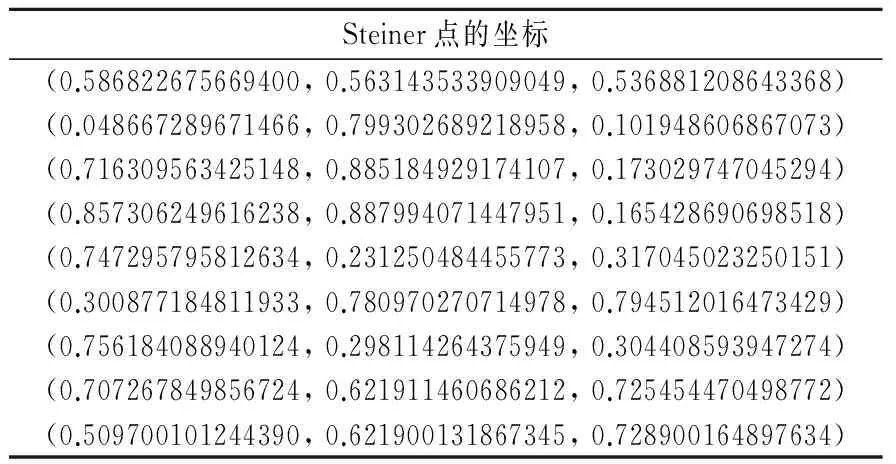
Steiner点的坐标(0.586822675669400,0.563143533909049,0.536881208643368)(0.048667289671466,0.799302689218958,0.101948606867073)(0.716309563425148,0.885184929174107,0.173029747045294)(0.857306249616238,0.887994071447951,0.165428690698518)(0.747295795812634,0.231250484455773,0.317045023250151)(0.300877184811933,0.780970270714978,0.794512016473429)(0.756184088940124,0.298114264375949,0.304408593947274)(0.707267849856724,0.621911460686212,0.725454470498772)(0.509700101244390,0.621900131867345,0.728900164897634)

正则点的最小生成树长度=6.5175，直接使用遗传算法求得Steiner树长=6.4897，使用本文上述算法求得Steiner树长=6.3498

如图14所示，(a)为直接使用遗传算法，仅求得了2个Steiner点，且均为正则点个数为3的满拓扑结构；(b)为使用本文上述算法，求得了9个Steiner点，分别形成了7个满拓扑结构，其中有5个正则点个数为3和2个正则点个数为4的满拓扑结构。

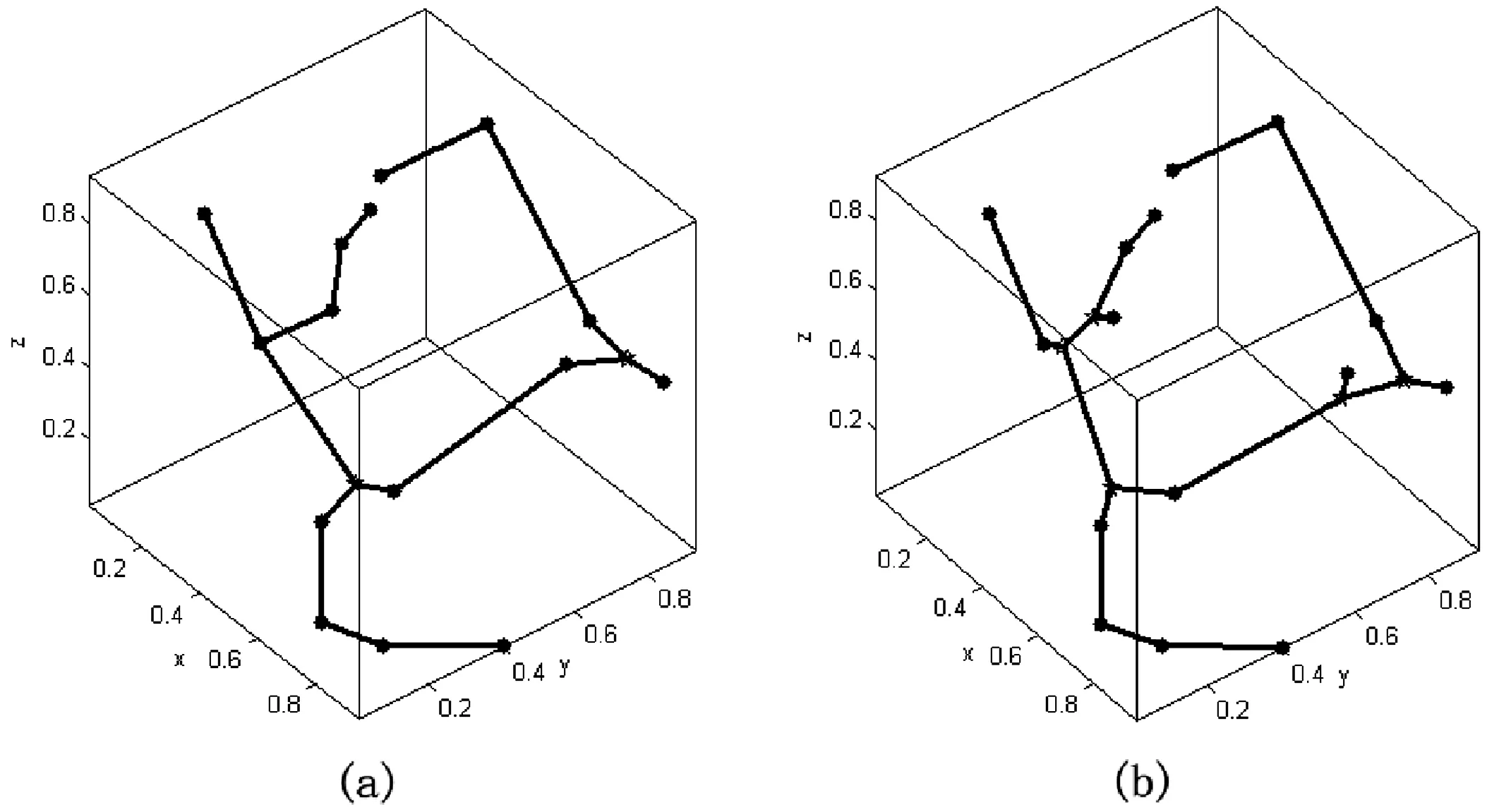
图13 实例测试结果1

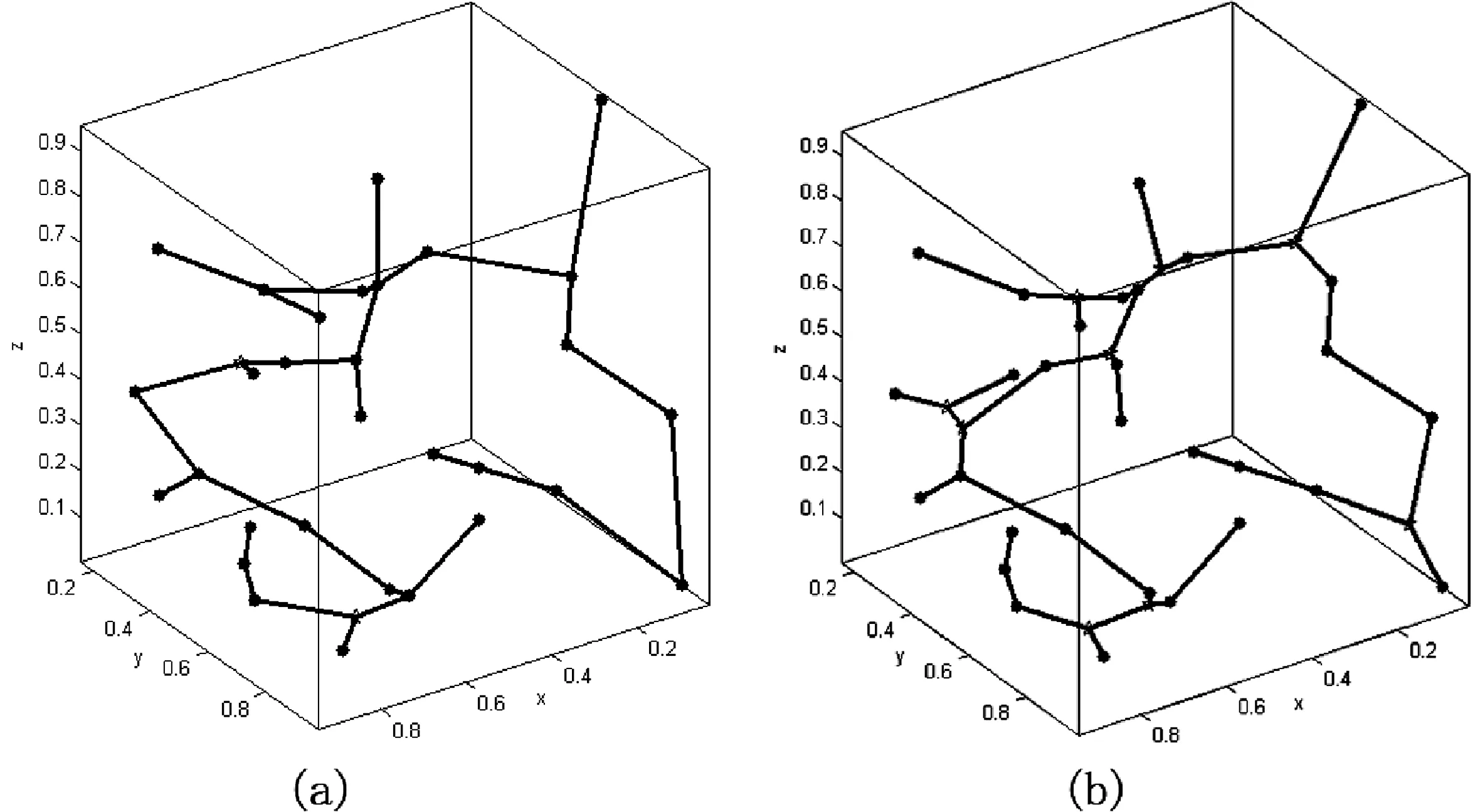
图14 实例测试结果2

5 结束语

经一系列实例测试和结果比较表明，本文给出的混合智能算法在求解三维欧氏Steiner树问题上可以得到令人满意的效果，且在拓扑结构上不易陷入局部最优。整个算法思路简单直观，编程易于实现，对现实中有关实际应用问题的解决提供了方便的求解手段和工具。

[1] 越民义.最小网络——斯坦纳树问题[M].上海:上海科学技术出版社,2006

[2] MacGregor Smith J, Toppur B. Euclidean Steiner minimal trees, minimum energy configurations, and the embedding problem of weighted graphs in E3[J]. Discrete Applied Mathematics, 1996, 71(1-3): 187-215

[3] Smith W D, Smith J M. On the Steiner ratio in 3-space[J]. Journal of Combinatorial Theory, 1995, Series A 69: 301-332

[4] Van Laarhoven, Jon W Ohlmann, Jeffrey W Ohlmann. A randomized delaunay triangulation heuristic for the euclidean steiner tree problem in R-d[J]. Journal of Heuristics, 2011, 17(4): 353-372

[5] 陈学工,潘懋.空间散乱点集Delaunay四面体剖分切割算法[J].计算机辅助设计与图形学学报,2002,14(1):93-95.

A Hybrid Intelligent Algorithm Based on Delaunay Tetrahedron Mesh Generation for Euclidean Steiner Minimum Tree Problem in 3-space

WANG Jia-zhen, MA Liang, ZHANG Hui-zhen

(BusinessSchoolofManagement,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

Euclidean Steiner minimum tree problem, a classical NP-hard problem in combination optimization, has been widely studied in many fields. Euclidean Steiner minimal tree problem in 3-space is the generalization of Euclidean Steiner minimum tree problem in 2-space. The research results on Euclidean Steiner minimal tree problem in 3-space have been rarely published because of their difficulties. In this paper, a hybrid intelligent method is designed by using Delaunay tetrahedron mesh generation technology to solve the Euclidean Steiner minimal tree problem in 3-space, which can not only avoid falling into local optima, but also has good effects in solving large scale problems. Promising results are obtained by using this hybrid method coded in MATLAB to solve series of Euclidean Steiner minimum tree problem instances in 3-space.

euclidean steiner minimum tree problem in 3-space; delaunay tetrahedron mesh generation; convex polyhedron decomposition; intelligent algorithm

2013- 08-22

上海市一流学科建设资助项目(S1201YLXK);上海市教育委员会科研创新项目(14YZ090);高等学校博士学科点专项科研基金联合资助课题(20123120120005);上海高校青年教师培养资助计划(slg12010);上海理工大学博士科研启动项目(1D-10-303- 002)

王家桢(1988-)，女，上海人，硕士研究生，研究方向：智能优化、系统工程；马良(1964-)，男，上海人，博士，教授，博士生导师，研究方向：智能优化，系统工程；张惠珍(1979-)，女，山西忻州人，博士后，讲师，研究方向：智能优化、系统工程。

TP301.6

A

1007-3221(2015)02- 0064- 07