基于动态交易量预测的VWAP算法交易卖出策略

姚海博, 茹少峰, 张文明

(西北大学 经济管理学院,陕西 西安 710127)



基于动态交易量预测的VWAP算法交易卖出策略

姚海博, 茹少峰, 张文明

(西北大学 经济管理学院,陕西 西安 710127)

传统的VWAP交易策略通过预测区间交易量分布进行拆单交易，对于交易量区间分布的预测是基于区间成交量占总成交量比例进行的，这一预测方法没有考虑股票价格变动因素。因此，本文首先通过时间序列因素分解方法进行区间交易量分布预测，进而根据股票价格变化对区间交易量分布进行动态调整，并构建了基于动态区间交易量分布的股票卖出策略，最后通过实证检验了本文给出的动态区间交易量分布预测的有效性和交易策略的有效性。数值结果表明，本文所给动态区间交易量分布预测方法比传统VWAP方法预测结果更加接近于实际的交易量分布，且本文所给交易策略与传统VWAP交易策略相比，具有更大的收益。

算法交易；VWAP卖出策略；交易量分布预测；动态调整

0 引言

算法交易(Algorithmic Trading)是指通过计算机程序来生成交易中的交易时间、交易价格以及交易数量的一种量化交易方式。算法交易中有TWAP、TVOL、VWAP等算法交易策略，其中交易量加权平均价格策略(VWAP交易策略)以其简单易操作的特性而被普遍应用。在证券市场上，大约近 50%的机构投资者的交易订单均采用了VWAP交易策略[1]。

VWAP(Volume Weighted Average Price)是指用当日的股票总成交金额除以当日的总成交量确定的交易均价。传统的VWAP交易策略就是将股票大额交易量，按照预测的日内区间交易量的分布拆分成多个小额交易量进行交易的策略。传统策略对于日内区间交易量分布的预测是根据历史交易量数据采用指数平滑法进行预测，显然这一预测并未将市场的股票价格变动因素考虑在内，从而使其预测的交易量分布偏离股票市场实际交易量分布。本文在基于时间序列因素分解的交易量分布预测的基础上，根据股票价格的变化对预测的区间交易量分布进行动态调整，进而构建基于动态区间交易量分布的股票卖出策略。

关于VWAP交易策略的研究主要集中在区间交易量分布的预测问题上，CHRISTIAN T. BROWNLEES等人提出了一种基于时间序列因素分解的乘法误差模型，通过该模型进行了股票市场交易量的预测，并通过实证检验了该预测方法应用于VWAP交易策略的有效性[2]；魏文婷利用主成分分析方法对中国证券市场成交量进行了动态分解建模，并通过模型对日内成交量进行了预测，然后将该模型应用于 VWAP算法策略，最后得出了交易的执行成本比传统方法显著降低的结果[1]；罗业华等人使用高频数据从交易量预测层面对VWAP策略进行了模拟和优化，得出了日内交易量分布预测的准确性对VWAP策略影响较大的结论[3]。以上的研究都是以交易量分布的预测为基础展开的，而从交易策略改进的角度进行研究的学者有：曹力等人利用价格信息提出一种改进的VWAP策略，该策略通过分析交易日内各个决策点前的股票价格变化，来对传统VWAP策略的决策进行调整，从而提高了执行的效果及稳定性，并节省了交易成本[4]；Cheng Der Fuh等人提出了一种基于统计仿真的价格交易量模型，并通过动态策略来捕捉价格的波动性[5]；镇磊利用高频数据处理方法提出了一种适合A股市场交易规则的交易算法，以及一种基于自相关的分时的 VWAP算法，并实证检验了其有效性[6]；林辉等人通过放松理想化市场的假设条件，通过构建流动性调整的最优交易策略模型，证明了交易策略在任意初始持仓、不同行情时的性质[7]。

通过以上综述可以看出，VWAP交易策略有效性的关键在于对区间交易量分布的预测。本文首先通过时间序列因素分解的方法进行交易量的预测，然后根据股票价格因素对预测的交易量进行动态调整，进而构建了基于动态区间交易量分布的股票卖出策略。

1 区间交易量的分布预测模型

1.1 股票区间交易量的分布预测模型

本文将第t天的交易时间划分成M个区间，用ytm表示第t天第m区间的总交易量，m=1,…,M，则股票第t天的交易量可以由(yt1,yt2,…,ytm,…,ytM)组成的时间序列表示。如果考虑连续k天的股票交易量，则k天的股票交易量组成一个面板数据，用数学方法可以表示为：

(1)日内交易量时间序列的分解模型

对日内区间交易量时间序列的分解乘法模型：

ytm=ηt×ψtm×μtm

其中ytm为第t天的第m个区间内的交易量，ψtm表示日内数据的周期因素，ηt表示日间数据的趋势因素，μtm表示日内数据的波动因素。

用φtm表示第t天第m区间内的交易量与该日交易量均值的比例，用φkm表示从第1天开始，连续k天φtm的平均值，用ψkm表示第k天第m区间的周期因素，计算公式分别为：

用ηt表示日间数据的趋势因素，用μtm表示日内数据的波动因素，计算公式分别为

(2)日内交易量分布的预测模型

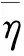
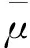
本文选取第k+1天的周期因素为ψk+1m，且令ψk+1m=ψkm。

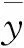
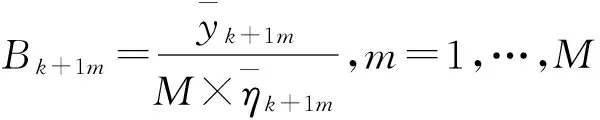
1.2 股票交易量分布的动态调整

区间交易量分布的调整原则为：在股价上升阶段相应增加股票的交易量，在股价下降阶段则相应的减少交易量，在股价平稳阶段则不改变交易量，具体调整算法如下：

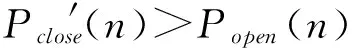
根据以上规则对每一个预测区间内的交易量分布进行调整，得到调整后的交易量的分布为Fk+1n。

1.3 动态交易量分布预测的实证检验

(1)数据来源及数据处理

表1 本文所选的样本股票的名称及股票代码列表

(2)预测模型中的平滑系数和步长的确定

在实证研究中对于日间趋势因素、日内波动因素采用指数平滑预测，其平滑系数确定方法如下：

根据文献[8]对于指数平滑法中平滑系数选择的研究认为：对波动较大的时间序列平滑系数应该取在0.3～0.5之间，对波动较小的时间序列平滑系数应取在0.1～0.3之间。在本文中，对趋势因素进行方差检验，其波动较大，所以选取α为0.5；对于波动因素μkm进行方差检验，其波动较小，所以选取β为0.3。

在对于日内周期因素的计算中，k值的确定方法为：

本文以表1中各只股票2012年前100个交易日数据为样本，在样本区间内选取不同的k值，k∈{2,3,4,…,99}，通过编译MATLAB程序计算100个交易日内各股预测的k+1天的交易量分布的平均绝对误差的均值，最终选择出使预测的平均绝对误差的均值最小的k值作为选取样本的天数。此处仅展示以浦发银行、华夏银行2012年数据为例的实验结果，如图1所示：

(a)浦发银行2012年数据取不同k值时预测的平均绝对误差的均值结果

(b)华夏银行2012年数据取不同k值时预测的平均绝对误差的均值结果图1 k取不同值时预测的平均绝对误差的均值

如图1所示，随着k值的增加，预测的平均绝对误差的均值在逐渐减小，而在k取值大于30以后，预测的平均绝对误差的均值降低的幅度不再增加，故本文选定k=30。

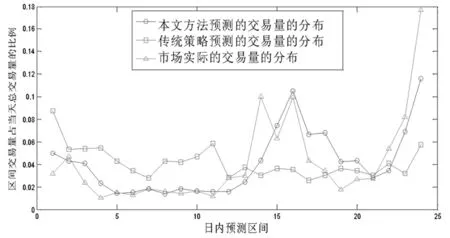
图2 浦发银行2012年2月24日的交易量分布

(3)实证结果

本文随机选取浦发银行股票2012年2月24日的交易量分布并进行预测，预测结果如图2所示。

从图2可以看出，本文给出的交易量分布预测算法较传统算法更加接近于市场实际的交易量分布。

本文进一步对表1中的股票在选取k日样本后的全年剩余的交易日内，连续进行交易量分布的预测。并与传统预测方法进行比较。令MAD1表示本文方法预测值与市场实际值的平均绝对误差，MAD2表示传统策略预测值与市场实际值的平均绝对误差。则通过比较各股所有预测天的MAD1与MAD2的均值与方差来判断本文预测方法与传统策略预测方法对交易量分布预测的准确性。结果如下：

表2 股票的MAD1、MAD2的均值和方差

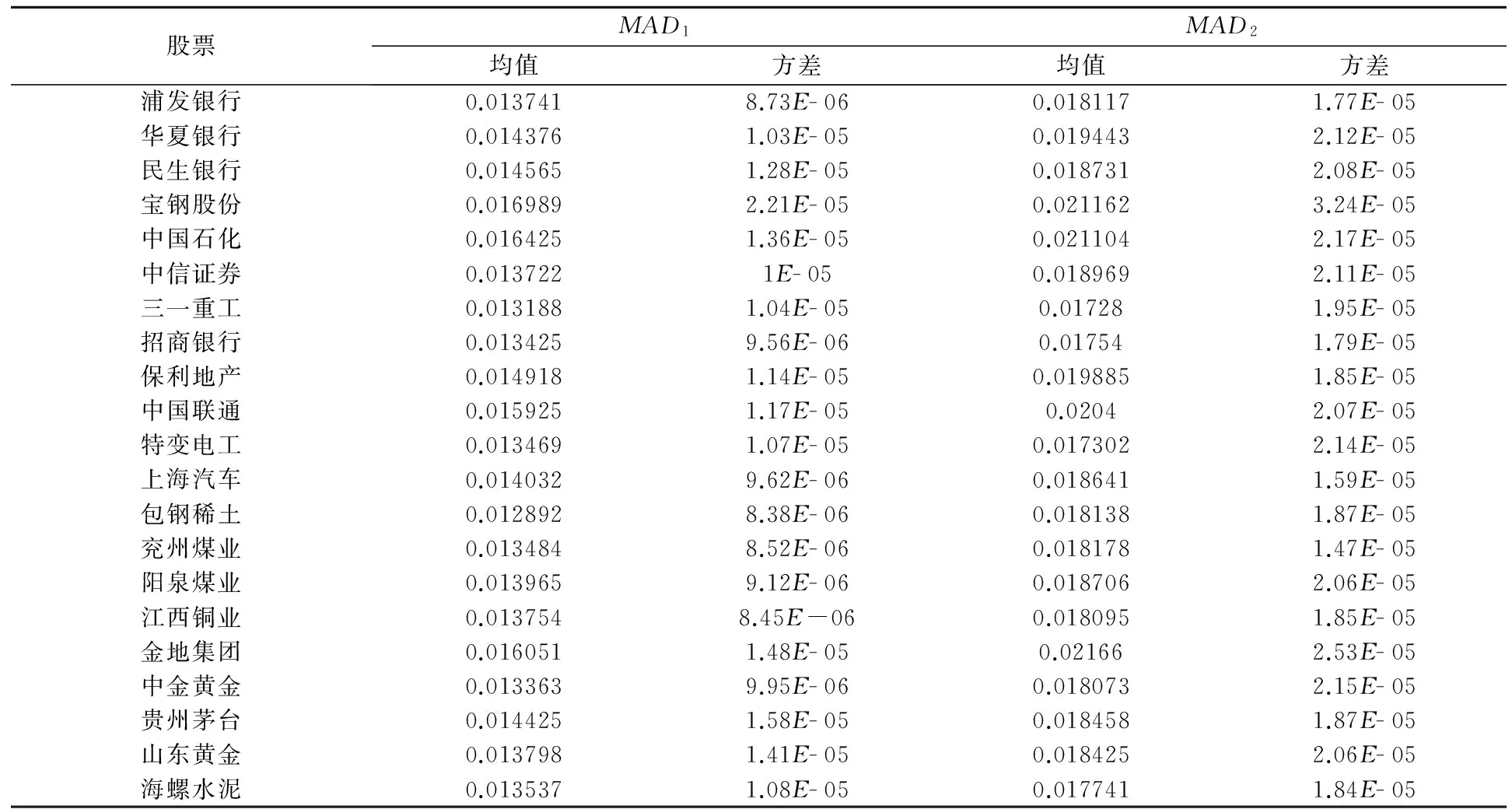
股票MAD1MAD2均值方差均值方差浦发银行0.0137418.73E-060.0181171.77E-05华夏银行0.0143761.03E-050.0194432.12E-05民生银行0.0145651.28E-050.0187312.08E-05宝钢股份0.0169892.21E-050.0211623.24E-05中国石化0.0164251.36E-050.0211042.17E-05中信证券0.0137221E-050.0189692.11E-05三一重工0.0131881.04E-050.017281.95E-05招商银行0.0134259.56E-060.017541.79E-05保利地产0.0149181.14E-050.0198851.85E-05中国联通0.0159251.17E-050.02042.07E-05特变电工0.0134691.07E-050.0173022.14E-05上海汽车0.0140329.62E-060.0186411.59E-05包钢稀土0.0128928.38E-060.0181381.87E-05兖州煤业0.0134848.52E-060.0181781.47E-05阳泉煤业0.0139659.12E-060.0187062.06E-05江西铜业0.0137548.45E-060.0180951.85E-05金地集团0.0160511.48E-050.021662.53E-05中金黄金0.0133639.95E-060.0180732.15E-05贵州茅台0.0144251.58E-050.0184581.87E-05山东黄金0.0137981.41E-050.0184252.06E-05海螺水泥0.0135371.08E-050.0177411.84E-05

从表2的数据可以看出MAD1的均值均小于MAD2的均值，说明本文预测方法的预测结果较传统策略更加准确；MAD1的方差均小于MAD2的方差，说明本文预测方法的稳定性优于传统策略。

2 基于动态交易量预测的VWAP卖出策略

2.1 基于动态交易量的VWAP卖出策略设计

假设交易股票量为V=10000股，且可以按任意股数卖出。将日内的交易时间划分为N个区间，且N=M/2，根据上文给出的动态交易量分布预测结果，将股票量V分配在N个交易区间内。规定在每个交易区间末的时点上，按照卖出价格Pclose(n)，卖出的股票量为Vk+1n=Fk+1n×V进行交易。并假定交易可以实现，交易过程中没有交易费用。交易直至股票全部卖出为止。

2.2 卖出策略的实证检验

(1)数据来源及数据处理

此处依然选用上文表1中的股票，数据中成交量是5分钟内所有交易量之和，价格包括5分钟内的开盘价和收盘价。日内交易区间为24个，即N=24。以k个交易日为交易量分布预测的样本数据，预测第k+1个交易日内的交易量的分布，并进行交易，按此方法逐次递推，在各股第k个交易日以后的全年剩余交易日内进行交易。与上文相同，k取30天。

(2)实证结果

我们对表1中各股从2012第一个交易日开始，在选取的k个样本交易日以后的全年剩余交易日内进行交易。此处仅展示本文策略得到的浦发银行、华夏银行全年交易的VWAP价格，如下所示：

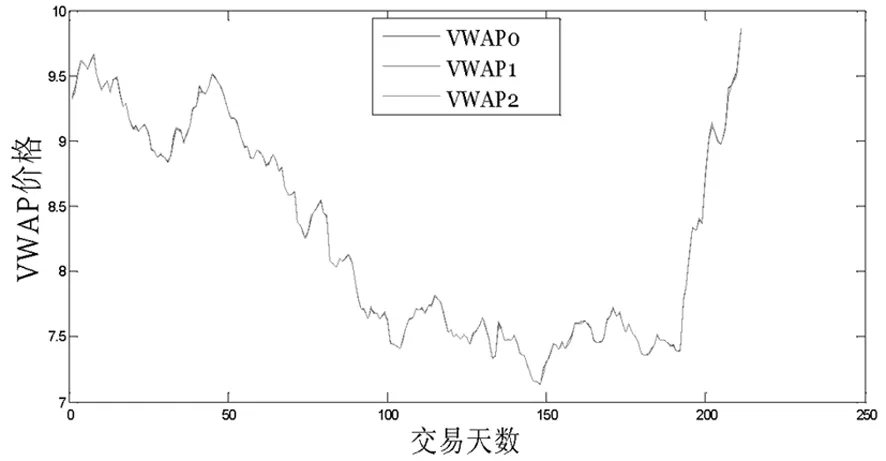
2012年浦发银行全年的VWAP交易价格

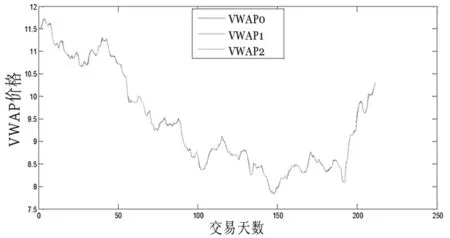
2012年华夏银行全年的VWAP交易价格图3 股票全年交易的VWAP交易价格

其中，本文策略得到的交易量加权平均价格序列为VWAP1，传统策略得到的交易量加权平均价格序列为VWAP2，市场实际的交易量加权平均价格序列为VWAP0。从图3可以看出，本文策略得到的VWAP交易价格更加接近于市场实际的VWAP价格。

(3)实证结果的比较

通过表3，在所选的21只股票中，VWAP-MAD1均小于VWAP-MAD2，说明本文得到的VWAP价格较传统策略得到的VWAP价格更加接近于市场实际的VWAP价格，证明了本文策略的有效性。从收益差值来看，除贵州茅台收益差值为负值-119836.00，其余股票的收益差值均大于0，收益差值最大值为包钢稀土98065.02，差值的均值为11294.04。综上，可得本文策略得到的VWAP价格与市场实际的VWAP价格的偏差更小，而且从平均水平上，本文策略与传统策略相比，可以获得更大的收益。

表3 股票的VWAP价格平均绝对误差及收益差值

3 结束语

传统的VWAP交易策略对于交易量区间分布的预测是基于区间成交量占总成交量比例进行的，并没有考虑股票价格变动因素。因此，本文首先通过时间序列因素分解方法进行区间交易量分布预测，进而根据股票价格变化对区间交易量分布进行动态调整，并构建了基于动态区间交易量分布的股票卖出策略。最后通过选取上证50指数中的21只股票，实证检验了本文给出动态区间交易量分布预测的有效性和交易策略的有效性。数值结果表明，本文所给动态区间交易量分布预测方法比传统VWAP方法预测结果更加接近于实际的交易量分布，且本文所给交易策略与传统VWAP交易策略相比，具有更大的收益。

[1] 魏文婷.中国证券市场成交量动态建模及VWAP算法应用改进[D].天津:天津大学硕士学位论文,2009,(5):1-3.

[2] Christian Brownlees T, Fabrizio Cipollini, Giampiero Gallo M. Intra-daily volume modeling and prediction for algorithmic trading[J]. Journal of Financial Econometrics, 2011, 9(3): 489-518.

[3] 罗业华,杨向阳,徐静,陈军华.VWAP策略在A股交易中的应用——交易优化策略专题研究报告(3)[R].招商证券,2012(3).

[4] 曹力,曹传琪,邵立夫.改进型VWAP策略及实证——算法交易系列研究之三[R].联合证券,2010,(1).

[5] Cheng Der Fuh, Huei Wen Teng, Ren Her Wang. On-line VWAP trading strategies[J]. Sequential Analysis:Design Methods and Applications, 2010, 29(3): 292-310.

[6] 镇磊.基于高频数据处理方法对A股算法交易优化决策的量化分析研究[D].安徽:中国科学技术大学博士学位论文,2010,(5).

[7] 林辉,张涤新,杨浩,丁一.流动性调整的最优交易策略模型研究[J].管理科学学报,2011,(5):65- 67.

[8] 王长江.指数平滑法中平滑系数的选择研究[J].中北大学学报(自然科学版),2006,(6):558-561.

VWAP Algorithm Selling Strategy Based on Dynamic Trading Volume Forecast

YAO Hai-bo, RU Shao-feng, ZHANG Wen-ming

(SchoolofEconomicsandManagement,NorthwestUniversity,Xi’an710127,China)

The traditional VWAP trading strategy trading volume depends on the distribution of split single transaction, and the forecast of the distribution of trading volumes is based on the interval volume proportion of the total volume, and this prediction method does not consider the stock price changes. Therefore, by means of the time series factor decomposition the paper first predicts the distribution of trading volumes, then based on the stock price changes in the distribution of trading volumes adjust the trading volume distribution of dynamic ranges and builds the stocks selling strategy by the trading volume distribution, and finally, through an empirical test in this paper, tests the predictive validity and effectiveness of the distribution of trading volumes. Numerical results show that the prediction method of the distribution of dynamic volumes given in this paper is better than the traditional VWAP method and the results of the new method are much closer to the distribution of the actual transaction volume. And compared with the traditional VWAP trading strategy, the strategy given in this paper is more gainful.Key words:algorithmic trading; VWAP selling strategy; trading volume distribution prediction; dynamic adjustment

2013- 06-26

国家自然科学基金青年项目(71201123);“基于在线时间序列搜索的算法交易策略研究 ”；陕西省自然科学基础研究计划项目(2014jq8367)：“股票时间序列大数据挖掘与分析研究”；西北大学科学研究基金项目(11NW04)。

姚海博(1988-)，男，硕士，研究方向：算法交易；茹少峰(1962-)，男，教授，研究方向：运筹与管理；张文明(1984-)，男，讲师，研究方向：算法交易。

F830.91

A

1007-3221(2015)02- 0215- 06