随机交通网络渐近连通可靠性分析

马洪伟, 周溪召

(1.上海海事大学 经济管理学院，上海 200135； 2.上海电机学院 商学院，上海 201306)



随机交通网络渐近连通可靠性分析

马洪伟1,2, 周溪召1

(1.上海海事大学 经济管理学院，上海 200135； 2.上海电机学院 商学院，上海 201306)

应用原有拓扑法获得城市交通网络的拓扑结构图,利用对偶拓扑法得到交通网络的对偶图，建立交通网络的随机网络模型。定义交通网络的渐近连通可靠性，得到路段连通可靠性、路网规模及整个路网连通可靠性之间的定量关系，结合随机图论、大数定律、渐近方法等证明所得结论；通过实例说明结论的应用价值。

随机交通网络；渐近连通；可靠性；对偶拓扑法

0 引言

自然灾害和交通拥堵使人们越来越重视交通运输网络的可靠性，目前对城市道路网络可靠性研究主要有三类：通行能力可靠性、行程时间可靠性和连通可靠性。其中，连通可靠性是交通网络可靠性分析研究的基础，只有在连通的基础上才能确保各类交通流完成出行。

连通可靠性反映的是交通网络节点两两间保持连通的概率，它是进行其它可靠性分析的研究基础，最早是由日本的Mine Kawai在1982年提出的[1]，随后，各国学者作了进一步的理论探讨[2,3]。早期连通可靠性研究的对象主要是系统的物理结构，考虑的是系统连通性，连通可靠性一般只有0,1两种状态，1代表连通，0代表不连通。城市的交通状态是随机变化的，仅用两个变量不能反映交通网络连通的不断变化，常态环境下城市道路连通性有多种状态。朱顺应、陈晓明、吕斌等采用饱和度法(v/c)来刻画路段连通可靠性的状态，连通的概率是流量v和通行能力c的函数，p=F(v,c)，这样连通可靠性由{0,1}扩展到[0,1]区间[4～6]，这种扩展使连通可靠性的应用范围更广；但同时又面临新的问题，虽然通过标定函数可以求得F(v,c)路段的连通可靠性，但由于交通网络的结构往往比较复杂，规模过大，整个交通网络连通可靠性的定量研究会变得非常困难。因此，路段连通可靠性、路网规模及整个路网系统的连通可靠性之间的关系一直没有定论。

本文在道路状态影响因素方面主要考虑交通流量和通行能力。连通可靠性是流量和通行能力的函数，即连通可靠性p=F(v,c)，p∈[0,1]；用对偶拓扑法获得交通网络图，定义随机交通网络的渐近连通可靠性，利用随机网络模型研究路段连通可靠性、路网规模及路网连通可靠性之间的定量关系，在一定条件下一定程度上解决两个基本问题：a.当路段连通可靠性较小的状态下(交通拥堵状态或路段遭到毁坏)，路网是不是仍然保持连通的；b. 路网结构和规模确定条件下，路段连通性和整个路网连通性之间的定量关系，即路段的连通概率为多少时才能保证整个路网是连通的。

1 交通网络的随机网络模型

1.1 交通网络拓扑结构图的获得

交通网络连通可靠性分析首要问题是利用一定的规则处理现实中的交通网络。一个交通网络由交叉口和路段(或称为边) 组成，常用刻画静态交通网络的网络拓扑方法主要有:原有拓扑法，以边为拓扑结构的边，交叉口为节点；对偶拓扑法，以道路编号或者路名为节点，即相同的路名可用一个节点代替，交叉口为节点之间的连线。利用对偶拓扑法转化路网的拓扑图实质是进行点和边的相互转化来表达网络的连通性。在进行边转化为点时，原图中一条边就转化为对偶图中的一个点，而在点(交叉口)转化为边时，要根据网络的连通性而定，通过转化原图中边和交叉口的连通概率完全转化为对偶图中边出现的概率。

本文首先利用原有拓扑法建立交通网络图，然后通过不同路段交通流量和通行能力整合网络图，合并交通流量v和通行能力c接近的路段，拆分交通流量和通行能力差别过大的路径。具体做法，设定两个阈值l和∂，对具有同一路名的不同路段s和t，若满足|vs-vt|>l或|cs-ct|>∂，则在网络图中路段s和t作为两条边看待，否则可把路段s和t合并为一条边；对不同路名的相同方向路段s和t若|vs-vt|≤l且|cs-ct|≤∂，则两条道路s和t在网络图中视为一条边。经过上述整合之后，再利用对偶拓扑法可以得到所需要的交通网络图。

1.2 城市交通网络的随机网络模型

利用上述方法得到一个交通网络图G(A,E)，其中A={a1,a2,…,ai,…,an}表示对偶图中节点的集合，实际代表路网道路的集合；记E={e1,e2,…,ei,…,en}为对偶图中边的集合，实际表示交通网络中道路的连通关系。以下讨论皆在G(A,E)对偶图中进行。若要确定网络图G(A,E)的连通性，需要确定网络图G(A,E)是以何种结构出现的，即图G(A,E)的边生成规律。

对交通网络的结构研究，多是结合规则网络、无标度网络或随机网络等相关模型，这类方法从静态角度刻画了交通网络的平均距离、度分布、连通性等几何特征，静态网络模型在刻画交通网络连通性随时间变化特性方面显得不足，特别是现实中随着交通需求增大，拥堵加剧；交通需求随机性对连通性的影响主要反映在图G(A,E)中边出现的概率，本文的研究基础是基于随机网络模型，网络图G(A,E)中边的集合E={e1,e2,…,ei,…,eq}中每条边的出现，也就是任何两点连接成边以概率p出现，并且每两点连接形成边是独立的，相比而言这种模型能较好的反映交通网络连通性的随时间变化的规律。

2 交通网络渐近连通可靠性定义

以下分别从两个角度，定义交通网络的渐近连通可靠性。

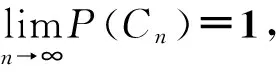
定义2：随机交通网络G(A,E)，G(A,E)的顶点n为常数，G(A,E)中任意两点连通的概率(也是每条边出现的概率)为p，若存在p0，当p≥p0时，随机交通网络G(A,E)是连通的，当p≤p0时，随机交通网络G(A,E)是不连通，称交通网络G(A,E)具连通概率变大时的渐近连通可靠性，同时称P0为随机交通网络G(A,E)连通可靠性的阈值。

从定义1得知，若交通网络具有网络规模变大时的渐近连通可靠性，当网络规模大到一定程度时，即使连通的概率很小，交通网络仍然是连通的。由定义2知，当交通网络规模一定时，路段连通的概率不同，整个交通网络可能连通，也可能不连通；特别的，在满足随机网络模型条件下，一定存在交通网络连通可靠性的阈值，交通网络是具有渐近连通可靠性的。下面结合ER随机图模型[7,8]，给出阈值的具体表达式。

3 交通网络渐近连通可靠性证明

结合两种定义给出三个结论，并进行证明。

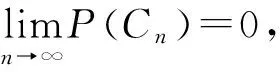
以上结论说明当随机交通网络的规模大到一定程度时，虽然某些道路是不连通的，但整个交通网络是连通的，结论2没有说明达到何种程度；从另一个角度考虑，如果网络规模确定，连通的概率p增大到某种程度也能保证交通网络是连通的，至于p要达到何种程度，结论3在一定程度上给予解决。

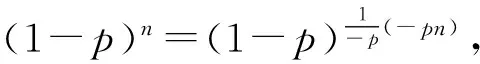
需要证明存在孤立的节点的概率收敛于1。

先证xn的方差是有界的：考虑E[(xn)(xn-1)]是孤立节点有序对的期望个数，因此，E[(xn)(xn-1)]=n(n-1)(1-p)2n-3。xn的方差

=n(n-1)(1-p)2n-3+E(xn)-n2(1-p)2n-2

≤E(xn)+pn2(1-p)2n-3≤E(xn)(1+(lnn-f(n))e-lnn+f(n)(1-p)-2)

=2E(xn)

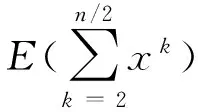
(1)

分别考察(1)式的前后两项，对(1)式的第一项：

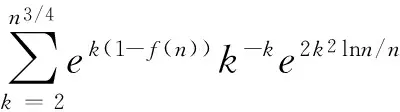
∵e-f(n)<1，e2n-1/4lnn<1，∴(e-f(n)e2n-1/4lnn)2<1，即(1)式的第一项小于1；对(1)式的第二项

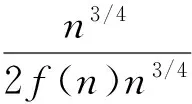
∴e(1-f(n)/2)n3/4n(-1/4)n3/4→0，即(1)式的第二项趋于0；

4 交通网络渐近连通可靠性的应用示例

如图1所示，为宁波市高新区交通网络图，利用本文第1.2中的方法，根据某一时段的交通流量和通行能力对路段进行整合，利用对偶图法得到所需网络图如图2。图2由39个顶点，236条边构成，顶点代表道路，边代表39条道路之间的连通关系。由随机网络模型求得，宁波高新区交通网络对应边的连通可靠性约为0.2，有39个点构成的随机网络，连通的阈值为ln39/39=0.093，所以，当道路畅通的情况下，边与边的连通概率较大，此时整个交通网络具有较好的连通性。但当边的连通概率降低时，整个路网的连通可靠性也会降低，如当连通的概率为0.1时，得到的随机网络图为图3，此时就会出现孤立点，孤立点存在表示道路是不连通的。

图1 宁波高新区交通网络原始图

图2 宁波高新区交通网络对偶图

图3 连通概率为0.1时对应的随机网络图

5 结语

本文利用对偶拓扑法得到交通网络的网络拓扑图，构建起交通网络的随机网络模型，从两个角度，分别定义交通网络的渐近连通可靠性，得出两个结论，当路段连通可靠性为常数时，网络达到一定规模，整个路网是连通的；当路网规模确定时，可以通过提高路段的连通可靠性方法，提高整个交通网络的连通可靠性。本文所得出的结论在路网规划设计方面，从交通网络行驶时间可靠性视角为城市交通网络节点规模的合理确定提供依据，也可避免城市规模无限制扩张；在日常交通管理方面当交通网络某个路段的交通流量达到一定的阈值时，需要重点关注，为交通管理和控制提供帮助。

本文的研究是基于随机网络模型得到的，有一定的局限性，城市交通网络每条道路的连通概率不可能完全相等，因此，不同道路的连通概率将构成向量P=(p1,p2,…pi…,pN)，显然，当min{p1,p2,…pi…,pN}≥lnn/n时，结论3成立，对于min{p1,p2,…,pi,…,pN}≤lnn/n时，整个交通网络的连通可靠性会变得更加复杂，需要继续深入研究。

[1] Mine H, Kawai H. Mathematics for reliability analysis[M]. Asakurashoten, 1982. 12-14;

[2] Bell M G H, Iida Y. Transport network analysis[M]. NewYork: John Wiley & Sons, 1997. 179-191.

[3] Alan Nicholson, Zhen-Ping Du. Degradable transportation systems: an integrated equilibrium model[J]. Transportation Research B .Vol 3, 1997. 209-223.

[4] 朱顺应,王炜,邓卫,唐勇,王波.交通网络可靠度及其通路算法研究[J].中国公路学报,2000,13(1):91-94.

[5] 陈晓明,邵春福,熊志华.混合交通信号交叉口的通行能力可靠度[J].中国公路学报,2008,21(4):99-104.

[6] 吕斌,牛惠民.信号控制交叉口可靠度建模与仿真[J].交通运输系统工程与信息,2011,11(6):45-50.

[7] Bollobas B. Modern graph theory[M]. New York: Springer-Verlag, 2001.

The Asymptotic Connect Reliability Analysis of Stochastic Transportation Network

MA Hong-wei1,2, ZHOU Xi-zhao1

(1.School of Economics and Management, Shanghai Maritime University, Shanghai 200135, China; 2.Shanghai Dianji University, Shanghai 201306, China)

The topology map of urban transportation network is gained by using the original topological method, the dual graph of the transportation network is gotten by using the dual topology method, and the random network model of transportation network is thus established. The asymptotic connectivity reliability of the transportation network is defined, and what is be gained is the quantitative relationship among road connectivity reliability, scale of the road network, and the connectivity reliability of the entire road network. The conclusions in this paper are proved by combining the random graph theory with law of large numbers, asymptotic methods and so on. Finally, the application value is illustrated through an example.

stochastic transportation network; asymptotic connectivity; reliability; dual topology method

2013- 08-28

国家自然科学基金资助项目(61273042)；上海市教育委员会科研创新项目(BYS125);上海海事大学研究生创新基金资助项目(YC2011046)

马洪伟(1982-),男，山东枣庄人，博士研究生,理学学士,工学硕士；周溪召(1964-),男，浙江宁波人，教授、博士生导师，理学硕士，工学博士。

U113

A

1007-3221(2015)03- 0045- 06