密封第一价格拍卖中的竞拍者串谋分析
——基于“强”卡特尔的第一价格预拍
2015-07-07林菡密孙绍荣
林菡密, 孙绍荣
(1.上海理工大学 管理学院,上海 200093; 2.杭州师范大学 钱江学院,浙江 杭州 310036)
密封第一价格拍卖中的竞拍者串谋分析
——基于“强”卡特尔的第一价格预拍
林菡密1,2, 孙绍荣1
(1.上海理工大学 管理学院,上海 200093; 2.杭州师范大学 钱江学院,浙江 杭州 310036)
已有密封一价拍卖竞拍者串谋均衡研究中存在不符合现实的诸多约束,鉴于此,在串谋只包含部分竞拍者、串谋成员与非串谋尔成员间形成独立、非对称以及连续的价值分布并同时存在竞价策略互动的假设下,建立串谋方和非串谋方互动的竞价优化模型以及拍卖方的保留价格优化模型,得到串谋方和非串谋方的最优竞拍出价以及竞拍方的最优保留价格。结果表明串谋方和非串谋方的出价策略不仅与自身的估价、竞标人数、串谋人数相关,也与对方的估价存在关联性;拍卖方的最优保留价格设定与非串谋方和串谋方的价值分布存在关联。
第一价格预拍;“强”卡特尔;竞拍者串谋;非对称性;保留价格
0 引言
拍卖在经济领域的广泛应用,引起了许多学者的重视,近年来有不少拍卖方面的科研成果[1~3],然而这些成果都是基于标准拍卖模型,即假设拍卖中不存在串谋问题,然事实是不管拍卖方采取何种拍卖方法,都存在竞拍者串谋现象,只是不同的拍卖机制下串谋的稳定性不同。理论上,第一价格密封拍卖比第二价格密封拍卖[4~8]更不容易产生串谋[9~12],因此在在实践上,第一价格密封拍卖也被广泛应用于各种采购事物中,但Porter & Zona[13,14]、 Bajari and Ye[15]、Gaurab and Maria[16]采用贝叶斯方法、非参数检验方法等不同的方法检测到第一价格密封拍卖拍卖在高速公路建设、学校牛奶采购、小麦拍卖等各行业应用中确实存在竞拍者串谋现象。研究充分表明,通过一价拍卖或者二价拍卖的预拍机制确定串谋组织在正式拍卖中的竞拍代表,并在正式拍卖中采用控制非竞拍代表的串谋合作者的竞拍出价以保证串谋收益的实现[17~19],同时以强制执行地区分配(territory allocation)、轮流坐桩(bid rotation)、虚假(互补)出价(phony bidding)等手段以维持组织内部的稳定性。
第一价格预拍串谋机制有着与第二价格预拍不同的性质,从而决定了第一价格预拍更具研究难度:首先,第一价格预拍的串谋机制不是激励相容的,无法自我实施,此时的串谋组容易遭致背叛从而使得串谋不稳定。为了简要说明这一点,考虑所有竞拍者都参与了串谋。假设最高价值大于拍卖方设定的保留价格,串谋组织可以只提交一份等于保留价格的报价,并确保其他报价都不超过这个数目,从而以保留价格获得物品。现在考虑某个竞拍者,他的价值在保留价格以上,却不是最高的,因此,他就有激励去采取偏离协议规定的行动,以刚刚超过保留价格的报价赢得该物品。其次,第一价格预拍的串谋机制运作会自然在串谋方和非串谋方之间引入不对称性[14](假使串谋不存在时,所有竞拍者事先是对称的。),从而使得串谋方和非串谋方的出价策略发生了变化。而在第二价格预拍中则不存在这种情况,按价值出价仍然是占优策略,串谋方的存在也不会影响非串谋方的策略。
McAfee and McMillan[20]、Marshall and Marx[21]、Lopomo and Marx[19]和敬辉蓉[22]都对第一价格预拍做出了一定研究。文献[20]设计了两种第一价格预拍下的串谋机制——强卡特尔和弱卡特尔(强卡特尔可以在组织内部进行转移支付而弱卡特尔则不行),在假设正式拍卖中存在一个包含了所有潜在竞拍者的串谋团体(且人数确定)的条件下,证明了强卡特尔和弱卡特尔下的最优串谋机制。强卡特尔的最优机制是在组织内进行预拍卖,获胜者在正式拍卖中以保留价格出价,而其他成员则不参与竞标,获胜者将预拍卖中的报价通过转移支付分配给其他卡特尔成员;弱卡特尔的最优机制是所有竞标者以统一价格出标,并不进行转移支付。文章的最后也考虑到了卡特尔不一定能包含所有的竞拍者的现实情况,并对卡特尔只包含部分潜在竞标成员的情况进行了简略的分析:(1)非串谋成员考虑到串谋方的存在,对串谋方的出价做出策略性反映。(2)所有竞拍者的对拍卖物品的估价是在区间[0,1]上的离散分布,而没有考虑到连续分布的情况,而且所有成员的估价是对称的。文献[21]在文中提出了BCM(bid coordination mechanism)和BSM(bid submission mechanism)两种预拍机制——BCM机制规定卡特尔内部能进行转移支付并且为串谋成员建议出价,但是没有权利控制竞拍者的出价。BSM机制中规定卡特尔有权利控制串谋成员的出价,其中一种解释就是卡特尔选出一位代表参加正式拍卖并能阻止其他串谋者参与竞拍。作者主要研究了两种拍卖机制在第一价格密封拍卖和第二价格密封拍卖下的生存能力和收益性。文献[19]进一步证明BCM机制在第一价格拍卖中虽然无法增加收益但一定能保证串谋的稳定性。文献[22]研究了第一价格预拍“强”卡特尔串谋机制中,串谋方在预拍卖和正式拍卖中的最优报价。
综上,关于第一价格预拍的研究存在以下几点不足:(1)主要考虑卡特尔包含了所有潜在的竞拍成员情况;(2)当考虑到卡特尔没有包含所有竞拍者时,认为非串谋成员会对串谋成员做出策略性反映,但是所有竞拍者的对拍卖物品的估价是在集合{0,1}上的离散的对称分布,而没有考虑到连续的非对称分布的情况;(3)在密封第一价格正式拍卖中,串谋方和非串谋方之间并未形成策略互动。
本文在以往研究的基础上,以基于“强卡特尔”第一价格预拍的第一价格密封正式拍卖中的竞拍者显性串谋机制为研究对象,关注正式拍卖中事实情况——卡特尔并不总能包含所有竞拍成员,此时非串谋成员和串谋成员一般会考虑对方的存在而形成竞价策略上的互动,并且串谋方与非串谋方之间的价值分布是非对称且连续的——的基础上,主要考察了以下二个问题:(1)采用非对称拍卖均衡的视角研究串谋方与非串谋方在正式拍卖中互动的竞拍出价规律;(2)拍卖方针对竞拍者可能存在的串谋行为从保留价格上采取的策略响应。
1 预拍卖、正式拍卖的执行过程及其假设条件
1.1 预拍卖、正式拍卖的执行过程
本文设计的拍卖存在两个阶段,第一阶段为正式拍卖之前的价格串谋预拍卖,串谋方能够正常运作的前提是选择并执行一种价格串谋的机制,本文采用的是“强卡特尔”第一价格预拍的串谋机制,该串谋机制的具体实施如下:考虑存在一个协调串谋组织活动的中心执行已经确定的强卡特尔下的第一价格预拍预拍机制,特定的内容包括:①将代表串谋方出席正式拍卖活动的权利分配给具有最高估价的成员;②确定代表成员应支付给中心的转移支付的数额为预拍卖中获胜竞拍者提出的报价;③将代表成员向中心提交的转移支付分配给串谋组织内的所有成员(包括竞拍获胜者);④建议正式拍卖中,代表成员低于其估价出价,所有其他串谋组织的成员不参与竞价、提交零报价或者以保留价格出价;⑤对背叛组织的成员实行某种方式的惩罚。
第二阶段为预拍卖之后的正式拍卖,正式拍卖采用的是密封第一价格拍卖。拍卖方公布保留价格,所有估价高于保留价格的潜在拍卖者都会实际参与拍卖,参与拍卖的成员根据自己的估价向拍卖方密封递交报价,递交报价最高的成员赢得物品(最高价提交者有可能是串谋成员也有可能是非串谋成员),以其报价为最终成交和支付的价格。如果有两个或者更多的竞拍者具有相同的最高报价,那么他们就以相等的概率赢得该物品。
1.2 模型假设条件
基于上文对第一价格预拍“强”卡特尔串谋机制和密封第一价格正式拍卖两者的运作过程和性质的分析,下文设计的模型存在如下假设条件:
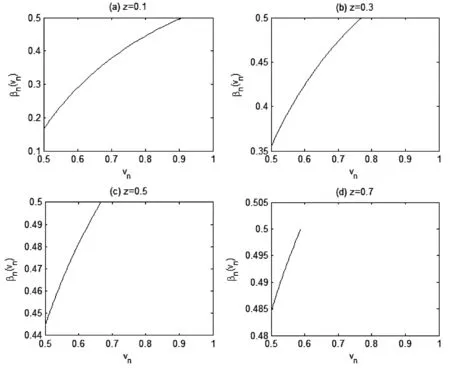
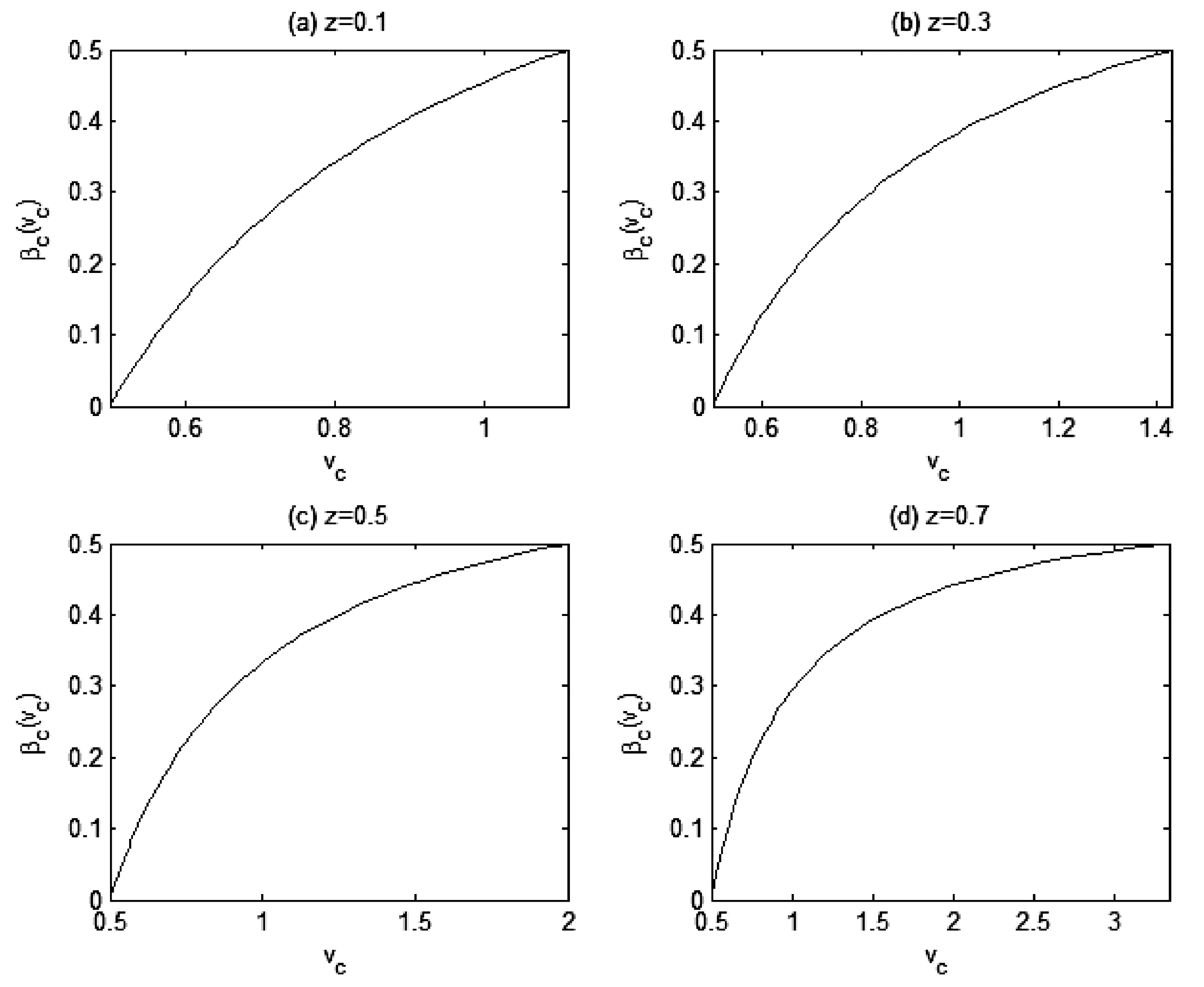
①参与正式拍卖的竞标者人数为N,其中参与价格串谋的人数为K(2≤K ②竞标者和拍卖方都是风险中性; ④暂时假设,第一价格预拍“强”卡特尔机制中存在一个均衡,其中串谋方和非串谋方分别相应地采用策略βc和βn,进一步假设βc和βn是递增的可微函数。 ⑤假定串谋组织能够采用某些惩罚措施,使得串谋成员被组织要求以不能中标的价格出价时他也不会背离串谋机制。此时,强卡特尔的第一价格预拍虽不能阻止卡特尔成员向组织撒谎,但能够引导串谋成员遵守串谋机制。 ⑥最后,也是本文的重点假设非串谋方考虑到串谋方的存在,会在出价竞标策略上进行策略性响应。 本文第二部分内容将考察,在密封第一价格正式拍卖中,串谋方和非串谋方在出价竞标策略上的互动性问题。 由于串谋组织未包含所有潜在竞标成员,因此最后中标的有可能是串谋方也有可能为非串谋方的其中之一成员。假设b1为正式拍卖中的最高出价(根据密封第一价格拍卖规则b1也为中标者的支付价格)。 (4) (5) 由(4)(5)可得 (6) (7) 化简后得: 两边同时求积分得到: 最终可得: (8) 如下图1给出N=3,K=2时非串谋方在不同z值下的最优策略βn(νn)对比。从图中可以看出随着z值得增加,串谋方和非串谋方的信息差距增大,因而对于非串谋方而言其最优策略的取值区间随z值得增加而在缩小。表明作为弱势方随着z值的增加而缩小,且下限在不断随之增大,这表明作为弱势方随着z值得增加,其在竞拍中更为弱势,为了获得竞拍,随着z值得增加其需要支付更多。 图1 N=3,K=2时非串谋方在不同z下的最优策略βn(νn)对比图 同理(7)式,根据F和G的分布可得: 对上式求一阶条件并简化,可得: 两边求积分: 可以得到关于βc(νc)和估价、正式拍卖中的出价、以及参加拍卖的人数和串谋人数的关系式: (9) 如下图2给出N=3,K=2时非串谋方在不同z值下的最优策略βc(νc)对比。从图中可以看出随着z值的增加,串谋方和非串谋方的信息差距增大,因而对于串谋方而言随着z值的增加其获得竞拍的估值下限在随之降低,即随着z值的增加,强弱之间的差距更大,作为强势方的串谋方获得竞拍的估值下限在不断降低,即对他们估值的要求在不断放宽,其可以以更低的估值来确定最优策略从而获得竞拍。 图2 N=3,K=2时串谋方在不同z值下的最优策略βc(νc)对比图 本文第三部分分析了拍卖方考虑串谋方和非串谋方在出价竞标策略的互动性从而以保留价格的变动作为策略性响应。这里沿用上文b1为正式拍卖中的最高报价(即正式拍卖中的中标者支付价格),同时为了分析方便,增加以下假设:①拍卖方对拍卖物品的估价为V0;②Y(1)和Y(2)分别表示正式拍卖中的最高和次高顺序统计量,当所有竞标者的估价都小于保留价格r,即Y(2) (1)当Y(2) ①Y(1)是非串谋方某个成员的最高顺序统计量,也就是说非串谋成员之一估价大于r,且在正式拍卖中为最高估价,其余非串谋成员的估价都小于r,同时,K个串谋成员的估价也都小于r,此种情况发生的概率为:(N-K)[1-G(r)]G(r)N-K-1F(r)k。 ②Y(1)是串谋方某个成员的最高顺序统计量,也就是说参与串谋的K个竞标者中至少有一个竞标者的估价大于r,且在正式拍卖中为最高估计,而其他N-K个非串谋成员估价都小于r,此种情况发生的概率为[1-Fk(r)]G(r)N-K。 通过对以上两种情况的分析,可得Y(2) Pr(Y(2) 那么拍卖方此时的收益为: πs=(b1-v0)Pr(Y(2) (10) (2)当r Pr(r 这种情况下,拍卖方所得到的收益为: πs=(b1-ν0)Pr(r (11) 综上,在竞拍成功情况下,拍卖方的收益为(10)+(11)即: πs=(b1-ν0)[1-FK(r)GN-K(r)] (12) 求一阶条件可得: (13) 本文研究了密封第一价格正式拍卖下的竞拍者串谋问题,且以串谋方内部实行具有转移支付的“强”卡特尔第一价格预拍机制为前提。虽然已有文章对第一价格预拍卖机制进行研究,但已有研究成果主要存在一下几点不足:(1)主要考虑卡特尔包含了所有潜在的竞拍成员情况;(2)当考虑到卡特尔没有包含所有竞拍者时,认为非串谋成员会对串谋成员做出策略性反映,但是所有竞拍者的对拍卖物品的估价是在集合{0,1}上的离散分布,而没有考虑到连续分布的情况;(3)在密封第一价格正式拍卖中,串谋方和非串谋方之间并未形成非对称的价值分布。而在事实情况中,正式拍卖中,串谋方并不总能包含所有竞拍成员,当存在非串谋方时,非串谋成员一般会考虑串谋情况的存在,形成串谋方与非串谋方之间的非对称的连续的价值分布,基于这种价值分布,在正式拍卖中,非串谋方与串谋方在竞价策略上形成互动,研究得到两个主要结论如下:(1)串谋方和非串谋方的出价策略不仅与自身的估价、竞标人数、串谋人数相关,也与对方的估价存在关联性。特别地,考虑到串谋方的存在,非串谋方在正式拍卖中出价时会隐藏自身的真实估价。(2)拍卖方的最优保留价格设定与非串谋方和串谋方的价值分布存在关联。特别地,拍卖方在面临全包含卡特尔情况下设置的最优保留价格是面临部分包含卡特尔情况下设置的最优保留价格的特例。 本文是对单期单物品的IPV的扩展研究,而在实际拍卖领域,多物品的拍卖广泛存在,同时重复拍卖中价格串谋更加稳定。所以在本文已有模型的基础上,设计针对多物品重复拍卖的价格串谋问题的防范机制是未来研究的方向所在。 [1] 祁宁,汪定伟.允许不完全拍卖的多轮逆向组合拍卖机制[J].管理科学学报,2013,16(3):61- 67. [2] 孙亚辉,冯玉强.多属性密封拍卖模型及最优投标策略[J].系统工程理论与实践,2010,30(7):1185-1189. [3] 黄河,徐鸿雁,陈剑.基于拍卖-谈判的多因素多物品采购机制设计[J].系统工程学报,2009,24(3):315-321. [4] Graham D A, Marshall R C. Collusive bidder behavior at single-object second-price and english auctions[J]. The Journal of Political Economy, 1987, 95(6): 1217-1239. [5] Graham D A, Marshall R C, Richard J F. Differential payments within a bidder coalition and the shapley value[J]. The American Economic Review, 1990, 80(3): 493-510. [6] Mailath G J, Zemsky P. Collusion in second price auctions with heterogeneous bidders[J]. Games and Economic Behavior, 1991, 3(4): 467- 486. [7] Chen C L, Tauman Y. Collusion in one-shot second-price auctions[J]. Economic Theory, 2006, 28(1): 145-172. [8] 王宏,陈宏民,等.基于第二价格预拍的竞争者合谋均衡分析[J].中国管理科学,2010,18(3):132-140 [9] Cassady R. Auctions and auctioneering[M]. University of California Pr, 1967. [10] Robinson M S. Collusion and the choice of auction[J]. The RAND Journal of Economics, 1985,16(1): 141-145. [11] Milgrom P. Auctions and bidding: a primer[J]. The Journal of Economic Perspectives, 1989, 3(3): 3-22. [12] Marshall R C, Marx L M. The vulnerability of auctions to bidder collusion[J]. The Quarterly Journal of Economics, 2009, 124(2): 883-910. [13] Porter R H, Zona J D. Detection of bid rigging in procurement auctions[J]. Journal of Political Economy, 1993: 518-538. [14] Porter R H, Zona J D. Ohio school milk markets: an analysis of bidding[R]. National Bureau of Economic Research, 1997. [15] Bajari P, Ye L. Deciding between competition and collusion[J]. Review of Economics and Statistics, 2003, 85(4): 971-989. [16] Aryal G, Gabrielli M F. Testing for collusion in asymmetric first-price auctions[J]. International Journal of Industrial Organization, 2013, 31(1): 26-35 [17] Marshall, Robert C, Leslie Marx M. The economics of collusion: cartels and bidding rings[M]. Mit Press, 2012. [18] Marshall R C, Marx L M, Meurer M J. The economics of bidder collusion[M]. Game Theory and Business Applications. Springer US, 2014: 367-397 [19] Lopomo G, Marx L M, Sun P. Bidder collusion at first-price auctions[J]. Review of Economic Design, 2011, 15(3): 177-211. [20] McAfee R P, McMillan J. Bidding rings[J]. The American Economic Review, 1992, 82(3): 579-599. [21] Marshall R C, Marx L M. Bidder collusion[J]. Journal of Economic Theory, 2007, 133(1): 374- 402. [22] 敬辉蓉,李传昭.拍卖中卡特尔的两种合谋机制研究[J].管理工程学报,2008,3(3):130-133 [21] Maskin E, Riley J. Asymmetric auctions[J]. The Review of Economic Studies, 2000, 67(3): 413- 438. Analysis of Bidder Collusion in First-Price Sealed-Bid Auction——based on “Strong” Cartel Mechanism of First-Price Pre-auction Knockout LIN Han-mi1,2, SUN Shao-rong1 (1.Business college, university of shanghai for science and technology, Shanghai 200093, China; 2.Qianjiang college, Hangzhou normal university, Hangzhou 310036, China ) The existing researches of bidder collusion in first-price sealed-bid auction have many constraints that do not conform to the reality. In view of this, by the assumption that cartels include only a partial of the bidders, collusive and non-collusive members whose value are independent,continuous and asymmetric will respond strategically to each other on bidding, this paper gets the optimal bidding price of collusive members and non-collusive members and the optimal reserve price of the auctioneer. As a result, bidding strategy of collusive and non-collusive members is not only decided by their own valuations, the numbers of bidders, the number of collusive members, but also the valuations of the other side. Optimal reserve price is related to valuation distribution of collusive and non-collusive members.Key words:first-price pre-auction knockout; “strong cartel”; bidder collusion; asymmetric distribution; reserve price 2013-12-13 国家自然科学基金资助项目(70871080,71171134);上海市教委科研创新重点项目(11ZS138);上海市哲学社会科学规划课题(2011BGL006);上海市一流学科建设项目(S1201YLXK);杭州市哲学社会科学规划课题(D14GL01) 林菡密(1981-),女,浙江奉化人,博士生;孙绍荣(1954-),男,教授,博士生导师,中国系统工程学会教育系统工程专业委员会副主任兼秘书长,研究方向:制度的工程化设计方法。 F713.359 A 1007-3221(2015)03- 0258- 08
2 串谋方和非串谋方的策略互动
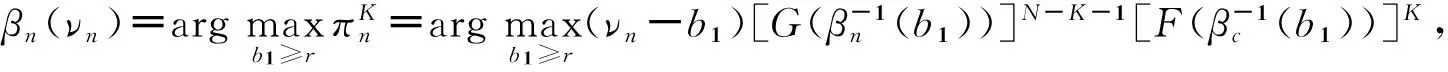
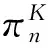
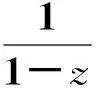
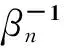
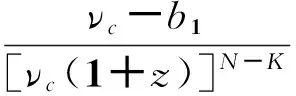
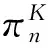
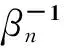
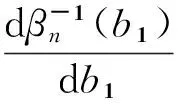
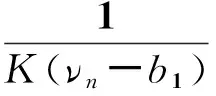
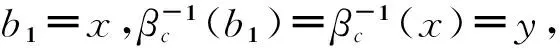
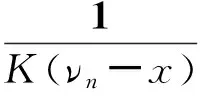
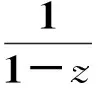
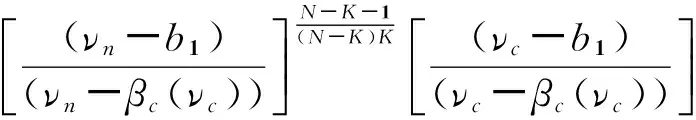
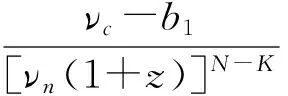
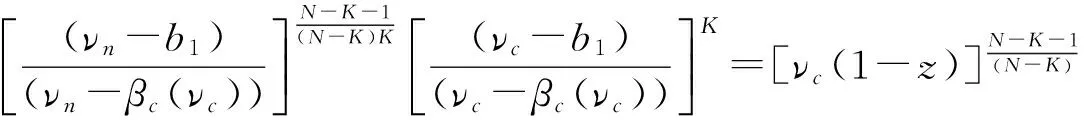
3 基于串谋方和非串谋方策略互动的拍卖方策略性响应
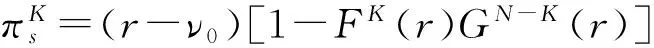
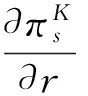
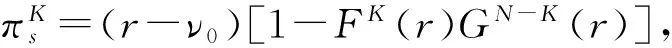
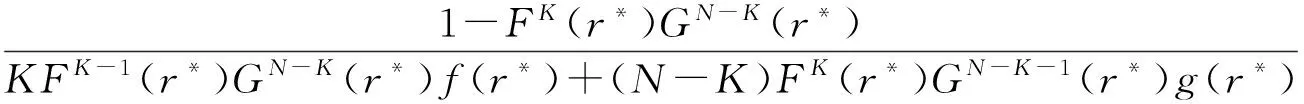
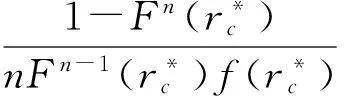
4 结论
