基于ANSYS的振荡浮子式波能发电装置主体结构的应力应变分析

宋文杰，刘 鹏，史宏达

（1.中国海洋大学 工程学院山东省海洋工程重点试验室，青岛 266100；2.山东省海洋环境监测技术重点试验室 山东省科学院海洋仪器仪表研究所，青岛 266001）

0 引言

波浪能是开发历史最悠久的海洋可再生能源，目前波浪能利用仍以波浪发电为主。波浪能发电利用型式按照技术复杂程度与开发时间大体可分为三类：振荡水柱型、聚波越浪型和机械液压型，其中机械液压型装置获能结构与波浪直接接触，通过机械或液压方式进行能量传递与转换。振荡浮子式装置属机械液压型，在欧洲被称为第三代装置，由于结构与波浪直接接触捕能，因此能量转换效率较高，可在不同水深条件（特别是超过40m的深水区）下工作[1]。

振荡浮子波能发电装置的能量转换效率较高，意味着其在大波高条件下受到破坏的可能性也非常高。目前世界各国已经提出了超过4000种波浪能转换技术，但是真正能经得起海浪考验的发电装置不多，不少装置已损坏（岸式）或沉没（船式）[2,3]。为了有效提高装置的安全稳定性与可靠性，本文将引入台风与风暴潮条件下的极限波浪条件，对发电装置的主体结构进行应力应变分析。

1 振荡浮子式波能装置模型

1.1 振荡浮子式波能装置的三维模型

本文的研究对象为振荡浮子式波浪能发电装置，为了适应恶劣海况的需求，装置设计了浮子升沉机构，当遭遇极端恶劣海况时，该机构将浮子提升至高处，脱离水面，保护其不会被破坏。该装置还设计有潮位自适应装置，使得浮子能够随着潮位的变化而保证其能够自由浮动于海面。该装置的三维模型图如图1所示。

图1 振荡浮子式波能装置的三维模型图

1.2 波浪力数学模型

根据弗汝德-克雷洛夫假定法[4]，作用在浮子上波浪为：

其中px、pz为浮子表面上任一点未受扰动入射波产生的波压强在x轴和z轴上的分量；CH、CV分别为水平绕射系数和垂直绕射系数；S为浮子浸没在流体中的总表面积；dS为浮子微元表面积。

波浪产生的波压力p可以表示为：

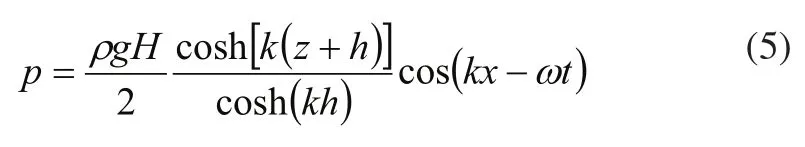
式中各物理量意义分别为：p为任一点波压力（N/m3），ρ为海水密度，g为重力加速度，h、H分别为海水水深和波高，k为波数，λ为波长，z为浮子起伏位移，ω为波浪圆频率。将上式(5)带入式(3)、式(4)进行积分，再根据绕射系数修正即可得到作用在浮体上的波浪力。

1.3 主体结构有限元模型

振荡浮子式波浪能发电装置通过浮子上下运动带动固定于其上方的液压缸运动，将波浪能转化为液压能，从而带动连接于液压缸的液压马达转动，最终通过与液压马达连接的发电机转化为电能。该装置的主体受力结构为支撑立柱，作用于立柱上的力大部分来自于通过浮子传递的波浪力，因此本文主要针对立柱和浮子进行结构强度分析，立柱与浮子的三维模型如图所示。立柱高度为9m，上下两端固定，浮子在立柱上做升沉运动。主体结构包括支撑立柱和浮子的模型如图2所示。

图2 立柱与浮子三维模型

利用Pro/E三维软件与ANSYS软件的接口，将三维模型导入到ANSYS软件中处理后进行分析。ANSYS Workbench支持壳和实体的混合装配体[5]的计算，并且能够支持边缘接触，包括实体边的接触或者是壳面的接触；根据主浮体的实际加工情况以及软件的特点，将有些接触行为定义为绑定类型，另一些定义为不分离类型[6]。

2 有限元计算结果分析

2.1 计算参数确定

本文主要考察了高、中、低三种水位情况下，波浪力作用下的立柱与浮子的应力应变特性。各工况状态参数如表1所示。有限元分析中立柱及浮子的材料选取结构钢，其弹性模量为2.06×1011Pa，泊松比为0.3，屈服强度为235MPa。

表1 各工况参数表

2.2 计算结果分析

通过建立立柱及浮子的有限元模型，并施加边界条件，计算得出各种工况条件下的应力应变情况，如图3～图5所示。

图3 高潮位时立柱与浮子的应力应变情况

图4 中潮位时立柱与浮子的应力应变情况

图5 低潮位时立柱与浮子的应力应变情况

由图3可以看出，在高潮位时，最大应力出现在立柱顶端靠近固定法兰处，最大应力值约为35.5MPa，最大位移出现在浮子与立柱的连接处，位移量约为2.8mm，最大应变出现在立柱顶端靠近固定法兰处处，最大应变值约为0.18mm。

由图4可以看出，在中潮位时，最大应力和最大应变均出现在淹没于海水中的立柱低端靠近固定法兰处，最大应力和应变值分别约为37.7MPa和0.19mm，最大位移出现在浮子与立柱的连接处，位移量约为4mm。

由图5可以看出，在低潮位时，最大应力和最大应变位置与中潮位相同，亦均出现在淹没于海水中的立柱低端靠近固定法兰处，最大应力和应变值分别约为35.3MPa和0.18mm，最大位移出现在浮子与立柱的连接处，位移量约为1.8mm。

综上可以看出，各种工况的计算结果显示立柱与浮子的应力应变均较小，高潮位时最大应力应变出现在立柱顶端，中底潮位时最大应力应变出现在立柱低端，同时浮子与立柱接触区域的应力应变区域也存在较小的应力应变，该区域的位移量最大。因此，在发电装置的设计及制造过程中，需要加强立柱与上层平台及下层潜浮体的连接，同时在浮子与立柱的连接处进行加强设计，从而保证以上区域的强度。

3 结论

目前，波浪能发电装置在海上实际应用时，如何生存是其面临的最大问题。而波浪能装置海上生存的前提条件是其主体结构具有足够高的强度，以防止在恶劣海况条件下，装置被破坏。本文通过建立主体结构的有限元模型，并加载恶劣海况下的波浪边界条件，分析了主体结构的强度可靠性，分析结果表明：在文中提到的各种海况条件下，主体结构的应力应变均较小，最大应力应变区域出现在立柱两端与上下平台的连接处，因此为了加强装置的可靠性，实际设计及制造过程中，需要加强该区域的强度，保证装置安全。

[1]Antonio F.de O.Falcao.Wave energy utilization:A review of the technologies.Renewable and Sustainable Energy Reviews,2010(14):899-918.

[2]王贵彪,李德堂,谢永和.波浪发电装置浮筒及导向柱结构强度分析[J].中国造船,2012,53(4):157-163.

[3]刘延俊,郑波,孙兴旺.漂浮式海浪发电装置主浮体结构的有限元分析[J].山东大学学报(工学版) ,2012,42(4):98-102.

[4]邱大洪.波浪理论及其在工程中的应用[M].北京海洋出版社,1985:97-99.

[5]萧凡.ANSYS软件在井架结构动态特性分析中的应用[J].山西建筑,2008,34(34):72-73.

[6]浦广益.ANSYS Workbench 12基础教程与实例详解[M].北京:中国水利水电出版社,2010.