多车型联运整车物流配送优化模型及算法研究

钱 丹，刘建胜，袁 彬，罗大海

（南昌大学 机电工程学院，南昌 330031）

0 引言

整车物流是指从汽车在制造厂完成组装下线后开始，直到送达用户手中为止的一系列仓储、运输、维护、检验、加工以及其他各种增值服务过程，是实物流、信息流、资金流的统一[1]。整车物流属于一般商品物流范畴，目前对普通商品物流的研究比较多，如徐天亮等充分考虑车辆的载重能力及其容积.在建立货物配装的数学模型[2]；Salani M等研究了基于时间窗约束的物流线路优化问题[3]，李莹莹采用粒子群优化方法对物流配送路径进行了研究[4]，Qingfang Ruan等以成本最低为优化目标，建立了结合配载和线路优化的混合优化方法[5]。

由于汽车商品与普通商品相比有其特殊，因此，汽车整车物流也有其自身的特点。一般商品物流优化调度问题可归结于装箱问题和线路优化问题，主要考虑承载空间及货物尺寸形状的约束，较少考虑承运车的实际运输能力约束，如自重、载重、限重以及相关的运输管理规则等。区别于一般物流，整车物流的运输能力约束相比其他约束条件凸显更为重要，已成为制约整车物流绩效重要因素，整车物流配送优化一般包括整车配载优化（Finished vehicle loading problem，FVLP）和整车路径优化（Finished vehicle routing problem，FVRP）。目前对整车物流配送优化研究不多[6]，马士华等在以整车运输能力为约束的条件下，研究了同一承运车型的汽车整车物流准时配载计划[7]；秦绪伟等建立了整车物流网络规划集成优化模型[8]；王婷等研究了基于返程带货的共同配送的线路优化问题[9]，这类研究大多是对FVLP和FVRP问题独立进行研究。但是FVLP和FVRP两者之间是相互影响、相互制约，FVRP优化是以FVLP的结果为输入，而FVLP装载顺序又必须考虑FVRP规划的客户群先后到达顺序，否则带来装卸的不便。因此，将FVLP和FVRP联合优化更符合物流管理实际需求，然而较少对FVLP和FVRP统一研究的。在张磊建立的整车配载和运输路线优化模型中[10]，未对空间尺寸约束加以具体考虑。因此论文以FVLP和FVRP的集成研究为切入点，基于细化的配载空间粒度和实际运输能力等约束条件，建立贴近实际需求的整车配送优化模型，重点对整车物流配载和线路优化中的算法进行详细研究，以提高优化算法的运行效率，从而提高订单处理和执行效率，并进行仿真计算与实验。

1 配送问题的数学描述

1.1 问题描述

某物流公司装车库配有多种型号的轿运车M辆，其车辆自重、体积不完全相同，主机厂下达的客户订单N个，并且每个订单目的地不同，轿运车与订单基本信息已知，在满足不同约束条件，通过合理选择配载和运输线路，使承运车发挥最大配载价值，运输支出费用最小，企业利润最大，提升服务品质和工作效率。

1.2 数学模型

整车配载数学模型如下：

目标函数：

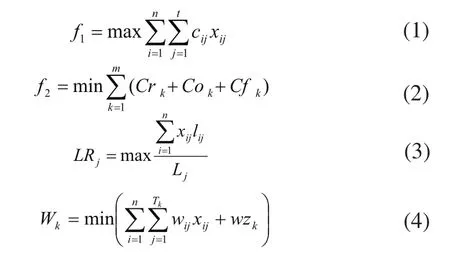
约束条件：

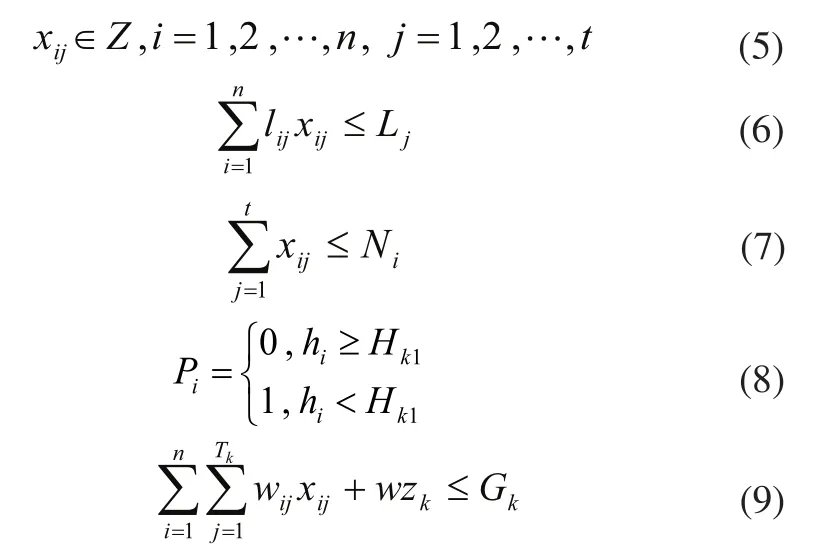
其中：m为轿运车数量，第k()辆轿运车的排数为Tk，自重为wzk，下层折算后高度为Hk1，公路承载能力的限制载重最大标准为Gk，运输中路桥费为Crk，油费为Cok，罚款费用为Cfk，轿运车的总排数为为订单数量，第i(j=1,2,…,n)订单目的地节点为di，第i订单中商品车高度为hi，总数量为Ni，第j(j=1,2,…,t)排第i种商品车的收入单价为cij，数量为xij，重量为wij，长度为lij；第j排长度为Lj。

式(1)～式(4)为目标函数，其中式(1)表示在满足配载约束条件下最大收入；式(2)表示在满足配载约束条件下最少运输支付费用；式(3)表示每辆轿运车在满足配载约束条件下最大装载率；式(4)表示每辆轿运车在满足配载约束条件下的最低总重量。式(5)～式(9)为约束条件，其中式(5)表示结果为非零正整数约束；式(6)表示轿运车每排长度约束；式(7)表示每种商品车数量约束；式(8)表示每辆轿运车下层高度约束；式(9)表示每辆轿运车最大重量约束。

2 算法设计与分析

问题的输入是包含商品车各种参数、不同交货期、不同目的地等信息的客户订单，以及装车库可用承运车运力信息，输出的是承轿运车的配载计划和线路方案。目标是订单响应时间和配载时间最短，运输支出成本最小。

针对整车配载、线路问题本身的复杂性，本文采用分层解决策略，具体思路为：基于聚类分析思想，对订单目的地节点进行分群处理，形成各个方向的客户节点单元群，再对分类后的节点信息和装车点进行线路预排序处理，结合订单中商品车信息、承运车等信息进行预配载优化，得出最后配送计划。

2.1 客户目的地聚类

随着业务不断扩展，客户点越来越多，布局越来越散乱，为提高轿运车的运载效率，借鉴数据挖掘中聚类分析思想，需对客户点进行系统聚类，形成各个方向的客户节点单元群，整体上按各中心客户群方向配送，并在MATLAB中实现此算法。

步骤1：客户节点N个，即有N个类，根据各个点之间的实际距离公里数，假设某两节点间连通有障碍，设其距离为+∞，得到距离矩阵D0；

步骤2：合并距离最近的两点归为一个新类，计算各类之间的客户节点个数；

步骤3：计算新类与当前各类的距离，若类的个数等于1，转步骤4，否则，转步骤2；

步骤4：画聚类图；

步骤5：决定类的个数，及各类包含的客户节点数。

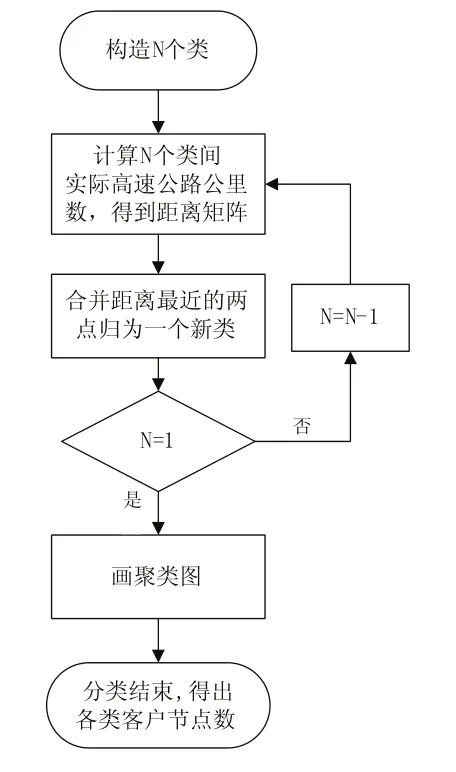
图1 客户群聚类算法流程图

2.2 启发式配载优化算法

考虑到运输规则及成本控制，订单处理应遵守完整性原则，尽量以最少的拆分，以整体进行配送。即能用一辆车完成客户的配送，不拆分至多辆承运车配送。整车配载属于复杂整数线性规划问题（ILP），常规分枝定界算法是求解ILP的有效方法。但处理较大规模问题时，常规分支定界算法分枝过于复杂，线性规划运算次数增加特别明显，迭代消耗的时间则相应大幅增加。为满足整车配载快速高效的要求，改进的分枝定界算法如下：

步骤1：先求解整数规划对应的线性规划，判断是否有解，若全为整数解，则求解结束，否则选出非整数的决策变量xi和初目标值z0；

步骤2：对每个非整数变量xi进行下取整和上取整后的线性规划，得出相应的线性规划的目标值根据优中取优准则，取最优决策目标，即取两者中较小值；

2.3 基于改进Dijkstra的车辆路径算法

在同一方向的客户节点单元群内，节点间不同的车辆行驶线路和商品车装卸，产生的运送费用也大不相同。为降低运送支出成本，基于改进Dijkstra[11]的路径算法对客户节点单元群内各节点进行排序处理，并在MATLAB中实现此算法。

步骤1：根据装车库d0与各客户节点di及各客户节点di之间的实际距离公里数假设某两节点间连通有障碍，设其距离为+∞，得到距离矩阵D1；

步骤2：取do,t(t=1,2,…,n)中最大值的节点预设为最终节点；

步骤3：调用newdijkstra函数[11]，得出线路集RS和最短总公里数，及未经节点集NS；

步骤4：判断RS集合数是否为n+1，若是，转步骤6，否则，转步骤5；

步骤5：取NS的一个节点，将其插入RS中，重新计算加入新节点的线路集RS和最短总公里数，及剩余的未经节点集NS；转步骤4；

步骤6：输出最终线路节点集。

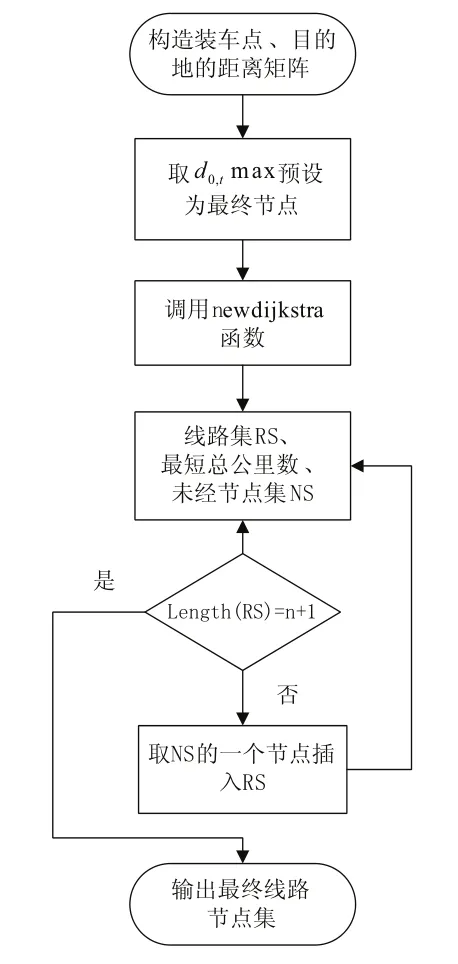
图2 车辆路径优化算法流程图

表1 订单信息表

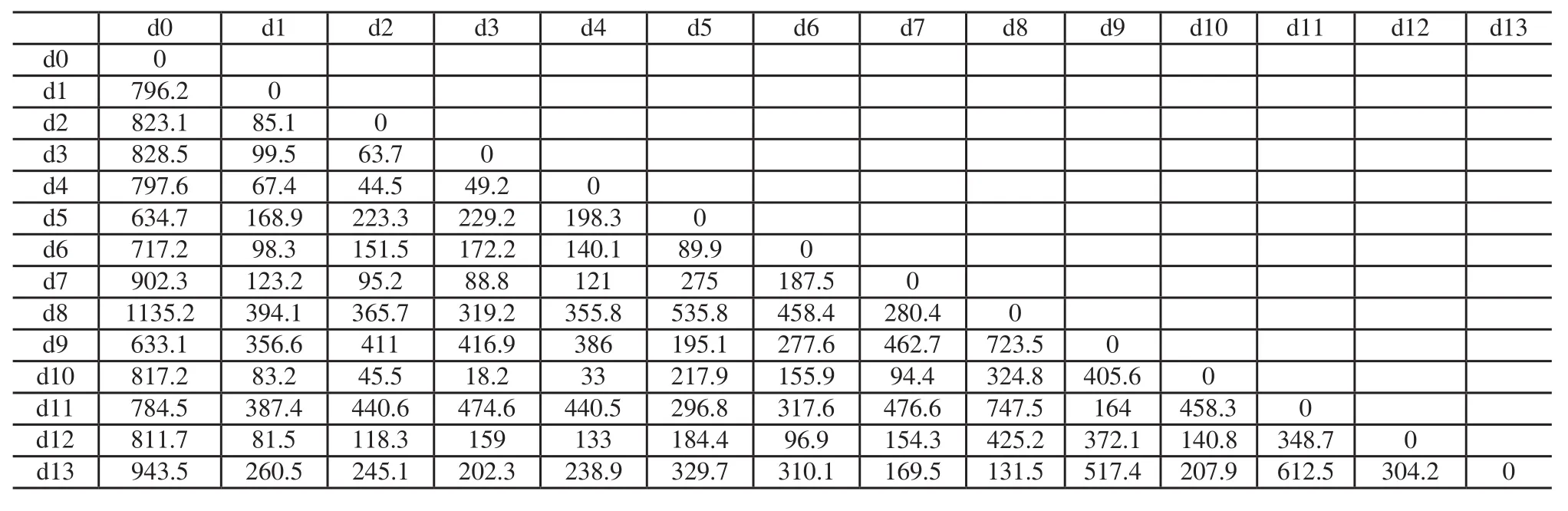
表2 客户节点距离表/km

3 数据仿真与结果分析

假设某批从装车库d0至某省13个目的地di的订单信息如表1所示。

装车库与各目的地之间高速公路距离如表2所示。

将下层曲面折算至平面后，承运车参数如表3所示。

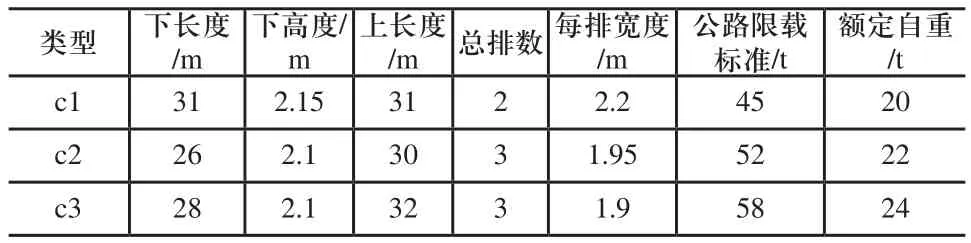
表3 承运车参数表

商品车参数如表4所示。

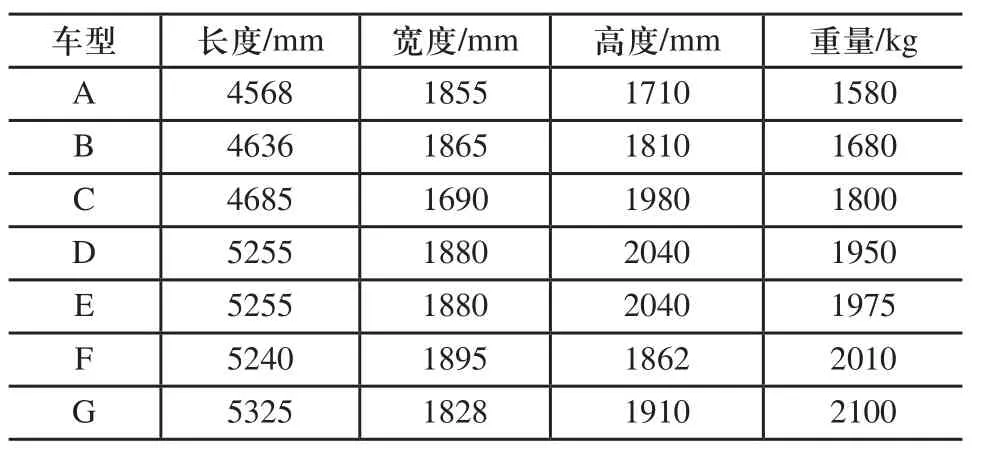
表4 商品车参数表

3.1 客户节点聚类图

根据上述订单及商品车、轿运车信息，调用客户节点的系统聚类算法对订单的客户目的地进行聚类，结果如图3所示。

3.2 配送计划表

从客户目的地聚类图中，可大致将客户目的地分为4大群，分别为：G1 = {d3，d10，d2，d4，d7，d1，d12，d6}；G2 = {d5}；G3 = {d8，d13}；G4 = {d9，d11}。将客户目的地群G1细分，得：G11={ d3，d10，d2，d4，d7} ，G12 ={d1，d12，d6}。调用启发式配载优化算法及改进Dijkstra的FVRP算法，得出需要7辆承运车进行配载，详细信息如表5所示。

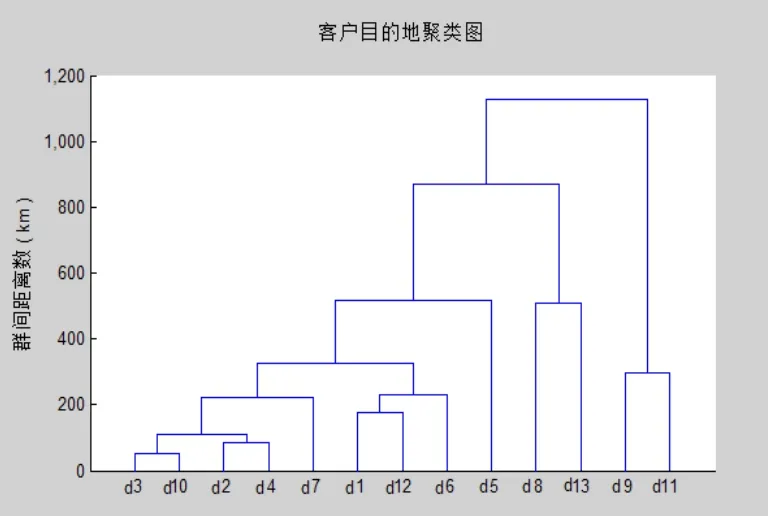
图3 客户节点聚类图

每辆承运车详细配送信息如表6所示。

3.3 结果分析

表5中每辆轿运车装载商品车数量平均，车货总重控制在高速公路限载标准之内，表6中包含了具体配载明细和配送行驶路线，从配载明细中发现，每辆轿运车尽可能将同一个目的地的客户订单及同一客户群的订单配载在一起，符合实际整车物流管理需求。

4 结论

现代汽车制造业面向订单的多品种、少批量的生产模式，直接导致了整车物流配送客户目的点多，线路分散等问题，论文运用聚类分析方法，将客户点进行聚类，形成以某客户点为核心的目的群，有效提高配载和线路规划的效率和性能。考虑实际运输能力约束条件，以最大收入和最小支出为优化目标，建立了配载优化模型，利用波动分析方法改进分支定界算法，实现配载的新启发式配送优化算法，利用改进Dijkstra算法快速优化各客户节点群内部线路优化方案，通过一系列实验分析，结果显示了模型及算法的有效性和实用性。

表5 承运车配载信息表

表6 配送详细信息表

[1]吴保峰,刘仲英.我国整车物流发展趋势及资源整合问题研究[J].汽车工程,2005,27(03):367-371.

[2]徐天亮,刘小群.多品种货物配装的优化方法[J].华中科技大学学报:自然科学版,2003,31(9):15-17.

[3]Salani M,Vacca I.Branch and price for the vehicle routing problem with discrete split deliveries and time windows[J].European Journal of Operational Research,Volume 213,Issue 3,16 September 2011:470-477.

[4]李莹莹.基于优化粒子群算法的物流配送路径问题研究[D].北京交通大学,2012.

[5]Qingfang Ruan,Zhengqian Zhang, LixinMiao, etl..A hybrid approach for the vehicle routing problem with three-dimensional loading constraints[J].Computers & Operations Research,Volume 40, Issue 6,June 2013:1579-1589.

[6]马士华,张晓龙.基于物流能力约束的整车物流计划[J].工业工程与管理,2006,(06):15-18+32.

[7]秦绪伟,范玉顺,尹朝万.整车物流网络规划问题的混合粒子群算法研究[J].系统工程理论与实践,2006(7):47-53.

[8]王婷,刘峰涛.整车汽车物流共同配送模式设计与仿真[J].计算机系统应用,2011,20(8):122-125.

[9]李军,郭耀煌.物流配送车辆优化调度理论与方法[M].北京:中国物资出版社,2001.

[10]张磊,袁建清,郑磊.汽车整车配载与运输路线优化方案及算法研究[J].计算机技术与发展,2011,21(6):219-222.

[11]袁彬,刘建胜,钱丹,等.一种基于改进Dijkstra的物流网络路径优化算法分析[J].制造业自动化,2014,(09):86-88+105.