仿人机器人冗余度双臂运动学建模与解析

罗亚梅张智军

（1.国家知识产权局专利局专利审查协作广东中心 2.中山大学信息科学与技术学院3.华南理工大学自动化学院 4.南洋理工大学媒体创新研究所）

仿人机器人冗余度双臂运动学建模与解析

罗亚梅1,2张智军3,4

（1.国家知识产权局专利局专利审查协作广东中心 2.中山大学信息科学与技术学院3.华南理工大学自动化学院 4.南洋理工大学媒体创新研究所）

针对人形机器人，提出一种融合左右臂广义逆的组合伪逆方法。该方法能将左右臂的雅克比矩阵广义逆统一为一个伪逆矩阵，从而方便使用传统伪逆方法或优化的伪逆方法处理双臂。首先给出人形机器人双臂的前向运动学模型、左右手臂的基于伪逆模型；然后将这2个单独模型的雅克比矩阵的广义逆统一到一个雅克比矩阵中，得到一个组合和简化的伪逆模型。仿真结果表明，该方案具有可行性和准确性。

人形机器人；双臂冗余度解析；组合伪逆方法；计算机仿真

0 引言

近年来，由于人形机器人与人类较相似而受到越来越多研究人员的关注[1]。人形机器人之所以受到欢迎，一方面是因为人形机器人外形与人相似，能够帮助处理一些人类需要完成的工作；另一个方面可能是人们更容易将人形机器人作为日常生活的同伴而用于家庭生活当中[2]。通过研究人形机器人，不但开发出越来越多可用于日常生活的人形机器人来满足各种需求，而且可能对人类认识本身有一定的意义。

设计人形机器人，必须考虑其运动生成方法。常见的运动生成方法为建立机器人的运动学模型，使用数学方法求解各个关节的值[3-4]。在工业机器人领域，该方法一直是研究热点，因为它具有可解释性（通过数学推理得到）、可形式化描述（使用计算机编程实现）等特点[5-6]。

冗余度机械臂是指多于完成任务所需的自由度数目的机械臂[7]。比如在三维空间中，考虑位置和姿态，若要完成末端任务，机械臂至少需要6个自由度，如果机械臂拥有7个及以上自由度，则认为这种机械臂为冗余度机械臂。相比于非冗余度机械臂，冗余度机械臂除了完成末端执行器的任务外，还有更多的优势：1) 具有更大的灵活性，由于有更多自由度，分配任务可以有更多选择；2) 可以考虑更多的优化指标，如能量最小化、力矩最小化等；3) 执行一些特殊的任务，如躲避奇异点、躲避关节极限、躲避障碍物等[8-9]。

由于有诸多优点，冗余度机械臂在近几十年越来越得到重视。冗余度机械臂的基本问题是冗余度解析问题，如果只考虑运动学，也叫逆运动学问题。具体描述为已知机械臂的末端位置，求解机械臂的各个关节值的问题。一般来说，希望能够得到运动学的解析解，即准确解。如在文献[10]中，Nunez等人给出一种针对3自由度的人形机器人运动解析方法。然而人形机器人手臂的自由度往往多于3个，所以该方法不具有普遍适用性。手臂自由度超过6个时，机械手臂往往是一个冗余型的系统，即运动学方程中方程的个数少于变量的个数，导致在求机器人逆运动学解时，难以得到唯一的解析解。为解决该问题，常用的方法是伪逆的方案[11]。

在伪逆法的使用场合中，单械臂是最常见的类型，双臂的情况比较少[3-6]。单臂系统由于只考虑单个机械臂，情况相对简单。但人形机器人往往有2个手臂，有时需各自单独完成任务，有时需协作完成任务。如搬运重物，需2个手臂具有一样的速度，且要平稳地按照既定的路线搬运；拧螺丝需一只手稳住螺丝，另一只手进行拧紧动作。因此，研究人形机器人的双臂运动学解析方法具有较大的实用价值。为了展示伪逆法在双臂解析中的有效性，本文给出一种融合左右臂广义逆的组合伪逆方法，该方法将左右臂广义逆组合为一个伪逆矩阵，从而方便使用传统伪逆方法处理双臂。

1 人形机器人双臂前向运动学建模

本文所探讨的机器人双臂具有14个自由度，即每一个手臂有7个自由度。其相应的各个子坐标系如图1所示，子坐标系{0}的原点选在其腰间的底座上，所对应的Denavit-Hartenberg参数如表1所示。

图1 双臂机器人3D模型与坐标系统

对于本文仿真使用到的机器人，参数取值如表1所示。

2 基于伪逆方法的逆运动学建模

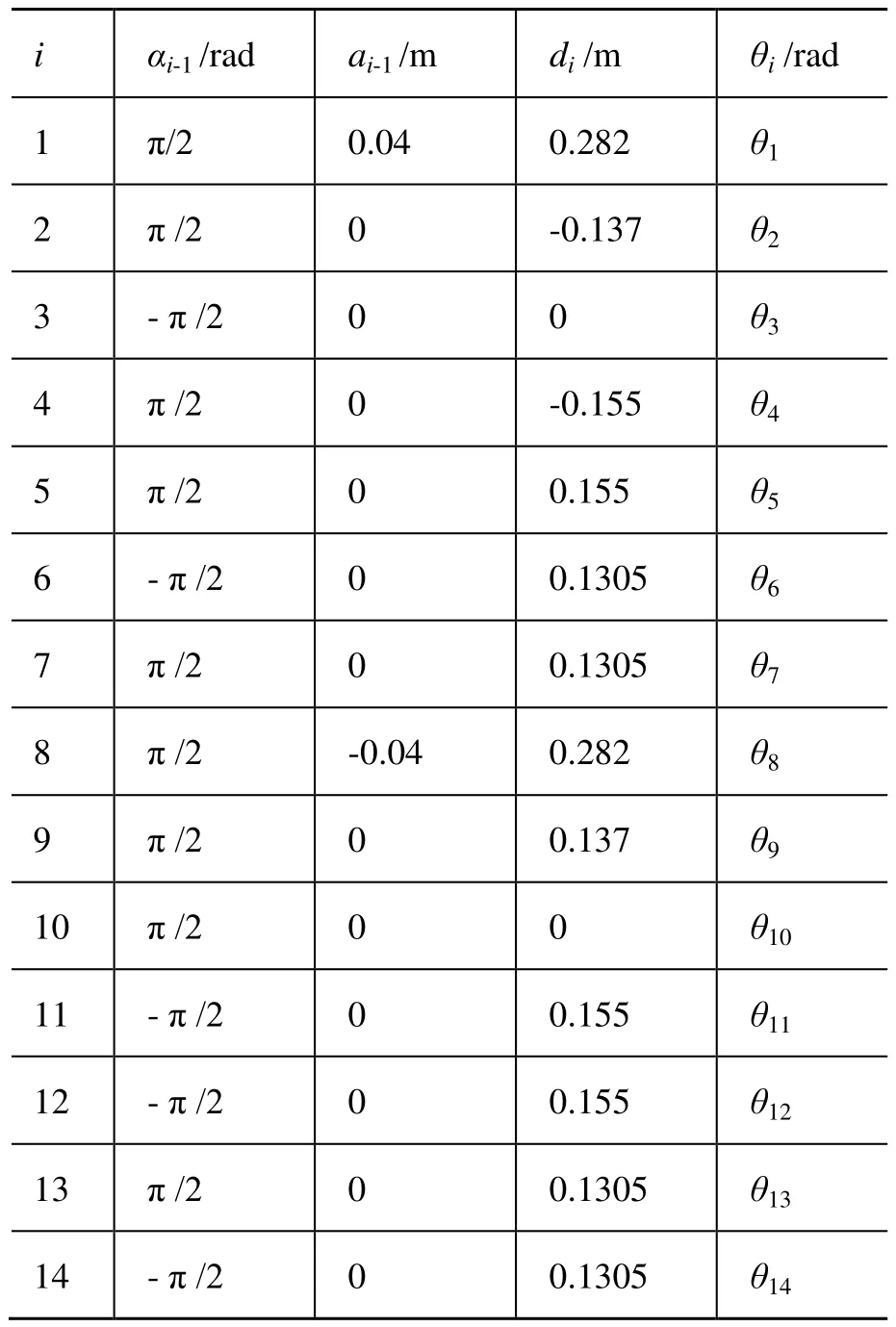
表1 双臂机器人连杆参数

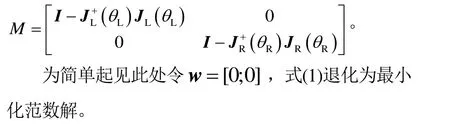
3 计算机仿真分析

为验证本文所提方案的可行性，使用上述伪逆方法控制机器人左右手分别追踪末端期望的轨迹（左手追踪一条圆形路径，右手追踪一条直线路径）。使用Matlab进行仿真，运算环境为 Precision T1600，Dell，CPU E31225 @3.10 GHz，8.00 GB RAM，64位Windows 7 Professional系统。为了实现计算机仿真，设置其初始关节角分别为

该人形机器人在追踪直线和圆形的末端期望路径时的3D运动轨迹仿真图如图2所示，机器人左右手臂分别成功追踪到了所预期的任务。任务执行过程中左右臂的关节角随着时间t变化的情况分别如图3和图4所示，任务执行过程中关节的移动过程是平滑的，没有出现震荡等情况。任务执行过程中关节速度随时间t的变化如图5和图6所示，在执行任务开始时，速度为零，中间开始具有一定的速度，到结束时速度归为零，可见此方案符合实际情况。

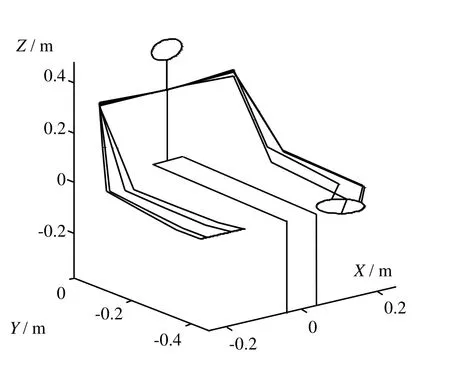
图2 使用组合伪逆方案的双臂机器人追踪圆形和直线路径的运动轨迹

图3 使用组合伪逆方案的双臂机器人左臂追踪圆形路径过程中关节角随时间的变化

图4 使用组合伪逆方案的双臂机器人右臂追踪直线路径过程中关节角随时间的变化

图5 使用组合伪逆方案的双臂机器人左臂追踪圆形路径过程中关节角速度随时间的变化

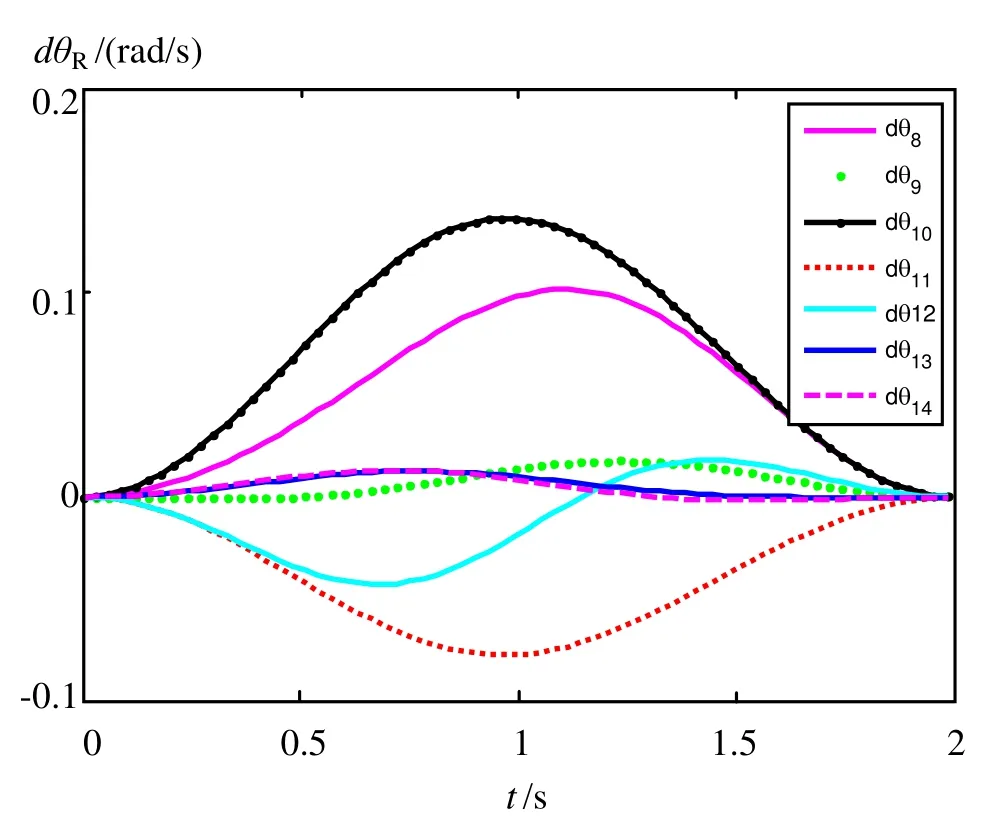
图6 使用组合伪逆方案的双臂机器人右臂追踪直线路径过程中关节角速度随时间的变化

图7 使用组合伪逆方案的双臂机器人左臂追踪圆形路径过程中定位误差

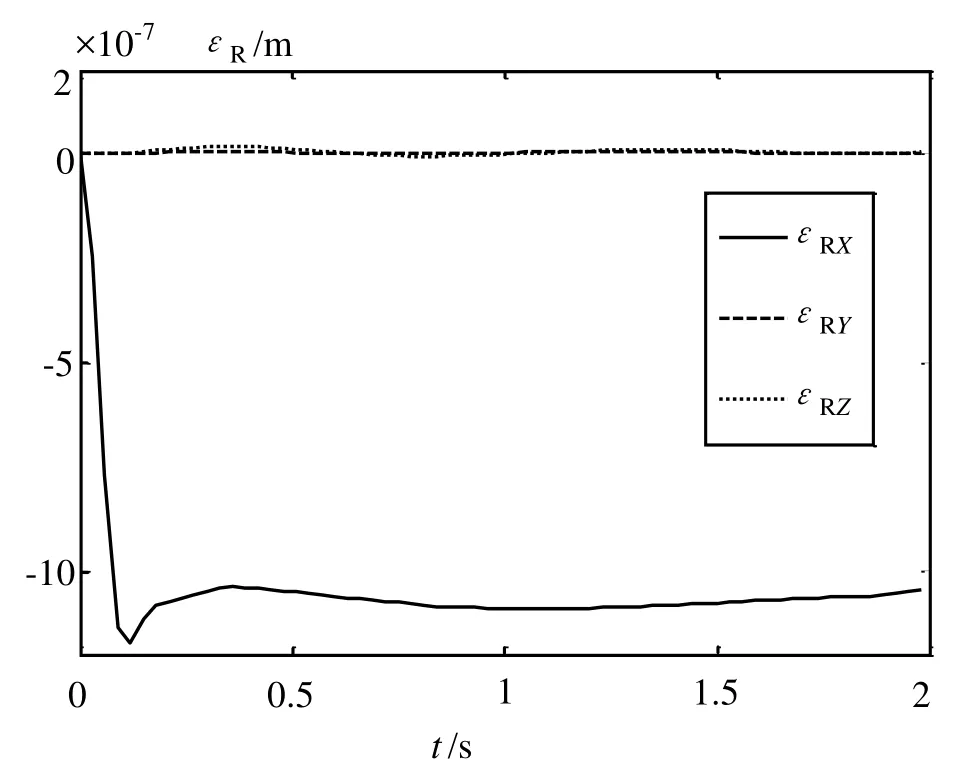
图8 使用组合伪逆方案的双臂机器人右臂追踪直线路径过程中定位误差

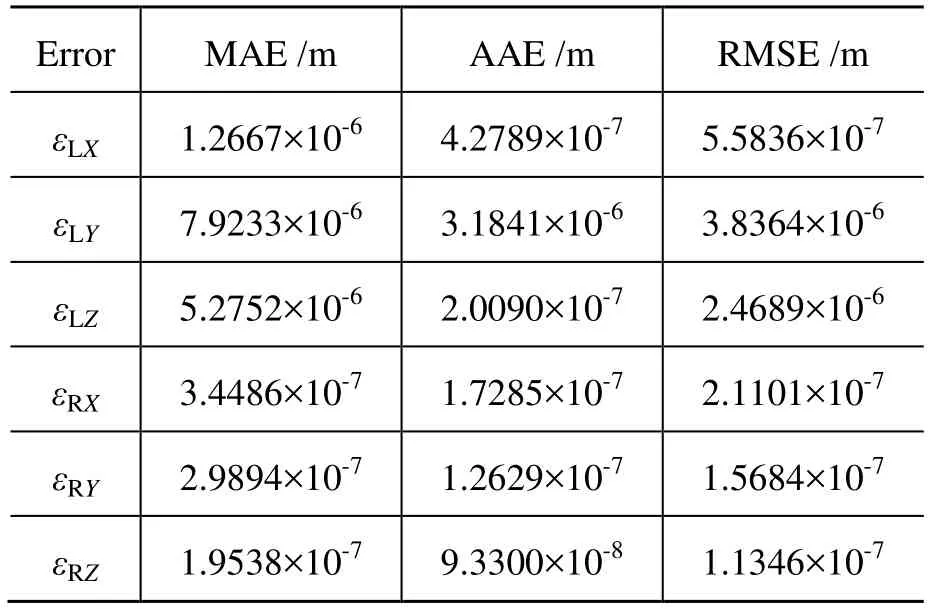
表2 基于组合伪逆法的双臂机器人完成绘制直线和圆形路径过程中产生的最大绝对值误差(MAE），平均绝对值误差(AAE)，平方根误差(RMSE)

4 结语

在一种双臂坐姿机器人的基础上，提出一种融合了左右臂广义逆的组合伪逆方法。为解析这种双臂冗余度机械臂逆运动学，首先给出这种人形机器人的前向运动学模型，再分别给出左右手臂的基于伪逆的逆运动学模型，然后将这2个单独的模型统一成一个伪逆模型处理，从而得到优化的运动学解析解。计算机仿真结果验证了这种方案的可行性和准确性。该方案目前已经被用于人-机器人的交互中，并且初步取得较为理想的效果。

[1] Lei Jie, Song Mingli, Li Zenian, et al. Whole-body humanoid robot imitation with pose similarity evaluation[J] Signal Processing, 2015, 108:136-146.

[2] Magnenat-Thalmann N, Zhang Zhijun. Social robots and virtual humans as assistive tools for improving our quality of life[C]. In 5th International Conference on Digital Home (ICDH), 2014: 1-7.

[3] Zhang Zhijun, Zhang Yunong. Acceleration-level cyclic motion generation of constrained redundant robots tracking different paths[J]. IEEE Trans. Syst., Man, Cybern., Part B, 2012,42(4):1257- 1269.

[4] Zhang Zhijun, Zhang Yunong. Variable joint-velocity limits of redundant robot manipulators handled by quadratic programming[J]. IEEE/ASME Trans. Mechatronics, 2013, 18(2): 674-686.

[5] Zhang Zhijun, Zhang Yunong. Repetitive motion planning and control on redundant robot manipulators with push-rod-type joints[J]. ASME Trans on Journal of Dynamic Systems, Measurement and Control, 2012, 135(2):1-3.

[6] Zhang Zhijun, Zhang Yunong. Equivalence of different-level schemes for repetitive motion planning of redundant robots[J]. Acta Automatica Sinica, 2013, 39(1):88-91.

[7] Zhang Zhijun, Zhang Yunong. Design and experimentation of acceleration-level drift-free (ALDF) scheme solved by two recurrent neural networks[J]. IET Control Theory & Applications, 2013, 7(1): 25-42.

[8] Yue Shigang. Redundant robot manipulators with joint and link flexibility—I. Dynamic motion planning for minimum end effector deformation[J]. Mechanism and Machine Theory,1998, 33(1): 103-113.

[9] Chyan G, Ponnambalam S. Obstacle avoidance control of redundant robots using variants of particle swarm optimization [J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(2): 147-153.

[10] Nunez J V, Briseno A, Rodriguez D A, et al. Explicit analytic solution for inverse Kinematics of bioloid humanoid robot[C]. In Robotics Symposium and Latin American Robotics Symposium, Oct. 2012: 33-38.

[11] Wang Jinguo, Li Yangmin. Inverse Kinematics analysis for the arm of a mobile humanoid robot based on the closed-loop algorithm[J]. In International Conference on Information and Automation, Jun. 2009: 516-521.

Model and Analysis of Dual-Arms Redundancy Resolution Scheme for Humanoid Robot

Luo Yamei1,2Zhang Zhijun3,4
(1. Patent Examination Cooperation Center of the Patent Office, SIPO, Guangdong
2. School of Information Science and Technology, Sun Yat-sen University
3. School of Automation Science and Engineering, South China University of Technology
4. Institute for Media Innovation, Nanyang Technological University )

A novel combined pseudoinverse method is proposed for motion generation of a humanoid robot. This combined pseudoinverse method considers both the left arm Jacob matrix and the right arm Jacob matrix. It can handle the dual-arms redundancy resolution readily. Firstly, the Kinematics equations of the left and arm rights are presented. The pseudoinverse models of the left and right arms are then presented. After that, the generalized inverse of the two separate Jacob matrixes is integrated into one Jacob matrix so that we can obtain a unified and simplified pseudoinverse model. Computer simulations and the corresponding analysis verify the effectiveness and accuracy of the proposed combined pseudoinverse method.

Humanoid Robot; Redundancy Resolution of Dual-Arms; Combined Pseudoinverse Method; Computer Simulations

罗亚梅，女，1986年生，硕士研究生，研究方向：智能机器人。

张智军，男，1982年生，博士后研究员，研究方向：智能机器人，人机交互，科学计算。E-mail: zhangzhijun@ntu.edu.sg