基于实测轨迹的高精度捷联惯导模拟器

严恭敏,WANG Jinling,周馨怡

(1.西北工业大学自动化学院,西安 710072; 2.School of Civil and Environment Engineering,University of New South Wales,Sydney,NSW 2052,Australia)

基于实测轨迹的高精度捷联惯导模拟器

严恭敏1,WANG Jinling2,周馨怡1

(1.西北工业大学自动化学院,西安 710072; 2.School of Civil and Environment Engineering,University of New South Wales,Sydney,NSW 2052,Australia)

针对传统的纯数学模型SINS惯性器件模拟器仿真效果不够逼真的问题,本文提出了一种基于已有的真实导航系统飞行记录数据的惯性器件模拟器方法。该方法利用高精度载波相位差分GNSS与中等精度IMU融合的组合导航算法,结合Kalman滤波的部分反馈修正和三次样条拟合方法,生成平滑的轨迹参数,再通过推导SINS反演算法实现了惯性器件的模拟采样仿真,反演算法中充分考虑了姿态圆锥误差和速度划船误差的补偿。通过机载飞行实验数据验证,结果表明所提惯性器件模拟器具有极高的精度性能和良好的频率特性,满足高精度SINS对数据源仿真精度和频率复杂性的要求。

GNSS;SINS模拟器;组合导航;实际飞行数据

0 引言

在惯性导航系统及其组合导航的仿真研究中,运载体的运动轨迹参数和惯性器件(陀螺和加速度计)的数据源仿真是项基础性工作,特别是研究高精度的捷联惯导系统(strapdown inertial navigation system,SINS)算法,更是需要高精度的数据模拟器作为支撑[1]。以机载SINS仿真为例,传统的基于纯数学模型的轨迹模拟器,只能给出由静止、加速、爬升、巡航和盘旋转弯等简单飞行动作组合的载机运动轨迹,运动形式过于简单,效果不够逼真,若要进一步考虑载机飞控特性和气动环境的影响,物理和数学模型往往又过于复杂,并且理想模型与实际飞行情况之间或多或少总会存在一些差距[2]。

本文基于已有的真实导航传感器飞行记录数据,利用高精度载波相位差分全球卫星导航系统(global navigation satellite system,GNSS)与中等精度惯性测量单元(inertial measurement unit, IMU)融合的组合导航算法,结合卡尔曼(Kalman)滤波的部分反馈修正和三次样条函数拟合和插值方法,生成平滑的轨迹参数,即姿态、速度和位置信息。借助传统的高精度SINS数值更新算法[3-5],推导了由姿态、速度和位置信息反向求解惯性器件增量采样输出的方法,称其为SINS反演算法,在反演算法中考虑了姿态圆锥误差和速度划船误差效应的影响,进行了相应误差的补偿。利用SINS反演算法实现了惯性器件的模拟采样输出。通过飞行实验数据验证和对比分析,惯性器件模拟采样输出具有很高的导航精度,其精度仅受限于数值算法的计算误差;惯性器件的模拟采样输出与原始真实采样输出在低频段的功率谱密度基本一致,说明了模拟采样输出能够较好地反映出载机的飞行环境特性。

1 传统的捷联惯导算法

1.1 捷联惯导系统微分方程

首先,简要说明文中涉及到的几个坐标系:惯性坐标系表示为i系,地球坐标系表示为e系,“东-北-天”导航坐标系为n系,“右-前-上”载体坐标系为b系。

SINS导航算法包含一组微分方程,即姿态微分方程、速度微分方程和位置微分方程,可分别表示为[6]

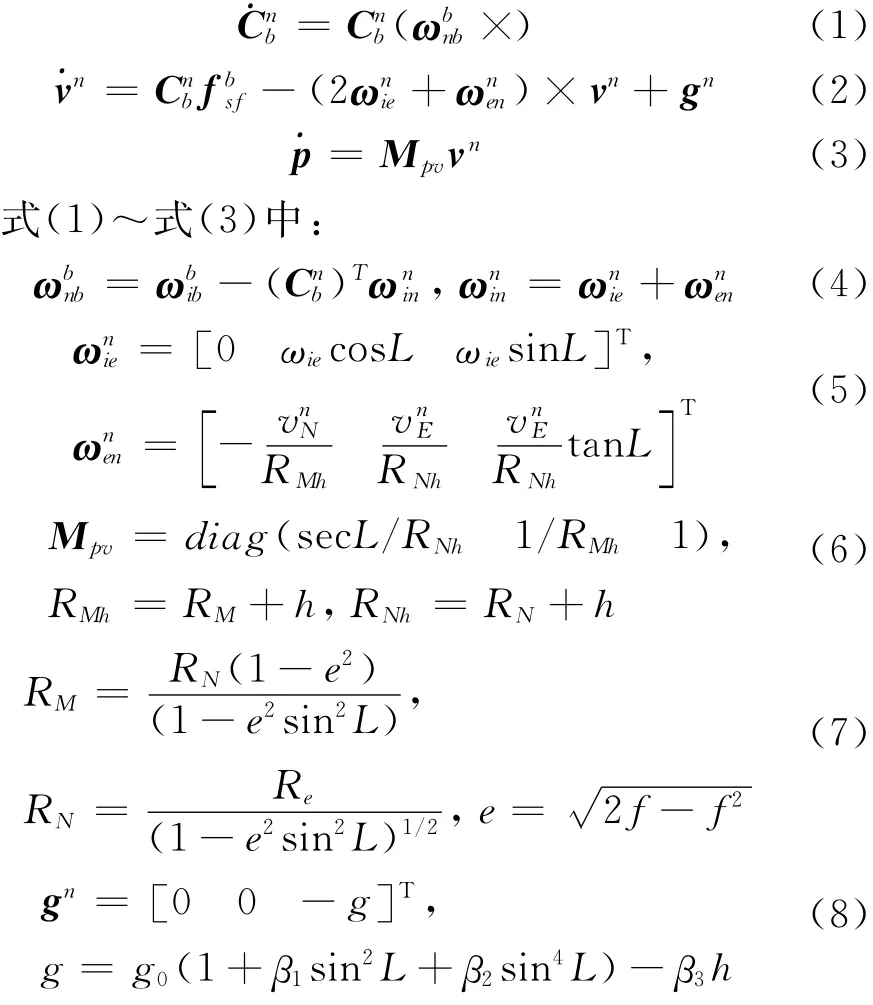
1.2 捷联惯导系统数值更新算法

SINS数值更新算法是一种航位推算算法,它根据上一时刻(tm-1时刻)的已知姿态、速度和位置导航信息,结合惯性器件在更新周期内的采样输出,递推计算当前时刻(tm时刻)的导航信息。记Tm=tm-tm-1为SINS更新周期。文中假设陀螺采样输出为角增量并且加速度计输出为速度增量,高精度的惯导系统往往都采取这种采样方式。

考虑到数值更新算法的精度和为了后续推导反演算法的方便,下面以“单子样+前一周期”误差补偿方法给出SINS数值更新算法的主体框架[3-6]。

1.2.1 姿态更新算法

下面给出由等效旋转矢量Φ计算变换矩阵C的公式

1.2.2 速度更新算法

1.2.3 位置更新算法

2 GNSS/SINS组合导航

2.1 GNSS/SINS组合Kalman滤波

采用高精度载波相位GNSS与SINS构成组合导航系统,GNSS可达厘米级的定位精度并且载机的机动大、飞行速度高,因此必需考虑到GNSS 和SINS之间的安装杆臂误差δl以及两者之间的时间不同步误差δt影响。这里建立19维的GNSS/ SINS组合Kalman滤波器,状态选取及滤波器构造为

式(18)～式(20)中各符号的含义以及详细系统参数可参见文献[6-7]。

2.2 Kalman滤波的部分反馈修正原理

为了保持惯导系统的导航误差始终为小量,即保证惯导误差方程的线性,提高滤波器模型精度,在组合导航过程中需将Kalman滤波的状态估计值不断反馈给惯导系统,进行惯导修正。传统的反馈方法是:选定某些状态参与反馈,将Kalman滤波器中的这些状态的估计值一次性全部反馈给惯导系统,修正惯导参数,再将滤波器中所有参与反馈的状态清零。但是,上述全反馈方法容易造成惯导导航输出剧烈的锯齿状波动,从而影响后续SINS反演算法的效果,在惯性器件模拟器上产生很大的间歇性脉冲失真。为了避免全反馈的不良影响,下面提出部分反馈修正原理,以经度误差的状态反馈修正为例,表示为

虽然GNSS/SINS组合导航的量测更新周期一般远大于SINS更新周期,但如果选择反馈修正周期与SINS更新周期Tm一致,并利用上述部分反馈修正方法,则可得到比较平滑的导航参数输出,为惯性模拟器的反演算法提供更加逼真的参考轨迹。当然,如欲进一步提高参考轨迹参数的求解精度,还可采用双向滤波或平滑等算法[8]。

3 捷联惯导反演算法

反演算法可以看作是常规SINS数值更新算法的逆过程。在反演算法中,假设已知姿态角和位置序列,前者为角运动信息而后者为线运动信息,再通过改造常规SINS更新算法,反向求解陀螺角增量和加速度计速度增量,实现惯性器件的高精度仿真和模拟。SINS反演算法的关键技术叙述如下。

3.1 姿态和位置的三次样条函数拟合

以位置信息中的经度为例,对组合导航输出的经度序列…,λm-1,λm,λm+1,…进行分段三次样条函数拟合,假设在时间区间t∈[tm-1,tm]上的拟合三次多项式函数为

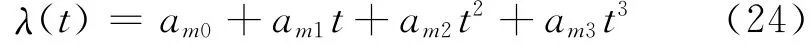
式(24)中,am0,am1,am2,am3为样条拟合系数。

经度与惯导东向速度之间的关系为

一般区间[tm-1,tm]很小,将式(25)中的L(t) 和RNh(t)取成tm-1/2时刻的值。由于位置函数已知,这里Lm-1/2可通过样条函数插值精确获得,而不象常规SINS更新算法中的那样需通过线性外推进行估计。

由式(25)移项,再将式(24)代入,即可求得东向速度函数

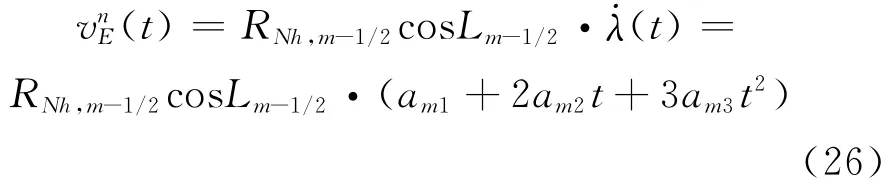
同理,对纬度和高度序列进行处理,可求得北向速度和天向速度,从而获得任意时刻的位置函数p(t)和速度函数vn(t);若对欧拉角序列进行同样处理,可获得欧拉角分段拟合函数,不妨记为A(t)。值得注意的是,如果欧拉角表示姿态存在奇异点,则需做特殊处理,这里不再详述。

随着我国教育事业的不断发展，教学模式也越来越多样化，在对人才的教育教学过程中教师应该不仅仅是进行课堂教学，通过利用数字媒体技术来提高学生的学习经验和个人素质素养。对于每个人一生的教育学习来说，专业核心能力的教育培养非常重要。加强人才培养过程中的数字媒体技术的运用，坚持社会主义教学事业的快速发展，推动科学的教育事业发展，做好对孩子德智体美的全面发展工作，做好人才的前期的培养工作，为中国未来的发展奠定有利的教育基础。

3.2 陀螺的角增量模拟

假设SINS反演算法生成惯性器件的解算周期为Tk=tk-tk-1,它可以不同于Tm,一般情况下小于Tm,Tk越小则解算精度越高。

3.3 加速度计的速度增量模拟

这里同样可假设初值Δv0=0。至此,根据式(29)和式(31)即可求解得加速度计的速度增量,完成惯性器件的模拟采样仿真。

4 实验数据处理与分析

现有一组机载导航实验数据,其SINS中陀螺的随机常值漂移约为0.03°/h,加速度计的逐次启动随机常值偏值约为200μg(特别说明:g= 9.8 m/s2,下同),原始数据输出频率200 Hz;载波相位差分GPS的定位精度为5 cm,数据输出频率1 Hz。载机飞行轨迹包括静止、滑跑起飞、转弯、巡航和在作业区域实施作业等阶段,图1给出了1 h飞行轨迹的水平投影图,其中左下角“☆”为轨迹起始点。

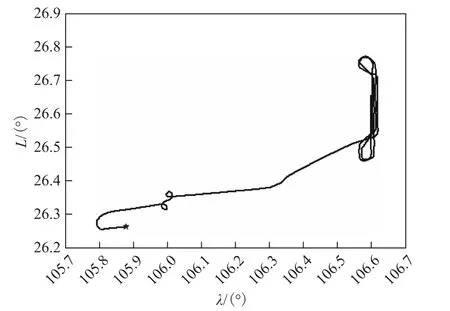
图1 飞行轨迹

对实验数据进行处理,大致过程如下:

(1)采用二子样姿态圆锥误差和速度划船误差补偿算法进行SINS导航更新,同时进行GPS/ SINS组合导航Kalman滤波,使用部分反馈修正方法修正惯导误差,这些算法均基于PSINS工具箱实现[9];

(2)对组合导航输出的100 Hz姿态和位置数据作三次样条函数拟合,获得分段连续的轨迹函数A(t)、vn(t)和p(t);

(3)对轨迹函数A(t)、vn(t)和p(t)作200 Hz等间隔插值,得到序列Ak和pk;

(4)根据SINS反演算法生成惯性器件模拟采样值Δθk和Δvk,比较IMU原始采样数据与模拟采样数据的功率谱密度(power spectrum density, PSD),参见图2,图中显示的是x轴陀螺和x轴加速度计在1 000～1 100 s的结果,其它轴和时间段的效果类似,不再给出;

(5)选用二子样误差补偿算法,由模拟采样Δθk和Δvk进行纯惯导SINS解算,但对惯导的高度通道进行了阻尼,纯惯导解算结果与(1)中的组合导航结果比较,误差参见图3。

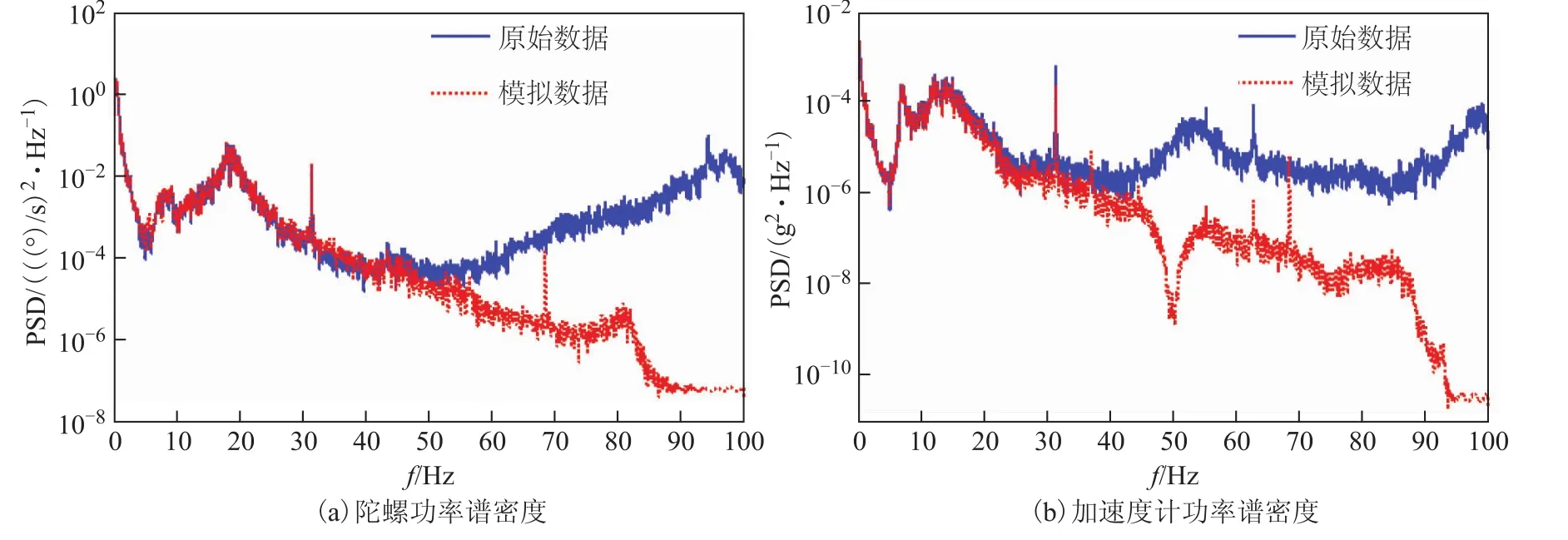
图2 原始采样数据与模拟采样数据的功率谱密度对比

图3 基于模拟采样数据的纯惯导误差

从图2可看出,原始采样数据与模拟采样数据的功率谱密度在低频段吻合得很好,说明了惯性器件模拟器能够模拟出载机的低频运动特性。图3表明,模拟采样数据具有很高的导航精度,在1 h内纯惯导的姿态误差为0.001″量级、位置误差为0.1 m量级。

5 结束语

根据传统的高精度SINS数值更新算法,它由惯性器件输出求解姿态、速度和位置等导航信息,提出了SINS反演算法,即如果已知姿态和位置轨迹信息,反向模拟求解惯性器件采样值,实现惯性器件模拟器的仿真。针对实际载机的飞行数据,需要结合GNSS进行组合导航和使用部分反馈修正技术处理,提高导航精度和获得平滑的轨迹参数,才能作为惯性器件模拟器的理想输入。实验数据处理结果表明,所提惯性模拟器具有在1 h内纯惯导位置误差0.1 m量级的精度,完全满足高精度惯导系统对数据源仿真精度的要求,如果增加模拟器求解频率,还有望进一步减少仿真计算误差;惯性器件的模拟采样数据频谱与实际采样数据频谱在低频段基本相同,如果有更高的高频一致性要求,可通过增加实际数据的采集频率或者采用单子样算法进行SINS解算来实现。

当然,在高精度的模拟器数据源之后,还可针对特定的任务需求,再加入随机漂移误差和不正交安装误差等建模误差,进行更深层次的惯性导航或组合导航仿真。

[1] HUDDLE J,GRETHEL R.Radio astro inertial Doppler error simulator[EB/OL].[2014-06-12].http://www.industrycortex.com.

[2] GPSoft.Sat Nav toolbox 3.0 for Matlab[EB/OL].[2014-06-12].http://gpsoftnav.com/products/satellite-navigation-satnav-toolbox-3-0/.

[3] PAUL G S.Strapdown inertial navigation integration algorithm design part 1:attitude algorithms[J].Journal of Guidance,Control and Dynamics,1998,21(1):19-28.

[4] PAUL G S.Strapdown inertial navigation integration algorithm design part 2:velocity and position algorithms[J].Journal of Guidance,Control and Dynamics,1998,21(2):208-221.

[5] WU Yuanxin,WANG Jinling,HU Dewen.A new technique for INS/GNSSattitude and parameter estimation using online optimization[J].IEEE Trans.on Signal Processing,2014,62(10):2642-2655.

[6] 严恭敏.车载定位定向系统研究[D].西安:西北工业大学,2006:16-27,82-84.

[7] 赵春莲.航空摄影测量中高精度POS导航算法研究[D].西安:西北工业大学,2014:60-64.

[8] 郝万亮,孙付平,崔建勇,等.双向滤波平滑在GNSS/INS组合导航中的应用[C]//中国卫星导航系统管理办公室学术交流中心.第四届中国卫星导航学术年会论文集.北京:中国卫星导航系统管理办公室,2013:1-4.

[9] 严恭敏.高精度捷联惯性导航系统Matlab工具箱[EB/OL].(2013-09-16)[2014-06-12].http://blog.sina.com.cn/s/ blog_40edfdc90101heg0.html.

High-Precision Simulator for Strapdown Inertial Navigation Systems Based on Real Dynamics

YAN Gongmin1,WANG Jinling2,ZHOU Xinyi1
(1.School of Automation,Northwestern Polytechnical University,Xi’an 710072,China; 2.School of Civil and Environment Engineering,University of New South Wales,Sydney 2052,Australia)

Traditional strapdown inertial navigation systems(SINS)simulator based on pure mathematical model cannot reflect the reality of complex dynamics of a carrier.In this paper,based on the actual flight data of an airborne navigation system,navigation algorithms of high-precision carrier phase differences global navigation satellite system(GNSS)and mediumprecision inertial measurement unit(IMU)are used,and combined with the partial feedback principle of Kalman filter and cubic spline interpolation method,to generate smooth trajectory parameters.Then,the simulation of inertial sensors is achieved with the inversed SINSalgorithm,and the new algorithm considers the impacts of attitude coning error and velocity sculling error compensation.Numerical verifications of airborne flight test have demonstrated that the inertial sensor simulator has high accuracy and good frequency characteristic,and can meet the high-accuracy SINS requirements for simulated inertial sensor data source and frequency complexity.

GNSS;SINS simulator;Integrated navigation;Actual flight data

V249.3

A

2095-4999(2015)-04-0027-05

2014-10-16

严恭敏(1977—),福建建瓯人,男,博士,副教授,主要从事惯性导航与信息融合理论研究。

注:本文于2015年5月在第六届中国卫星导航学术年会(CSNC2015)宣读过。

严恭敏,WANG Jinling,周馨怡.基于实测轨迹的高精度捷联惯导模拟器[J].导航定位学报,2015,3(4):27-31,37.YAN Gongmin, WANG Jinling,ZHOU Xinyi.High-Precision Simulator for Strapdown Inertial Navigation Systems Based on Real Dynamics[J].Journal of Navigation and Positioning,2015,3(4):27-31,37.

10.16547/j.cnki.10-1096.20150406