试题有情，讲评有意

刘烽 唐其美

试卷讲评如何充分调动学生的学习主动性和发挥试题的有效功能是目前试卷讲评课的一个难点，也是讲好试卷讲评课的一个突破点。如何利用三动课堂对试卷讲评进行再创造，本学期我从试题有情，讲评有意，主体三动进行了有益的探索。

一、分数无情，鼓励有意

以往的试卷讲评学生往往启而不发，呼而不答，学生因分数的不理想而情绪低落，课堂气氛沉闷。为扭转这种局势，首先对学生的试卷进行了分析，对现有分数的取得进行了整体认识，对预计可得分数进行了客观公正的诉求；其次，进行了适度考前考后的心理指导，帮助他们分析成功之处、失败之因；再次，通过鼓励和掌声，让学生学会正确的自我肯定与否定，从而使学生获取自信、恢复进取心，树立坚强的意志品质，消除学生心理的闭锁，提升课堂上师生的交流。

鼓励来自于四个方面：一是本次考试分数优异成绩的同学；二是此次考试与上次考试相比，有进步的同学；三是试卷整体书写优秀的同学；四是个别试题优秀解法的同学。从无情的分数中，探索出鼓励学生有意的行为。

二、思辨有情，变式有意

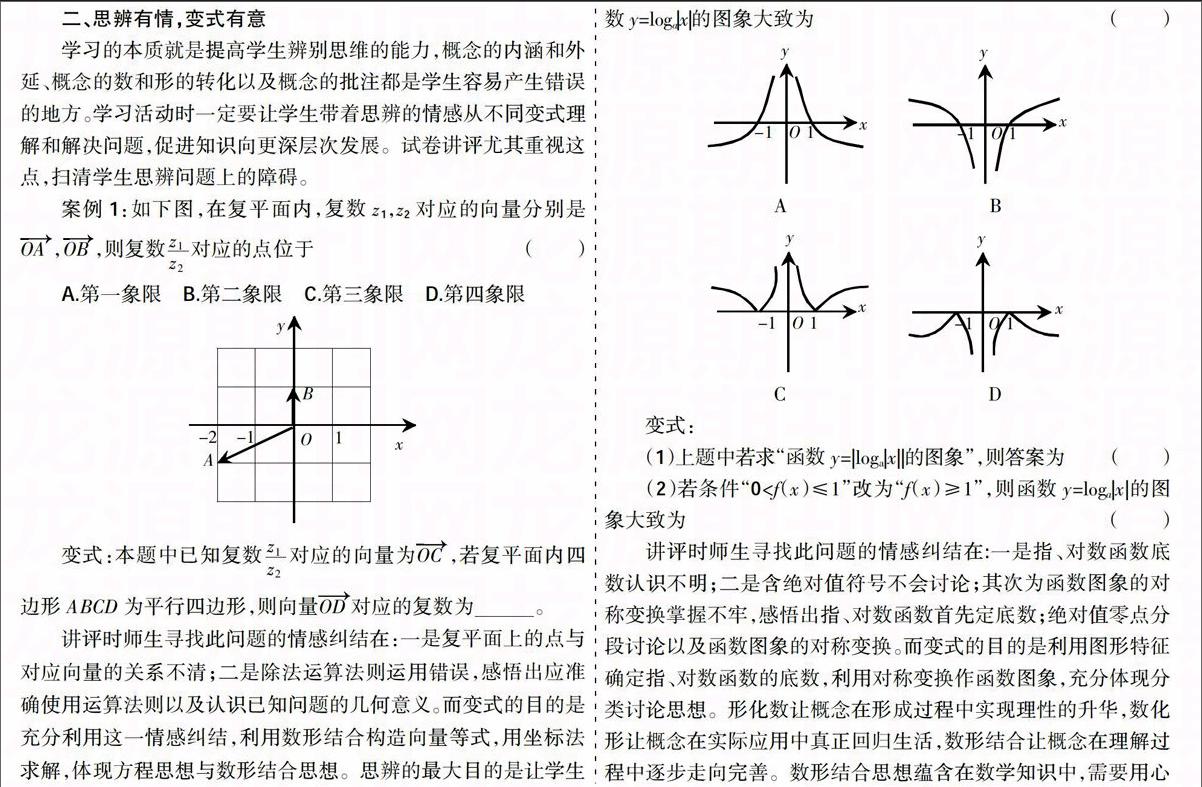
学习的本质就是提高学生辨别思维的能力，概念的内涵和外延、概念的数和形的转化以及概念的批注都是学生容易产生错误的地方。学习活动时一定要让学生带着思辨的情感从不同变式理解和解决问题，促进知识向更深层次发展。试卷讲评尤其重视这点，扫清学生思辨问题上的障碍。

讲评时师生寻找此问题的情感纠结在：一是复平面上的点与对应向量的关系不清；二是除法运算法则运用错误，感悟出应准确使用运算法则以及认识已知问题的几何意义。而变式的目的是充分利用这一情感纠结，利用数形结合构造向量等式，用坐标法求解，体现方程思想与数形结合思想。思辨的最大目的是让学生全方位认识概念，最大限度地减少因为遗漏或者忽视而产生的错误，平时一定要让学生养成对某一问题主动思辨的习惯，从正反两面来延伸知识，让思辨成为自身思考问题的情感要素之一，让变式成为思辨的有效手段之一。

三、数形有情，感悟有意

恩格斯曾说：“数学是研究现实世界的量的关系与空间形式的科学。”一般地，人们把代数称为“数”，把几何称为“形”。“数”与“形”表面看是相互独立的，其实它们的关系十分密切，在一定条件下可以相互转化，一是借助形的生动性和直观性来阐明数之间的联系，即形作为手段，数作为目的；二是借助数的精确性来阐明形的某些属性，即以数作为手段，形作为目的，实质上就是解决数学问题，将抽象的数学语言与直观的图形结合起来，使抽象思维和形象思维结合起来，实现抽象概念与具体形象的联系与转化。试卷讲评一定要挖掘试题中数与形的关系，并充分运用这一关系，让数与形这一孪生兄弟的智慧在学生头脑中充分展示，让数形情感感悟学生，感悟知识的魅力。

案例2：若当x∈R时，函数f（x）=a|x|始终满足0

变式：

（1）上题中若求“函数y=|loga|x||的图象”，则答案为（ ）

（2）若条件“0

讲评时师生寻找此问题的情感纠结在：一是指、对数函数底数认识不明；二是含绝对值符号不会讨论；其次为函数图象的对称变换掌握不牢，感悟出指、对数函数首先定底数；绝对值零点分段讨论以及函数图象的对称变换。而变式的目的是利用图形特征确定指、对数函数的底数，利用对称变换作函数图象，充分体现分类讨论思想。形化数让概念在形成过程中实现理性的升华，数化形让概念在实际应用中真正回归生活，数形结合让概念在理解过程中逐步走向完善。数形结合思想蕴含在数学知识中，需要用心挖掘，感悟使用。

四、转化有情，诱导有意

解题目的就是将陌生问题转化为熟悉问题，其实质是通过试题阅读寻找出试题中的知识和所需要求解的问题，将知识转化为方法，架设条件和结论之间的桥梁，使天堑变通途。试卷讲评时要充分调动学生的认知结构，从学生的最近思维区上来转化问题，诱导学生向有利于解题方面转化。同时要兼顾优化学生的认知结构，积极调动学生的主动性。

变式：若正数m，n满足m+n=6mn，则m+4n的最小值为 。

讲评时师生寻找此问题的情感纠结在：计算错误、不会等价转化和不会常数代换，感悟出提高运算能力和强化数学基本方法的重要性。而变式目的是利用等式以及常数与参数的交互变化，注重数学结构形式的结构转化，实质是方程思想的灵活运用。数学问题的解决离不开转化，培养学生的转化思维是学生持续发展的根本。教师在试卷讲评中应合理诱导，积极促成转化，使学生“忽如一夜春风来，千树万树梨花开”。

五、激励有情，难忘有意

学生在整个学习过程中，教师要不断鼓励学生利用已有的学习和生活经验，根据自己的思维特征，从不同角度思考问题，用不同方法解决问题，促成学生灵活思考问题的习惯。一方面对于学生呈现的多种策略要给予充分肯定，让每位学生享受成功的体验；另一方面，要鼓励学生养成回顾反思的习惯，在反思中锤炼自我，升华难忘。特别是在试卷讲评中要让学生感悟到教师的激励，教师的情感倾向，通过观察、辨析、概括、反思让学生突破难点，其精彩之处在于思路破解与优化，在评议时对学生探究过程中的迷茫加以指点，在学生遇到挫折时帮扶鼓励。

讲评时师生寻找此问题的情感纠结在：一是审题不清，二是结构形式不会等价转化，感悟出提高阅读理解能力必要性以及强化数学结构式子的数与形的等价转化，而变式目的是利用不等式以及常数与参数的交互变化，注重数学结构形式的结构转化，实质是转化与化归（构造法）思想的灵活运用。思路优化、典例剖析、反思矫正均是让学生产生难忘的关键位置，此处一定要让学生形成难忘的经历，表扬学生的一题多解，激励学生的灵光闪现，称赞学生的完美思维。

学习数学的唯一正确方法是实行再创造，也就是由学生本人把要学习的知识发现或创造出来。因此，试卷讲评不是为了讲评习题而讲，而是正确认识到该习题的功能，捕捉到了学生考试时的思维障碍，寻找到了学生考试时闪耀的思维火花，发现了试题在考试过程中学生的情感价值体验，从感情上来认识试题的本质特征，激活学生的思维来讲评，真正做到“试题有情，讲评有意”。

编辑 孙玲娟