认知诊断测验Q矩阵估计方法比较
2015-07-06涂冬波
刘 永 涂冬波
1 引言
近年来,随着认知心理学、心理测量学和计算机技术的飞速发展,认知诊断以微观认知角度对被试做出准确评估与反馈的优势在心理与教育测量领域展现出巨大发展潜力。然而,编制一份优良的认知诊断测验并非易事。正如Tatsuoka所言,认知诊断是一项复杂的工程,它至少包括“Q矩阵理论”和“诊断分类”两大部分[1]。Q矩阵是对测验项目与认知属性关系的描述,是诊断分类的基础。以往许多研究中,一般均假设所界定的测验Q矩阵是正确的,并在此基础上进行诊断分类。但是,合理界定测验Q矩阵并非易事,典型的例子就是国外许多研究者[2-9]对Tatsuoka的分数减法测验的属性界定就争论了二十多年,到目前为止仍未有定论。以至于DeCarlo曾感叹测验属性界定的复杂性,并认为它是导致目前认知诊断在实际应用中受限的主要原因之一[6,10]。研究表明错误界定的测验Q矩阵会严重影响模型参数估计及被试分类准确性[11]。因此,对高质量认知诊断测验而言,合理界定测验Q矩阵十分必要。
纵观国内外相关研究[7,10,12-14],目前界定测验Q矩阵有三种基本思路:
(1)项目的简单检查(Simple inspection of the items):该界定思路比较普遍,其主要做法是在测验Q矩阵界定之初,依据编制者自身在该领域内的经验确定项目所测属性。运用该思路Henson等人对1999年 TIMSS(Third International Mathematics and Science Study)化学测验的题目属性进行界定[13]。
(2)多评分者法(Multiple Rater Methods):该思路主要是邀请领域内若干经验丰富的专家,通过讨论或发放调查表来确定测验项目所测的属性。运用该思路界定测验Q矩阵比较广泛,比如Li等人就运用该方法对MELAB(Michigan English Language Assessment Battery)阅读测验的Q矩阵进行界定[12]。
(3)基于项目参数的迭代过程(Iterative procedures based on item parameters),该方法是在Q矩阵界定后进行模型参数估计,然后修正项目参数存在异常的项目属性,最后将修正后的Q矩阵重新纳入参数估计直到项目参数不再出现异常为止。判断项目参数是否存在异常的方法包括:MCMC估计结果是否收敛;被试属性类别的概率是否太低;拟合检验结果是否理想等[13,14]。基于这种思路de la Torre提出测验Q矩阵修正的δ法[7]、涂冬波等人提出γ法[10]。
不难发现,上述三种思路存在缺陷:第一,项目的简单检查和多评分者法采用研究者或专家意见界定测验Q矩阵虽然可以确保界定结果的可解释性,但是,不同专家知识经验间的差异及专家的遴选标准是这两种思路必须面对的问题,目前而言对这些问题的回答并没有统一的结论;第二,基于项目参数的迭代过程较前两种虽有一定客观性,但该方法往往以测验编制初期已经界定好的Q矩阵为基础,前期界定的Q矩阵的正确与否会严重影响模型的参数估计进而影响后续对Q矩阵修正的效果;第三,错误界定的Q矩阵对诊断模型拟合也比较敏感[11],一旦模型发生改变修正所得的结果往往也千差万别。
既然对高质量认知诊断测验而言合理构建Q矩阵十分必要,而上述三种界定思路又存在着诸多缺陷,那么可否存从被试作答反应入手估计出测验Q矩阵为专家界定测验Q矩阵提供参考呢?本文以Chiu[2]对Q矩阵估计方法分类为基础①Chiu(2013)按是否涉及参数估计过程将Q矩阵估计分为参数化法和非参数化法,她将数据驱动学习法归为非参数化法,但本文认为数据驱动学习法要对模型参数进行MLE估计,应属参数化法。,从参数化与否出发介绍6种基于被试作答反应的Q矩阵估计方法的思想、步骤及应用情况,总结这些方法的特点并展望未来研究方向,为认知诊断研究及应用提供借鉴和基础。
为表述方便,现对基本符号做统一规定:N、J分别为被试数和项目数;U为被试作答反应矩阵,uij为被试i对项目j的作答(1答对,0答错);K为测验考核的属性数目,qjk为项目j对属性k的考核状况(1考核,0未考核);α为被试的知识状态(Knowledge State,KS),αik为被试i对属性k的掌握状况(1掌握,0未掌握)。
2 Q矩阵非参数化估计法
非参数化估计法(Nonparametric estimation method)特点是使用统计聚类技术,以距离最短为原则确定测验Q矩阵元素,包括爬山法[15-17]和统计提纯法[2]。
2.1 爬山法(hill-climbing algorithm)② Barnes(2003,2005,2010)在其论文中称该方法为Q矩阵法(Q-matrix Method),为避免引起误解,本文以该方法所运用的爬山算法(hill-climbing algorithm)进行命名。
该法源于Tatsuoka等人提出的规则空间法(Rule Space Method,RSM)[1,18,19]。RSM认为如果由某一理想掌握模式(Ideal Mastery Pattern,IMP)对应的理想项目反应模式(Ideal Response Pattern,IRP)所确定的纯规则点与由被试作答反应向量(Response Vector,RV)确定的规则点之间距离最短,那么该IMP就为被试的属性掌握模式。爬山法沿袭这一思路,不同之处在于计算IRP上。对属性数目K已知的测验,该法具体描述如下:
(1)随机生成一个J行K列元素值在0,1之间的Q矩阵,同时生成2k个长度为K的IMP;
(2)由Q矩阵和IMP计算IRP,其第j个分量的计算公式如下:

(3)计算每个被试RV与所有IRP间的距离d,即:
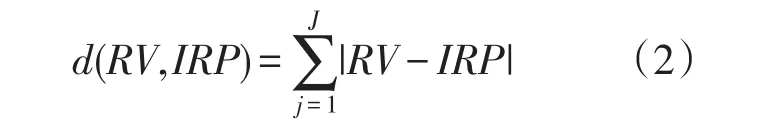
(4)将最小的d作为该被试的误差,对所有被试误差求和作为Q矩阵总误差;
(5)给单个Q矩阵元素加或减很小的值(如0.1),计算变化后Q矩阵总误差,如果总误差降低则将该元素值保存,继续下一个元素估计;
(6)重复(2)到(5)直到Q矩阵总误差小于预设值(也称终止规则)为止。
当属性数目K未知时,可依次增加属性个数直到符合终止规则①Barnes(2003,2010)认为有两种终止规则:(1)预先设定的值;(2)取Q矩阵总误差相对较小的那个Q矩阵。为止。
Barnes[15]使用该方法对北卡莱罗纳州立大学2002年秋季离散代数课程(Discrete Mathematics Course at North Carolina State University in Fall 2002)的数据进行分析,结果发现:(1)由专家定义的Q矩阵和估计的Q矩阵存在很大差异,差异主要表现在较难或较复杂项目上;(2)当项目数量较多时,估计Q的矩阵更准确;(3)如果被试作答涉及高猜测或失误,则需要大量被试,属性个数也比低猜测或低失误时要小。
该法初次尝试基于被试作答反应估计测验Q矩阵,结果虽粗糙且有不确定性,但它为后来研究提供了新思路。
2.2 统计提纯法(statistical refinement of the QMatrix)
Chiu认为基于模型的Q矩阵修正或估计的方法的缺点是当模型发生改变或模型—数据不拟合或拟合较差时,效果会大打折扣[2]。此外,随着属性、测验项目及样本量的增加,估计所耗费的时间也成倍增加。因此,Chiu提出非参数化Q矩阵估计方法——统计提纯法。
该方法认为如果某一项目的被试作答反应与理想反应间的残差平方和(Residual Sum of Squares,RSS)达到最小,就表明该项目的q向量被正确指定。具体可用下式表示:

公式3中,RSSj为所有被试在项目j的残差平方和;ηij为被试i在项目j上的理想反应(对于DINA模型,但是,现实情况下被试属性向量α一般是未知的,不能直接得到ηij,需对公式3作如下变换:
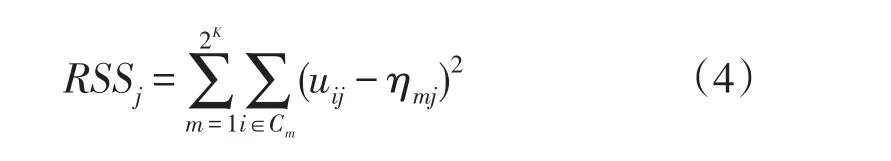
其中,Cm为第m类潜在掌握类别(Latent Proficiency-class)被试的集合;ηmj表示第m类被试对项目j的理想反应。尽管采用潜在类别m替代单个被试i,但属性分类依旧困难。Chiu(2013)指出该法以一种非参数分类法为基础,通过计算加权的Hamming距离(Weighted Hamming Distance)对被试进行分类[20]。该方法可以理解为:若属性模式αi对应的ηj能使dwh(ui,ηi)最小,那么αi就为该被试的属性掌握模式。公式表述如下:

为使该法成为可能,Chiu(2013)开发了Q矩阵提纯算法(The Q-matrix Refinement Algorithm),该算法的详细步骤如下:
(1)将S(0)={1,...,J}和Q(0)②一般而言,Q(0)为测验编制之初由专家界定的Q矩阵。分别作为搜索项目池(Item Pool)和输入Q矩阵(Input Q-matrix);
(2)基于Q(0)使用非参数分类法获取被试属性掌握模式α;
(3)使用 α 和Q(0)计算理想项目反应 η(DINA模型中
(4)使用η和观察项目反应u计算每个项目上所有被试的平均RSS(mean RSS across examinees),选择项目池S(0)中最大RSS的项目,将其q向量记为;
(7)在S(0)中删除项目j并更新为S(1);
(8)用 Q(1)和 S(1)替换 Q(0)和 S(0),重复(2)至(7)步,直到所有项目都被更新;
(9)重复(1)至(8)直到每个项目的RSS不再变化为止。
Chiu模拟考察了样本量、属性个数、被试属性分布、项目参数上限、Q矩阵错误率、误设类型及诊断模型等对该法的影响,结果发现:(1)Q矩阵平均判准率(Mean q-entry Recovery Rate,MRR)随样本量和测验长度增加而增加;(2)属性个数及项目参数上限与MRR呈反比;(3)被试属性掌握模式呈离散均匀分布(Discrete Uniform Distribution)和高阶分布(Higher Order Model)比多元正态分布(Multivariate Normal Threshold Model)的MRR要高;(4)无论何种Q矩阵错误率、误设类型及诊断模型,MRR都比较高。此外,她还对Tatsuoka分数减法的数据进行分析证实了模拟研究的结论[2]。
该方法的优势在于:(1)该方法较少受Q矩阵错误率及误设类型的影响;(2)它可以拓展到任意一种应用属性掌握模式和Q矩阵的诊断模型中,适用性比较广;(3)与参数化估计方法相比,该方法只需要少量被试(200人以上)就可以达到很好的效果,适用于中小样本的教育测验项目。但是,该法也有不足之处:(1)该方法以非参数分类为基础,由于非参数分类无法处理属性数目不确定的情况,因此属性数目不确定或错误设定会严重影响该方法的估计效果;(2)虽然不同诊断模型(如DINA和NIDA)对该方法的效果没有影响,但它不能识别诊断模型误设,必须以模型—数据拟合为前提。
3 Q矩阵参数化估计法
参数化估计法(Parametric Estimation Method)是将Q矩阵视为模型参数,用极大似然估计(Maximum Likelihood Estimation,MLE)或贝叶斯抽样确定未知Q矩阵元素。包括数据驱动学习法[21-23]、贝叶斯法、因素分析法和非线性惩罚估计法。
3.1 数据驱动学习法(Data-Driven of Q-Matrix)
研究表明错误界定的Q矩阵会导致模型资料严重失拟,进而出现属性识别错误[2,11,14,24]。因此,开发能够侦测Q矩阵误设及从作答数据获取Q矩阵的方法是值得探讨的。基于此Liu等人提出数据驱动学习法(也称Q矩阵自学习理论[21])。
Liu等人认为:若Q矩阵被正确指定,随着被试人数增加,由Q矩阵确定反应向量的分布与观察反应向量的分布趋于一致。其逻辑可以采用下式表示:
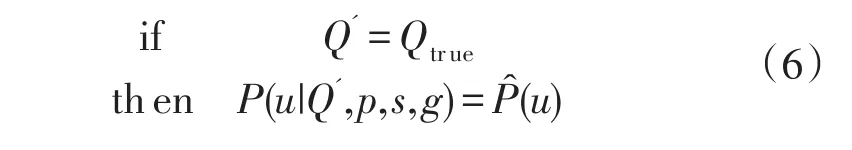
公式(6)中,Q'为待考虑Q矩阵(也可以称为Q矩阵估计值);Qtrue为Q矩阵真值;P(u|Q',p,s,g)表示由参数(Q',p,s,g)确定的反应向量u的分布;P̂(u)为作答向量u的观察分布。即:

其中,u为作答向量;Pα为P的分量,表示属性向量α在所有属性向量中的比例;ui为项目j作答;ui为被试i作答向量。
为使该逻辑具有实际意义,Liu等人引入T阵(T-matrix)的概念。T阵反映的是观察反应分布公式(8)与模型结构公式(7)间的关系,它数据驱动学习的核心。其构建过程大致如下:
(1)对于单个项目而言,令BQ',s,g(j)表示长度为2K包含P(uj=1|Q',p,s,g)有序排列的行向量,根据DINA模型,公式(7)可表示为:
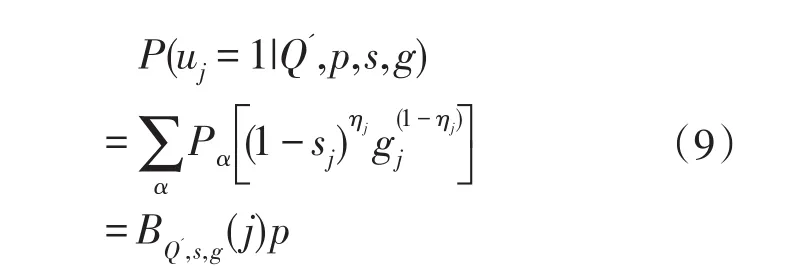
(2)就项目对(Pair of Items)而言,公式(9)可以表示为:

(3)同理,构建T阵如下:

公式(11)中的 BQ',s,g(J)与公式(1)中的 BQ',s,g(j)区别在于J表示的是多个项目的组合而非单个项目。依据公式(9),T阵可表示为:
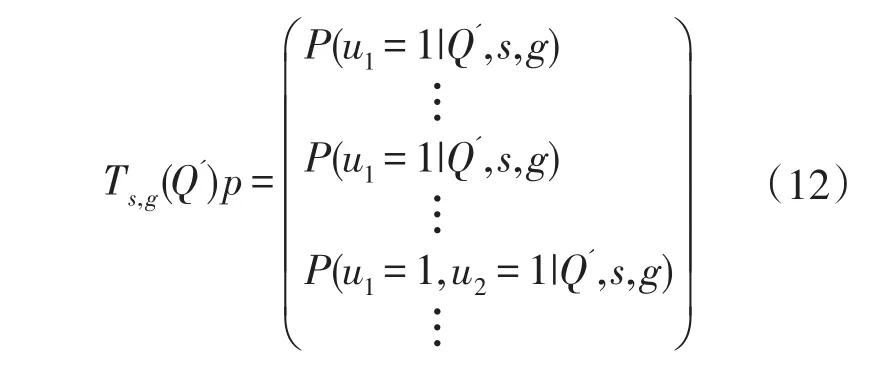
令 β为与公式(12)对应的列向量,其分量为该项目组合的人数比,即:当N→∞且β=Ts,g(Q')p时,Q'就为正确指定的Q矩阵。此时,可建立目标函数(Objective Function)如下:
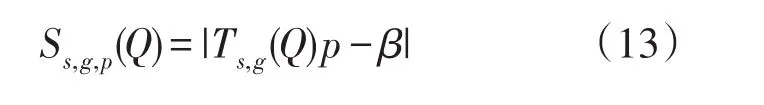
(1)确定初始Q矩阵(称为Q0),在实际应用中可用专家判断得到的Q矩阵代替。对于每个Q'而言,令Ωj(Q')为除Q'中第J行(项目)外的J×K个矩阵系列。
(2)将Q0作为迭代初值,即Q(0)=Q0。对于第m次迭代,Q0从前一次迭代Qm-1中得到;
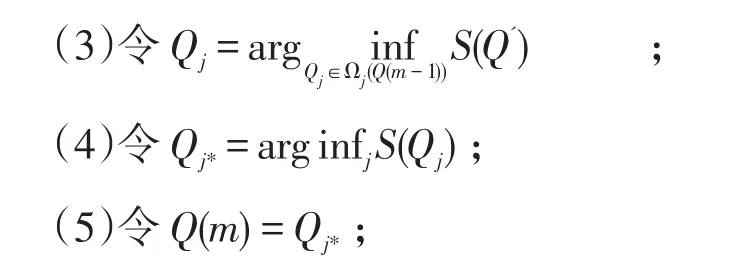
(6)重复(2)到(4)直到Q(m)=Q(m-1)。
对于每一次迭代m,算法都要更新J个项目中的一个。如果第j个项目得到更新,那么下一次迭代的Q阵就包含了项目j的属性向量,记为Qj。由于对(3)步中目标函数S的优化估计最多需要2K次,因此,每一次迭代对目标函数S的优化估计(Optimization Evaluating)需要J×2K次,这大大低于将整个Q阵进行优化所需的2J×K次。
Liu等人模拟考察样本量、属性个数、被试属性分布等因素对该方法的影响,结果发现:属性无结构、小样本(500人)且项目数固定(20题),估计Q矩阵与原始Q矩阵不一致率随属性个数增加而增加,K=5,不一致率达62%;早期终止规则①Liu等人建议设定为0.045,具体可参考Liu等人(2012)的研究。(early stopping rule)可降低小样本的高不一致率;属性α为非均匀分布(属性间存在相关),样本量影响随属性间相关程度降低而变小[22]。
样本足够多情况下应用该方法是不错的选择。但若违反“猜测参数已知”和“Q矩阵必须是完备的”①“Q阵必须是完备的”指对于无结构型的属性层级而言,测验Q矩阵必须包含单位阵。假设将导致Q矩阵无法识别,实际中能否满足还存在疑问。此外,其计算复杂度随样本量、项目和属性数目增多而变难,对大规模测验而言是不可接受的。
3.2 贝叶斯法(Bayesian extension method)
绝大多数诊断模型需要正确的测验Q矩阵,但正确界定测验Q矩阵所有元素是异常困难的。因此,Templin和Henson提出将Q矩阵若干(非全部)不确定元素视为该项目考核已知属性的主观概率,通过抽样获取这些元素的后验分布,用后验均值替代这些未知元素[24]。这是贝叶斯思想用于Q矩阵估计的雏形。
DeCarlo在Templin和Henson的基础上进行了深入研究,DeCarlo认为:允许Q矩阵某些元素是随机而不是固定的,将这些元素视为某一概率参数的Bernoulli变量,通过贝叶斯抽样来获取这些元素[4]。具体步骤如下:
(1)定义未知参数的先验分布:Q矩阵未知元素服从以Beta分布为先验分布的共轭分布(conjugate prior),即
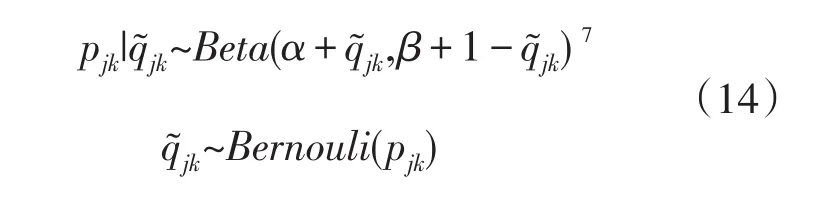
(2)由先验分布对未知元素进行抽样,得到后验分布并计算后验均值。公式如下:

(3)将后验均值作为 pjk带入(1)步得到未知元素qjk。
DeCarlo模拟考察Q矩阵元素缺失率、已知元素错误率及属性数目未知等因素对该法的影响,结果发现:估计准确率随Q矩阵元素缺失率增加而下降;估计准确率随已知元素错误率增加而降低;属性个数未知,估计准确率降低。随后,他分析Tatsuoka分数减法数据得到Q矩阵估计结果与前人研究不相上下的结论。这表明相比de la Torre的方法,该法更简便。但它在Q矩阵其他元素(非未知元素)都正确时才具有很好的效果,即它不能处理Q矩阵其他元素确定性不高或所有元素都缺失的情形。
3.3 因素分析法(Exploratory Technique)
该方法源于因素分析技术,用成分(component)表示测验涉及的技能或技能系列(skills or skill sets),通过专家对这些成分进行分析来获取Q矩阵[5]。包含两步:
(1)因素分析过程:用因素分析中主成分分析法(Principal Components Analysis,PCA)从被试作答矩阵中抽取成分矩阵和成分间相关系数矩阵;
(2)专家判断过程:邀请领域内专家对成分矩阵和成分间相关系数矩阵进行分析,得到最终Q矩阵。
为便于理解主成分分析过程,Close(2012)将DINA模型变换为符合主成分模型的形式。即:

其中,M为项目涉及的技能或技能系列数目(相当于主成分分析模型的成分数目);λjm为项目j在技能系列m的标准负荷;fim为被试i在技能系列m的标准得分。一般不能直接获取λjm和fim,需用下式得到:
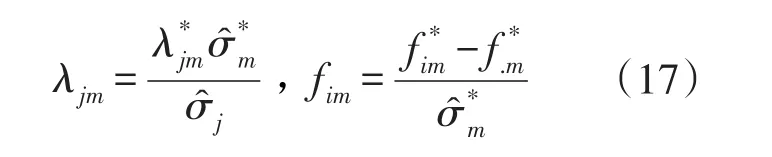

Close模拟发现:使用该法得到技能系列数目与原始Q矩阵中技能组合数目一致。随后,她以项目参数及被试分类的准确性为指标交叉验证(crossvalidation)了 Tatsuoka分数减法数据、NEAP(National Assessment of Educational Progress)2003年8年级数学测验数据和MDE(Minnesota Department of Education)2006年4年级数学测验数据,结果表明该法得到的Q矩阵无论项目参数精度还是被试分类准确性都要优于原始Q矩阵。
该方法有两个优点:第一,它可用于属性数目未知的测验,而这是其他方法达不到的;第二,计算简便,一般采用SPSS软件就可完成主成分提取。但该方法也有缺点:首先,它不适用于项目较少的测验,它要求每种技能或技能系列必须被多个项目考核,现实情况下这一前提很难得到满足;其次,它并不能直接获取Q矩阵,需专家判定才能得到,仍摆脱不了专家意见不一致及专家遴选标准不一致的困难;最后,该方法只开发出DINA模型主成分形式,在其他模型日益应用的今天略显单薄。
3.4 非线性惩罚估计法(Nonlinear Penalized Estimation)
该方法是针对Liu等人数据驱动学习法缺点提出来的。Xiang认为数据驱动学习法“Q矩阵必须是完备的”假设很难满足,当项目少而考核属性多时,它无法对Q矩阵进行准确估计[3]。此外,离散二分变量估计耗时较长,对项目较多的测验而言是不可接受的。
Xiang沿用Barnes对项目属性间关系的描述,用概率表示项目考核该属性的可能性。他认为属性掌握模式为αi的被试答对考核模式为qj项目的概率等同于该项目未考核且被试未掌握的概率见公式(19)[3,15]。具体步骤如下:
(1)令 P(uij=1|αi,qj)为属性掌握模式 αi的被试答对项目考核模式qj的概率,其公式表示如下:

(2)根据条件独立性假设,可以构建被试i在J道题上作答概率的似然为:

(3)为了使qjk∈(0,1),需要对qjk进行指数变换,用替换qjk,即:

(4)由于被试的属性向量αi无法直接获取,需要用潜在掌握模式进行替换,更具条件独立性假设,可以构建项目反应函数的似然函数如下式:
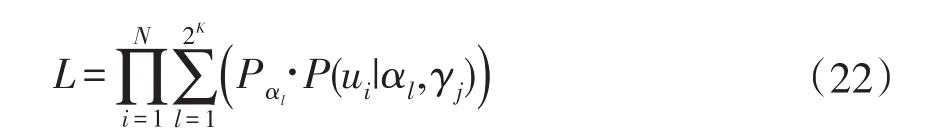
其中,P(ui|αl,γj)与公式(20)含义相同;Pαl表示属性掌握模式为αl的被试占总人数的比例。
(5)为了使结果加精确和稳健,Xiang引入惩罚函数(penalty function),具体表示如下:

上式中,λ为惩罚因子,λ越大惩罚力度越大。经Xiang验证当λ取值为9时,惩罚力度比较合适。
(6)结合公式(21)和公式(22)构建惩罚似然函数(Penalized Log-Likelihood function,LPenalized)并取对数,即:

(7)对目标函数-2log(LPenalized)进行极大似然估计(maximum likelihood estimate,MLE),得到估计Q矩阵。
(8)①如果没有专家定义的Q矩阵,该步可省略。计算专家定义Q矩阵(记为QExpert,元素为qjk)与估计Q矩阵(记为 QEstimate,元素为 q̂jk)间差异距离(discrepancy distance),通过距离最小匹配QEstimate的元素的列,即:
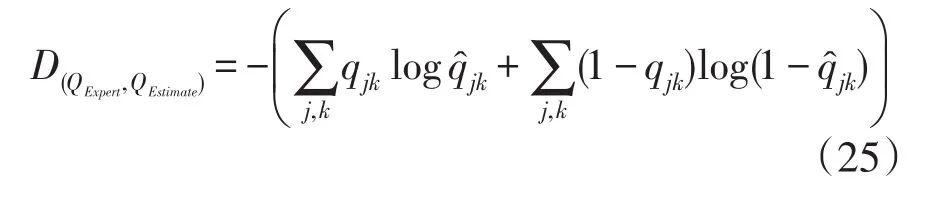
(9)以分界点(cut-off point)将估计Q矩阵离散化,得最终Q矩阵。
Xiang模拟考察了项目数量、惩罚力度和分界点对该法的影响,结果发现:判准率随项目数量增加(15题增至30题)而提高;λ取9或11,判准率最高(30题为91.3%,15题为88%);以0.5为分界点的判准率最大但误判概率也比较高。随后,他分析Tatsuoka(1990)分数减法数据发现:估计Q矩阵与de la Torre(2008)[7]界定的Q矩阵略有差异。究其原因可能与多种解题策略有关,de la Torre等人认为Tatsuoka(1990)分数减法数据存在多种解题策略[26]。
使用该法有两个明显的优势:第一,当专家无法给出合理Q矩阵或不同专家给出Q矩阵差异较大时,该方法可获取估计Q矩阵,为专家界定Q矩阵提供借鉴;第二,它可为事后修改Q矩阵提供数据支撑。但该方法也有缺陷:第一,包含较强数理分析导致步骤复杂难懂严重阻碍该方法应用;第二,λ没有固定标准,需进一步讨论分析;第三,以0.5为分界点可能导致(9)步中的Q矩阵元素出现误判现象。此外,Xiang的研究将项目参数s和g固定为0.1,而现实情境中这一条件很难得到满足。
4 小结与展望
认知诊断以结合认知心理学与心理测量学的优势在心理与教育领域展现出巨大发展潜力,但目前应用认知诊断理论编制的测验不多,其主要困难在于反映项目和属性间关系的Q矩阵无法合理界定。传统的专家评估和基于项目参数的迭代过程虽可用于界定Q矩阵但结果较粗糙,易出现专家意见不一致、专家遴选标准难确定、模型失拟和参数误差较大等问题[11,13,14]。本文从参数化与否的角度出发对现有基于被试作答反应的Q矩阵估计方法的思想、步骤及实际应用进行阐述,以期为认知诊断研究及应用提供借鉴。上述6种方法:爬山法和统计提纯法属于非参数化估计法,其他四种属于参数化估计法;爬山法、因素分析法和非线性惩罚估计法不需要提前界定Q矩阵,其他3种则需要;爬山法、因素分析法和非线性惩罚估计法可处理属性个数未知情况,其他3种则不能;爬山法和统计提纯法可用于除DINA模型外的其他诊断模型,其他4种则不能。值得注意的是:上述6种方法得到的Q矩阵并不表示完全排除专家意见,而是为专家判断提供数据支撑。下面以表格形式给本文涉及的6种Q矩阵估计方法作总体描述(见表1)。
Q矩阵是认知诊断的基础,正确界定Q矩阵对测验编制者至关重要,出于发展角度,本文对Q矩阵估计方法未来研究作以下五点展望。
第一,未来可用Monte Carlo模拟或实证综合比较各种估计方法的优劣。现有研究仅仅只是对各自提出的方法进行阐述并加以验证,鲜有对这些估计方法进行系统比较,也未有研究探讨每种方法的特点及其适用条件,这都不利于推动Q矩阵估计方法的研究。今后的研究应着重探讨如样本量、测验长度、属性个数及分布、项目参数分布、Q矩阵错误率和误设类型等因素对方法选择的影响,并开发出Q矩阵估计方法的应用软件,为实际应用者提供借鉴。

表1 Q矩阵估计方法的特点概览
第二,未来可将现有估计方法拓展到其他模型。上述6种方法只有统计提纯法和爬山法能处理除DINA模型外其他模型,而其他方法则不能。虽然DINA模型浅显易懂且估计简便,但相比其他模型(如RUM),它对被试知识状态与作答反应间关系描述相对比较简单[12,27,28]。因此,有必要将现有估计方法拓展到其他模型。此外,随着实践应用不断深入,认知诊断实践将日益关注那些多级评分项目,而上述6种方法并未涉及多级评分项目。今后研究也可将这些方法拓展到多级评分项目中。
第三,未来可结合这些方法优缺点开发新方法。如将非线性惩罚估计法不需要提前界定Q矩阵的优势与贝叶斯法准确率高的优势结合,开发一种既不需要提前界定Q矩阵又能保证高准确率的新方法。
第四,优化现有算法的运算效率。任何一种估计方法其算法的运算效率严重制约着该方法的应用范围,不论是基于参数化的方法还是基于非参数化的方法,这些估计方法都没能解决参数过多和计算耗时的问题。Chiu指出基于MLE方法的Q矩阵估计方法其面临着估计技术复杂和收效甚微的问题,反复迭代也会使计算过程耗时过长进一步限制了参数化估计方法的应用[2];相比于参数化法非参数估计法计算较为简单,但是也不能避免参数化所面临的随着属性个数的增加计算负担也将加剧的问题。因此,减轻估计方法的计算负担也应该是今后研究中应该注意的问题。
第五,未来可将这些方法应用于计算机化自适应诊断测验(cognitive diagnostic computerized adaptive testing,CD-CAT)属性标定。随着心理与教育测量理论与计算机技术的飞速发展,CD-CAT引起国内外学者的广泛关注[29-36]。与CAT一样,CD-CAT也涉及题库建问题甚至比CAT更复杂,除进行项目参数等值外还需对新题进行属性标定[33,37]。上述6种方法能否应用于CD-CAT新题属性标定呢?未来研究可着重探讨将当前Q矩阵估计方法与CDCAT属性标定相结合。
[1] Tatsuoka K K.Cognitive assessment:An introduction to the rule space method[M].Routledge,2009.
[2] Chiu C.Statistical Refinement of the Q-matrix in Cognitive Diagnosis[J].Applied Psychological Measurement,2013,37(8):598-618.
[3] Xiang R.Nonlinear penalized estimation of true Q-matrix in cognitive diagnostic models[D].Columbia University,2013.
[4] DeCarlo L T.Recognizing Uncertainty in the Q-Matrix via a Bayesian Extension of the DINA Model[J].Applied Psychological Measurement,2012,36(6):447-468.
[5] Close C N.An exploratory technique for finding the Q-matrix for the DINA model in cognitive diagnostic assessment:Combining theory with data[D].UNIVERSITY OF MINNESOTA,2012.
[6] DeCarlo L T.On the analysis of fraction subtraction data:The DINA model,classification,latent class sizes,and the Q-matrix[J].Applied Psychological Measurement,2010,35(1):8-26.
[7] de la Torre J.An Empirically Based Method of Q-Matrix Validation for the DINA Model:Development and Applications[J].Journal of Educational Measurement,2008,45(4):343.
[8] de la Torre J,Douglas J A.Higher-order latent trait models for cognitive diagnosis[J].Psychometrika,2004,69(3):333-353.
[9] Tatsuoka K K.Toward an integration of item-response theory and cognitive error diagnosis[J].Diagnostic monitoring of skill and knowledge acquisition,1990:453-488.
[10] 涂冬波,蔡艳,戴海琦.基于DINA模型的Q矩阵修正方法[J].心理学报,2012,44(4):558-568.
[11] Rupp A A,Templin J.The effects of Q-matrix misspecification on parameter estimates and classification accuracy in the DINA model[J].Educational and Psychological Measurement,2008,68(1):78-96.
[12] Li H,Suen H K.Constructing and Validating a Q-Matrix for Cognitive Diagnostic Analyses of a Reading Test[J].Educational Assessment,2013,18(1):1-25.
[13] Henson R.Q-Matrix Development[R].Annual meeting of National Council on Measurement in Education,2009.
[14] Henson R,Templin J.Q-Matrix Construction[R].Annual meeting of National Council on Measurement in Education,2007.
[15] Barnes T.Novel derivation and application of skill matrices:The q-matrix method[J].Handbook on educational data mining,2010:159-172.
[16] Barnes T.The q-matrix method:Mining student response data for knowledge[R].American Association for Artificial Intelligence,2005.
[17] Barnes T M.The q-matrix method of fault-tolerant teaching in knowledge assessment and data mining[D].North Carolina State University,2003.
[18] Birenbaum M,Kelly A E,Tatsuoka K K.Diagnosing knowledge states in algebra using the rule-space model[J].Journal for Research in Mathematics Education,1993:442-459.
[19] Tatsuoka K K.Rule space:An approach for dealing with misconceptions based on item response theory[J].Journal of Educational Measurement,1983,20(4):345-354.
[20] Chiu C,Douglas J.A nonparametric approach to cognitive diagnosis by proximity to ideal response patterns[J].Journal of Classification,2013,30(2):225-250.
[21] Liu J,Xu G,Ying Z.Theory of the self-learning Q-matrix[J].Bernoulli:official journal of the Bernoulli Society for Mathematical Statistics and Probability,2013,19(5A):1790.
[22] Liu J,Xu G,Ying Z.Data-driven learning of Q-matrix[J].Applied psychological measurement,2012,36(7):548-564.
[23] Liu J,Xu G,Ying Z.Learning Item-Attribute Relationship in QMatrix Based Diagnostic Classification Models[J].arXiv preprint arXiv:1106.0721,2011.
[24] Stout W.Skills Diagnosis Using IRT Based Continuous Latent Trait Models[J].Journal of Educational Measurement,2007,44(4):313-324.
[25] Templin J,Henson R A.A Bayesian method for incorporating uncertainty into Q-matrix estimation in skills assessment[R].Annual meeting of National Council on Measurement in Education,2006.
[26] de la Torre J,Douglas J A.Model evaluation and multiple strategies in cognitive diagnosis:An analysis of fraction subtraction data[J].Psychometrika,2008,73(4):595-624.
[27] DiBello L V,Roussos L A,Stout W.Review of cognitively diagnostic assessment and a summary of psychometric models[J].Handbook of statistics,2007,26:979-1030.
[28] Fu J,Li Y.An integrative review of cognitively diagnostic psychometric models[R].Annual meeting of National Council on Measurement in Education,2007.
[29] 骆聪,王霞,钟阳,等.CD—CAT选题策略及其应用[J].心理研究,2014,7(2):23-27.
[30] 汪文义,丁树良,宋丽红.兼顾测验效率和题库使用率的CD—CAT 选题策略[J].心理科学,2014,37(001):212-216.
[31] 骆聪,王霞,钟阳,等.CD—CAT选题策略及其应用[J].心理研究,2014,7(2):23-27.
[32] 涂冬波,蔡艳,戴海琦.认知诊断CAT选题策略及初始题选取方法[J].心理科学,2013,36(2),469-474.
[33] 陈平,张佳慧,辛涛.在线标定技术在计算机化自适应测验中的应用[J].心理科学进展,2013,21(10):1883-1892.
[34] Cheng Y.Improving cognitive diagnostic computerized adaptive testing by balancing attribute coverage:the modified maximum global discrimination index method[J].Educational and Psychological Measurement,2010,70(6):902-913.
[35] Cheng Y.When cognitive diagnosis meets computerized adaptive testing:CD-CAT[J].Psychometrika,2009,74(4):619-632.
[36] Xu X,Chang H,Douglas J.A simulation study to compare CAT strategies for cognitive diagnosis[R].Annual meeting of the American Educational Research Association,2003.
[37] 陈平.认知诊断计算机化自适应测验的项目增补:以DINA模型为例[D].北京师范大学,2011.
A Comparison of Q-matrix Estimation Method for the Cognitive Diagnosis Test
LIU Yong&TU Dongbo
