基于GARCH模型的上证180指数研究

张紫笛

摘 要：随着股票市场规模的不断扩大，股票市场的不确定性也随之加剧，为了研究股票市场的发展状况。本文选取上证180指数1996年7月4日至2015年6月18日的日收盘数据为研究对象，针对其收益率序列，运用GARCH模型、对其进行拟合和检验。结果表明，GARCH（2，2）模型能够较好的拟合上证180指数收益率序列，且具有明显的异方差性和波动性。

关键词：GARCH；收益率；上证180指数

1. 数据来源及检验分析

1.1 数据来源

本文选取上证180指数1996年7月4日至2015年6月18日的日收盘价，共4589个数据为研究对象，统计分析软件为Eviews60。

首先通过对数收益率的时序图观察收益率随时间的变动状况。对数收益率公式为：γt=lnpt-lnpt-1

式中，γt为收益率，pt为当日收盘价，pt-1为其前日收盘价。

由图1-2可知，峰度为7205571，高于正态分布的峰度值3，说明收益率序列有尖峰和厚尾的特征。拒绝上证180指数收益率序列服从正态分布的假设。

1.2 平稳性检验

由于t统计量的值小于不同显著水平下的临界值，且p值几乎为0，表明上证180指数收益率序列为平稳序列。

1.3 相关性检验

从图1-3可以看出，序列的自相关（AC）和偏自相关（PAC）系数均落入两倍标准差之内，且滞后一阶，滞后二阶和滞后三阶的Q统计量对应的P值均大于置信度005，故收益率序列在5%的显著性水平下不存在显著相关性。

2. 模型建立

通过前面的分析发现ADF检验不存在显著的相关性，因此将均值方程设定为白噪声εt。建立模型rt=πt+εt，从而整个数据的拟合效果就等同于于条件方差εt的拟合效果。

2.1 异方差性检验

有图2-1可以看出，p值均小于005，所以序列存在自相关性，因此具有ARCH效应，即收益率序列存在明显的异方差性。

2.2 GARCH模型建立

为了比较拟合程度最好的模型，本文通过比较九种常见的GARCH模型，发现只有GARCH（1，1），GARCH（1，3），GARCH（2，1），GARCH（2，2），GARCH（3，3）这五种模型的p值均小于005，也就是只有这五种模型通过了t检验。

从这九种模型的拟合结果来看，只有GARCH（1，1），GARCH（1，3），GARCH（2，1），GARCH（2，2），GARCH（3，3）这五种模型的p值均小于005，也就是只有这五种模型通过了t检验。

为了确定GARCH模型的系数，根据最小信息准则可知AIC和SC的越小模型的拟合程度越好，因此选定拟合的模型为GARCH（2，2）模型。

GARCH（2，2）的方差方程估计为：ht=115×10-7+0103575ε2t-1-0100298ε2t-2+1814103ht-1-0817697ht-2

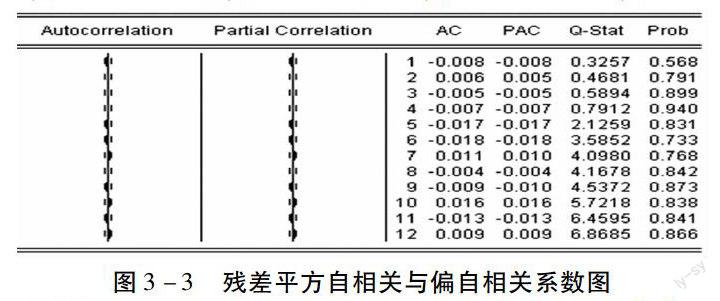
自相关和偏自相关系数近似为0，Q统计量对应的p值均大于005，因此，残差序列不再存在ARCH效应。

方差方程式中ARCH与GARCH项系数之和为0999683小于1，满足参数的约束条件。由于系数之和非常接近于1，表明条件方差所受的冲击是持久的，对所有的未来预测都有重要的作用。

3. 结果分析

（1）GARCH 模型可以适用于我国股票市场。虽然该模型是在研究发达国家的成熟金融市场过程中提出并广泛运用的，通过文章分析上证180指数的波动性条件异方差的特性较为明显，这也证明了本文应用GARCH模型反映我国股票市场收益率的波动性变化规律是正确的，并且其分析与研究结果的准确性也相对较高。（2）文章运用GARCH模型对180指数进行拟合和检验。通过对几种GARCH模型的结果比较表明GARCH（2，2）模型能够较好的拟合上证180指数收益率序列，且具有明显的异方差性和波动性。（3）收益率序列分布呈现尖峰厚尾的特点，并且存在明显的 GARCH 效应。（4）由于GARCH模型的ARCH项和GARCH项系数之和非常接近于1，表明条件方差所受的冲击是持久的，对所有的未来预测都有重要的作用。

参考文献：

[1] 陈艳，韩立磊.沪深 300 指数收益波动性实证研究[J].金融经济，2009（14）：70-72.

[2] 何红霞.中国股市价格的波动性研究——基于沪深 300 指数的 GARCH 族模型[J].和田师范专科学校学报，2010（03）：10-12.

[3] 刘璐，张倩.亚洲地区股票指数收益率的波动性研究[J].区域金融研究，2011（01）：34-39.

[4] 张彦.中国股指期货与现货的实证研究——基于沪深 300 股指期货，价值工程[J].2011（11）：126-128.

[5] 杨晨辉，刘新梅.宏观经济信息发布对沪深 300 指数波动性的影响[J].山西財经大学学报，2012（03）：38-44.

[6] 赵莉.基于GARCH模型的沪深300指数收益率波动性分析[J].四川：成都理工大学，2012.